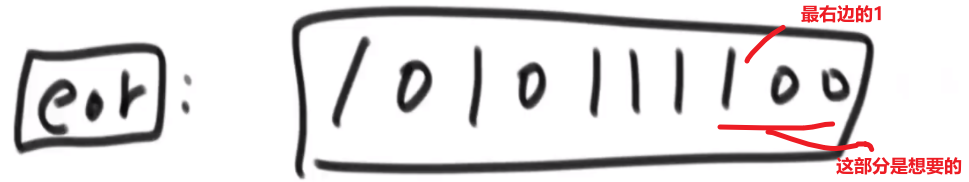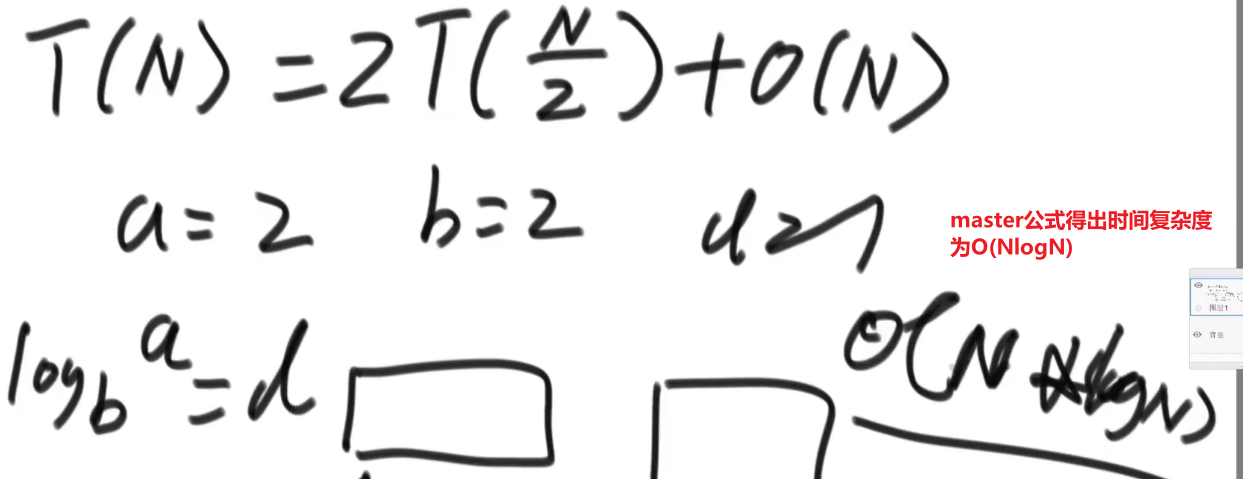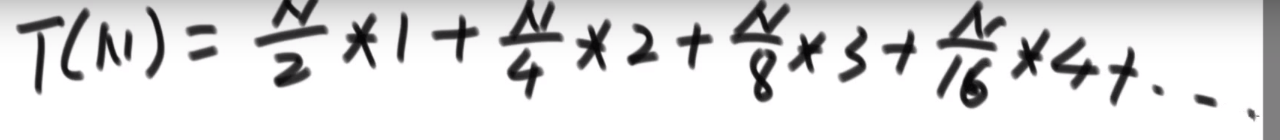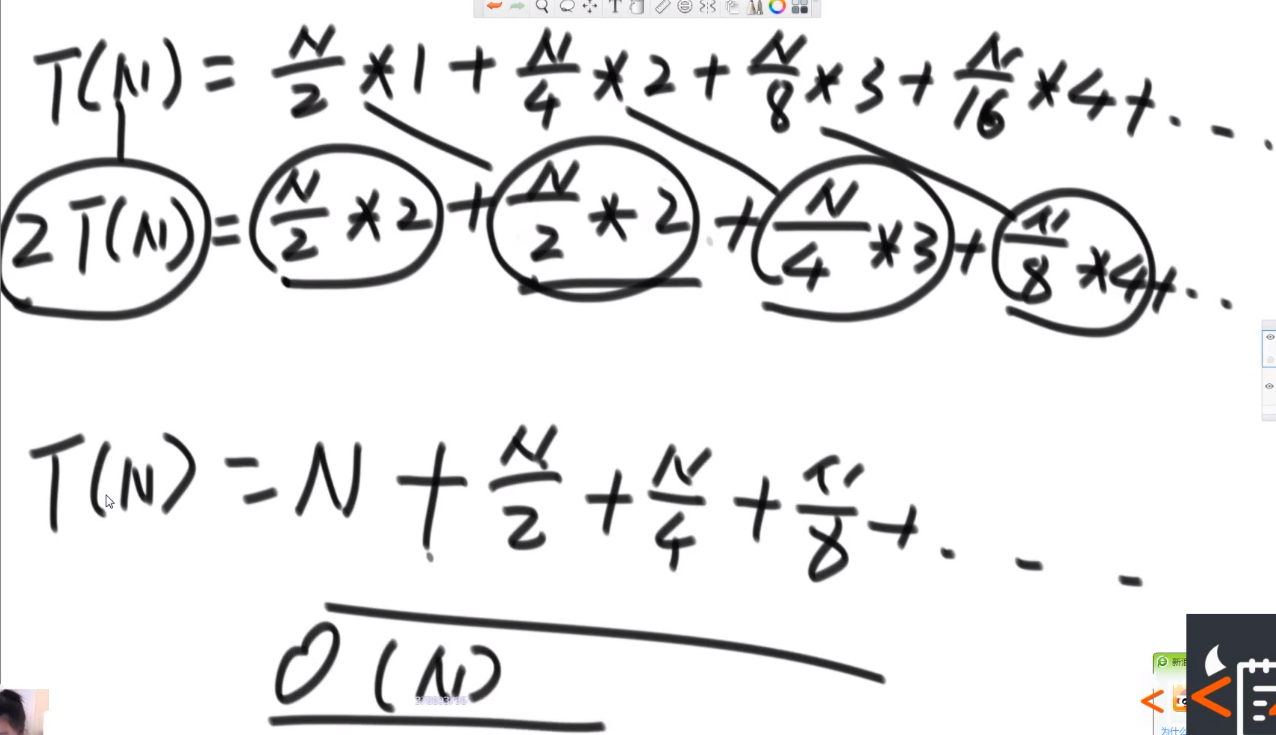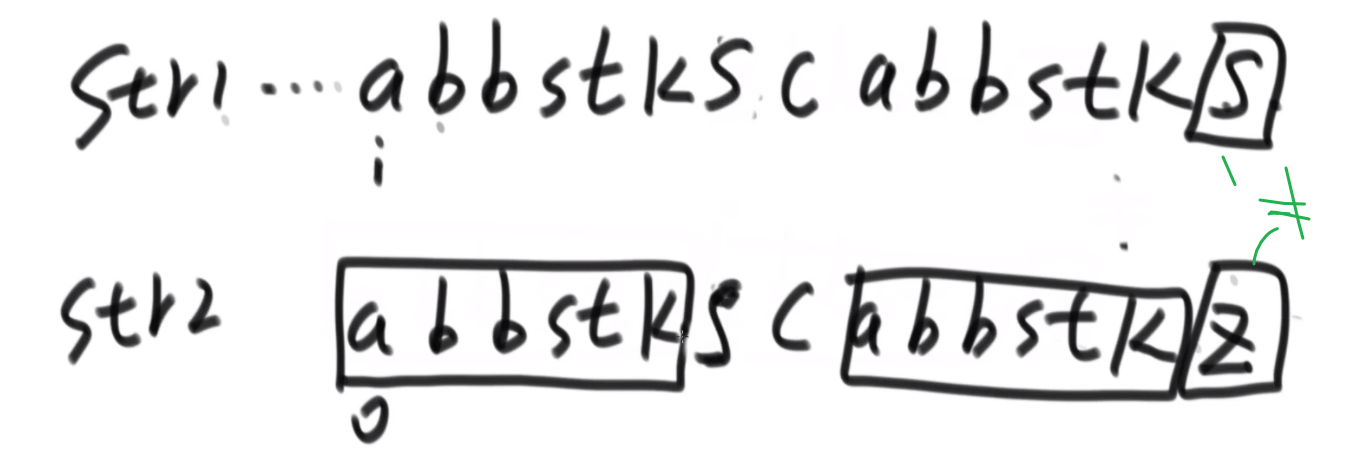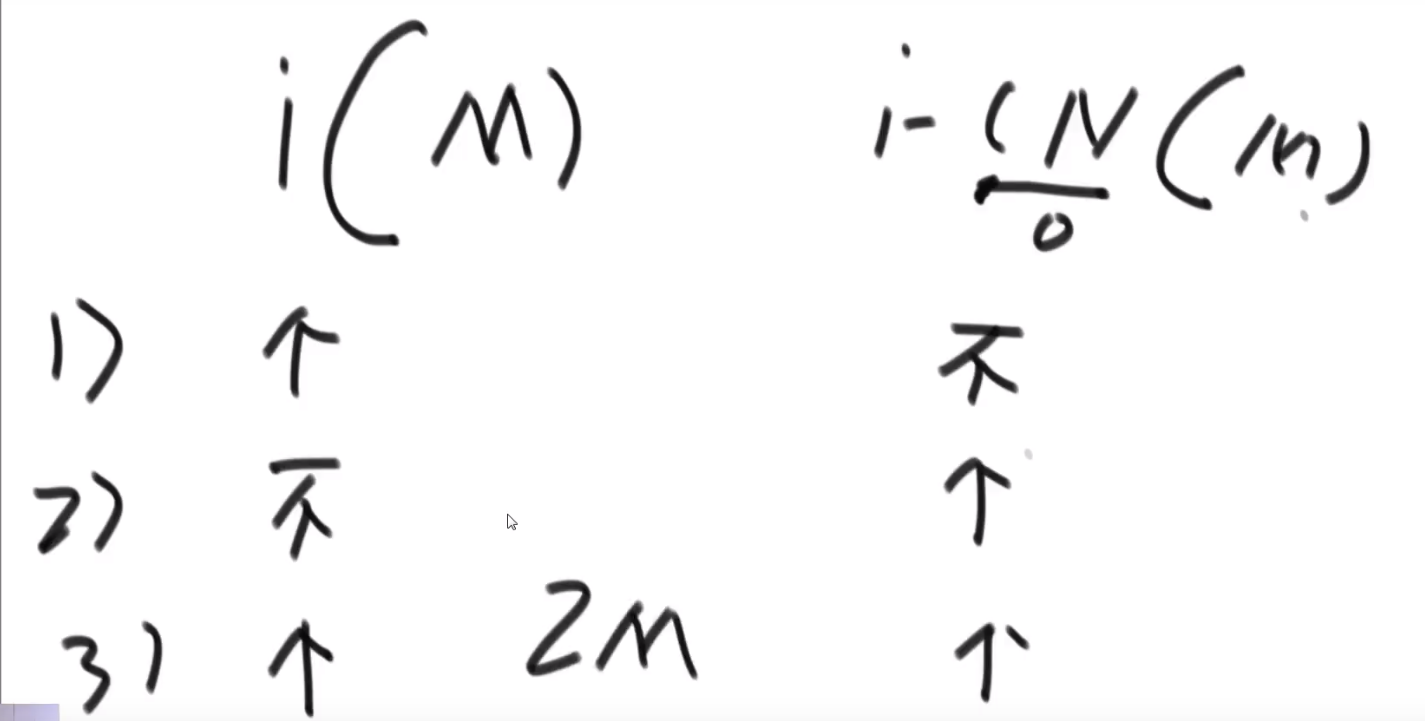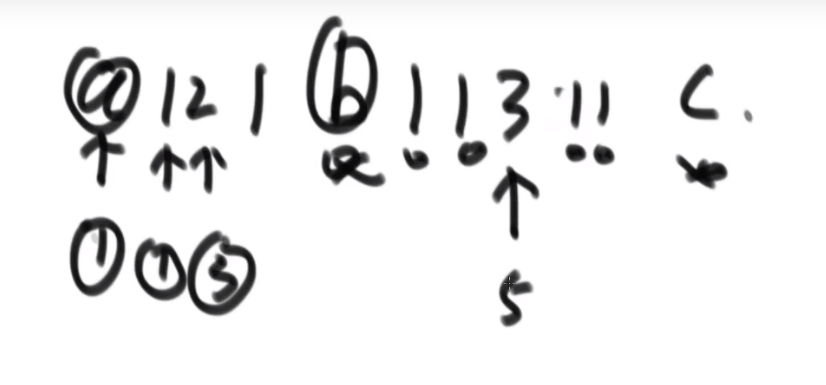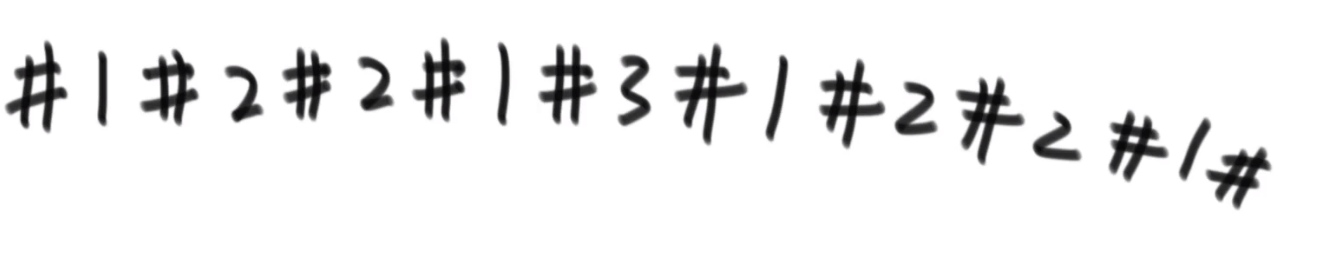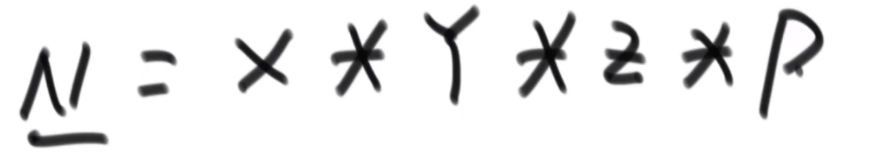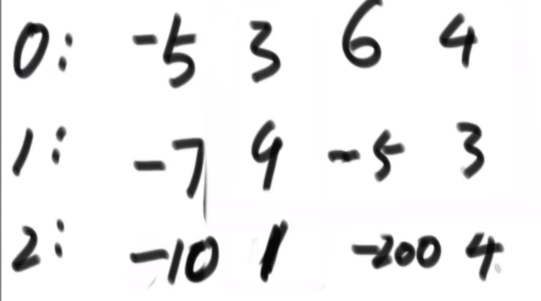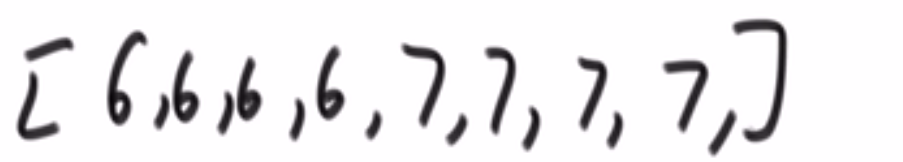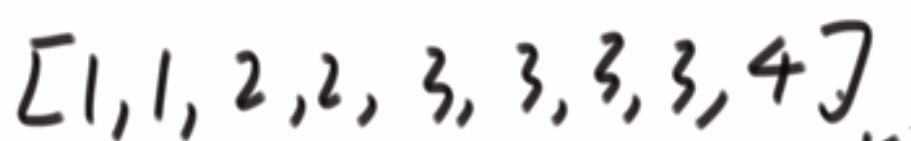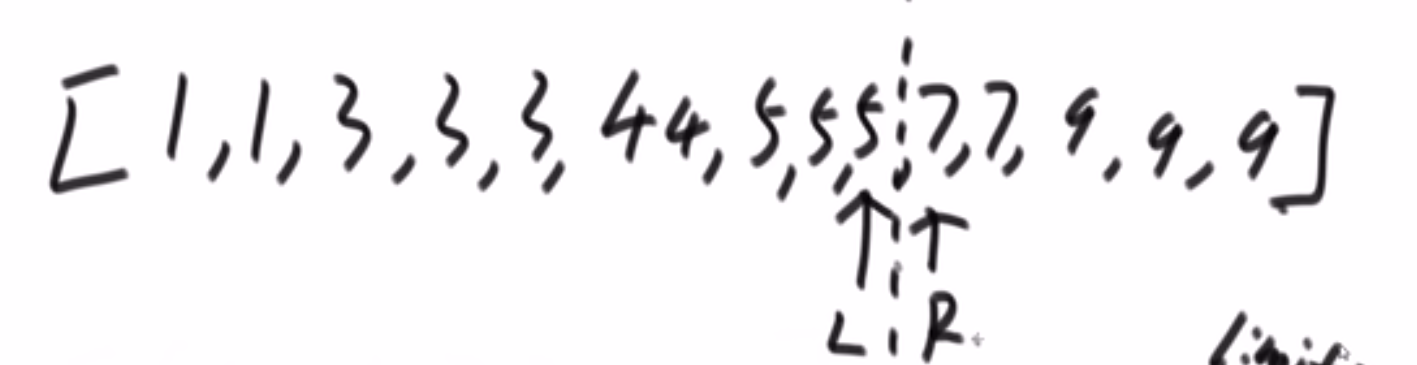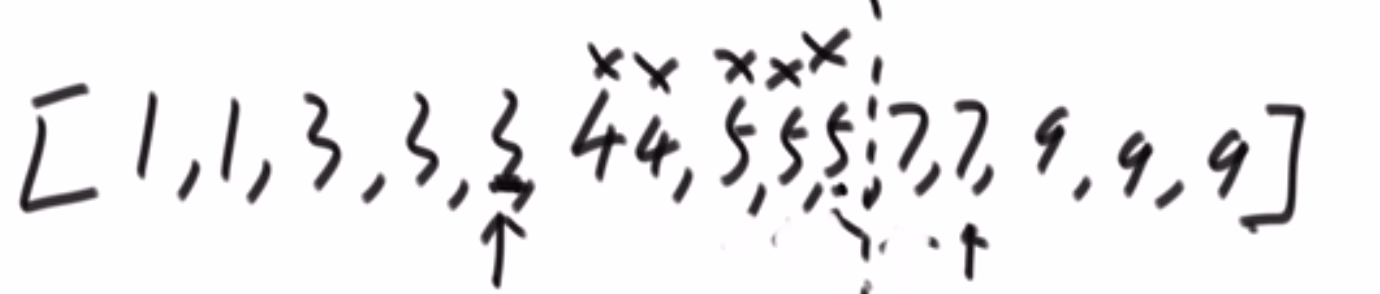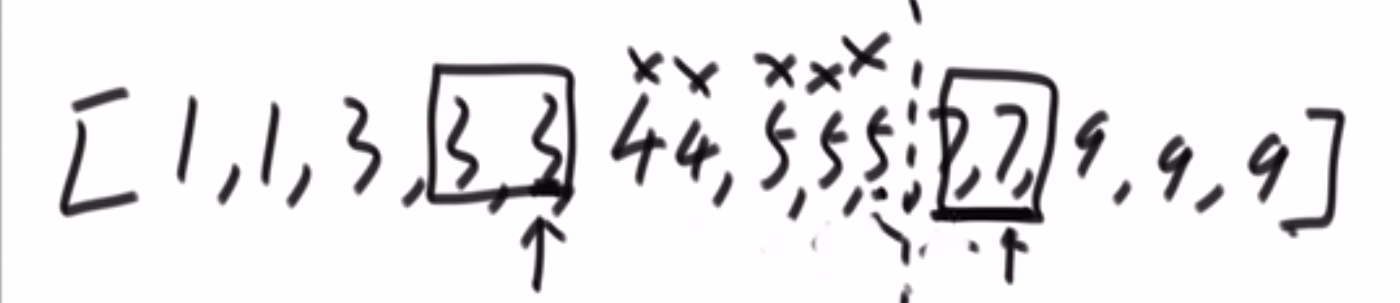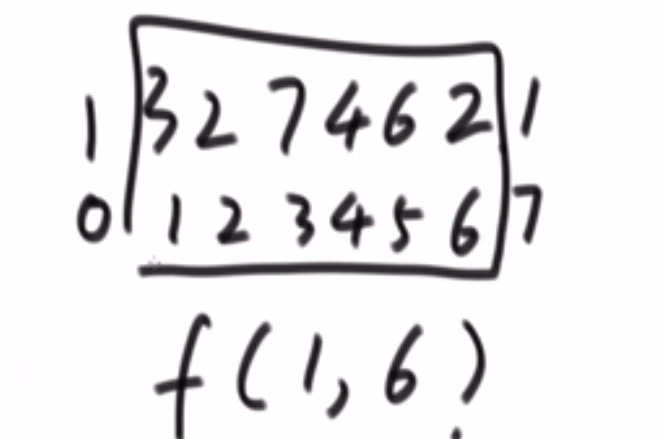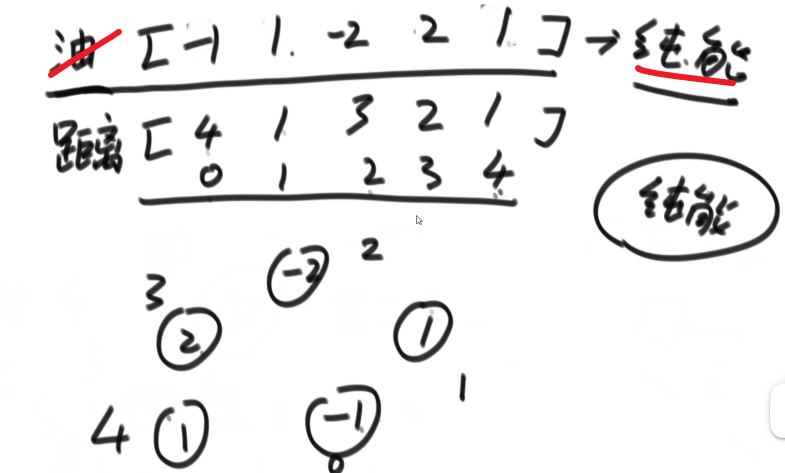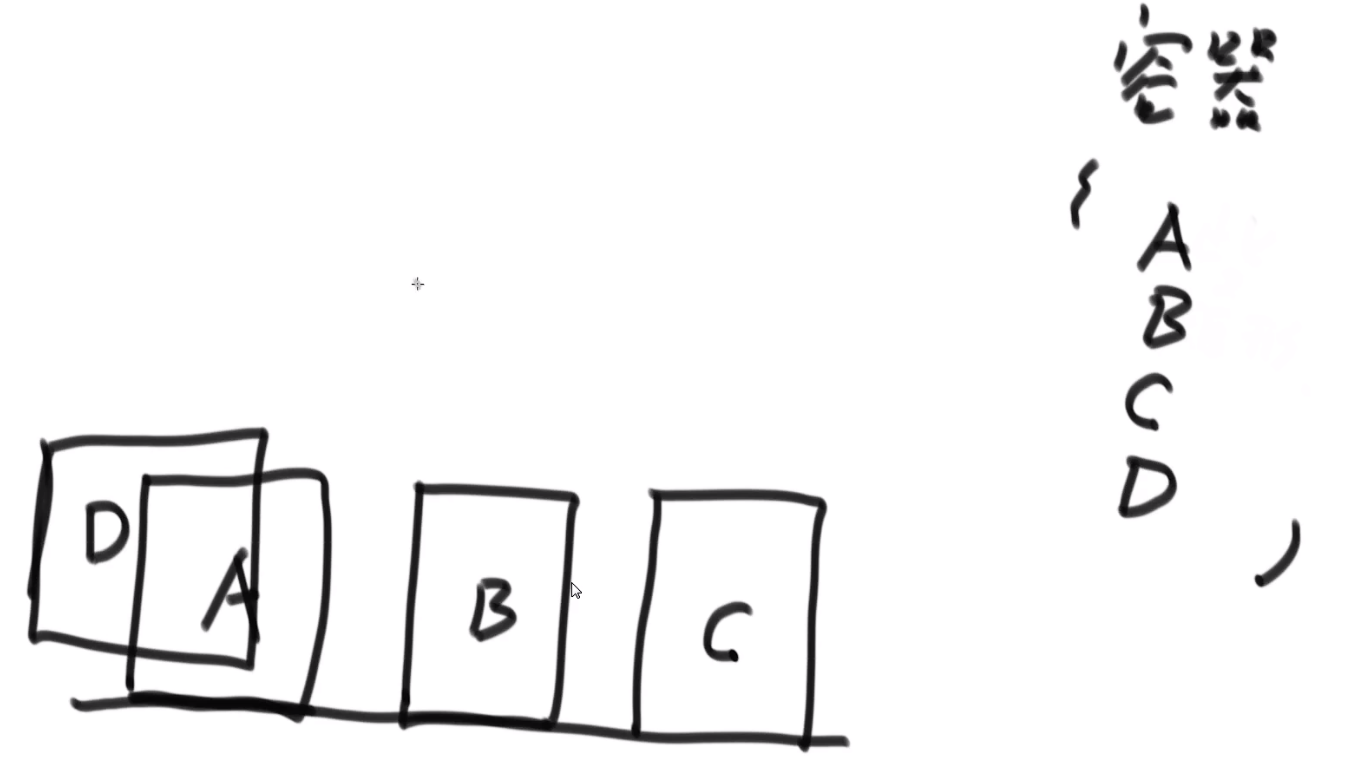My ultimate data structure and algorithm guide
# 前言
此笔记是按照 b 站左程云左神讲的课做的笔记
从初级班班内容到高级班,此笔记应该是对该视频最全的笔记,内涵题目代码讲解以及一些个人思想 (废话)
- 模板部分主要是为了参加比赛的同学方便截取
- 个人看法部分是一些我自己做的题
- 算法课以及刷题以及技巧为视频的初级中级以及高级版的内容 (按照顺序)
之后还会按照代码随想录出一篇个人刷题的记录以及刷题思想,敬请期待!
写笔记不易,求个点赞!
# 模板
# 二叉树
据不完全总结,二叉树的题大致可以分为两种,一种是通过前序、中序、后序、层序遍历来解决问题。
另一种为递归问题,需要从每个节点来获取信息,然后提取出题目中要求的信息
# 遍历模版
# 二叉树非递归遍历
# 中序
- 先找到最左节点,并逐步压栈
- 当最左为空时,弹出栈顶(此时为最左节点),并输出
- 找最左节点有没有右孩子,有则压栈(循环 1,2),没有进行下一步
- 没有右孩子时,当前节点为 null,弹出栈顶(此时栈顶为最左节点的父亲节点)
- 输出 最左节点的父亲节点 的值
- 找 5 中的节点有没有右孩子 重复(1,2)
- 当栈为空 且 当前遍历的节点为 null 时 ,遍历结束
public List<Integer> inorderTraversal(TreeNode root) {
if(root==null){
return new ArrayList<>();
}
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
while(!stack.isEmpty() || root!=null){
if(root!=null){
stack.push(root);
root=root.left;
}else{
root=stack.pop();
list.add(root.val);
root=root.right;
}
}
return list;
}
# 前序
public List<Integer> preorderTraversal(TreeNode root) {
if(root==null){
return new ArrayList<>();
}
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
if(node.right!=null){
stack.push(node.right);
} list.add(node.val);
if(node.left!=null){
stack.push(node.left);
}
}
return list;
}
# 后序
public List<Integer> postorderTraversal(TreeNode root) {
if(root==null){
return new ArrayList<>();
}
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
Stack<Integer> temp =new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
if(node.left!=null){
stack.push(node.left);
}
temp.push(node.val);
if(node.right!=null){
stack.push(node.right);
}
}
while(!temp.isEmpty()){
list.add(temp.pop());
}
return list;
}
# 层次遍历非递归
很多求层相关的问题都可以使用此模版解题
public List<List<Integer>> resList = new ArrayList<List<Integer>>();
public List<List<Integer>> levelOrder(TreeNode root) {
checkFun02(root);
return resList;
}
public void checkFun02(TreeNode node) {
if (node == null) return;
Queue<TreeNode> que = new LinkedList<TreeNode>();
que.offer(node);
while(!que.isEmpty()){
List<Integer> itemList = new ArrayList<Integer>();
int len = que.size();
while (len > 0) {
TreeNode tmpNode = que.poll();
itemList.add(tmpNode.val);
if (tmpNode.left != null) que.offer(tmpNode.left);
if (tmpNode.right != null) que.offer(tmpNode.right);
len--;
}
resList.add(itemList);
}
}
# 注意事项
求二叉树对称的时候就是把两个树的节点同时加入队列进行比较
遇到在二叉搜索树上求什么最值,求差值之类的,都要思考一下二叉搜索树可是有序的,要利用好这一特点
迭代法中,一般一起操作两个树都是使用队列模拟类似层序遍历,同时处理两个树的节点,这种方式最好理解,如果用模拟递归的思路的话,要复杂一些。
大多数二叉搜索树的题目,其实都离不开中序遍历,因为这样就是有序的
# 递归模版
可以解决面试中绝大多数的二叉树问题尤其是树型 dp 问题
本质是利用递归遍历二叉树的便利性
# 递归套路步骤
- 假设以 X 节点为头,假设可以向 X 左树和 X 右树要任何信息
- 在上一步的假设下,讨论以 X 为头节点的树,得到答案的可能性 (最重要)
- 列出所有可能性后,确定到底需要向左树和右树要什么样的信息
- 把左树信息和右树信息求全集,就是任何一 一棵子树都需要返回的信息 S
- 递归函数都返回 S,每一棵子树都这么要求
- 写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息
# 图
# 图:
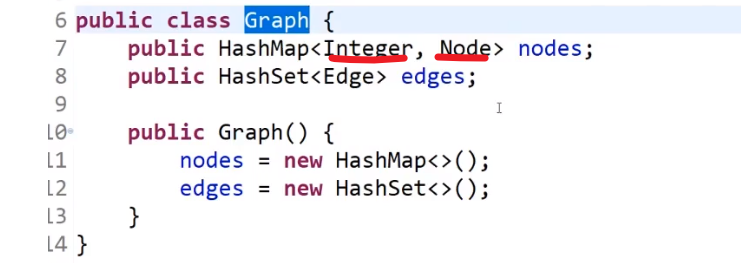
public class Graph {
public HashMap<Integer,Node> nodes;//点的集合
public HashSet<Edge> edges;//边的集合
public Graph() {
nodes = new HashMap<>();
edges = new HashSet<>();
}
}
# 点:
public class Node {
public int value;//节点的数值
public int in;//入度(有多少个节点指向我)
public int out;//出度(我指向多少个节点)
public ArrayList<Node> nexts;//从我出发能到达的下一级节点,邻居节点
public ArrayList<Edge> edges;//从我出发发散出的边的集合
public Node(int value) {
this.value = value;
in = 0;
out = 0;
nexts = new ArrayList<>();
edges = new ArrayList<>();
}
}# 边:
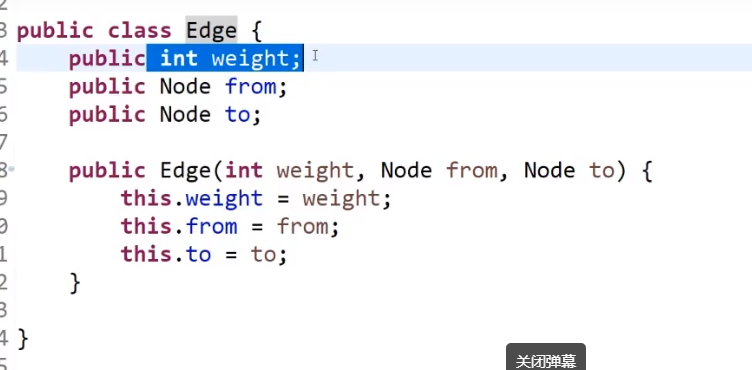
public class Edge {
public int weight;//这个边的权重是多少
public Node from;//这个边从哪里出发
public Node to;//这个边到达哪里的
public Edge(int weight, Node from, Node to) {
this.weight = weight;
this.from = from;
this.to = to;
}
}# 图生成器 (接口,这个要按需求以及输入的来改变):
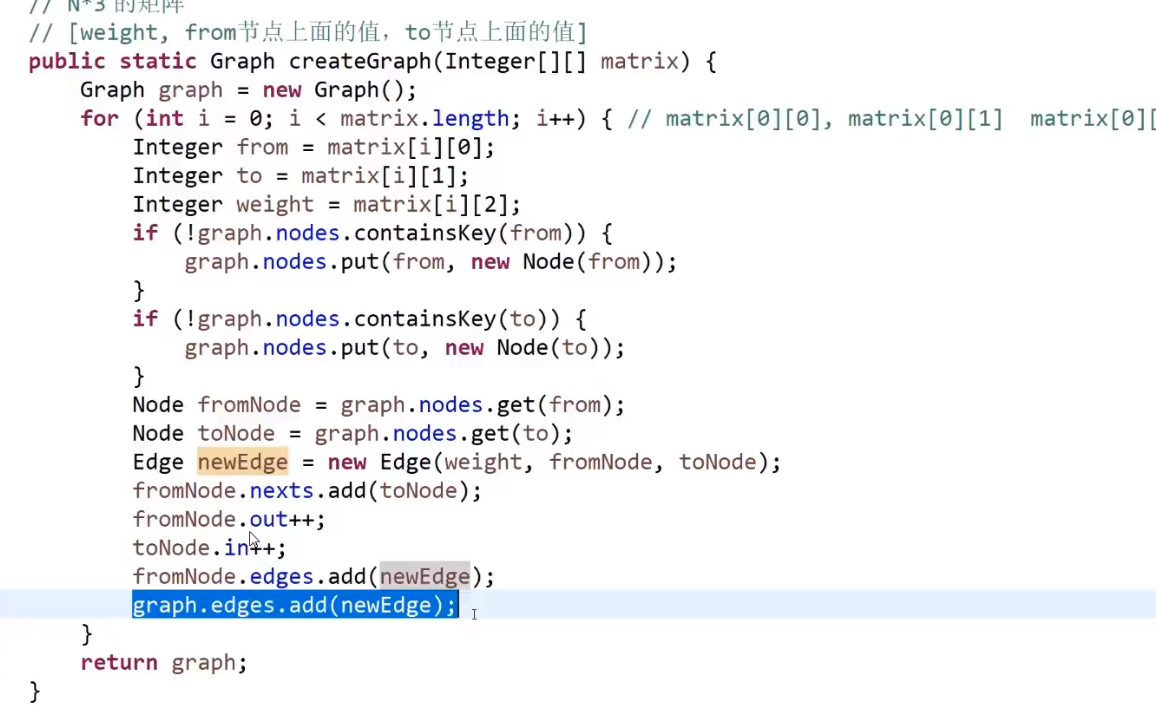
public class GraphGenerator {
public static Graph createGraph(Integer[][] matrix) {//输入一个矩阵
Graph graph = new Graph();//初始化自定义的图
for (int i = 0; i < matrix.length; i++) {
Integer weight = matrix[i][0];//边的权重
Integer from = matrix[i][1];//from节点的序列
Integer to = matrix[i][2];//to节点的序列
if (!graph.nodes.containsKey(from)) {//先检查from节点存在否,不存在就建
graph.nodes.put(from, new Node(from));
}
if (!graph.nodes.containsKey(to)) {//再检查to节点存在否,不存在就建立
graph.nodes.put(to, new Node(to));
}
Node fromNode = graph.nodes.get(from);//拿出from点
Node toNode = graph.nodes.get(to);//拿出to点
Edge newEdge = new Edge(weight, fromNode, toNode);//建立新的边
fromNode.nexts.add(toNode);//from的邻接点增加了一个to节点
fromNode.out++;//from的出度加1
toNode.in++;//to节点的入度加1
fromNode.edges.add(newEdge);//from节点的边集增加
graph.edges.add(newEdge);//加到整个图的边集里
}
return graph;
}
}# 对数器
使用对数器,具体步骤:
1)有一个你想要测的方法 a
2)实现一个绝对正确但是复杂度不好的方法 b
3) 实现一个随机样本产生器
4)实现比对的方法
5)把方法 a 和方法 b 比对很多次来验证方法 a 是否正确。
6)如果有一个样本使得比对出错,打印样本分析是哪个方法出 错
7)当样本数量很多时比对测试依然正确,可以确定方法 a 已经 正确。
好处:
验证方法对不对
可以很快找到错误 case(几千几万 case 中)
判断贪心对不对
具体实现(例如测试冒泡排序方法是否正确):
想要测试冒泡排序方法 a(判断该方法是否正确):
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {//范围每次缩减1,因为每次都排好了一个数
for (int i = 0; i < e; i++) {//从头到e进行两两比较
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);//(前面比后面大就进行交换)
}
}
}
}
public static void swap(int[] arr, int i, int j) {//两两交换
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}# 1)产生一个长度随机的数组(可能为正,也可能为负,0)
随机样本产生器:
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}# 2)绝对正确的方法
调用函数自带的排序方法(实现一个绝对正确但是复杂度不好的方法 b,用于和冒泡排序测试方法比较,判断测试方法是否正确)
public static void comparator(int[] arr) {
Arrays.sort(arr);
}# 3)大样本测试
public static void main(String[] args) {
int testTime = 500000;//测试次数
int maxSize = 100;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);//产生随机数组
int[] arr2 = copyArray(arr1);
bubbleSort(arr1);//测试的方法
comparator(arr2);//绝对正确的方法
if (!isEqual(arr1, arr2)) {
succeed = false;
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
}
public static boolean isEqual(int[] arr1, int[] arr2) {//实现比对的方法 ,比较两个数组的每个数是否相等
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
# 回溯模板
# Subsets
https://leetcode.com/problems/subsets/
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
backtrack(list, new ArrayList<>(), nums, 0);
return list;
}
private void backtrack(List<List<Integer>> list , List<Integer> tempList, int [] nums, int start){
list.add(new ArrayList<>(tempList));
for(int i = start; i < nums.length; i++){
tempList.add(nums[i]);
backtrack(list, tempList, nums, i + 1);
tempList.remove(tempList.size() - 1);
}
}# Subsets II (contains duplicates)
https://leetcode.com/problems/subsets-ii/
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
backtrack(list, new ArrayList<>(), nums, 0);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, int start){
list.add(new ArrayList<>(tempList));
for(int i = start; i < nums.length; i++){
if(i > start && nums[i] == nums[i-1]) continue; // skip duplicates
tempList.add(nums[i]);
backtrack(list, tempList, nums, i + 1);
tempList.remove(tempList.size() - 1);
}
} # Permutations
https://leetcode.com/problems/permutations/
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
// Arrays.sort(nums); // not necessary
backtrack(list, new ArrayList<>(), nums);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums){
if(tempList.size() == nums.length){
list.add(new ArrayList<>(tempList));
} else{
for(int i = 0; i < nums.length; i++){
if(tempList.contains(nums[i])) continue; // element already exists, skip
tempList.add(nums[i]);
backtrack(list, tempList, nums);
tempList.remove(tempList.size() - 1);
}
}
} # Permutations II (contains duplicates)
https://leetcode.com/problems/permutations-ii/
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
backtrack(list, new ArrayList<>(), nums, new boolean[nums.length]);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, boolean [] used){
if(tempList.size() == nums.length){
list.add(new ArrayList<>(tempList));
} else{
for(int i = 0; i < nums.length; i++){
if(used[i] || i > 0 && nums[i] == nums[i-1] && !used[i - 1]) continue;
used[i] = true;
tempList.add(nums[i]);
backtrack(list, tempList, nums, used);
used[i] = false;
tempList.remove(tempList.size() - 1);
}
}
}# Combination Sum
https://leetcode.com/problems/combination-sum/
public List<List<Integer>> combinationSum(int[] nums, int target) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
backtrack(list, new ArrayList<>(), nums, target, 0);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, int remain, int start){
if(remain < 0) return;
else if(remain == 0) list.add(new ArrayList<>(tempList));
else{
for(int i = start; i < nums.length; i++){
tempList.add(nums[i]);
backtrack(list, tempList, nums, remain - nums[i], i); // not i + 1 because we can reuse same elements
tempList.remove(tempList.size() - 1);
}
}
}# Combination Sum II (can’t reuse same element)
https://leetcode.com/problems/combination-sum-ii/
public List<List<Integer>> combinationSum2(int[] nums, int target) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
backtrack(list, new ArrayList<>(), nums, target, 0);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, int remain, int start){
if(remain < 0) return;
else if(remain == 0) list.add(new ArrayList<>(tempList));
else{
for(int i = start; i < nums.length; i++){
if(i > start && nums[i] == nums[i-1]) continue; // skip duplicates
tempList.add(nums[i]);
backtrack(list, tempList, nums, remain - nums[i], i + 1);
tempList.remove(tempList.size() - 1);
}
}
} # Palindrome Partitioning
https://leetcode.com/problems/palindrome-partitioning/
public List<List<String>> partition(String s) {
List<List<String>> list = new ArrayList<>();
backtrack(list, new ArrayList<>(), s, 0);
return list;
}
public void backtrack(List<List<String>> list, List<String> tempList, String s, int start){
if(start == s.length())
list.add(new ArrayList<>(tempList));
else{
for(int i = start; i < s.length(); i++){
if(isPalindrome(s, start, i)){
tempList.add(s.substring(start, i + 1));
backtrack(list, tempList, s, i + 1);
tempList.remove(tempList.size() - 1);
}
}
}
}
public boolean isPalindrome(String s, int low, int high){
while(low < high)
if(s.charAt(low++) != s.charAt(high--)) return false;
return true;
} # 代码随想录
# 二分查找法
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n; // 我们定义target在左闭右开的区间里,[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,因为是左闭右开的区间,nums[middle]一定不是我们的目标值,所以right = middle,在[left, middle)中继续寻找目标值
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在 [middle+1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值的情况,直接返回下标
}
}
return right;
}
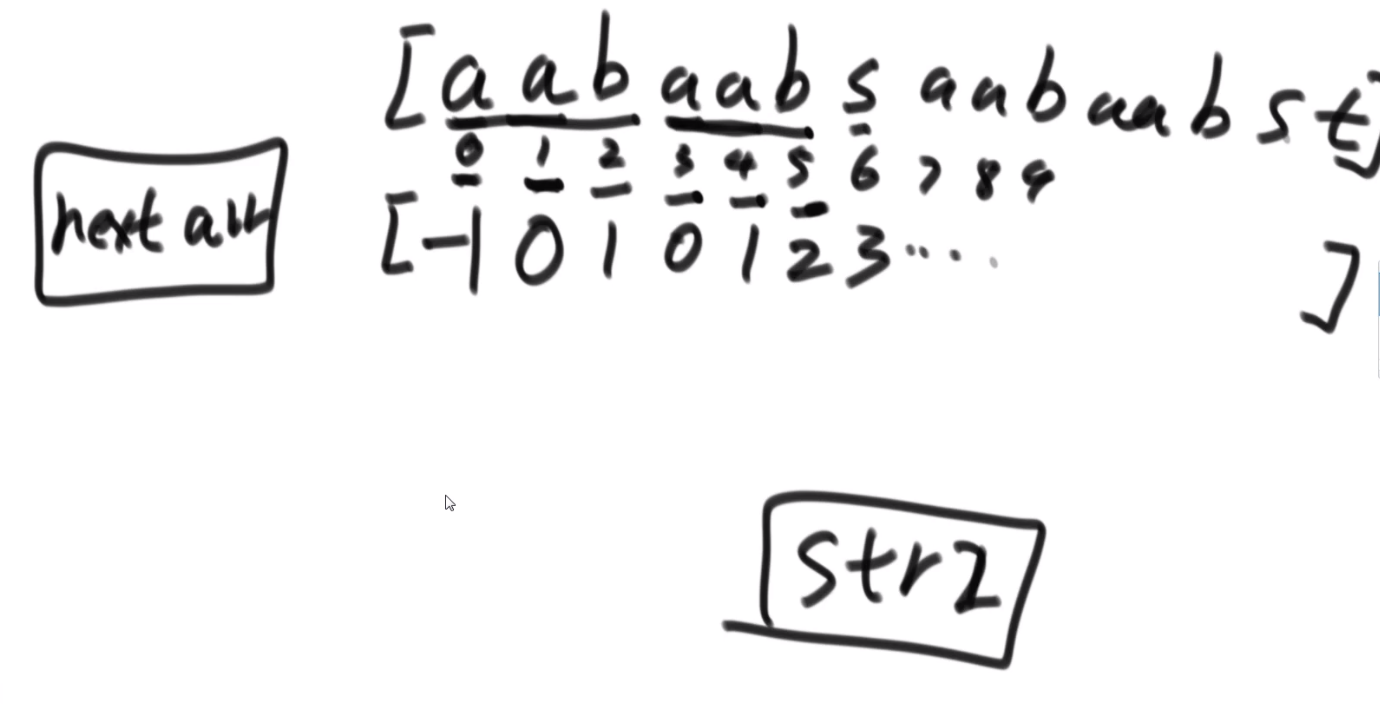
};# #KMP
void kmp(int* next, const string& s){
next[0] = -1;
int j = -1;
for(int i = 1; i < s.size(); i++){
while (j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
if (s[i] == s[j + 1]) {
j++;
}
next[i] = j;
}
}# #二叉树
二叉树的定义:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};# #深度优先遍历(递归)
# 前序遍历(中左右)
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
vec.push_back(cur->val); // 中 ,同时也是处理节点逻辑的地方
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
}# 中序遍历(左中右)
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec); // 左
vec.push_back(cur->val); // 中 ,同时也是处理节点逻辑的地方
traversal(cur->right, vec); // 右
}# 后序遍历(左右中)
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
vec.push_back(cur->val); // 中 ,同时也是处理节点逻辑的地方
}# #深度优先遍历(迭代法)
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
st.push(node); // 中
st.push(NULL);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val); // 节点处理逻辑
}
}
return result;
}# 中序遍历(左中右)
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result; // 存放中序遍历的元素
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // 右
st.push(node); // 中
st.push(NULL);
if (node->left) st.push(node->left); // 左
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val); // 节点处理逻辑
}
}
return result;
}# 后序遍历(左右中)
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val); // 节点处理逻辑
}
}
return result;
}# #广度优先遍历(队列)
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
for (int i = 0; i < size; i++) {// 这里一定要使用固定大小size,不要使用que.size()
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val); // 节点处理的逻辑
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}# #二叉树深度
int getDepth(TreeNode* node) {
if (node == NULL) return 0;
return 1 + max(getDepth(node->left), getDepth(node->right));
}# #二叉树节点数量
int countNodes(TreeNode* root) {
if (root == NULL) return 0;
return 1 + countNodes(root->left) + countNodes(root->right);
}# #回溯算法
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}# #并查集
int n = 1005; // 根据题意而定
int father[1005];
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
// 判断 u 和 v是否找到同一个根
bool same(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}# 个人看法
# 第一题
-
换个角度思考,比如说找两个数字相加会等于一个数字 (target), 也就是说找那个数字 (target) 减去其中一个数字的数字,这个样子我们可以固定一个数字 (比如说一个 for loop 的 i 每次 iteration 都是固定的) 然后去找 target-i.
-
注意数据结构,看要想干什么,是查询还是什么?查询用什么块?(数组遍历 O (N),hash table 约 O (1) 除非 worst case)
-
如果我们要按照一个数字找跟他相关的比如说这个数字在一个 array 里面的下标可以用一个 hash table (HashMap) 来存他们的 key value pair. 这个样子要是搜查 key (数字) 的时候可以通过他的 hash function 更快的查询到那个 key, 找到那个 key 也可以知道那个 key 的 value (下标) 了.
-
如果我们要把数据传到另外一个数据结构比如说 array to HashMap (hash table) 一般会用到一个 loop 然后挨个传进来,然后再进行操作,想想能不能在传的时候,在那个 loop 里面,直接在传每一个数据之前或者之后进行操作?
- 比如说我们要找像上面的说的 target-i, 必须要有一个数字是固定的 (就让我们这个 loop 本身的数字每个 iteration 的数字固定住), 然后还需要找 target-i. 我们可以直接看这个数字在不在这个新的数据结构里面 (这样就是查询可以像上面的说的用 hash table 更快), 如果已经有了就直接 return, 如果不在 再 把当前这个固定的数字给传进新的数据结构。接下来下一个 iteration 下一个数字固定住,找相对应的 target-i. 这么做是对的因为我们还是会把数据一个一个传进去,所以如果有复合需求的那两个数字在的话,在第一个数字当固定,另外一个数字因为还没放进去所以没有,但是当第二数字当固定,这前面的数字已经放进去了,那就会查到。如果没有复合条件的,那就不会有结果.
# 第二题
- 如果需要的是一个 linkedlist 的第一个 node (他的 next 会指向下一个然后 next 的 next 指向…so on), 不一定需要我们第一个就是那个第一个 node, 我们可以先暂时用一个不是第一个的 node (value 不一样) 来指向第一个 node, 然后返回的时候再
return node.next;就可以得到第一个 node - 如果 linkedlist 已经指向了结尾 (到了 null), 是不是可以认为 value 为 0 然后再继续.
- sum = number1 + number2 + carry(from previous number)
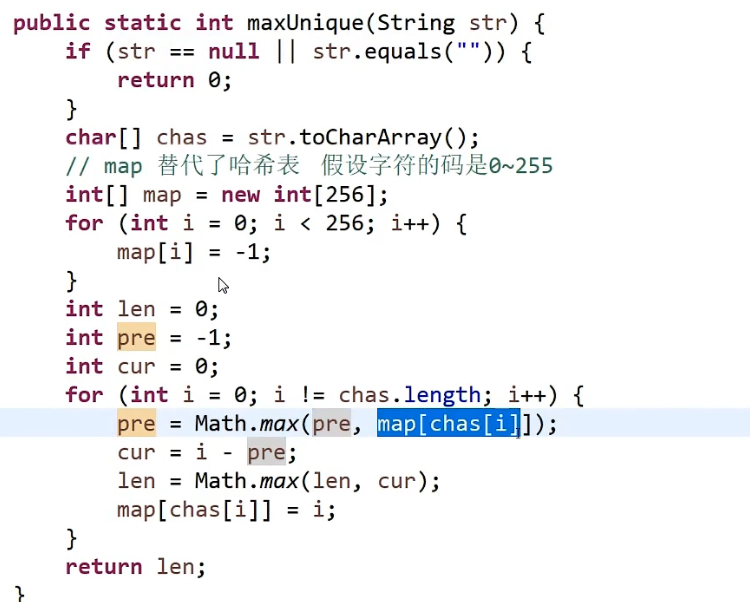
# 第 387. First Unique Character in a String
- 用一个数组,长度 26, 每一个都是存字符串里面出现哪个字符出现几次。比如说下标为 1 的就是‘b’-‘a’, 然后记录着‘b’这个字符出现了几次
- 之后返回哪个存的是 1 的下标对应的字符就行了
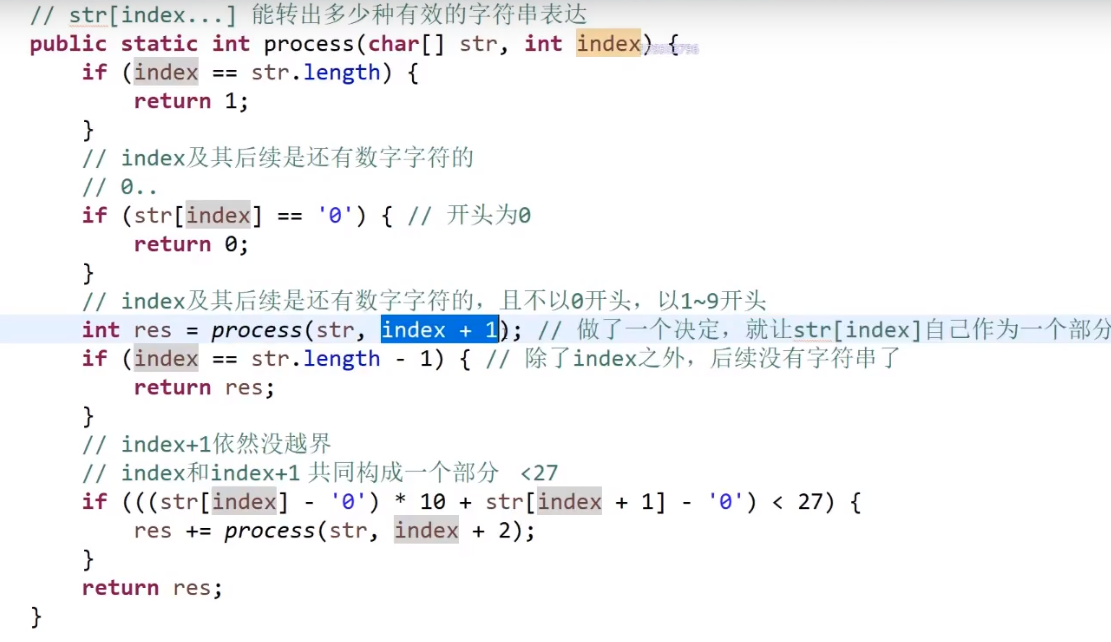
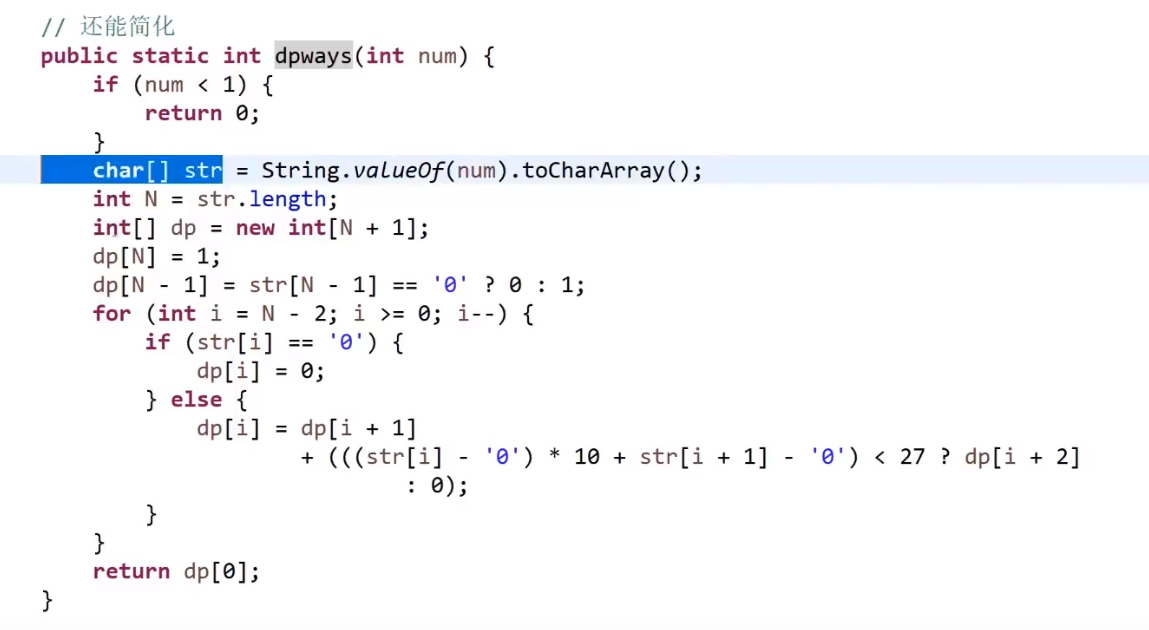
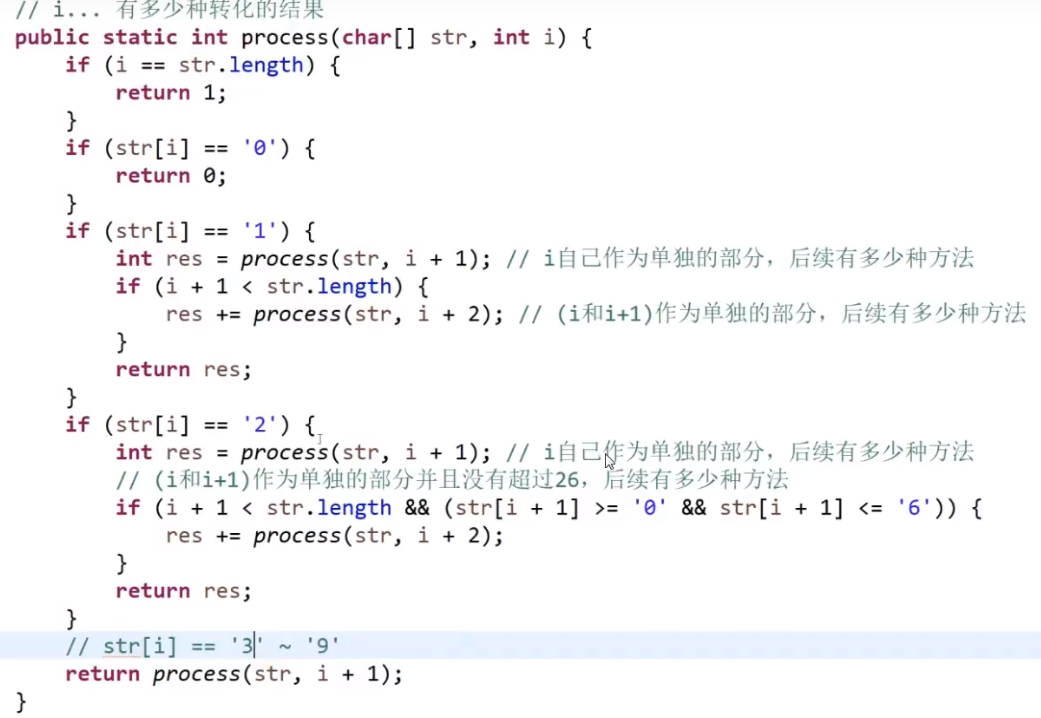
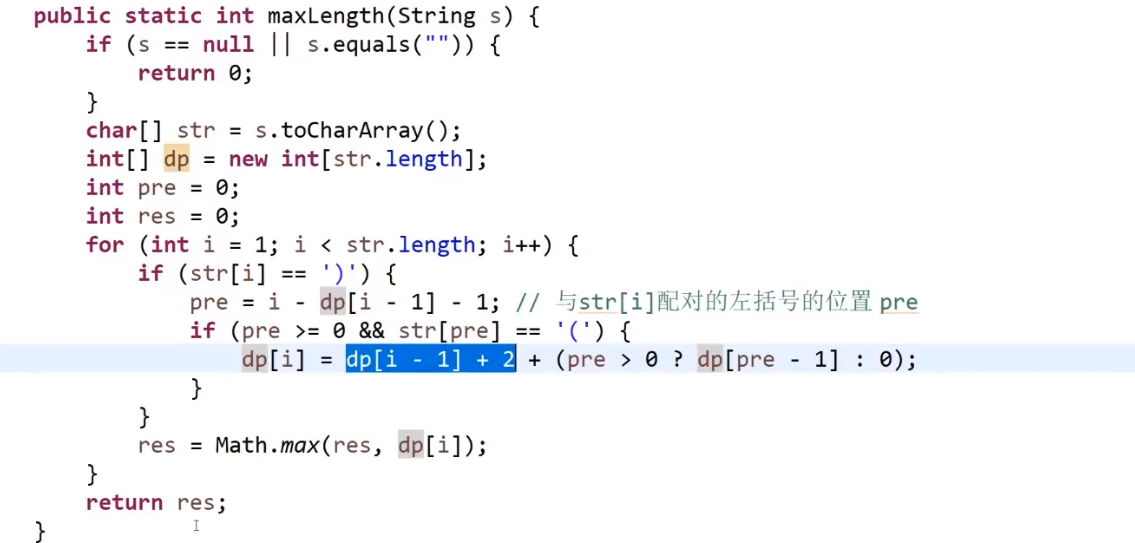
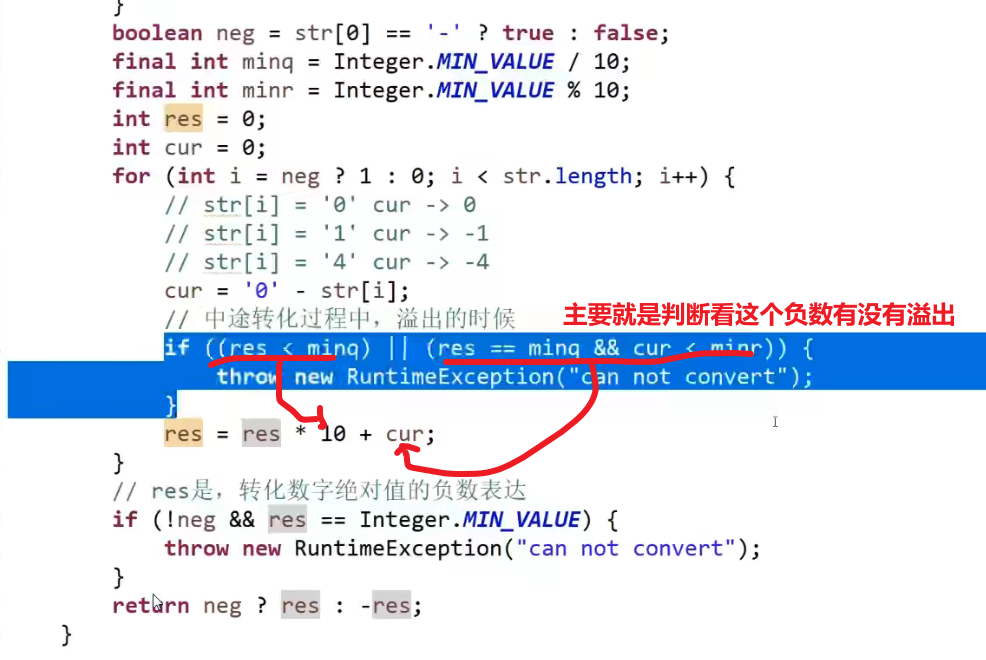
# 第 91. Decode Ways
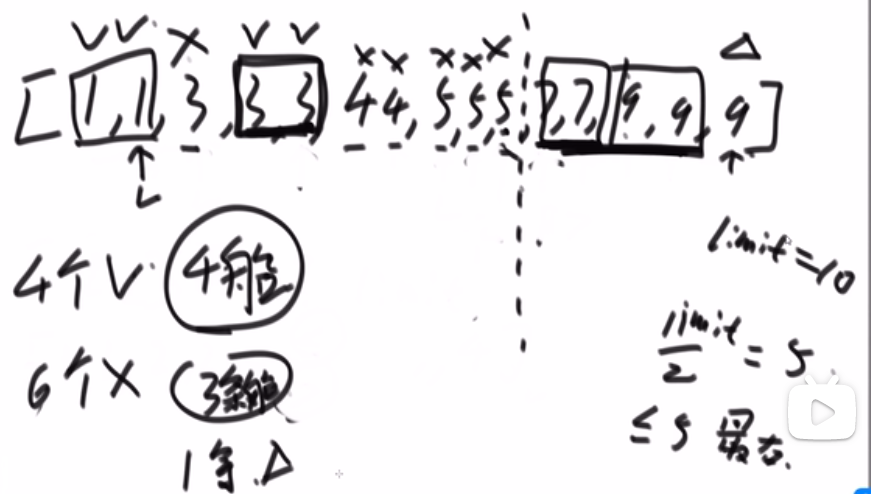
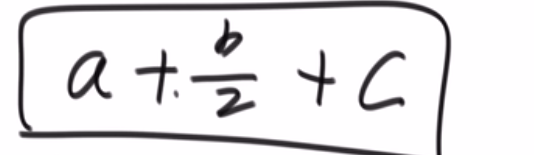
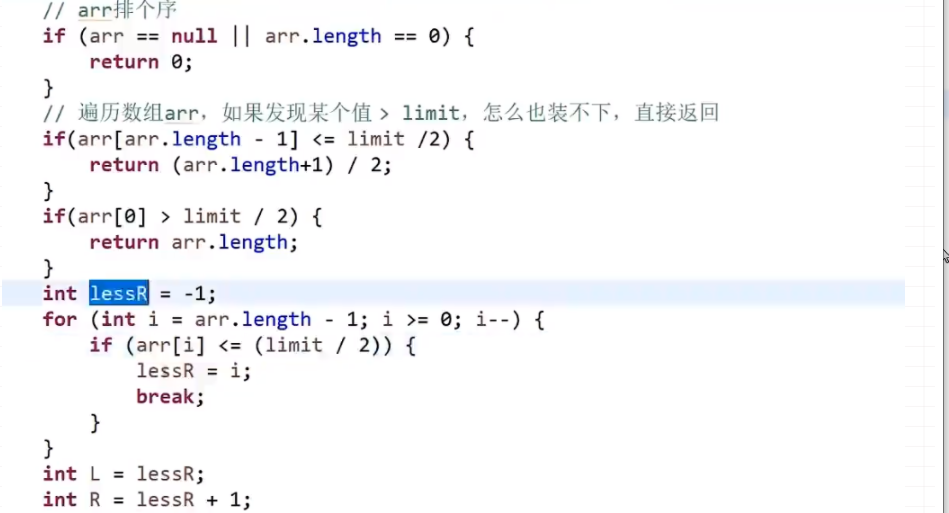
# 第 881. Boats to Save People
- 直接排序然后双指针 O (nlogn)
- 因为说了每条船两个人最多,所以双指针很合适
- 注意我这里用的 res++ 到处都是,其实可以改进,只需要记录双指针,只要 left<=right 就执行,之后其实我们靠 right 指针获取需要多少串,或许用个变量去 track
# 第 300. Longest Increasing Subsequence
序列问题
-
brute force 的话会是所有 subsequence, 这个复杂度为 2n-1 (跟求一个字符串的所有 subset 差不多一样)
-
dp 方法,就是创建一个数组,数组每一个元素代表原数组中当前元素为结尾的最长合法的数组序列长度,最后答案就是 dp 里面最大值,是 O (n2) 因为需要 dp 里面每一个元素都需要往之前的元素找最大的值,才可以知道自己的最大值可以是多少
做法就是两个 for loop, 每一个元素,我们一开始把 dp 对应位置设置为 1, 然后接着 for loop 看 dp 数组里面这个位置之前有多少个比这个小的,每一次遇到就让当前他的值跟那个值 + 1 (代表他自己) 比较,之后要是又遇到了个小的,会接着比,这是因为这个数字存的当前数字作为结尾的数字序列最长长度不一样比后面的数字存的当前数字作为结尾的数字序列最长长度小,因为那个后面的数可能比自己这个数还要小 (但确实是符合那个比我们当前到了的 i 位置的数字要小)
期间我们没处理完一次 dp [i] 我们就查看一下,反正就是保存最大的 dp [i] 值就是答案
注意这个 dp 数组的作用,是记录每一个数作为数字序列结尾的最长长度是多少
-
dp 加 binary search
在这里,dp [i] 存的值代表 i+1 长度的序列中,结尾最小的元素是什么
- 如果当前数是大于我们 dp 数组此时存的最后一个数 (比如说 x 位置), 那直接把当前数加到 dp 数组 (x+1 位置), 说明我们现在 so far 处理的合法的最长数组序列长度增加了一个,然后这个长度最小的元素也就是我们这个新加的
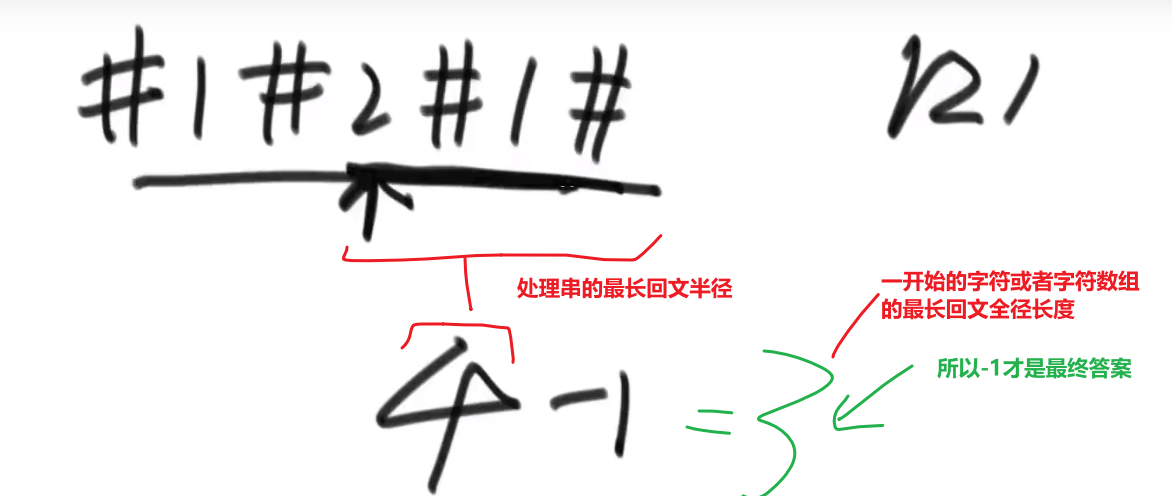
- 如果当前素是小于或者等于我们 dp 数组此时存的最后一个数 (比如说 x 位置), 说明我们之前处理的那些位置有一个位置,有可能被换成当前这个数 (只有这个数比那个数也小的话), 代表当前数才是作为那个长度合法的最长数组序列的最后一个元素是最小的,他能换哪个?他能换当前 dp 数组第一个比他小的 / 或者是跟他数一样的 (dp 数组很明显是升序排序的), 我们可以用 Array.binarySearch 找到那个数 (这个系统函数如果找不到你要找的数,就会返回一个负数,然后你把返回的负数 - 1 然后再 - 1 就是那个第一个比我们找的数要大的数的下标! 新东西!学到了!!!*), 然后把当前数替代那个数
- 之后处理完所有数,答案就是我们的 dp 数组的长度 (如果用的是 arraylist, 如果是数组的话用变量记录什么的就行了)
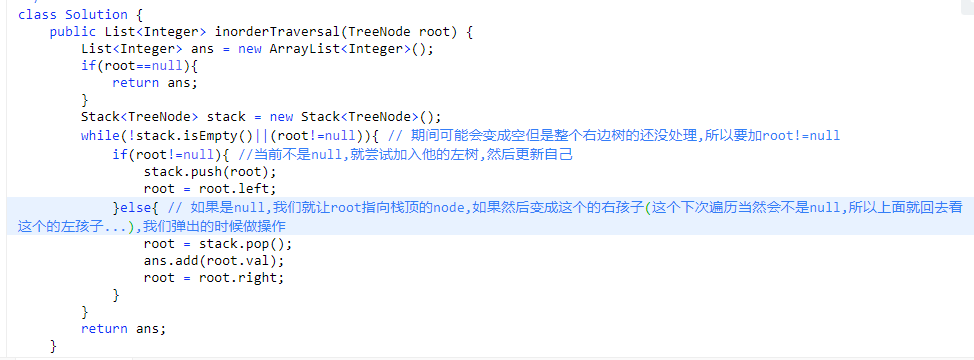
# 第 94. Binary Tree Inorder Traversal
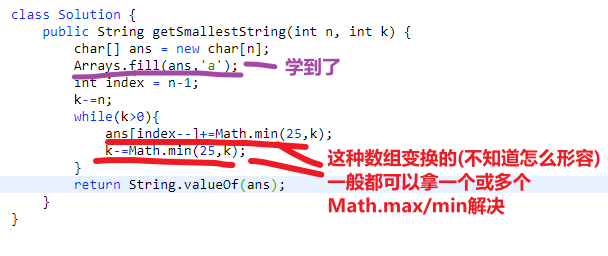
# 第 1663. Smallest String With A Given Numeric Value
- 用一个字符数组,n 的大小,一开始直接设置为全是 a, 然后让 k 值 - n*1
- 之后只要 k 还要比 0 大,就需要把字符数组 (从最后一个开始往前) 变成 z 或者变成 k 值哪个更小边哪个 (可以用 char 直接加 Math.min (25,k))
- 然后当然把 k 更新,就是减去 Math.min (25,k)
- 之后就是 while 循环检查 k 是不是还是大于 0 等等
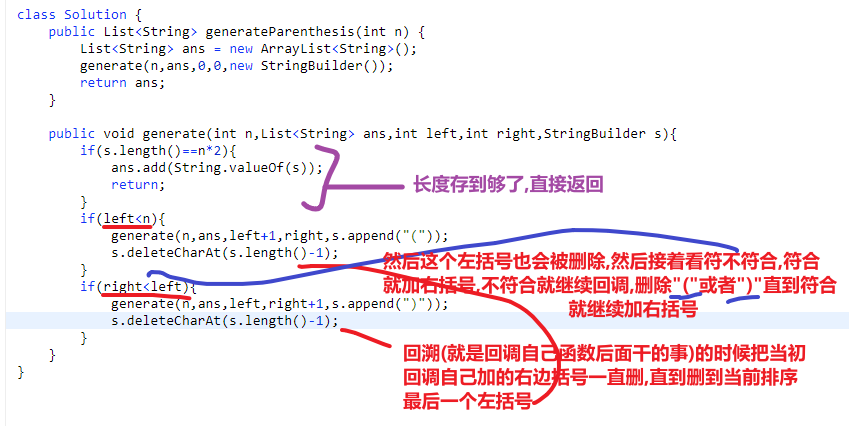
# 第 22. Generate Parentheses
- 回溯方法就是传一个 list 用来存每一个答案,然后每个答案就用 stringbuilder
- 回溯函数还有 max,open 代表当前层穿件来的 sb 有多少左括号,close 代表当前层穿件来的 sb 有多少右括号
- 我们当前 sb 等于 max*2 的话代表找到一个直接加入到 list 里面去
- 否则如果我们左括号加的数量没超过 max 数量我们就一直加,加完回调自己
- 我们右括号在下面,只有右括号没有超过左括号数量时,我们才让右括号增加,然后回调自己
- 每次右括号加完回调完自己都会先经过左括号的判断看看当前层符不符合那个小于 max 的情况
- 注意!!!
- 我们左边在最后是需要清除掉最后一个加的!!!这么做了才能创造其他的可能性
- 我们右边在最后是需要清除掉最后一个加的!!!这么做了才能创造其他的可能性
相当于我们对于当前刚加完的左括号数做完回调之后我们我们把改层加的这个左括号从 sb 去掉,然后再试试加右边括号等等等
同理,我们右边的刚加的可能也需要去掉,这样才有其他的可能性
可以这么想:
- 每一次的排序都是靠着你 ** 所有左边括号 (中间还有可能夹着几个右括号)** 怎么放的,然后对于每种包括着所有左括号之间的排序,我们可以对剩下的 (没被包括住的右括号), 进行增加,一直增加到合适长度就把结果放入 list 里面去
- 因为当前的结果已经放回到 list, 然后就会 return, 一层一层往回走,因为我们之后放的右边括号 (这个判断在下面), 我们在返回的时候就把我们当初一个一个加的右括号从 sb 里面删除
- 直到回溯到我们那个保存的排序的最后一个左括号也被删除了,就会接着往下看此时的 sb 符不符合那个下面加右括号的 if, 如果符合就会添加,此时这个左括号相当于是被之后再加了,等等
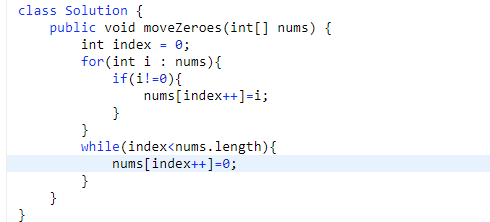
# 第 283. Move Zeroes
- 第一次遍历,保持自己的一个 index, 然后只有当前数组数不是 0 就把放到自己维持的 index 上
- 之后从自己的 index 数到数组长度位置都是 0
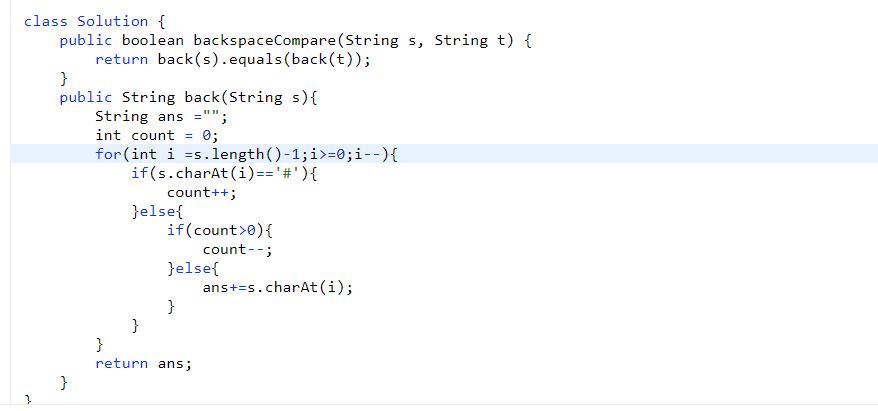
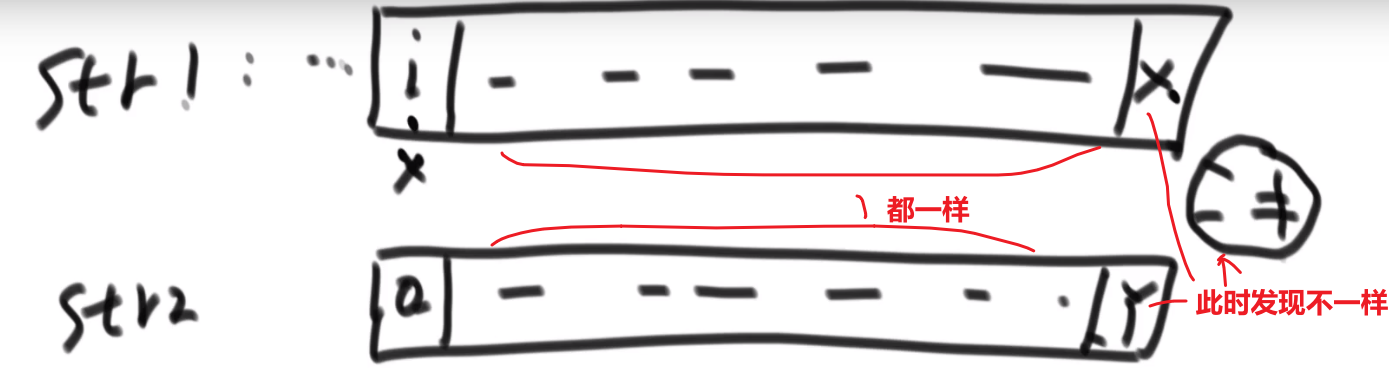
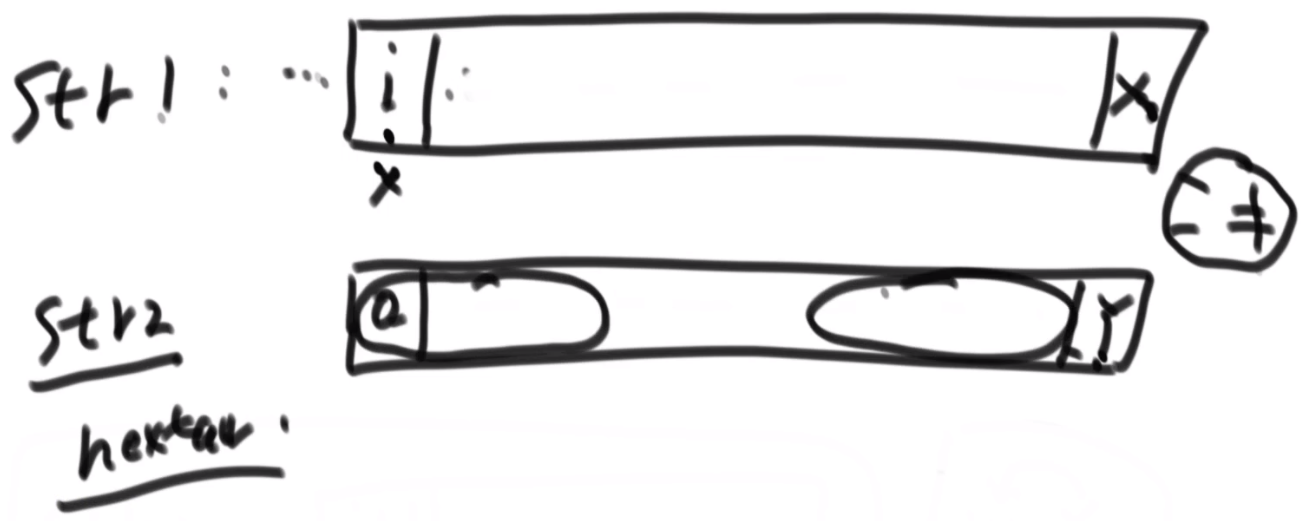
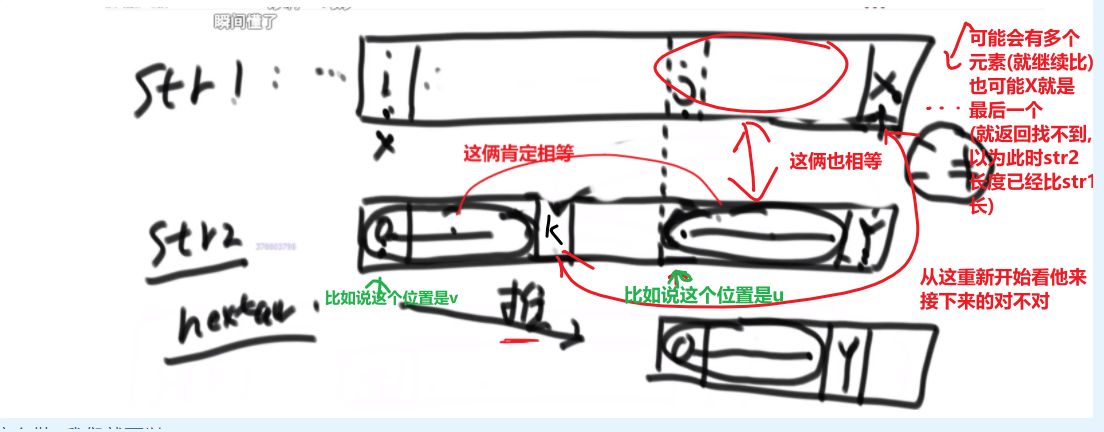
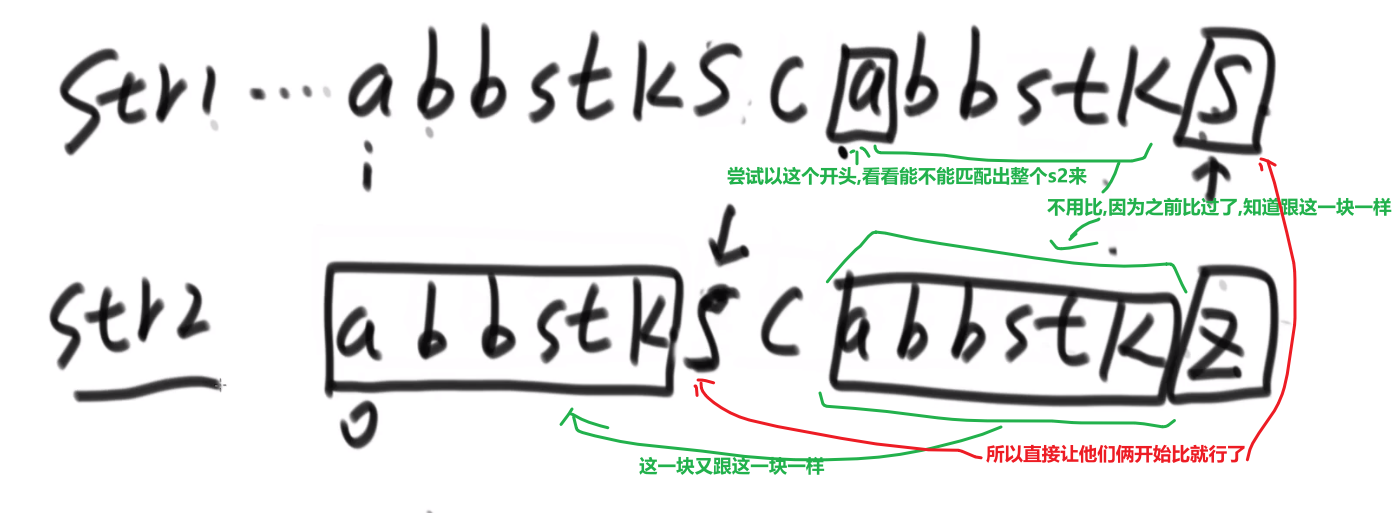
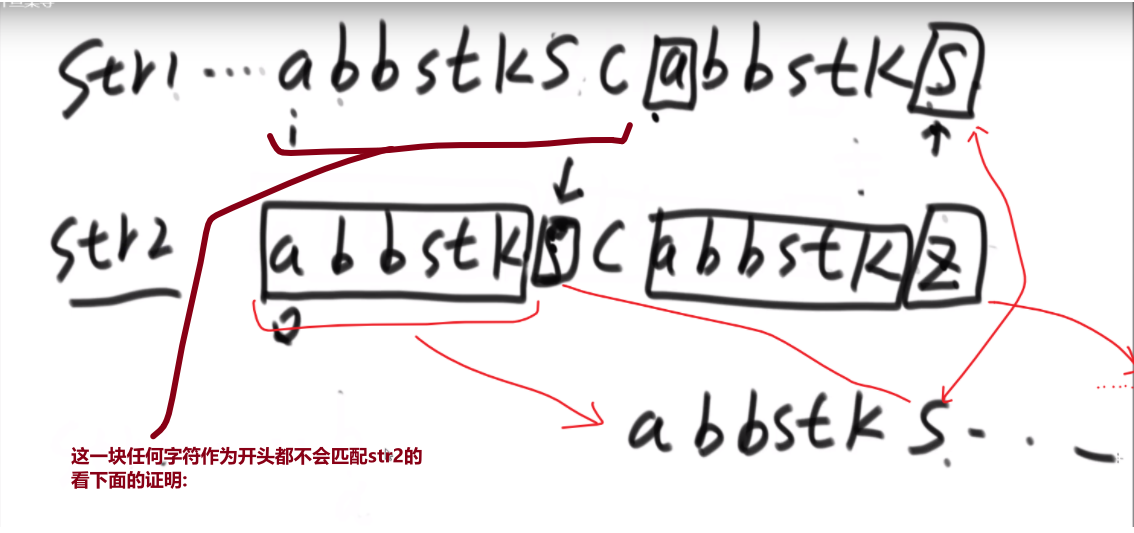
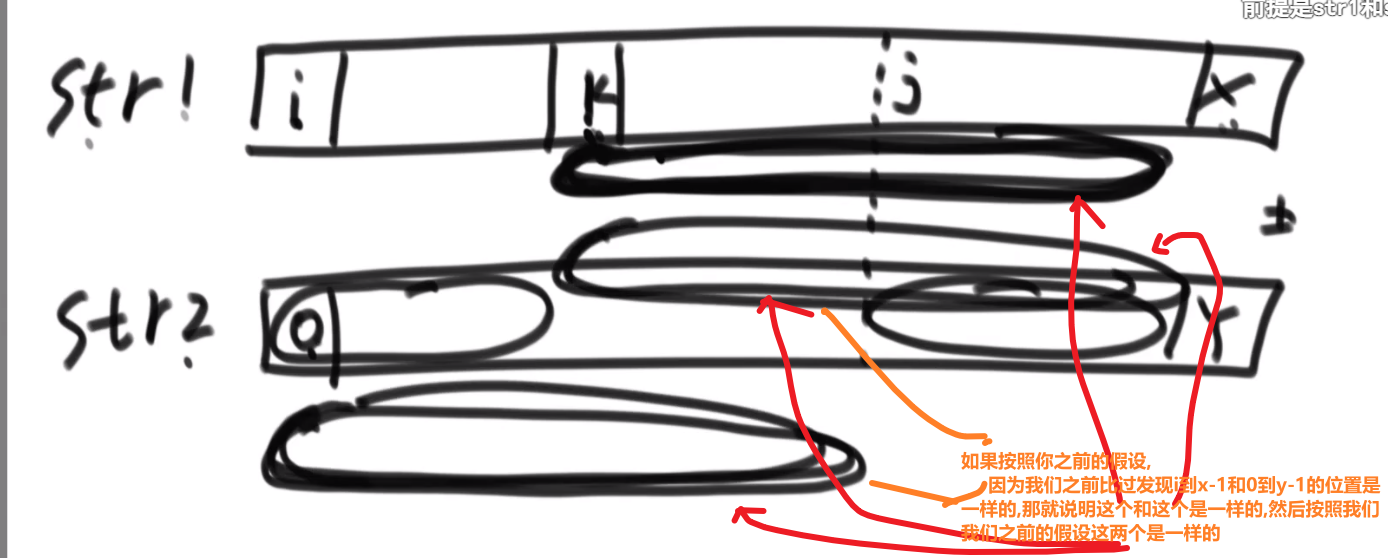
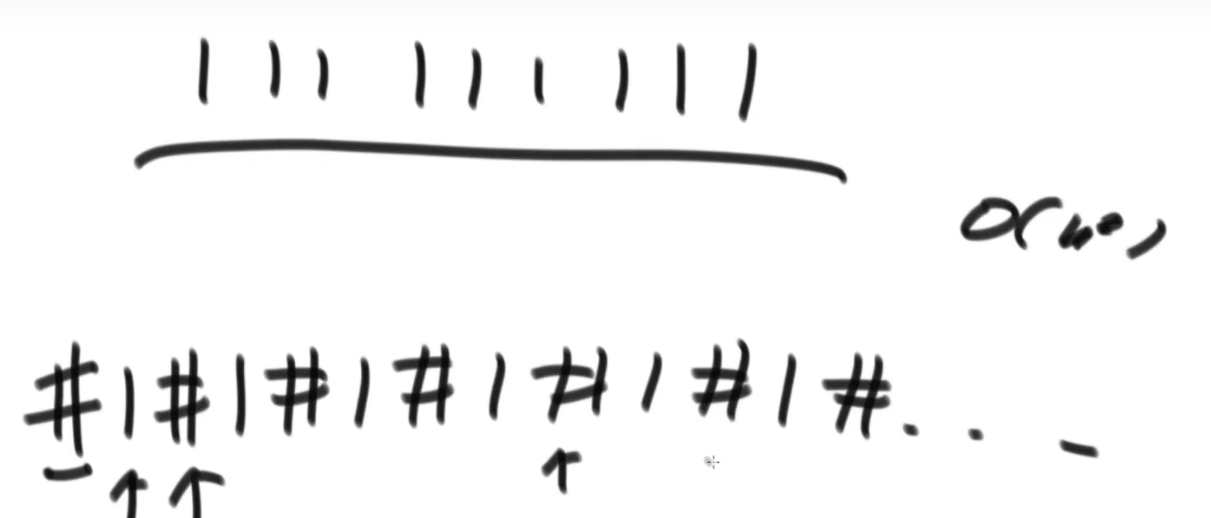
# 第 844. Backspace String Compare
- 从每一个字符串后面开始生成字符串,如果是 #就增加 count
- 要不是 #的话那么只有在 count 为 0 的时候才可以加到字符串
- 为 s 生成字符串,为 t 生成字符串,之后比较他们相不相等就行了
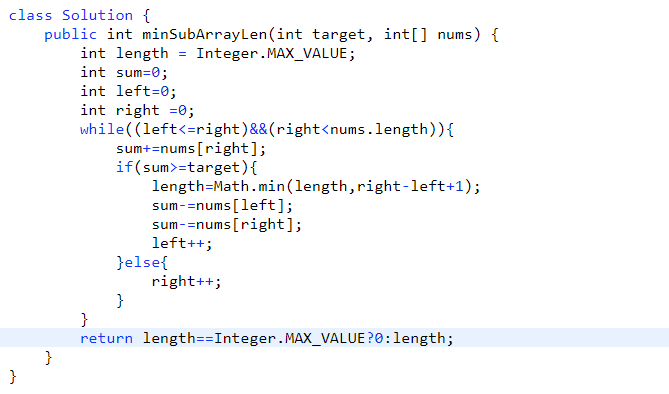
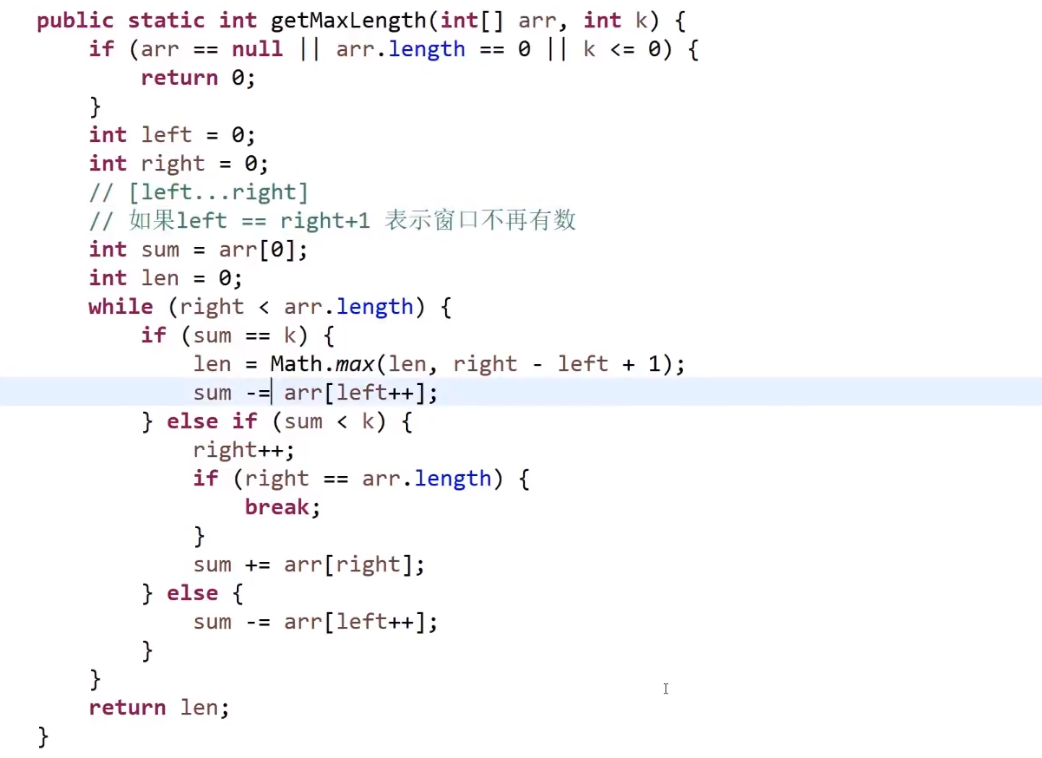
# 第 209. Minimum Size Subarray Sum
- 滑动窗口,规矩定好 (loop 然后里面 if 的更改情况)
# 第 904. Fruit Into Baskets
- 滑动窗口
- 让左指针直接跳到一个位置
- right-left+1 代表目前窗口长度
- right 不一定要停啊等等等
# 算法课
# 异或
# 异或换值
给两个变量的值换过来:
a = a^b
b = a^b
a = a^b注意 a 和 b 可以是一样的数字等等等,但是不可以是同一个,比如说数组里面 a 和 b 不能代表同一个元素
# 异或算一个不一样的
数组有一个数字出现了奇数次,其他的数都是偶数:
int xor = 0;
for (int i =0; i<nums.length; i++){
xor^=nums[i]
}最后 xor 会等于那个出现奇数次的,出现偶数次的数都被自己消除掉了
- 0^N=N
- N^N=0
- a^b=b^a
- a^b^c=a^(b^c)
# 异或算两个不一样的
数组有两个数字出现了奇数次,其他的数都是偶数:
- 我们还是一个奇数次的做法先得到 xor, 那两个出现奇数次的数字 (比如说 a 和 b) 最后 xor 会等于 a^b
- 因为这两个数不一样,所以把他们转换成二进制他们肯定会在某一位上有一个是 0 有一个个是 1
- 0^1=1, 所以 xor (=a^b) 在那个位上也会是 1, 所以我们可以把 xor 的二进制最右边的数字部分获取出来
我们可以使用
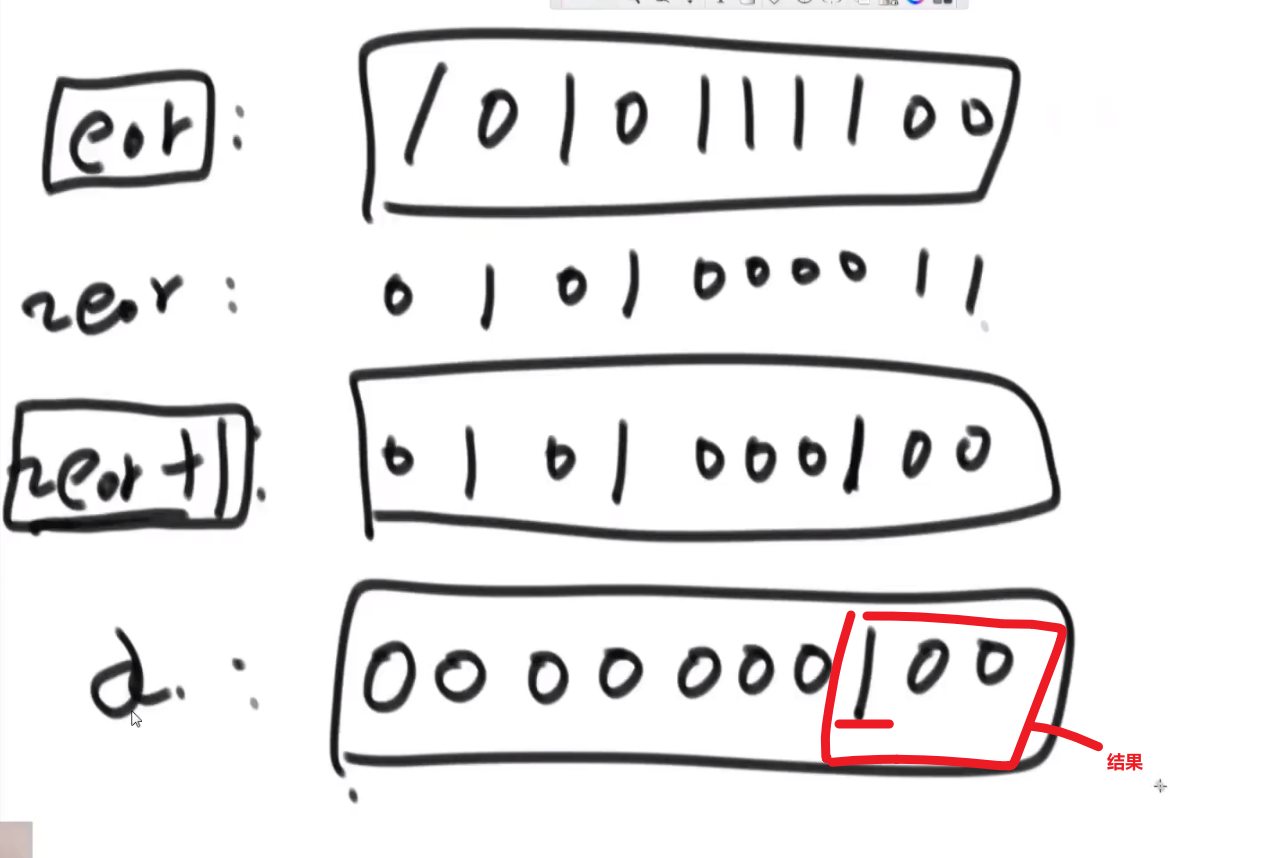
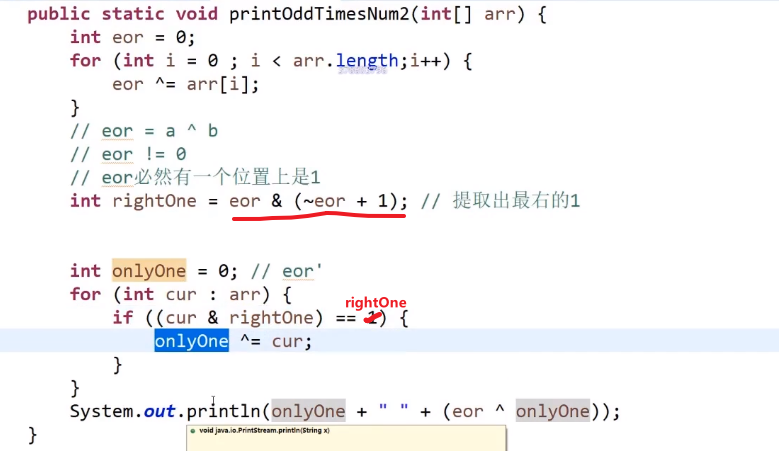
eor & (~eor + 1)这个能提取出这个数 (eor) 的二进制最右边的 1 的数字以及后面转换成十进制的数字
- 我们有了这个数后我们就可以声明一个新变量 xor2 再次遍历数组,然后只有那个元素的结尾那几个我们上面取出来的几位二进制一样才可以让 xor2^= 那个元素 (使用
&判断就行,这个是 bit by bit, 这个细节比较多 (自己去查), 注意只是一个&!!!) - 就算我们这个判断可能会让别的数也判断对,但那也是对于出现偶数次的数,我们知道另外一个出现奇数次的数字不可能在这个对应二进制位置上是一样的 (我们当前这个数的最右边的二进制为 1 的位置在另外一个出现奇数次的数字在那个位置肯定会是 1, 所以我们 xor 的结果在那个二进制位置也才可以是 1)
- 这样我们相当于是给那两个出现奇数次的元素给分成两个组了,然后出现偶数次的不同数字随便分,反正他们会自己消灭自己的 (异或就是这样的)
最后 xor2 得出的就是要么是 a 要么是 b, 我们再 xor^xor2 就可以获得另外一个数字了
# 排序
# 冒泡排序
- 遍历数组
- 每次遍历让所有的元素 (除了最后) 跟下一个元素比,如果出现 inversion 就换过来
- 每次 outerloop 遍历就会让当前没有 sorted 部分找出一个最大元素放到正确的位置上 (被换到那)
不管什么输入都是固定操作,除了最好 case 不需要换的操作
# 选择排序
- 遍历数组
- 每次遍历都要遍历数组没有 sorted 部分找到当前最大 / 最小元素放到正确的位置上
不管什么输入都是固定操作
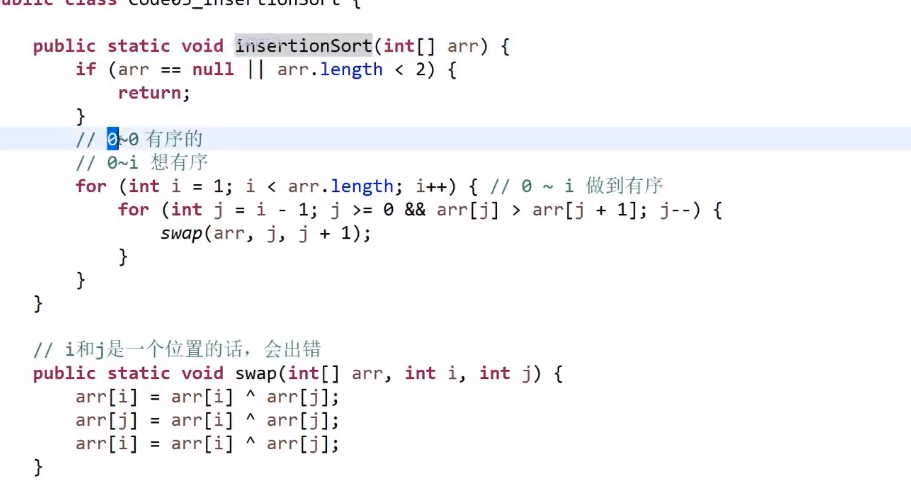
# 插入排序
- 遍历数组
- 首先做到 0-0 有序,这个很明显本身就做到了
- 接着我们要做到 0-1 有序,所以先看在 1 号元素
- 如果比前一个小就交换,交换完了再看前面有没有要交换的了,(前面没数了,也挺了), 我们此时做到了 0-1 有序
- 如果比前一个大,不需要交换
- 接着我们要做到 0-2 有序,所以先看在 2 号元素
- 如果比前一个小就交换,交换完了再看前面有没有要交换的了,一直换到对的地方
- 如果比前一个大,不需要交换
- 接着我们要做到 0-3 有序,所以先看在 3 号元素
- 如果比前一个小就交换,交换完了再看前面有没有要交换的了,一直换到对的地方
- 如果比前一个大,不需要交换
… 最终我们做到了 0-nums.length-1 有序了
这个不像冒泡排序和选择排序是固定操作,如果给的就是有序的,那就比一比就完成了所以会是 O (N), 但我们说时间复杂度都是 worst case 所以还是 O (N^2)
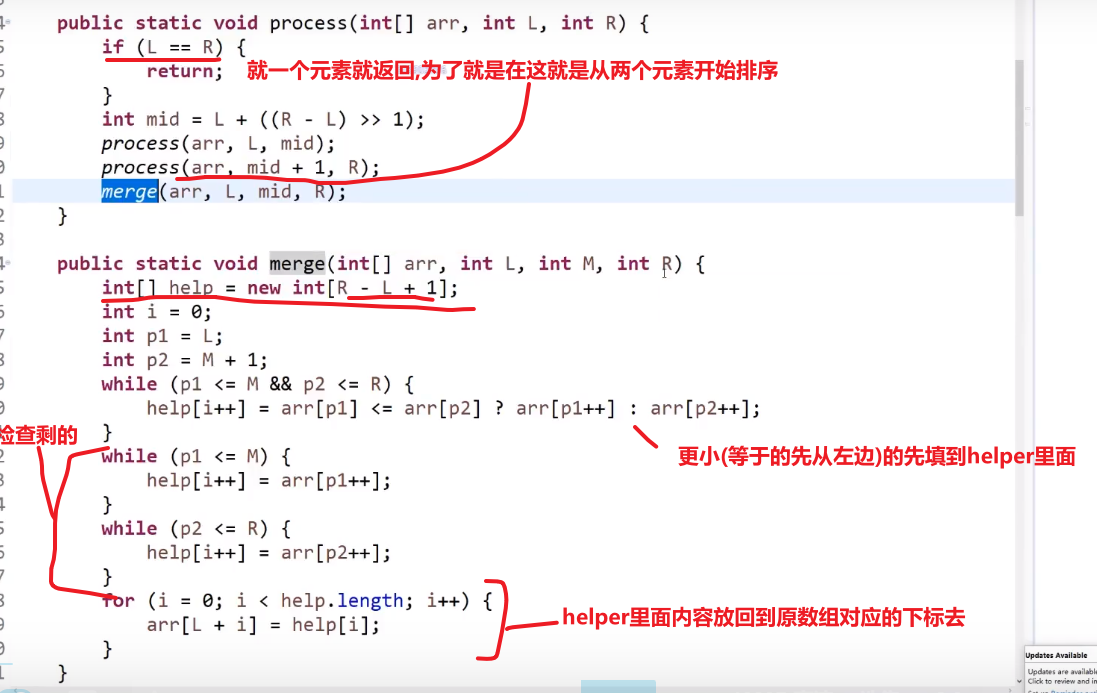
# 归并排序
- 找到当前中心点 mid
- 调用自己排序 left 到 mid
- 调用自己排序 mid+1 到 right
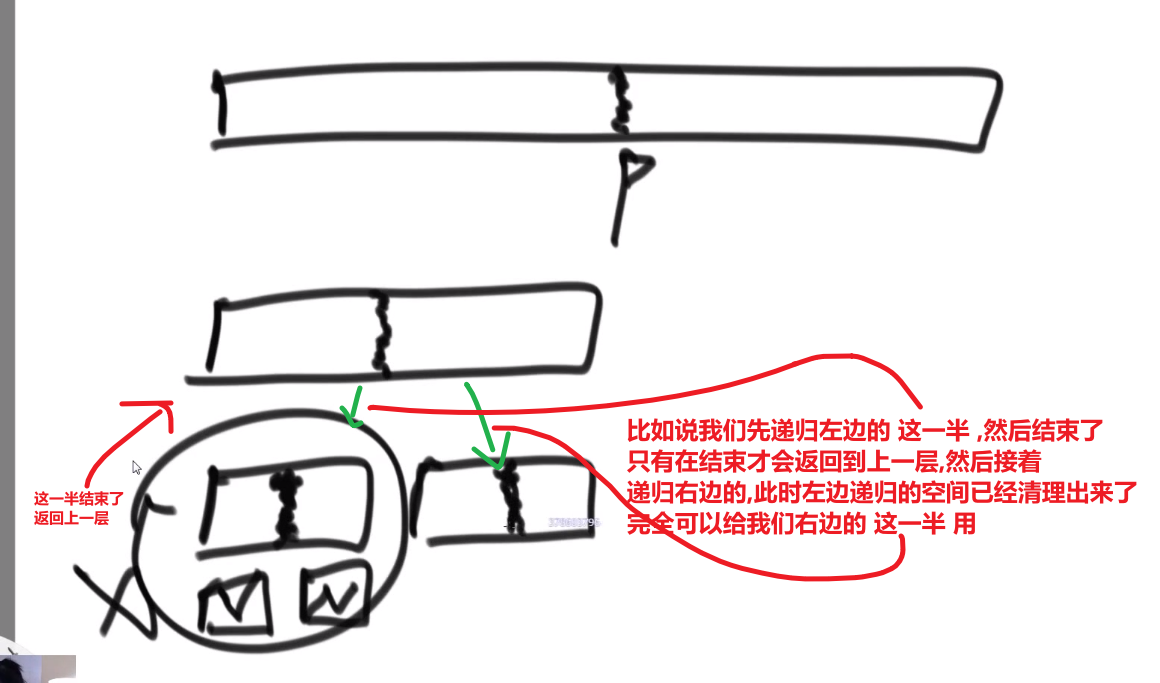
- 然后就 merge (需要一个 helper array 当工具人,然后需要考虑要是 merge 的某一边没清理干净,还有剩的)
空间复杂度就是那个 helper 数组,每次递归就会用到然后用完就没了会被垃圾回收器自动清理,注意这个并不是在递归里面产生的数组,那就不一样了,要是是在递归可能就不是 O (N) 空间复杂度了,merge 不是递归操作
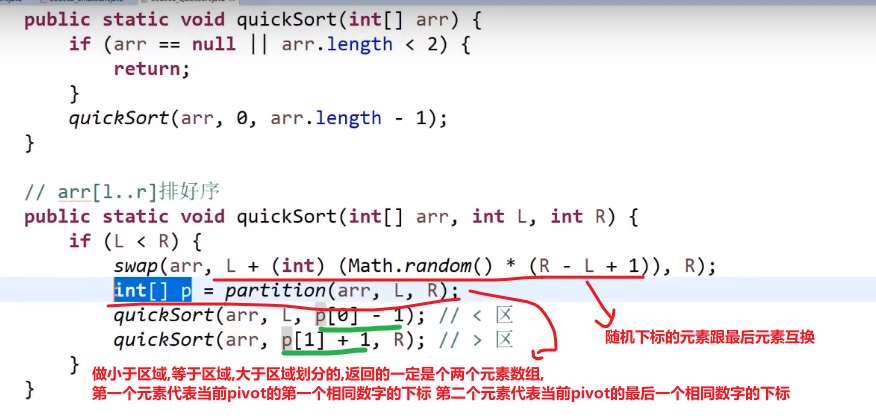
# 快速排序
快排 3.0 (1.0 和 2.0 参考别处,这里直接讲 3.0)
- 就是随机选一个数组中的数字把他放到数组最后面
- 接着让这个数字按照我们那个荷兰国旗问题解决方式一样,让小于这个数组放左边, 等于这个数字放中间,大于这个数字的放右边
- 然后把最后这个元素换到大于区域的当前 k 下标也就是大于区域第一个数,我们把这个数放到这就是可以让他和他一样的数 (如果有) 贴贴
- 接着直接调用自己递归,对当前的小于区域和当前的大于区域重复上面的操作,这就会让__每一个元素__他的左边就是比他小的,他的右边就是比他大的
我们这里使用荷兰国旗问题解决方式,那个等于区域就相当于如果有一些数字和当前数字一样,完全没有必要让他们在进行什么操作,直接拍一块,然后操作小于这个数的和大于这个数的就行了,就相当于一次可能处理了多个数,也有可能就处理了一个 (如果这个数字在这个数组里面是 unique 的)
注意如果不使用随机数字当做 pivot, 那么时间复杂度就是 O (N^2) 因为这个就是针对于 worst case, 所以要是固定选一个位置的当做 pivot 肯定他的 worst case 就是 O (N^2)
比如说固定从最后一个数当做 pivot:
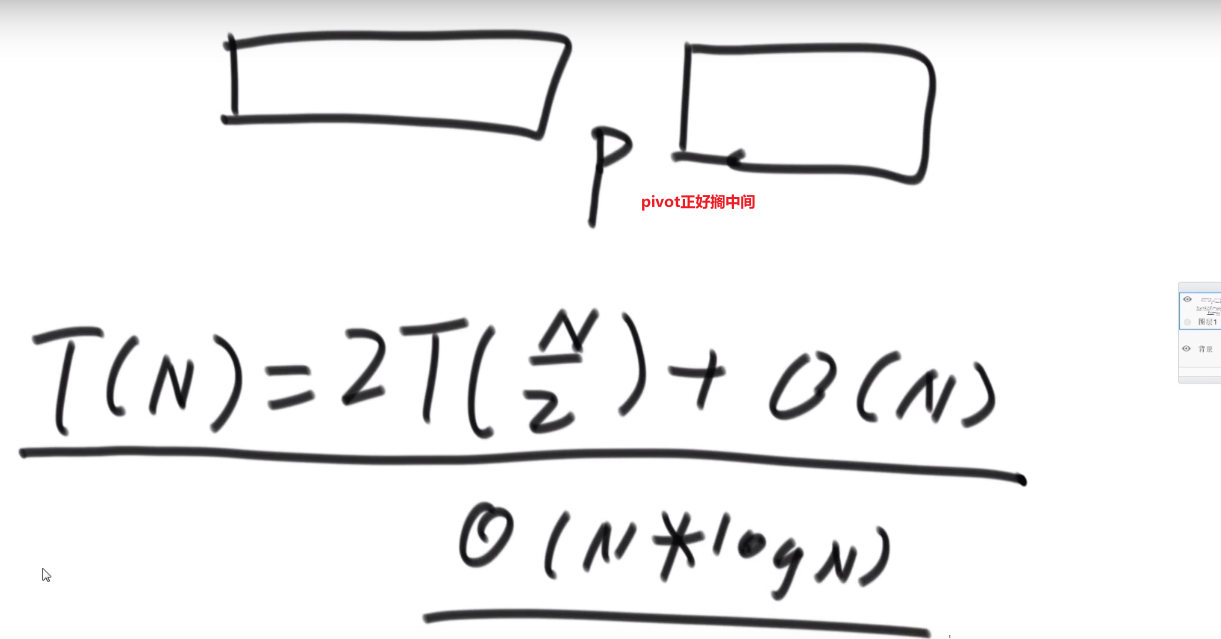
最好情况是
我们使用随机选的,都是概率事件,最后按照数学结论就是 O (Nlog (N)), 所以我们快排都是随机挑的 pivot (或者其他的等等等)
如果不是随机 (或者什么奇特的方法) 找 pivot 那么最差情况是 O (N)
如果好情况,或者就是随机也可以,那么空间复杂度就是 O (logN)
可以看到,就是类似于二叉树的展开
注意空间复杂度在递归的计算方法!!!这根我之前想的不太一样哈
可以理解为最大需要的额外的空间
我们是否可以使用非递归方式写快排,是不是可以省掉这个空间呢?不行!
这是因为我们快排实际的 partition 我们是不知道划分成什么样的,我们是跟实际状况的,有个小于区域,有一个等于区域,有个大于区域,就是因为我们这些数据状况 (到底每一层被划分成什么样子) 我们不知道,我们需要看实际状况,所以才需要记录这些区域的中点位置
就好比我们当前需要递归左边的小于区域,我们去执行压栈… 然后把小于区域执行完成了,我们返回到了这一层,我们此时需要递归右边的大于区域,但我们怎么知道这个大于区域到底是哪部分?当然是靠我们压栈保存这些中点信息,有了每一层的中点细,我们才可以按照那个中点信息 (那个下标), 来找到右边的大于区域然后递归他
所以就算自己写,自己写让他压栈,也照样是保存那个数据,所以那个空间是省不了的!
# 堆排序
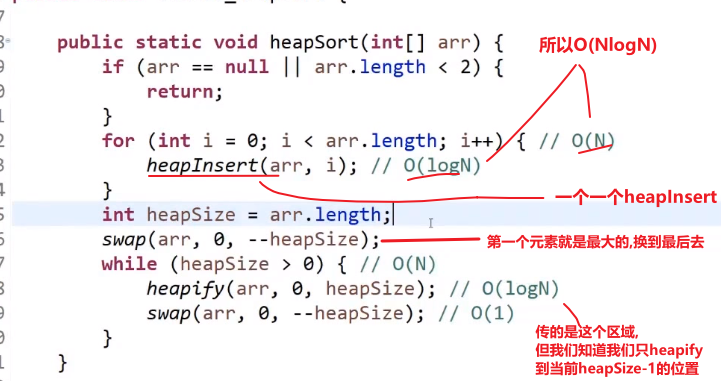
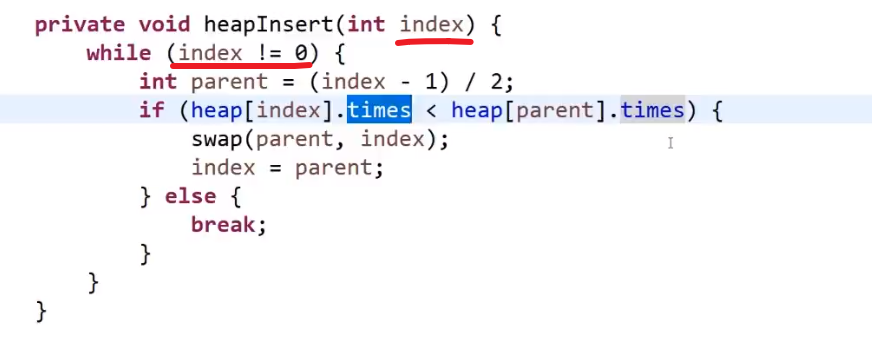
一个一个数字传进来的 heap insert
-
首先有数组,然后 heapSize 一开始是 0, 这个就是数组中现在几个数是我现在的堆
-
先接收第一个数字 (注意这样就是一个一个传的,而不是整个直接给你让你变成大根堆)
-
把那个数字放到我们 heapSize 现在的值的下标位置上,heapSize++, 现在我们数组中有一个数是我们的大根堆
-
接着把下一个数字放到 heapSize 现在的值的下标位置上,heapSize++
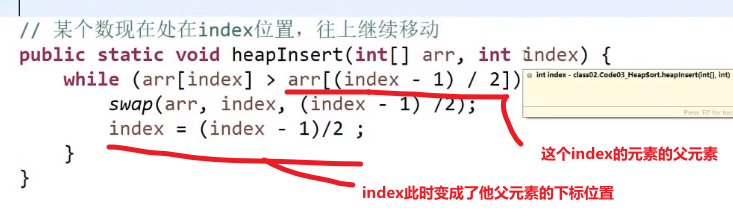
现在看这个放的数字的位置会是第一个的子孩子,所以要看现在还是不是大根堆,也就是当前数字有没有他父亲大 (他可以靠 (i-1)/2 下标算出他父亲的下标)
- 如果没有父亲大或者等于,那就直接下一个
- 如果有父亲大,那就 bubble up (注意要是比当前父亲大,然后互换了,需要继续比较看换了后比那个时候的父亲是不是更大,如果还是更大,那就需要继续换,这个就是 bubble up 或者 heap insert)
-
把一个一个传进来的数字都这么操作放入数组中,然后当结束时 heapSize==nums.length
-
我们已经有了一个大根堆结构
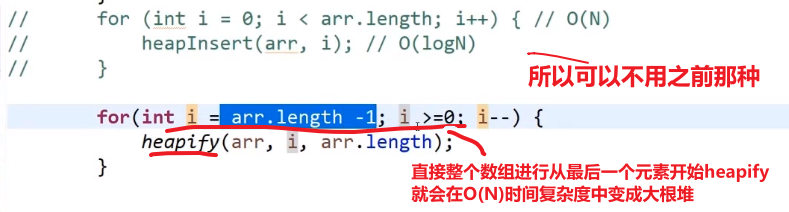
** 如果直接让我们对一个数组变成一个大根堆,而不是一个一个元素 heap insert, 用这个方式!!!**
修改我们的 heapSort 里面的方法,就是不用 heap insert, 而是从最后一个元素使用 heapify
使用这个这个更快!!!时间复杂度比一个一个 heap insert 更低 (虽然之后一个个元素放到正确位置然后进行 heapify 还是占大头 O (NlogN) 所以 overall 还是 O (NlogN) 时间复杂度)
其实这么做更好,比一个一个进行 heap insert 形成大根堆要更好,这是因为:
- 首先如果 N 个元素,那么差不多会有 N/2 个 leaf node, 每个 leaf node 进行 heapify 操作,因为他下面什么都没有,所以假设只是看了一眼,所以就是 1
- 如果 N 个元素,那么差不多会有 N/4 个倒数第二层的节点,每个那一层节点进行 heapify 操作,最多只是看一眼然后移动一步,所以就是 2
- 如果 N 个元素,那么差不多会有 N/8 个倒数第三层的节点,每个那一层节点进行 heapify 操作,最多只是看一眼然后移动一步然后再看一眼再移动一步,所以就是 3 (其实应该是 4, 但就差不多,这些大概理念)
所以整体复杂度:
我们可以解开:
__== 所以如果我们直接整个数组变成堆,而不是一个一个元素 heap insert (复杂度 O (NlogN)), 那么我们复杂度只需要 O (N) 了!!!==__
不过之后一个个元素放到正确位置然后进行 heapify 还是占大头 O (NlogN) 所以 overall 还是 O (NlogN) 时间复杂度
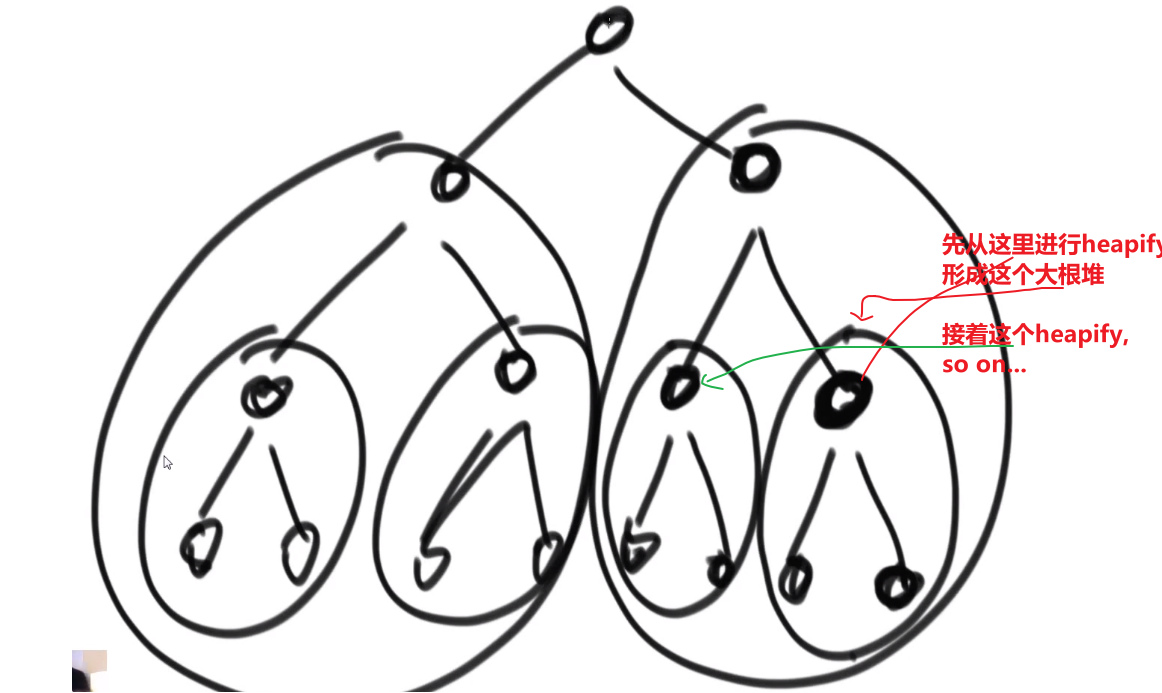
- 把每一个子树变成一个大根堆,这样子整个都会是个大根堆
其实从这个数组最后一个数字也就是,最后最右一个 leaf 出发开始 heapify 也可以!!!只不过那些 leaf 进行 heapify 都是不会动的
heapify
- 有了一个大根堆我们就可以从数组中取出第一个元素就是最大的元素,然后让剩下的进行 heapify 操作,再次形成大根堆,然后再取出第一个元素也就是我们所有的数据的第二个大的,so on…
- 不过我们也可以直接把第一个元素也就是最大的直接跟最后一个元素交换,heapSize–(此时 heapSize=nums.length-1, 没错就是这,不过我们知道我们接下来就不用管这最后一个元素了,因为已经在正确的位置上了)
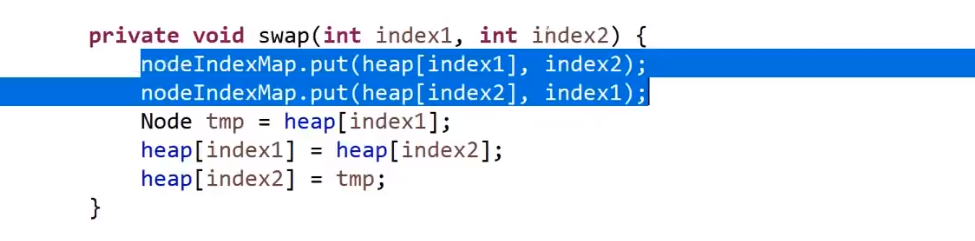
- 此时我们第一个元素是当初最后一个元素,我们可以使用 heapify 也就是 bubble down, 跟他的 左孩子和右孩子 (都是使用数组下标可以算出来的) 之间更大 的那个,如果比我们当前元素更小,那么交换,注意左孩子或者 == 左孩子和右孩子 (因为堆结构就是往左到右 fill 的,想想也合理,你数组如果有左孩子和右孩子,那么右孩子的下标就是左孩子的下一个,怎么可能会有 左孩子有右孩子没有 的情况)== 可能会是 null!!! 如果是 null 那就不换呗
- 我们就一直比,直到我们的元素比他此时的 左孩子和右孩子之间更大 的那个更大或者一样的话,那就不换了,到那就行了
- 此时我们就又形成了堆结构,接着把第一个元素也就是数组所有数第二大的放到 heapSize 现在的值 - 1 的下标位置,然后 heapSize–, so on…
- 直到我们的 heapSize 变成 0 代表数组所有的数我们都排序好了
注意在每次我们的把一个数放到了正确的地方后,我们的 heapSize 就成为了那个数的下标的位置,我们下次 heapify 操作只需要针对数组下标为 0 到 heapSize-1 位置就行了
问题:
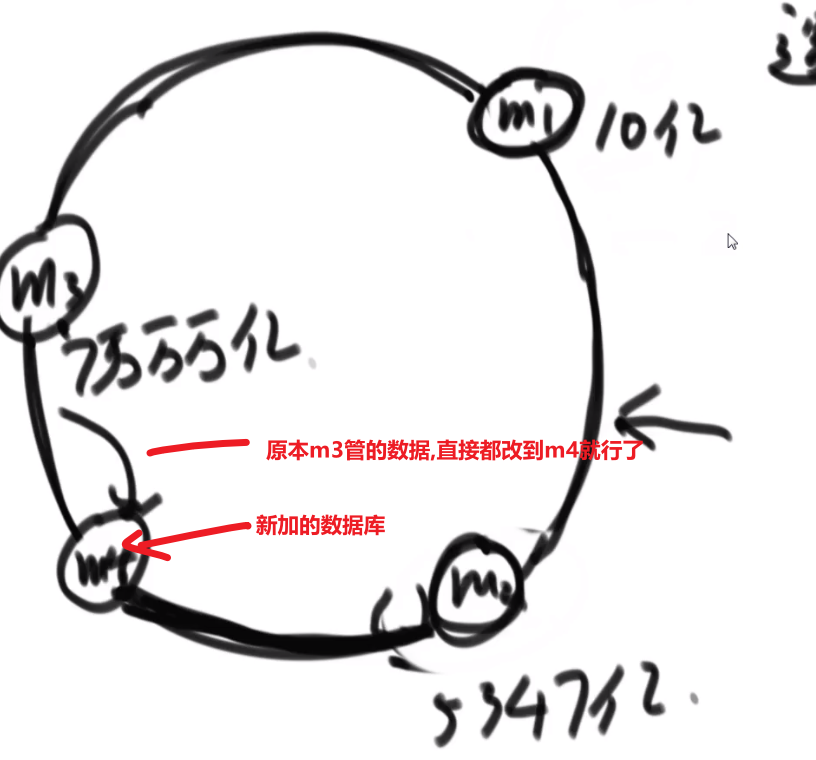
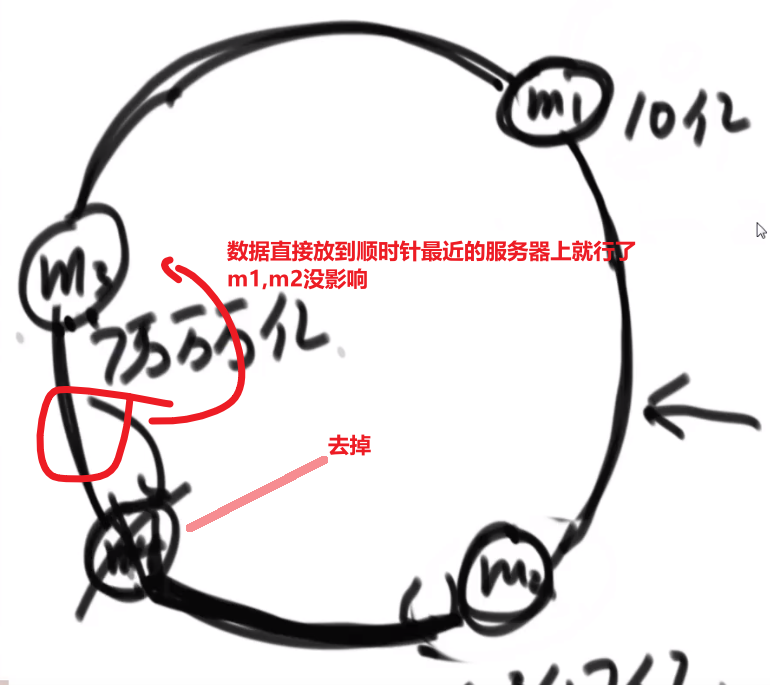
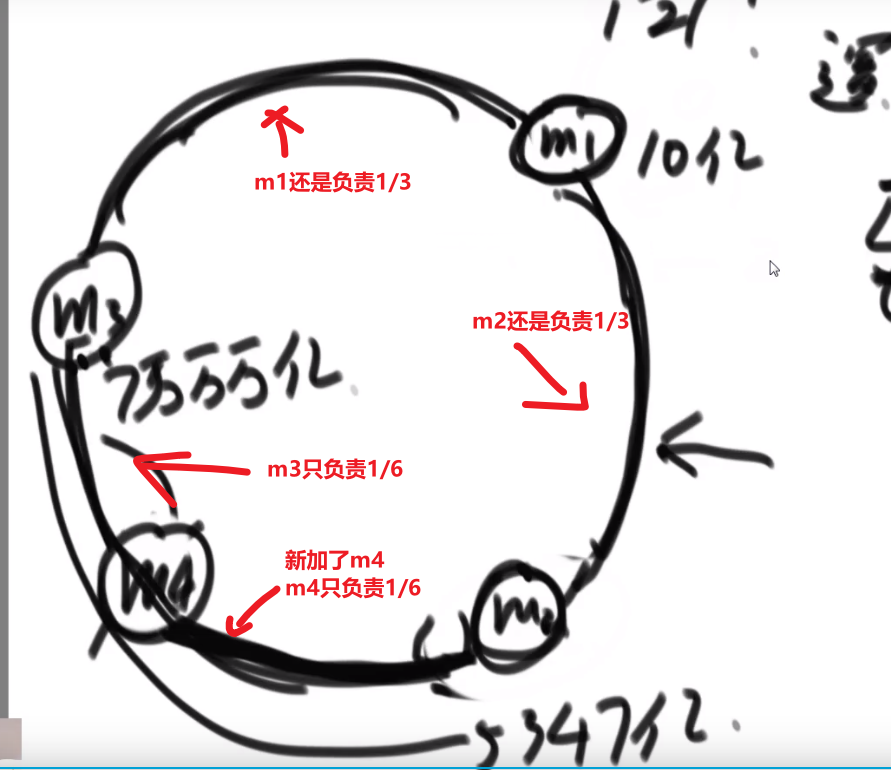
如果我们已经形成了一个大根堆,结果有人突然把大根堆里面的一个下标的数改了,我们再怎么形成堆?
- 我们可以__对这个下标的元素__调用一次 heapify, 调用一次 heap insert
- 这样如果这个数改小了,那么就会按照 heapify 到合适自己的位置上去,heap insert 不会起效果
- 这样如果这个数改大了,那么就会按照 heap insert 到合适自己的位置上去,heapify 不会起效果
时间复杂度
因为堆其实就是二叉树操作相当于了,所以你对于一个元素然后 heap insert (也可以不用) 或者 heapify, 其实就是二叉树的高度,也就是 logN 级别,最多只需要走一个高度就行了,其他不需要碰
所有的 N 元素,那么就就是 O (NlogN)
空间复杂度
**O(1)!!!**
因为 heapify 和 heap insert 只有用到有限几个变量
# 桶排序、计数排序、基数排序
计数排序
每次统计当前数有多少个,然后给对应的元素位置中的数字 + 1,下次输出时按元素中的个数输出。
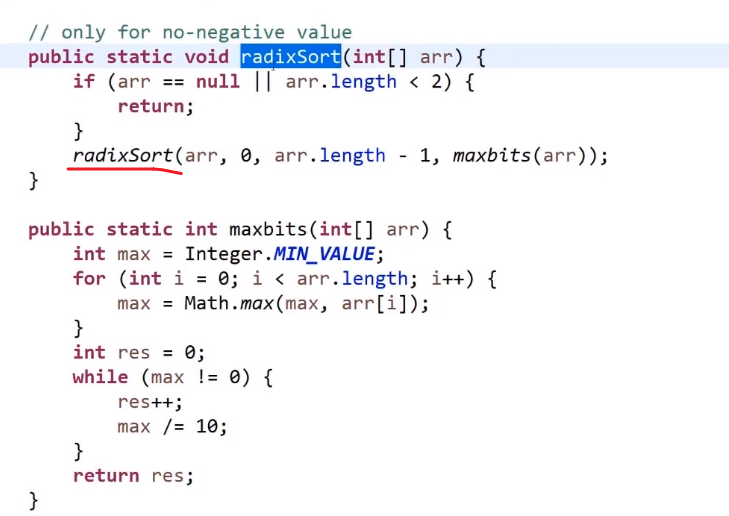
基数排序
比计数排序要好,因为没有那么麻烦创造那么多空间,只需要准备几个几个桶就行了,但是还是依然跟数据状况有关,排的东西还是需要是进制的,不然还是不行,不基于比较的排序都需要从数据状况搞点什么
- 非基于比较的排序,与被排序的样本的实际数据状况很有关系,所以实际中并不经常使用
- 时间复杂度 O (N),额外空间复杂度 O (N)
- 稳定的排序
时间复杂度、空间复杂度 均为 O (N),工程中不常用,但是笔试过程种可以使用这种办法来降低时间复杂度
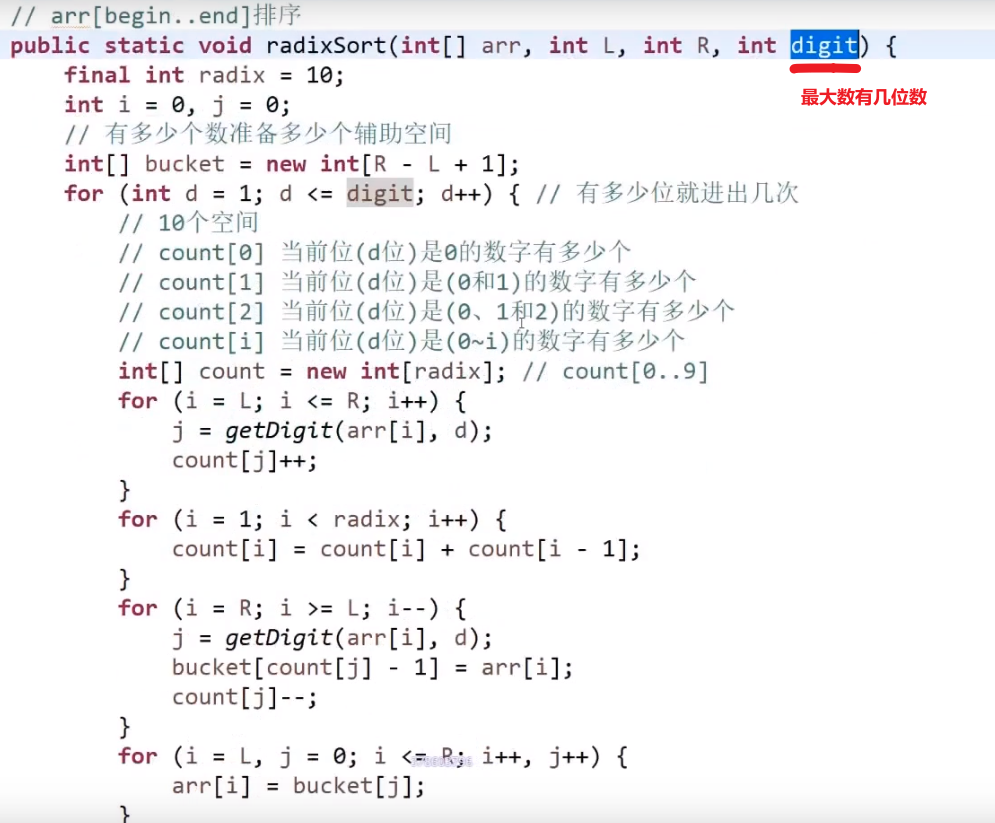
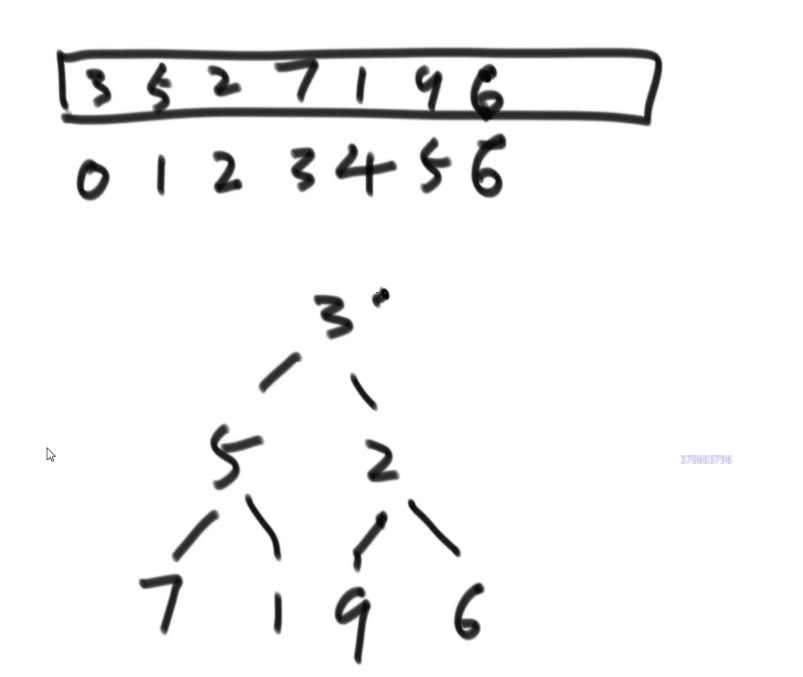
对于给定的排序范围的数,进行排序。需要排序的数有 n 个。准备 n+1 个桶。
遍历每个数,将每个数装到对应的桶之后。再从第一个桶中取出,依次输出。
桶,基数排序就是先个位排序再十位排序,最后就是百位,然后等等等
先把个位数的排了,然后十位… 优先级更高的之后再排,先把个位数的优先级给搞好,然后一层一层来,最后就是所有位数的都排好了
都是准备十个桶
十进制的数就 10 个桶,3 进制 3 个,2 进制 2 个…
属于不基于比较的排序,但是要求数字就是某种进制的才行
实际理论比较复杂!!!(这里代码没用桶而是词频表,看视频!https://www.bilibili.com/video/BV13g41157hK?p=4 大概 2:09:35 部分)— 很大的优化 -> 分片,然后出桶直接从右到左等等等
# 排序总结
不基于比较的排序,对样本数据有严格要求,不易改写
基于比较的排序,只要规定好两个样本怎么比大小就可以直接复用
基于比较的排序,时间复杂度的极限是 O (NlogN)
时间复杂度 O (NlogN)、额外空间复杂度__低于 O (N)__、且稳定的__基于比较的__排序是不存在的。
为了绝对的速度选快排、为了省空间选堆排、为了稳定性选归并
# 查找
# 二分
- 找出 mid position
- 看数组的 mid position 的元素跟我们要找的一不一样
- 可以使用
left + ((right - left) >> 1)防止溢出,移位也更高效
- 可以使用
- 要是要找的数字更大我们就去 mid+1 到 right 找回调自己继续找
- 要是要找的数字更小我们就去 left 到 mid-1 找回调自己继续找
- 所有操作要被
left < = right条件的 while 循环包括着,如果 left>right 说明- 比如说找到最后一个元素一比要是当前找的更大就往右找也就是 mid+1 到 right
- 因为当前是最后一个元素,说明 mid 算出来的就是他自己,此时要是 mid+1 然后还是那个 right 老值然后回调的话,收到的 left 就会比 right 更大,此时我们 return -1 说明二分到最后一个元素也不符合,所以没有要找的
- 比如说找到最后一个元素一比要是当前找的更小就往左找也就是 left 到 mid-1
- 因为当前是最后一个元素,说明 mid 算出来的就是他自己,此时要是 mid-1 然后还是那个 left 老值然后回调的话,收到的 right 就会比 left 更小,此时我们 return -1 说明二分到最后一个元素也不符合,所以没有要找的
- 比如说找到最后一个元素一比要是当前找的更大就往右找也就是 mid+1 到 right
/* 注意:题目保证数组不为空,且 n 大于等于 1 ,以下问题默认相同 */
int BinarySearch(int array[], int n, int value)
{
int left = 0;
int right = n - 1;
// 如果这里是 int right = n 的话,那么下面有两处地方需要修改,以保证一一对应:
// 1、下面循环的条件则是 while(left < right)
// 2、循环内当 array[middle] > value 的时候,right = middle
while (left <= right) // 循环条件,适时而变
{
int middle = left + ((right - left) >> 1); // 防止溢出,移位也更高效。同时,每次循环都需要更新。
if (array[middle] > value)
right = middle - 1;
else if (array[middle] < value)
left = middle + 1;
else
return middle;
// 可能会有读者认为刚开始时就要判断相等,但毕竟数组中不相等的情况更多
// 如果每次循环都判断一下是否相等,将耗费时间
}
return -1;
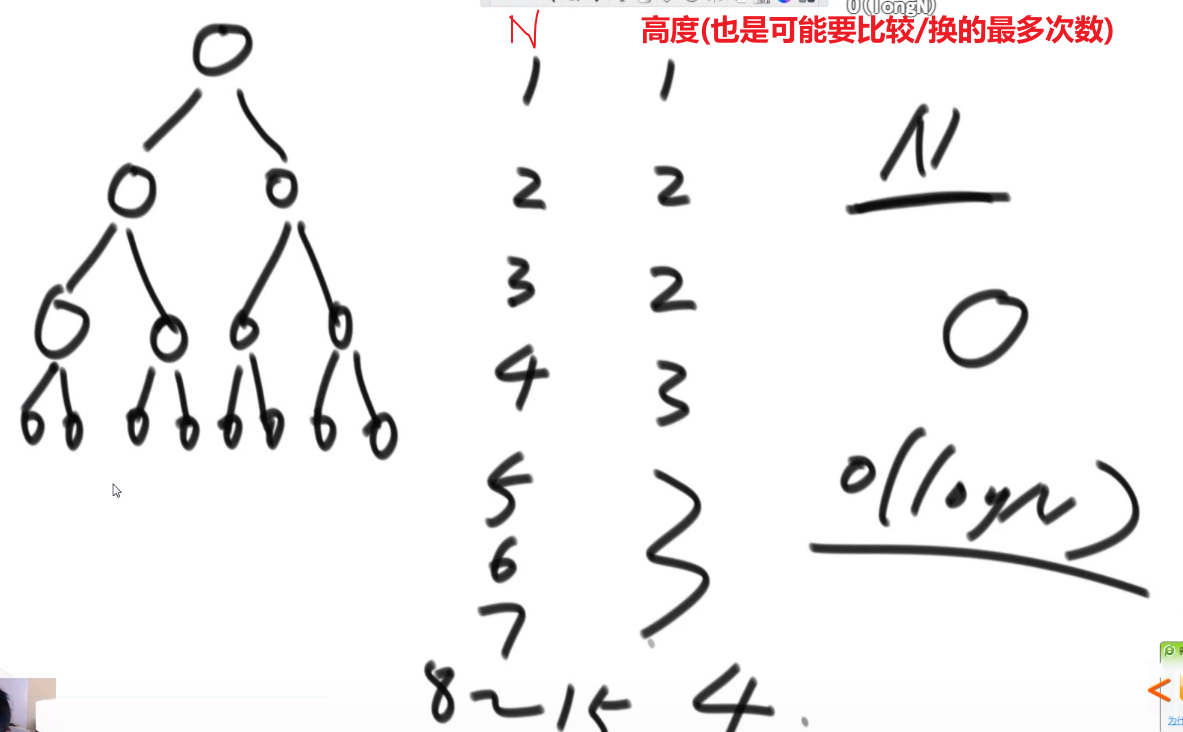
}O (logN)-> 因为比如说 N=16, 那最多要看 4 次,而 24=16, 所以 log16=4, 所以 logN = 最多要看的次数
一般是用于已经有序的数组但这不代表无序就不可以用了!!!
比如说数组中无序,邻近数字不相等,想找出任意一个局部最小的数字 -> 局部最小指的是比左右元素 (如果有) 都要小的数字,也可以用二分查找,肯定会找到一个的,这比暴力 O (N) in this case 更快
主要看情况,看适不适合
# 一些数据结构
# 堆
其实就是完全二叉树的结构,或者就是从左到右开始满的二叉树
用数组对应一个完全二叉树 (好像只是堆我们这么做,反正最上面 (数组第一个下标) 的放着我们最大的 / 最小的元素 -> 大根堆,小根堆)
这样因为是使用数组方式存的节点,所有对于每个下标为 i 的元素
- 他的左孩子,如果不是 null, 就会在 i*2+1 下标
- 他的右孩子,如果不是 null, 就会在 i*2+2 下标
- 他的父亲,就会在 (i-1)/2 下标 —> 如果是 root 也就是下标为 0 的,那么 (0-1)/2 照样还是 0, 还是他自己
# 链表
记住如果链表带有换头操作,那么返回值设为 head, 返回的就是最终答案的 head (好像和这个还有助于递归算什么东西)
# 优先级队列和 java 的 Priority Queue
- 优先级队列底层就是堆结构,堆顶就是优先级最大的
- Java 里面的是 Priority Queue, 如果放的是数字,那么默认就是小根堆结构
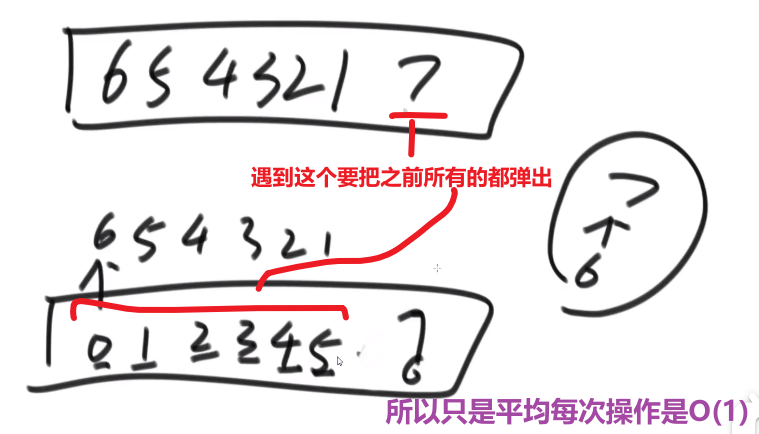
这个底部是数组模拟二叉树的堆结构,所以会有时候加多了,需要扩容,扩容好像就是当前大小 x2, 然后把旧数组里面的拷贝到新建的大数组里面到对应的位置
一共加了 N 个数,经历了 logN 次,因为:
比如说 N=16
- 我们加了两个数超了一下,扩容
- 我们加了四个数超了一下,扩容
- 我们加了八个数超了一下,扩容
- 我们加了 16 个数超了一下,扩容
总共扩容了四次,也就是 logN 级别的 (log16=4)
而我们每次扩容的代价是 O (N) 时间复杂度的,所以所有的操作就会 O (NlogN), 也就是我们添加了 N 个元素的总代价就是 O (NlogN)
而我们想要的是平均下来,每添加一个数,会是多少时间复杂度,也就是
O(NlogN)÷N, 也就是平均下来, 每添加一个元素,即便考虑了扩容问题,也就是 O (logN) 的时间复杂度
所以扩容这个事,并不会影响__比如说让我们使用堆排序__最终的表现,以为我们每个元素的添加 /poll 形成的堆是 O (logN) 的时间复杂度的,这个扩容也是 O (logN) 的时间复杂度,所以并不会怎么影响我们 overall 时间复杂度的计算的
这个是人家 java 底层帮我们维持的堆结构,我们无法对堆结构里面的某一个元素进行改变然后 expecting it to 再次形成堆结构所以这个相当于是个不好的地方,我们自己创造堆结构的话可能会更 flexible 想改哪个改哪个,只不过之后自己要给那个调用 heapify 和 heap insert 让整个结构再次变成想要的堆结构
他就是个黑盒,你给他一个又一个,他可以按照结构给你一个又一个,你无法直接改变黑盒里面的东西,就算可以改也会是代价比较高的 (因为要扫描每一个找到那个被改的,然后进行各种操作变回堆结构)
# 哈希表 (hashMap,hashSet)
java 的 hashMap 和 hashSet 底层就是哈希表实现的
- hashmap/hashset 增删改查任何操作不管数据以及有了多少,都是常数操作 O (1), 比较大的常数 (比数组直接寻址要大得多)
- treemap/treeset (有序表) 增删改查任何操作不管数据以及有了多少,都是 O (log (n))
- 注意要是往 treemap/treeset 里面放复杂数据类型或者自己定义的各种类型,需要你提供一个比较器,按照你定的规则来排序
有序表!
# 二叉树以及各种 (先中后序) 递归,非递归遍历
二叉树的先序、中序、后序遍历
先序: 任何子树的处理顺序都是,先头节点、再左子树、然后右子树
中序: 任何子树的处理顺序都是,先左子树、再头节点、然后右子树
后序: 任何子树的处理顺序都是,先左子树、再右子树、然后头节点
# 递归序
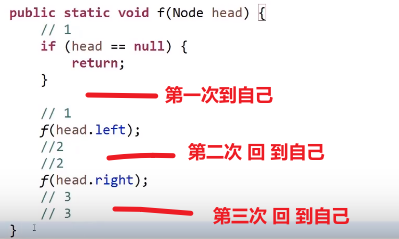
每个结点都会经过三次
递归序:
前序,第一次到达当前节点就打印
中序,第二次到达当前节点就打印
后序,第三次到达当前节点就打印
# 非递归遍历
# 前序遍历
准备一个栈,
-
第一步__将非空根结点压栈__
出栈并打印
-
先将刚刚那个出栈的节点的非空右子树结点压栈 (空了就不压呗)
-
后将刚刚那个出栈的节点的非空左子树结点压栈 (空了就不压呗)
还是先序,只不过非递归方式就是我们自己放入栈,要先把右边的压进去,再把左边的压进去
当前栈顶的节点出栈并打印
- 重复 2,3
直到栈空了,说明所有的都出栈了 (这里出站顺序就是前序,我们可以做各种操作), 所有的都出栈了就一定是在所有节点 (每次循环栈 pop 出来的) 左孩子都已经压栈然后出栈或者就是空的,所有右孩子也都已经压栈然后出栈或者就是空的
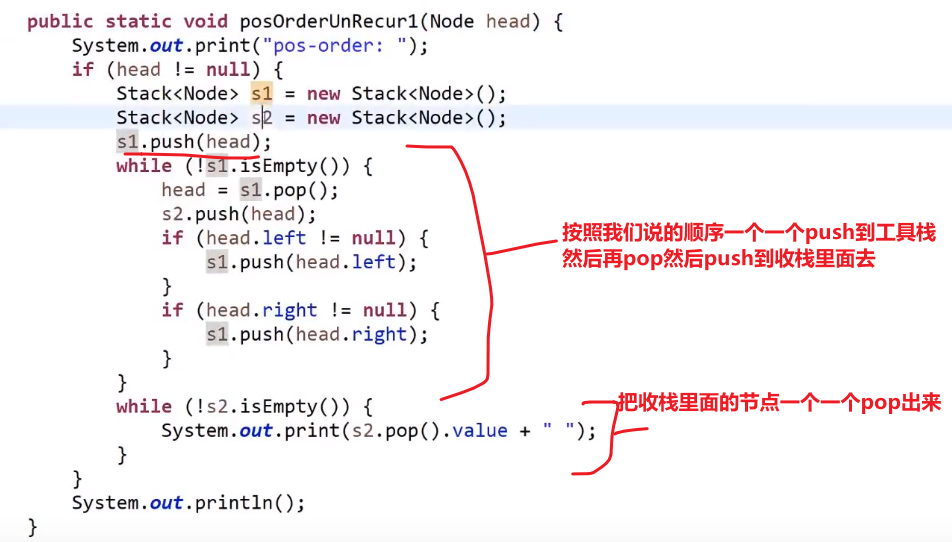
# 后序遍历
两个栈,一个工具栈,一个收栈
- 第一步__将非空根结点压栈__
出这个栈,入收栈
-
先将刚刚那个出栈的节点的非空左子树结点压栈 (空了就不压呗), 注意这里又是左边先了
-
后将刚刚那个出栈的节点的非空右子树结点压栈 (空了就不压呗)
出这个栈 (此时就是我们上面刚放的那个右孩子节点 (注意如果是空的话就不是这个了)), 入收栈
- 重复 2,3
最后收栈的样子就是:
此时再将收栈的节点一个一个 pop 出,那么最后的顺序就是后续了!
可以这么理解:
- 我们压入工具栈又取出的顺序就是 --> 头 右 左 (因为先压入然后先 pop 的头,然后先压入左边的又压入的右边的,然后 pop 的是先 pop 右边的再 pop 左边的)
- 把这个顺序一个一个压入收栈里面就是想要逆序呗 --> 左 右 头 (__先压入头,再压入左,再压入右,所以最后取出的顺序就是 左 右 头 __也就是后序了!)
# 中序遍历
- 第一步__将非空根结点压栈__
- 将当前栈里面的节点的左节点压栈,一直重复直到当前栈顶的那个节点没有左节点了
第一次执行第二步

- pop, 打印 pop 出来的,再讲 pop 出来的右节点 **(如果不是空,如果没有右节点就不用管了,继续 pop 下一个栈顶然后打印然后看有没有右节点等等等)** 给压入栈中,然后对这个右节点 (可能代表的子树) 做第二步
这就做到了让头先入栈,接着左边再入栈一直入到底,然后弹出左的 (因为此时弹出左的肯定是 leaf, 没有右节点), 我们就会回到对于那个弹出的左节点是头节点,然后这个会再弹出,然后看有没有右节点有的话就压栈,此时这个右节点又会去看自己有没有左节点压栈的,有的话就重复我们上面的 steps, 没有的话就弹出来, 所以我们最终打印 (或者可以在弹栈进行操作的顺序为–> 左中右,就是中续!!!). 对于每一个子树来说都是左头右的顺序
都是任何树先做再头,然后对于右边的先做再头,so on…
我们当前完全反过来,按照右边的为主,那么就会是右头左顺序了, 看自己什么需求
# 二叉树的深度优先遍历
其实就是二叉树的先序遍历,就同一回事
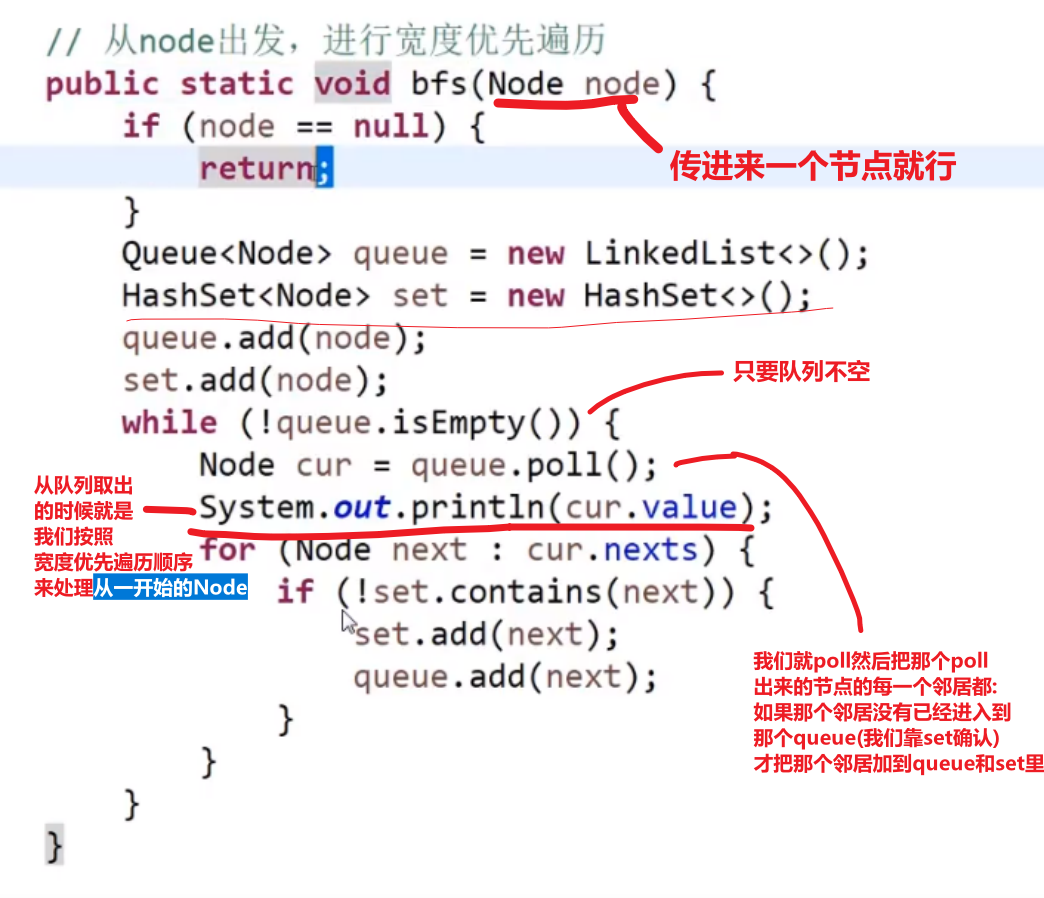
# 二叉树的宽度优先遍历
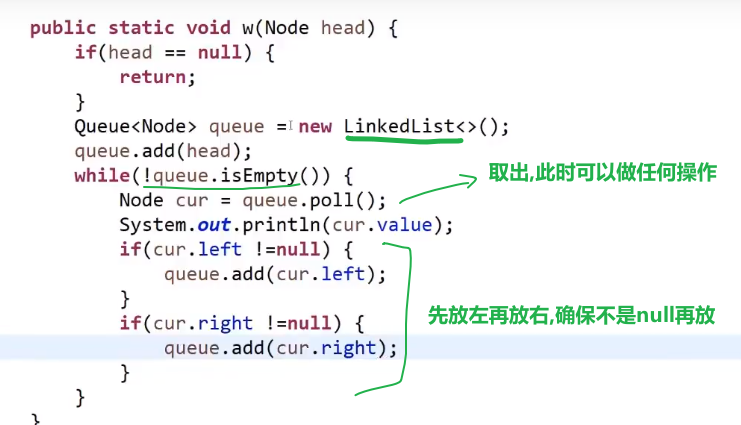
== 宽度遍历用队列!!!== 先进先出
-
首先头节点进去队列
然后出列,此时打印或者各种操作…
-
让当前出列的左节点 (如果有) 先入列
-
再让当前出列的右节点 (如果有) 再入列
然后出列,此时打印或者各种操作…
- 重复 2,3
就是按照宽度来的,一层一层打印
java 里面 linkedList 就是双链表,双链表可以做队列的 (也可以用来做 stack, 看你用什么方法了), 所以可以直接用 linkedList 当队列用
# 图
adjacency list
adjacency matrix
(直接带 weight 的)
矩阵中每一个值是按照 edge 来考虑的,有没有 direct edge (两个点直接就有一个 edge 而不是比如说 B 导向 C 然后 C 导向 D)
其实图的代表方式很多,甚至可以用一个数组来代表
我们可以对一种数据结构做所有图的算法,然后之后面试要是给我们不同数据结构代表的图,我们只需要 process 那个转化成我们想要的数据结构,然后传进去我们之前已经会的模板,就可以了
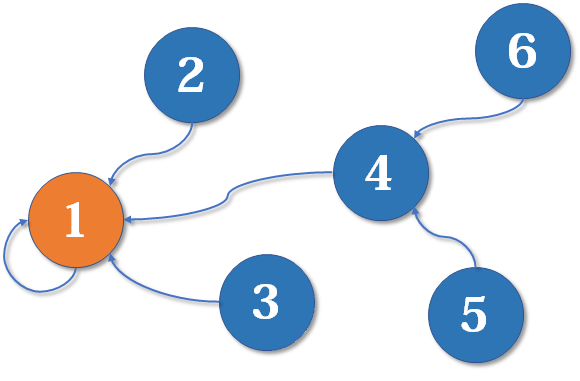
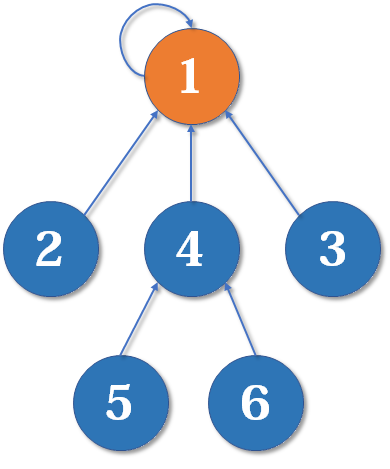
左神用的:
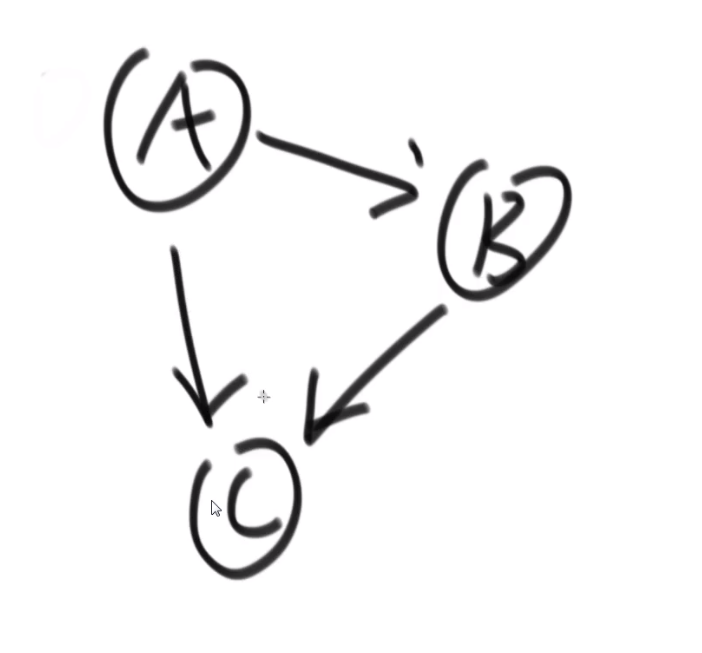
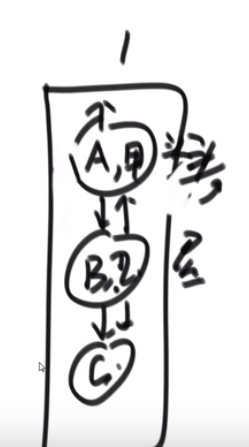
比如说这个
- A 的 nexts 是 B 和 C
- B 的 nexts 是 C
- C 的 nexts 是 null
也就是我们当前这个节点属于我们自己的 edge 而且是往外指向的节点
我们那个节点存的 edge 属性则是那个当前节点往外指的所有 edges 本身,并不是那些 edges 指向的节点
只要管 digraph 就足以,因为我们 graph 其实就是两面的 directed edges 互相指 (you get what i mean)
然后就是我们上面说到的接口函数转换成我们想要的结构:
左神的这种数据结构支持所有的 (大部分的) 算法
如果有哪个算法并不需要某些值,比如说不需要 Nodes 的 nexts 属性什么的,那么直接不用设了那个就好了
只把我们需要的设置好,我们就可以使用这个结构弄那个算法,复杂度不会提高很高
图跟二叉树不一样,可能有环,所以遍历要考虑这个,不要陷入死循环
注意下面这个只是针对于这个 graph 里面连着的节点,要是那个节点没有连,或者是对于 digraph, 然后他的 in 是 0 我们还不从那个节点出发,也会忽略掉那个节点
# 图的宽度优先遍历
# 图的广度优先遍历
注意用栈然后这种方式,有一刻会让所有的节点都会存在于栈中,然后之后他们因为还没空所以还是会挨个 pop, 也就是反序了
不过不管我们事,看需求吧大部分。反正我们处理一个节点是那个节点加入到 set (第一次加入到 stack 里面去 (可能会被重复加入好几次)) 就处理。就是别忘了一开始的头节点一开始加入到 set/stack 也是需要处理
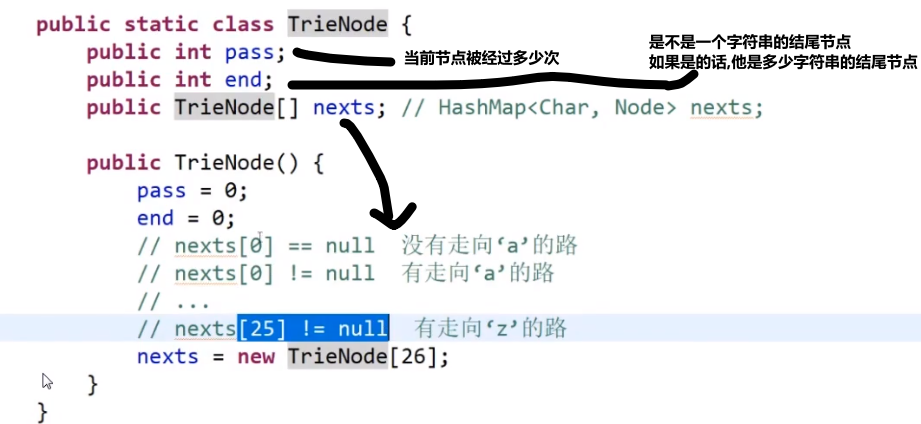
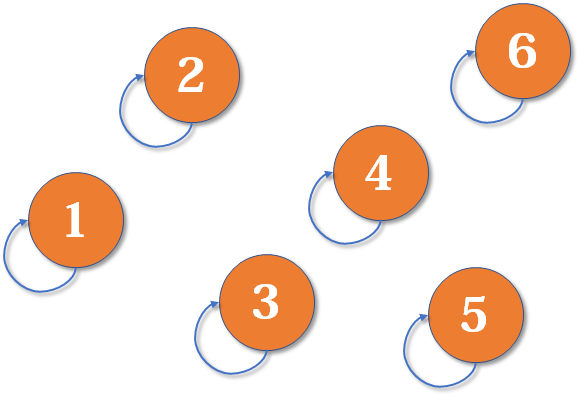
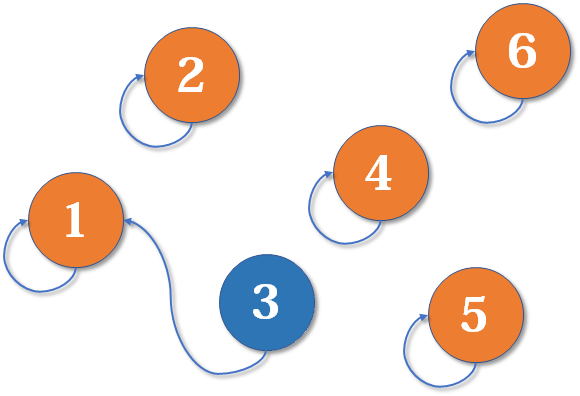
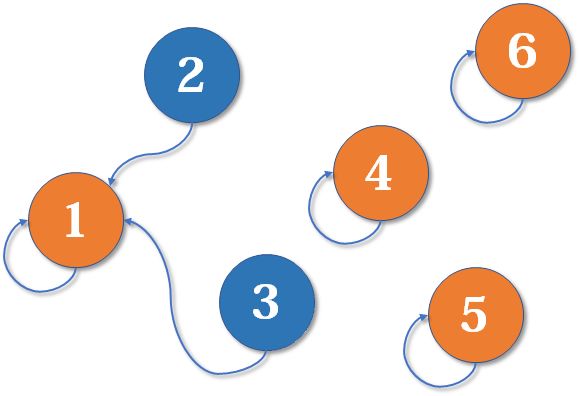
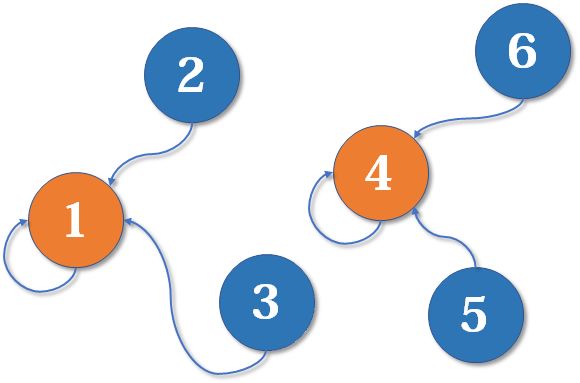
# 前缀树
首先我们可以把数组中存的字符串挨个来看
- 一般是用字符放到 edge 上然后 toNode 指向一个不是 null 的,也就是指向一个节点就行 (不过要是想把字符放到节点上也可以)
- 没有字符的道路那就建一个,如果有就复用等等等
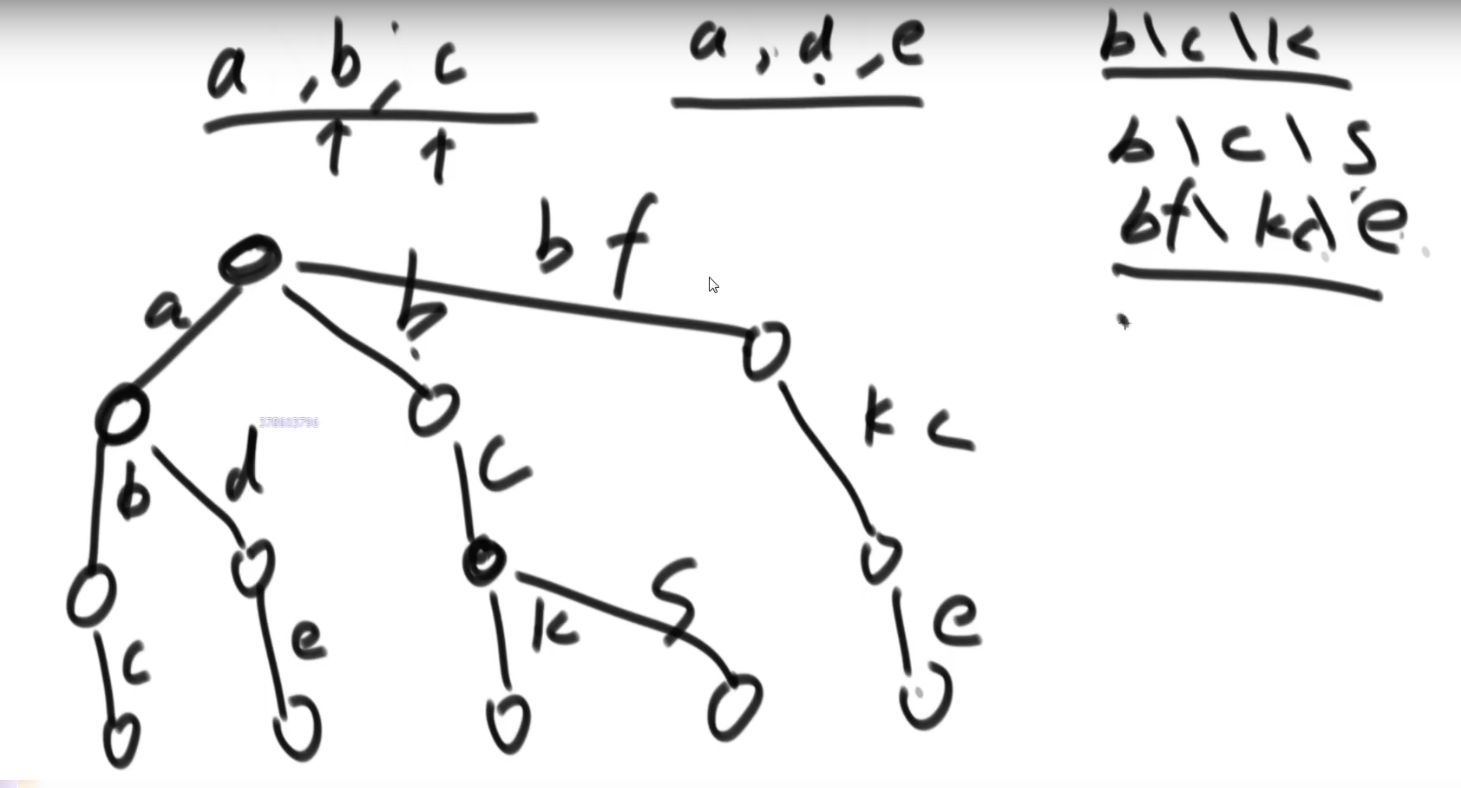
看以下数组形成的前缀树

我们其实可以对那些节点做些自定义,让他存一些我们想要他存的信息
比如说
- 一开始头节点,算是经过 pass 是 1,end 是 0,nexts 是一个数组,数组每个下标都是指向 null
- 接下来有了个 a 字符,我们看有没有 a 的路也就是我们头节点的 nexts 的下标为 0 指向的是不是 null
- 发现是 null 就会让那个改成不是 null-> 而是让下标指向我们新建的一个节点
- 然后我们这个新建的节点就会是 pass 是 1 (p++ 了),end 是 0, 然后处理 b 等等…
…
- 到了最后 c 处理完了生成了一个新节点,发现当前这个字符串结束,那么就让我们这个新建的节点的 end++ 此时就是变成 1 (要是之后还有字符串最后在这节点结束,那么继续加加等等等)
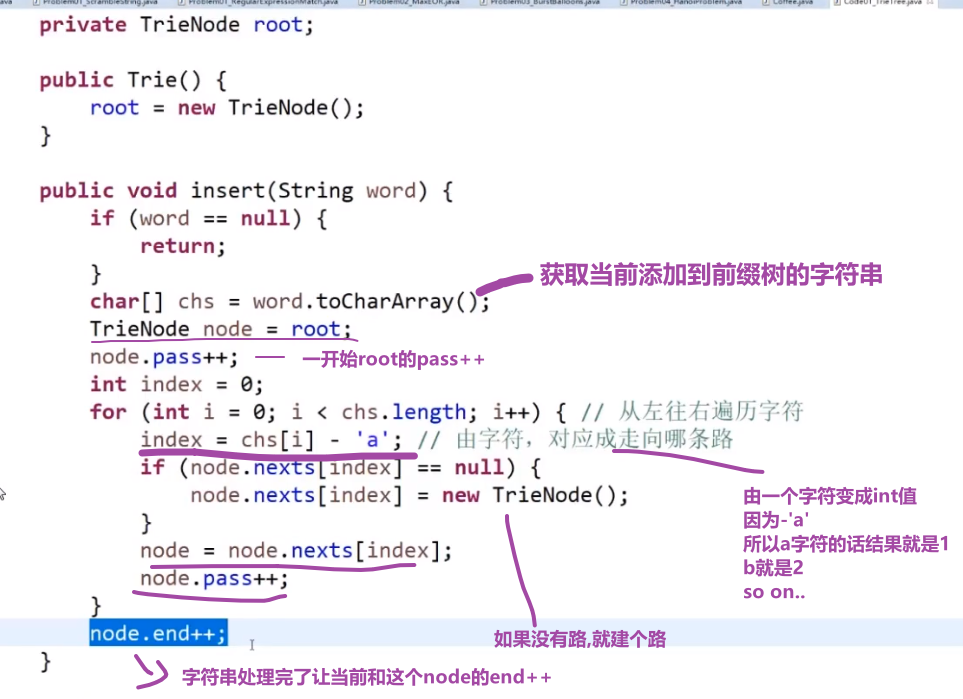
比如说一堆字符串,最后会是这样:

此时比如说我们想要查这些里面有没有 "bc" 这个字符串
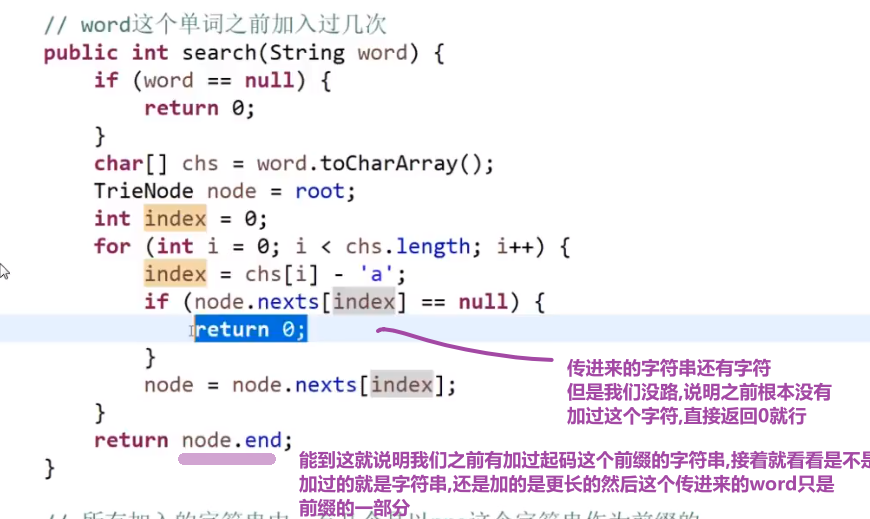
- 我们先按照上面的方式让他一个一个走 (不要改值啊!我们之前已经把前缀树建好了,我们只是找一个字符串在不在而已), 走 b 然后走 c 然后那个 c 指向的节点再看那个节点的 end 值是不是 0, 如果是 0 说明你之前加的字符换都没有 "ab", 要是等于 x (不等于 0), 那就一定意味着之前已经加了 x 次这个字符串
我们这样做代价很低,我们只要把一个前缀树建好了,然后再去找一个字符在不在我们的那个数组或者等等等里面 (which we took as input and made a 前缀树 for it), 他的代价只是查找的字符串的字符的数量,只要从头结点出发走过字符这个数量的距离就可以确定这个事
你会发现这还不如用哈希表,还方便,其实这个前缀树还有更厉害的用处
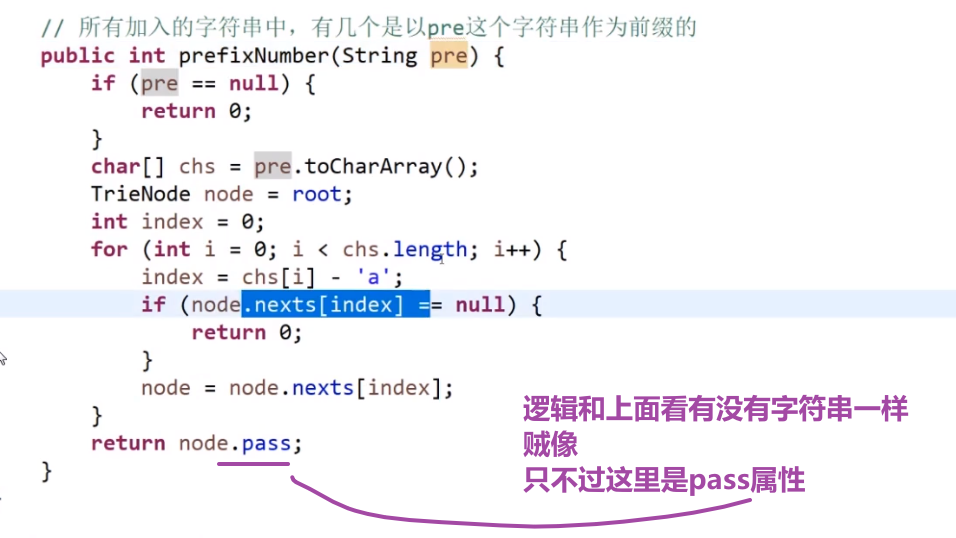
比如说:你想要找你之前加过的字符串,有多少个字符串是有 ab 作为前缀的?
- 我们可以先从头节点出发,然后看有没有 a 的道,有的话就走
- 接着看有没有 b 的道有的话就走,走到的这个节点他的 pass 值就是我们之前所有加过的字符串前缀为 ab 的数量

注意头节点的 pass 属性就是当前前缀树存的字符串是以 ""(空字符串) 作为前缀的
这个哈希表就做不到,而我们的前缀树可以做到
要是我们想要的不只是针对于 letters, 比如说任何可能的字符,那么我们可能需要一个一个 hashmap 来存 (nexts 属性) 信息,key 作为那个路 (也就是那个字符),value 作为那个路指向的节点,这样我们就不需要用数组 (元素一多就没法子了), 如果需要有序的还可以 treemap 等等等,都可以
搜索前缀树有没有一个字符串,如果有的话,有几个:
搜索前缀树有没有一个字符串作为前缀,如果有的话,有几个:
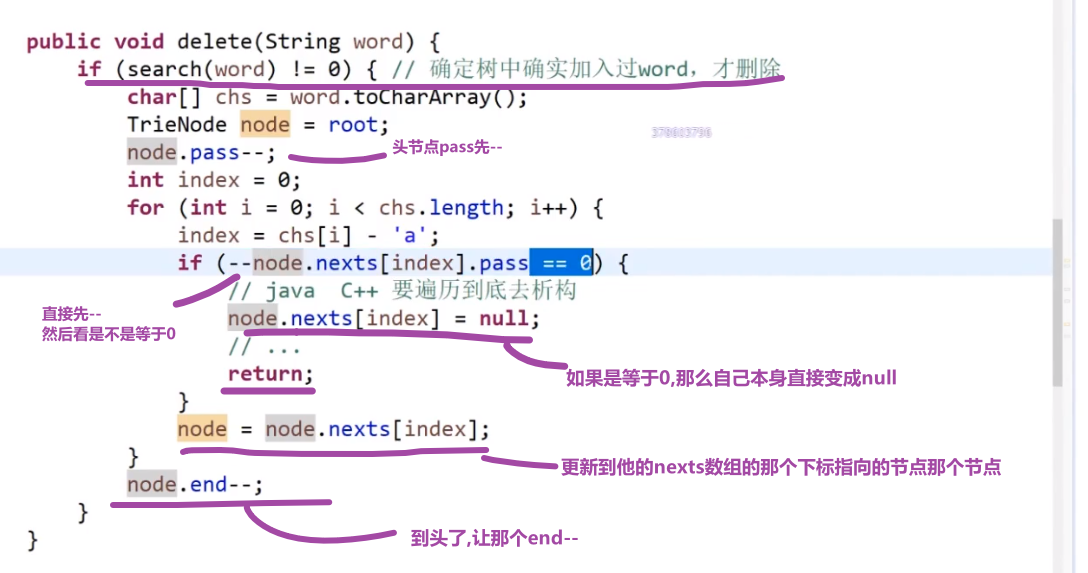
删除前缀树中的存的所有字符串的其中一个:
- 我们先看我们前缀树确实是有那个字符串 (用上面的那个方法看看返回值是不是不等于 0)
- 有的话我们再删,从头一个一个开始看,经过的节点都让 pass 值–, 然后让最后这个字符串结尾的那个节点的 end 值–就行了
如果我们删除的时候到了一个节点然后把他的 p 值–, 结果 p 变成了 0, 那么说明这个节点需要删掉,也就是上面那个的 nexts 数组里面的某个下标指向这个节点的指针应该指向 null 了,因为这个节点现在因为我们删除了那个字符串,导致了他的 pass 是 0 了说明就已经不会有任何字符串是通过他那里的,就算他后面还有节点,也都一样,不会有经过的了.
# Master 公式
# 排序,数组等问题
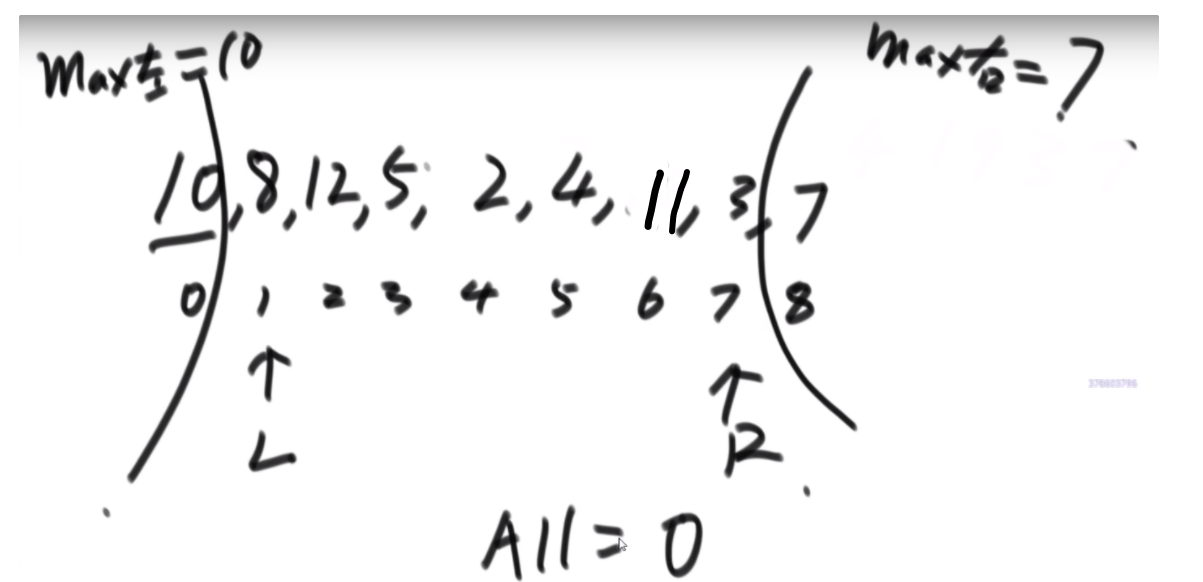
# 找出数组范围最大值
- O (logN) 时间复杂度 -> 用 master 公式
# 小和问题
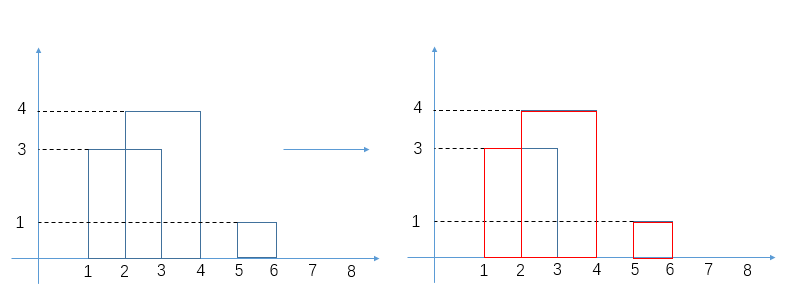
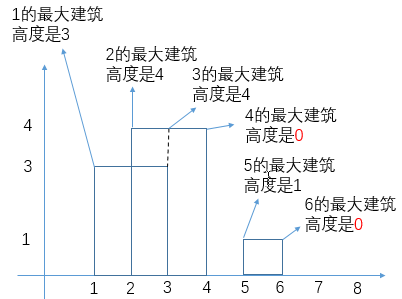
就是你遍历数组,所有在当前元素左边且要比当前元素的数字相加就是当前元素的小和,算出每个元素的小和然后把他们相加
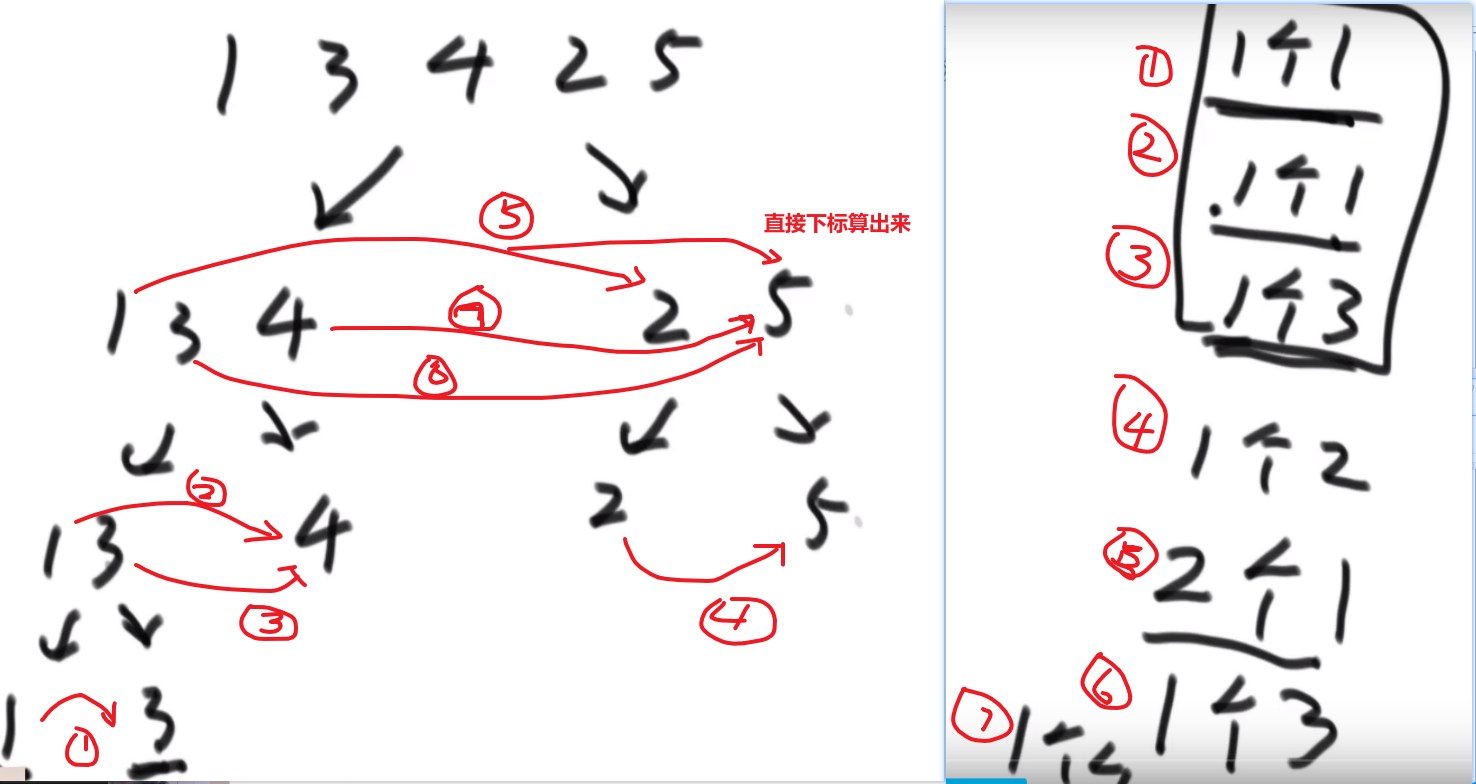
整个数组的小和,在这例子里面是 0+1+4+1+10=16
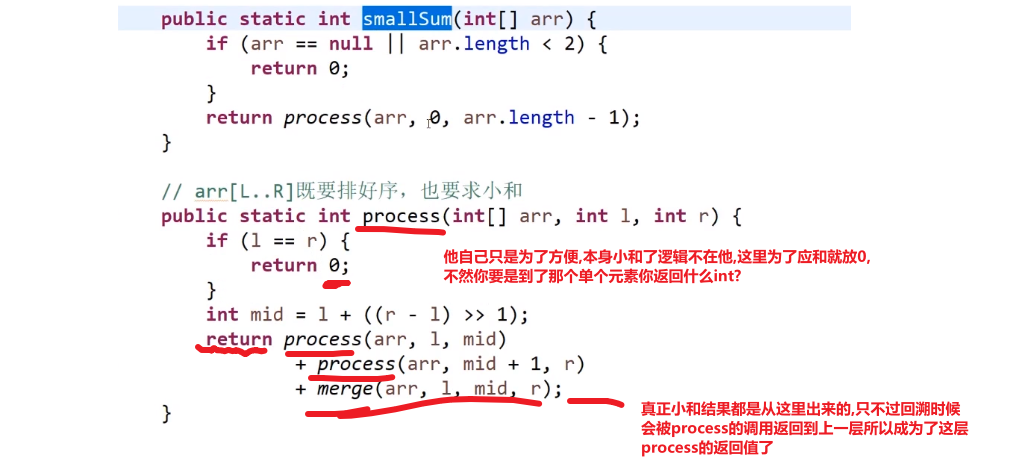
这个我们可以在使用归并排序的同时,多做些操作,计算出来答案
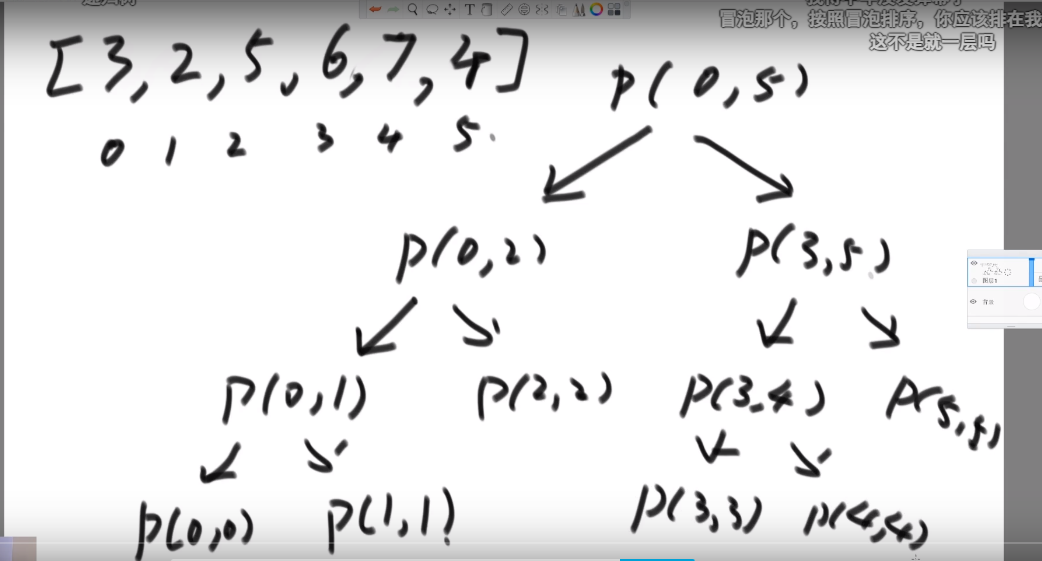
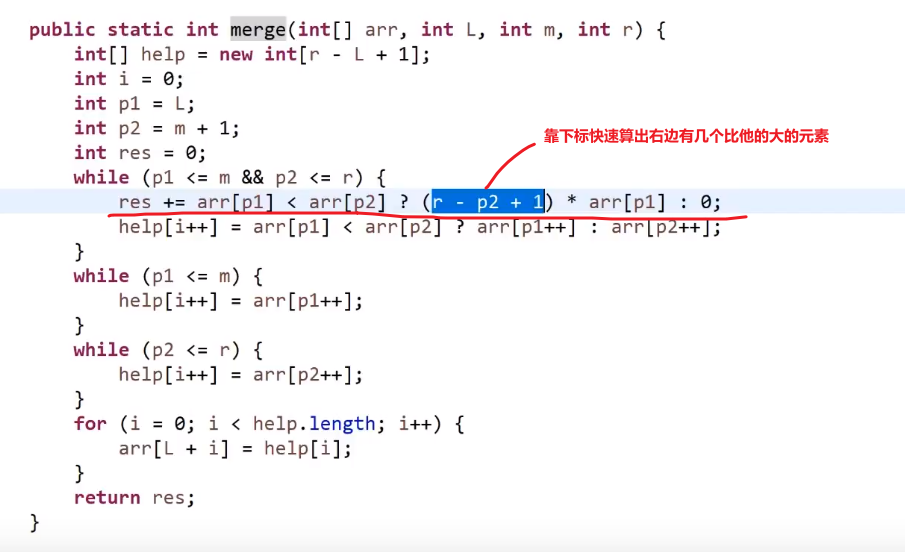
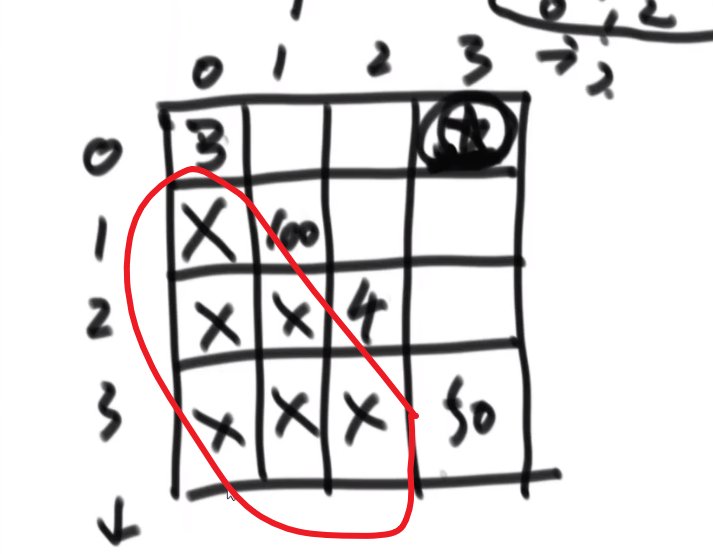
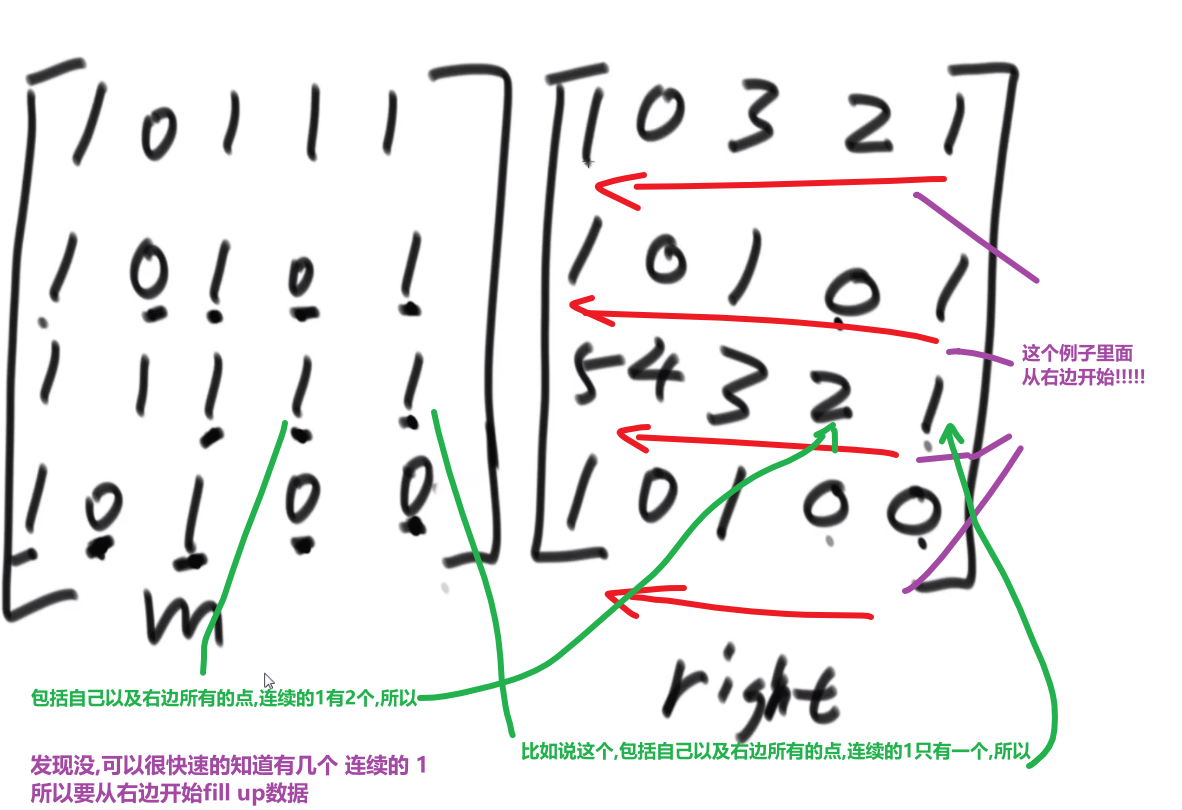
我们换种想法,每个元素,他的右边有几个比自己大,比如说上面例子
- 第一个元素是 1, 然后看右边有 4 个元素比自己大,所以我们需要 4 个 1
- 第二个元素是 3, 然后看右边有 2 个元素比自己大,所以我们需要 2 个 3
- 第三个元素是 4, 然后看右边有 1 个元素比自己大,所以我们需要 1 个 4
- 第四个元素是 2, 然后看右边有 1 个元素比自己大,所以我们需要 1 个 2
- 第五个元素是 5, 然后看右边有 0 个元素,所以我们需要 0 个 5
所以最后 4*1 + 2*3 + 1*4 + 1*2 = 16, 所以一样的
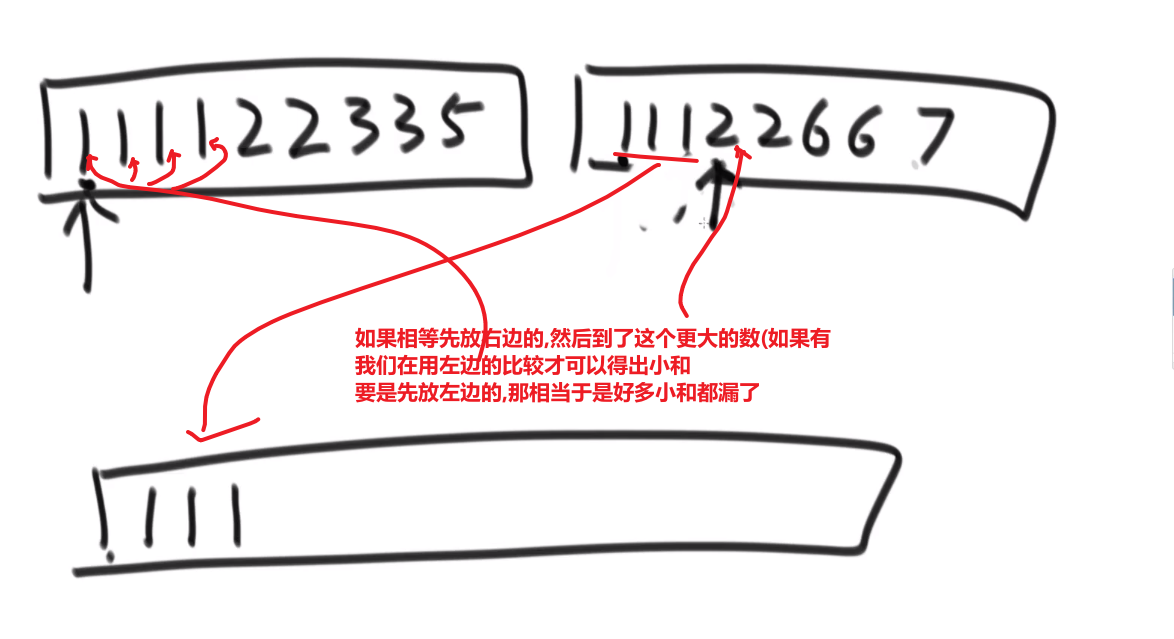
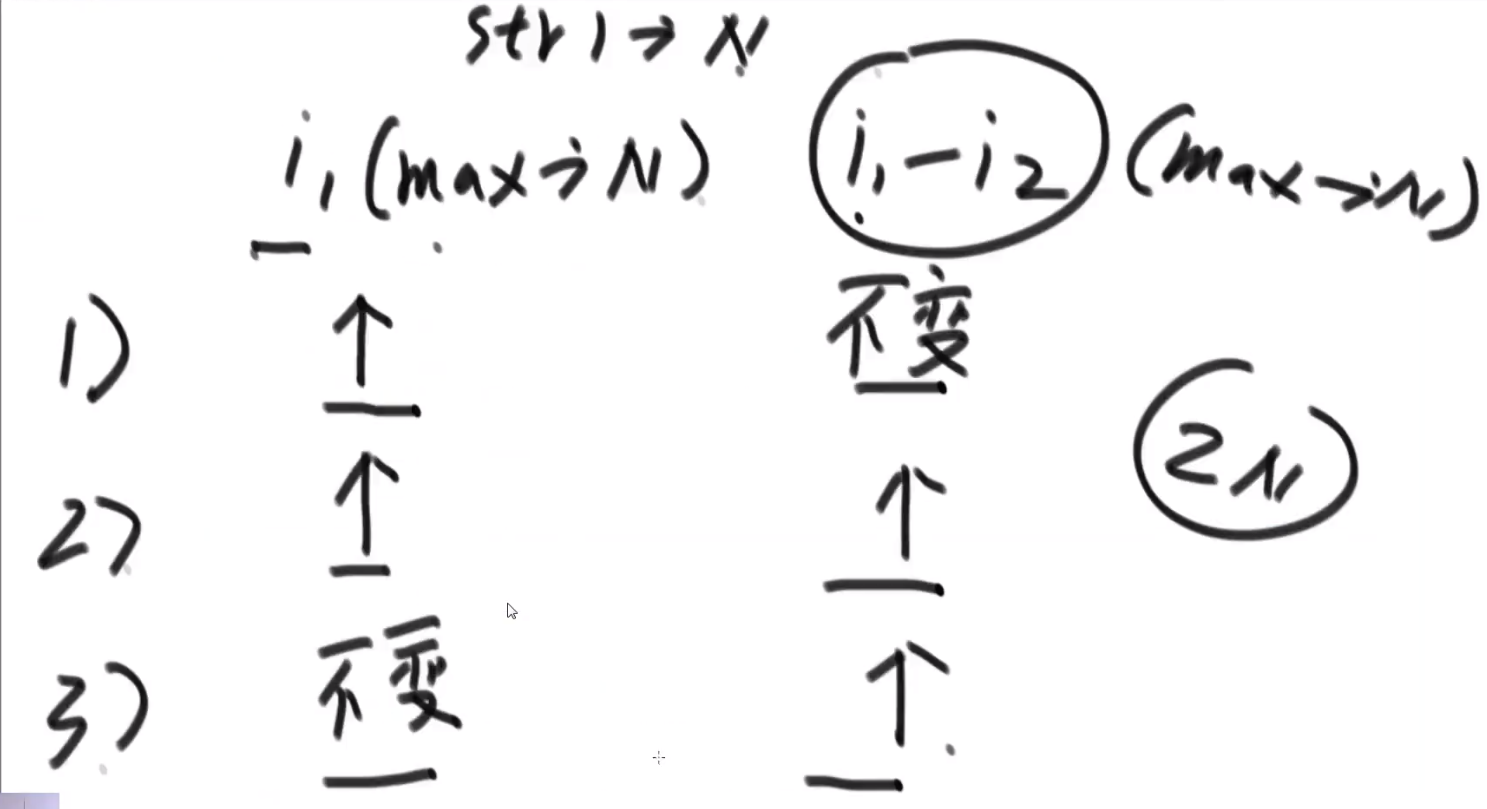
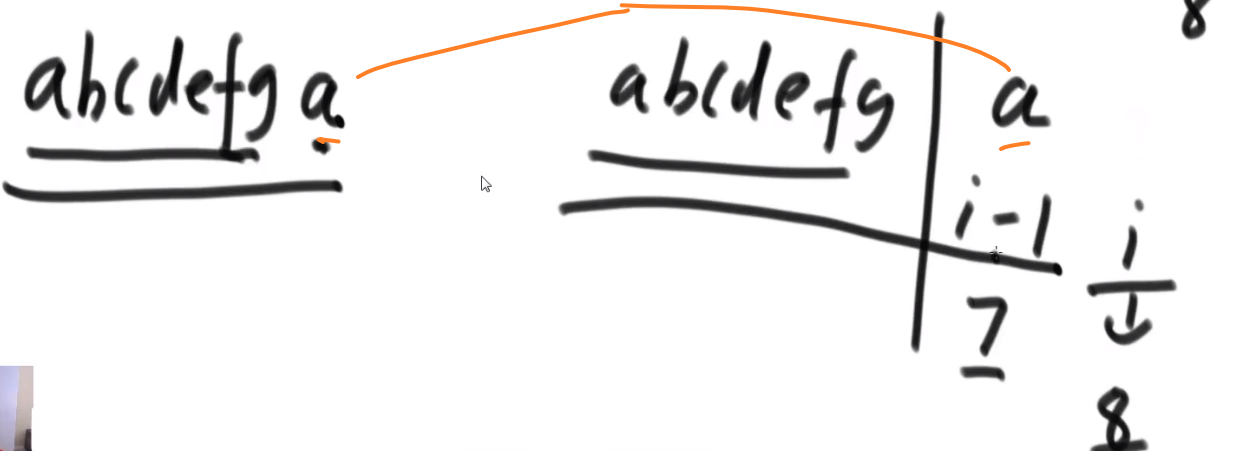
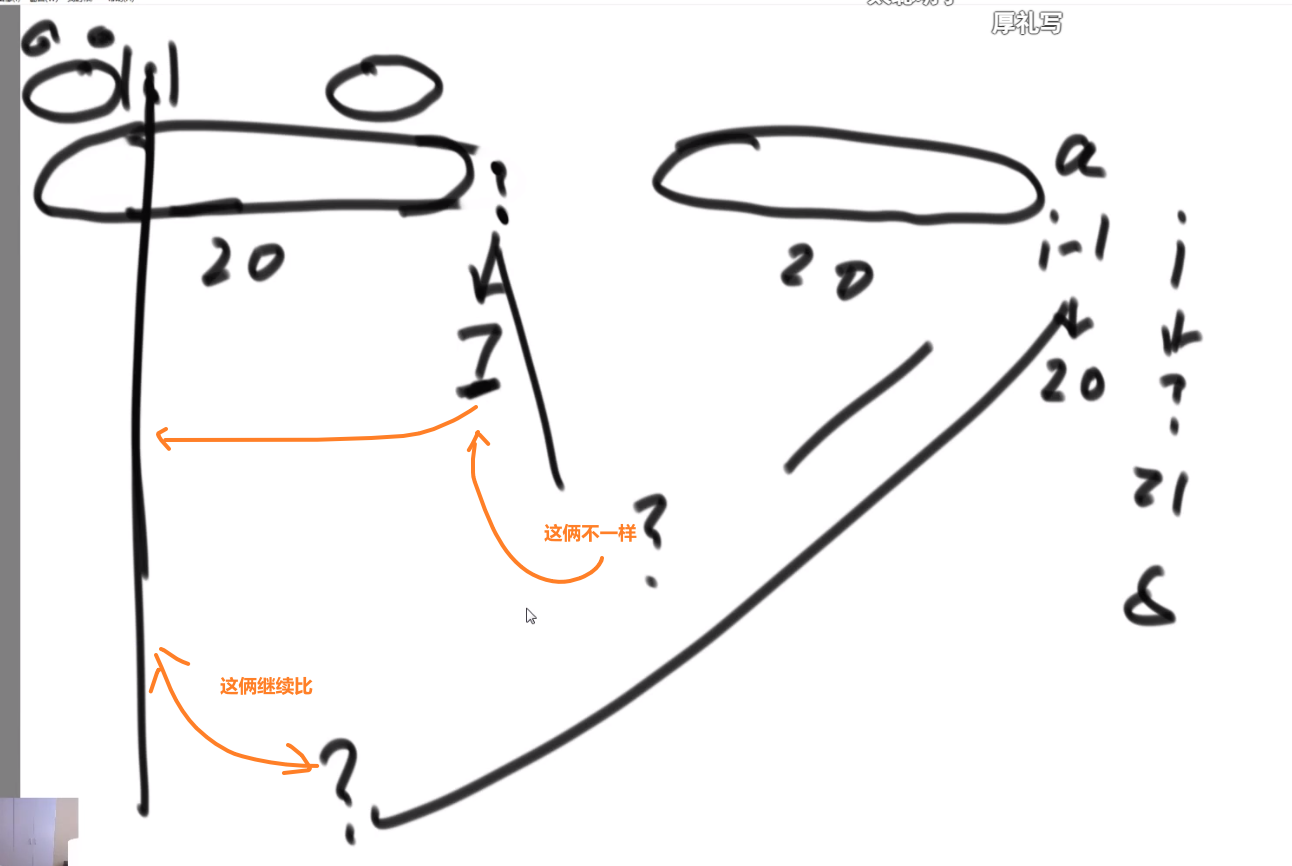
所以每次 merge 执行的时候,如果左边的要比右边的___要小___(注意 等于 不算!) 的话,就代表产生了小和,也就是当前左边这个值. 如果右边的这个数组是多个元素,那如果右边第一个比当前左边的这个元素要大,右边数组后面所有的元素都大,我们可以用右边数组下标快速地 (其实这个就是更快的原因,直接就找到了多少个元素更大,而不是一个一个比) 计算出有多少个比他大的然后小和值就增加比他大的那个靠下标快速算出来的数量 * 当前左边这个更小的值
== 但是注意!!!这个 merge 过程跟我们之前的 merge 过程有点不一样 ==
在这里, 我们如果左边和右边数组当前数是相等的,我们不会先放左边的,而是先放右边的
注意,正因为我们这里如果相等是先放了右边的,我们破坏了 merge sort 的稳定性,merge sort 在 O (logN) 的比较排序里面最有特色的就是他的稳定性,其他的都不怎么样 (比如说空间复杂度是 O (N), 是 O (logN) 的比较排序里面最大的)
当然需要本身的排序也是实实在在的需要的,要是不排序那就不对了,比如说右组必须是排序的我们才可以用下标快速的算出有多少个比元素更大的 ->(下标快速算就是 O (1) 啊)
每个小和都是没有遗漏的,分批的,没有重复的
- 不遗漏 -> 因为 merge 过程中,是一定会把某一个数右侧范围扩到一个整体的
- 不重复 -> 因为已经变成一个部分的东西,在这个东西内部是不重复产生小和的,只是左组跟右组 merge 的过程中,因为左组的数比右组的小,才会产生小和,所以不重算
因为这个差不多就是 merge sort, 所以时间复杂度就是 O (NlogN)
# 逆序队问题
比如说:
[3,2,4,5,0] -> 3,0 是个逆序队 3,2 是个逆序队 4,0 是个逆序队 etc…
计算总共有多少个逆序队
使用归并排序
- 每次 merge 我们都看,左边当前元素是不是比右边的要大
- 如果大,直接用下标方式快速算出多少个大的
- 如果小__或者等于__, 就直接左边的这个,然后看左边的下一个元素进行比较,…
不难看出,跟小和问题贼像,只不过反过来了,而且没那么复杂了
** 多想想像这种类似于 combination 的题,他问的不是 combination 哈,反正总是试试看 merge sort 能不能行,merge sort 就是可以快速找出左边和右边的某种区别 (一般是大于,小于这些的), 然后要是我们平常需要一个一个比,但是因为 merge sort 确保每次 merge 两边都已经是有序的,我们可以非常迅速靠着下标算出有多个匹配的!!!**
# 荷兰国旗问题
很简单
- 遍历我们数组,下标 i 一开始是 0
- 有个小于区域和大于区域 (如果只想要小于一个数的在左边,其他随便就不需要大于区域,大于区域是为了把大于那个数的放到右边,这样既有小于区域和大于区域,那么如果有和那个数一样的,那么会出现在中间左右的位置)
- 如果当前元素 <那个数,把当前元素跟小于区域下一个元素互换,小于区域往前走一步 (用下标比如说 j++),i++
- 如果当前元素 = 那个数,直接跳过让 i++
- 如果当前元素 > 那个数,把当前元素跟大于区域上一个元素互换,大于区域往前走一步 (用下标比如说 k–),i__不变!__
- 当 i 和 k 的值一样了,说明都处理完了,结束,完成!
如果只想要小于等于的放在左边,大于的放到右边的规则:
- 如果当前元素 <= 那个数,把当前元素跟小于等于区域下一个元素互换,小于等于区域往前走一步 (用下标比如说 j++),i++
- 如果当前元素 > 那个数,直接跳过让 i++
这就跟双指针一样的
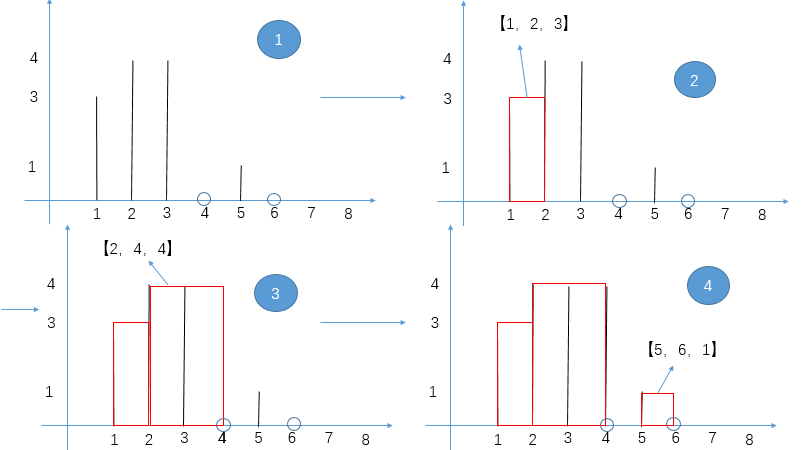
# 排序一个几乎有序的数组
** 使用堆排序!!!**
- 首先我们有个数组,然后一个 k 值
- 我们首先把下标从 0 到 k 的所有数字放到一个小根堆 (这里使用小根堆是为了方便,因为我们取的就是从 0 下标开始的一些数字) 里面,这样我们就有了这个范围的小根堆,我们知道数组最小的数字肯定是在这里,因为最多不会超过 k, 不会出现在超过那个范围的!
- 我们接着取出堆顶也就是数组最小值把它放入数组下标为 0 的位置,注意我们小跟堆需要把那个堆顶 pop 掉!!!
- 我们再从数组的 k+1 下标的位置取出一个放入到小根堆,然后让那个 heap insert 或者什么什么的再次形成小跟堆
- 此时我们再取出堆顶也就是数组第二个最小的放入到数组下标为 1 的位置,注意我们小跟堆需要把那个堆顶 pop 掉!!!
- so on…
- 直到我们数组取不出元素了,到头了,我们就让现在的小根堆 pop 完后那个样子自己形成小根堆,然后取堆顶等等等就行了
- 最后我们数组都是有序了
我们小根堆每次只处理 k+1 个数,所以每次每一个元素 heapify 形成一个新的小根堆,其实就是 O (logk) 左右的时间复杂度
我们数组有 N 个元素,每个元素都要被放到小跟堆进行 heapify/heap insert, 也就是总共就共__O (NlogN) 的时间复杂度__
所以如果 k 的值很小,我们这个甚至就跟 O (N) 差不多了!所以堆排序很适合这个问题!!!
学到了 堆结构很管用!!!任何合适的都可以,任何想要我们选择某一个数,然后是按照某种跟其他的比较的规则,比如说比其他的都小 / 都大都可以!!!
注意我们可以用自己自定义的类的实例按照他们的属性的值来进行这个堆结构然后堆排序都可以,很自定义,很不错!
# 比较器和 java 底层的排序操作
就是一般:
- return 第一个参数 - 第二个参数,那么就是从小到大排 (貌似)
- return 第二个参数 - 第一个参数,那么就是从大到小排 (貌似)
- java 的 priority queue 直接用默认是小根堆,要是想要大根堆就要创建个类实现 comparator 接口重写 compare 方法并把那个类实例化传给 priority queue 的构造函数才可以实现实例化出来的 priority queue 是别样的,比如说大根堆,或者我们那个 priority queue 放我们自定义的类,也可以按照我们的某个属性 (我们定的规则) 来吧对应的放到堆顶
- 就是如果那个 compare 方法返回正数代表第一个参数 (或者那个类的某个属性的值等等等) 在顶堆,返回负数第一个参数放上面等等等
大根堆就是第二个减第一个参数就行了,如果是正数说明会把第二个放到堆顶,第二个数更大,所以放堆顶是大根堆
还可以自己自定义各种复杂的比较策略
java 底层的排序操作:
size 大于 60 时 使用 merge 和 quick 进行综合排序,如果小于 60,系统默认使用插入排序以求最快速度完成。
自己定义的 class 类型排序时,会使用 merge 排序, 为什么???原因当然是稳定性,自己定义的类型一般会想要稳定性的,快排又做不到稳定性。
这是因为小样本量的时候,N 平方没那么起的快,反之插入排序的常数系数啥的更低,所以小样本量的时候用这些 N 平方更快一些些,按照情况使用不同排序的优点
比如说
# 链表问题
# 找出两个有序链表共同值的节点
- 一个指针指向第一个链表头,另外一个指向第二个链表头
- 比大小,谁更小谁移动到下一个
- 如果遇到一样的,记录那个一样的,然后共同移动 (两个都往下一个移,说不定还有一样的)
- 任何一个链表到头了,结束
# 两个链表是否有回文结构
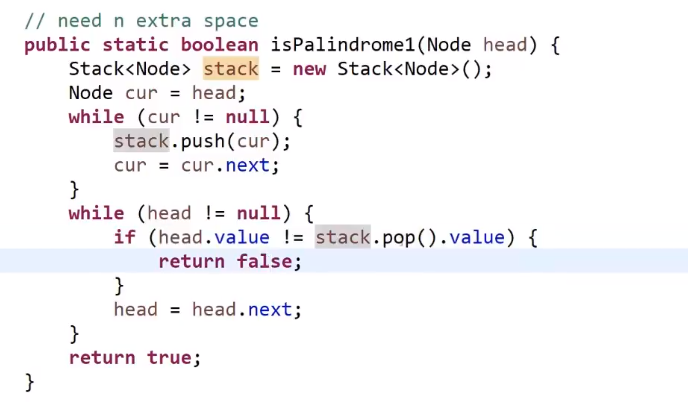
使用额外空间方式:
- 把每一个元素放入栈里面
- 从栈取出的顺序就是链表的逆序,我们边弹出边比较一不一样,如果回文结构一定一样,所以直到栈弹空要是还是都一样那么就回文
- 如果有一步不一样,就不是回文
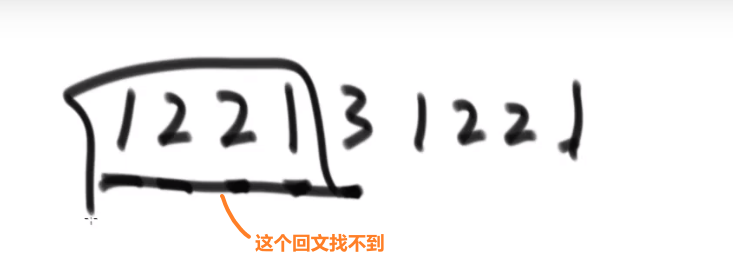
稍微再省一些空间的方法:
- 把链表右边的放在栈里面,然后再跟链表前一半比
- 栈只要弹空了就停
- 因为要是是回文结构,不管链表有的元素是不是偶数或者奇数个,反正比了左边和右边就会是一样的,就算是奇数个也不会 reach 到中间那个
但是我们怎么做到只把右边的放入栈?
快慢指针!
- 快指针比如说一次走两步
- 慢指针比如说一次走两步
- 这样最后快指针最后指向最后一个,慢指针差不多指到中间位置
这些快慢指针可以自己任何定制,按照自己想要的方式实现
我们想要
- 如果链表奇数个节点,我们慢指针指向中间那个
- 如果链表偶数个节点,我们慢指针指向中间的左边那个
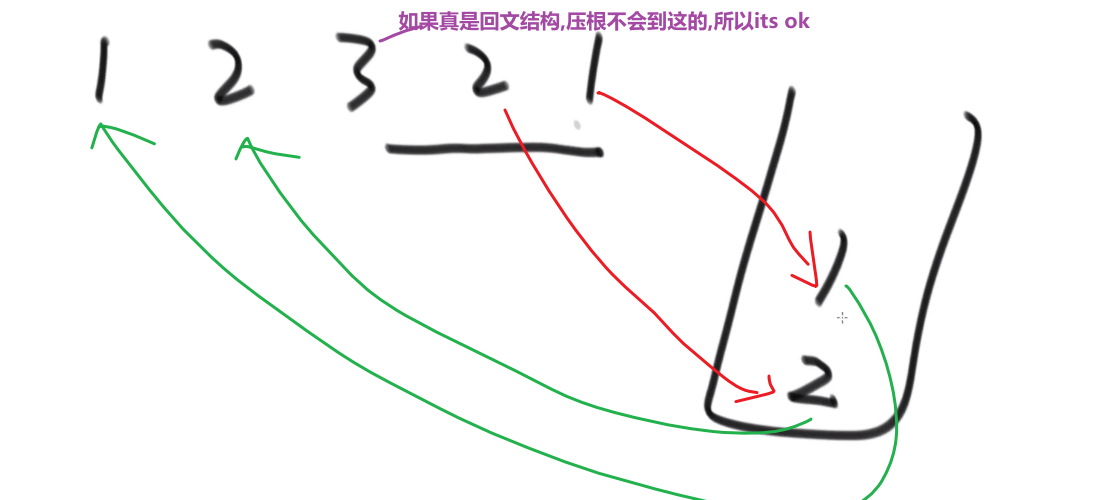
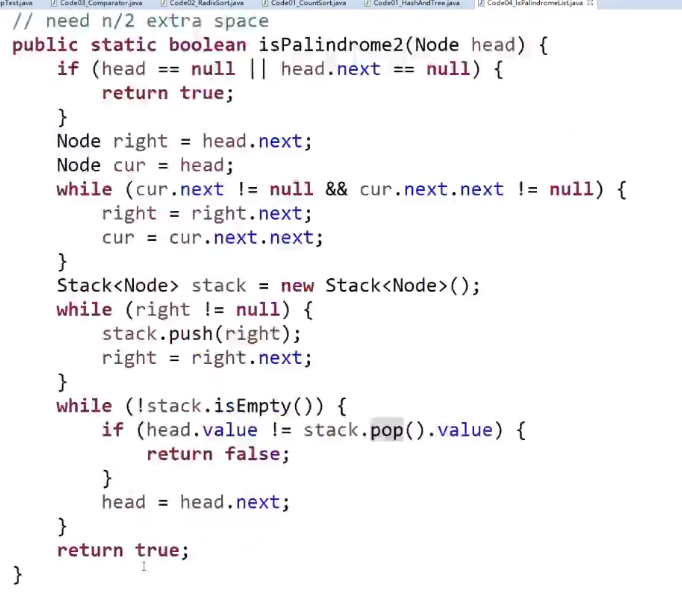
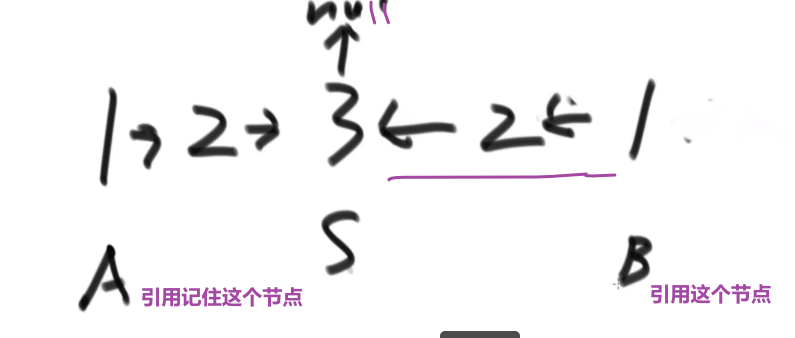
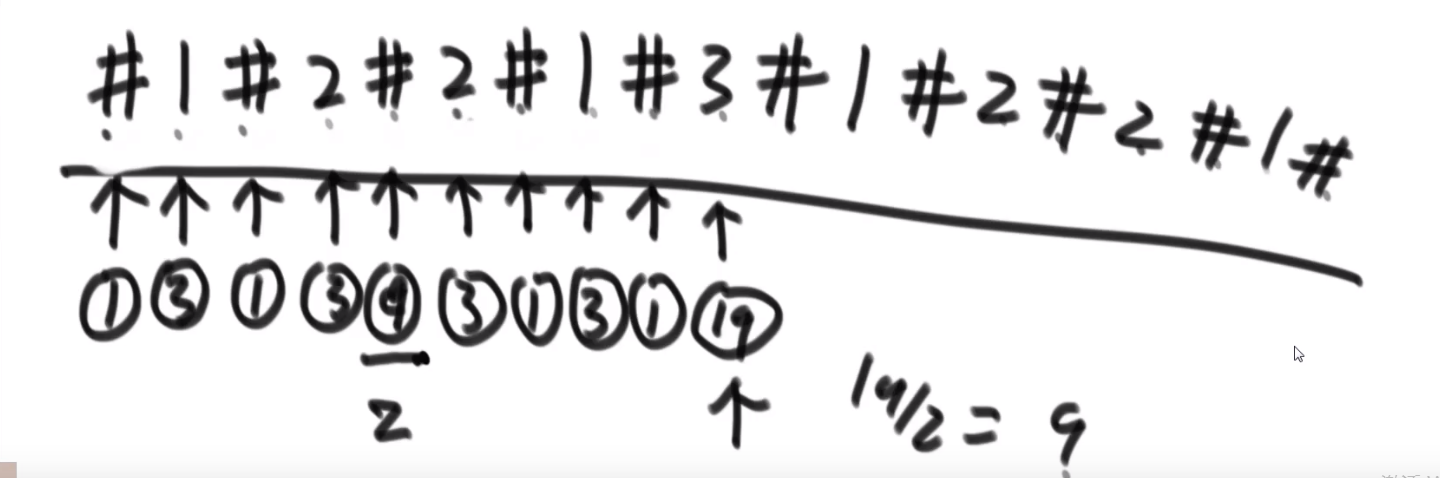
超级省空间的方法 (面试做的时候很加分):
- 快慢指针,最后让慢指针指向差不多中间位置
- 中间那个节点的 next 指向 null
- 然后让那个节点后面的节点都逆序
然后再 A 指针和 B 指针挨个比,一样的话就一块走下一个,如果有一个不一样就返回 false
一直到最后有任何一个为空 (null), 就停止,就说明最终结果就是回文结构
注意如果最后返回 true 的话,有时候需要把链表的指向恢复一下,看需求吧
这个对于偶数次的节点的链表也可以!自己想象一下!
这个方法就有限几个变量,最省空间的!!!
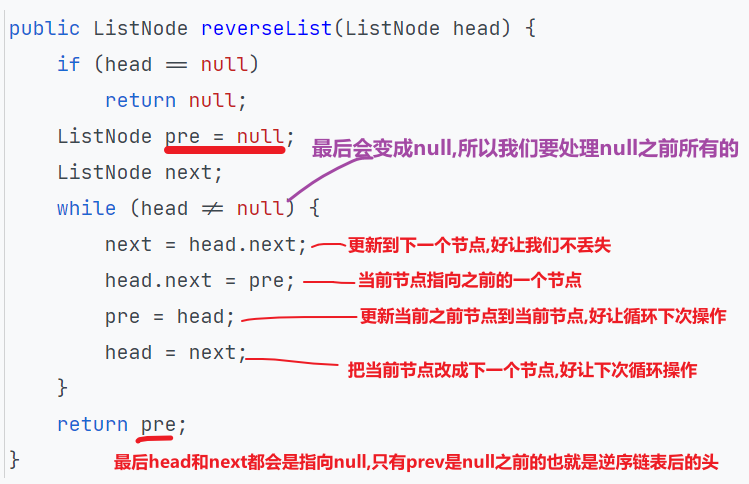
# 逆序链表
还有什么递归方式等等等
# 单链表按某值划分左边小,中间相等,右边大的形式
笔试里面做法:
把链表里面的数放到__Node 类型的__数组里面去,然后对数组玩 partition, 然后再把数组里面的数放回链表就行了
面试里面做法 (省空间!):
有很多类似于这种的问题,要多想想类似的看看这个解法适不适用
有些复杂我们用一个例子来讲解答案:
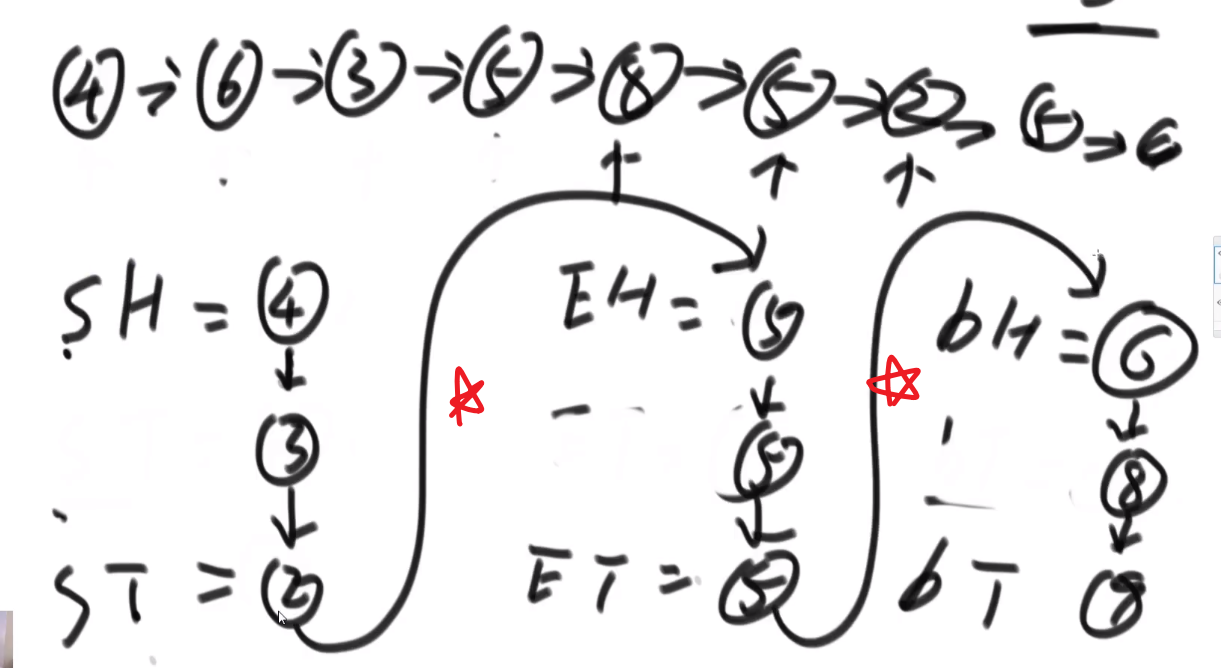
链表:
对于划分的值是⑤
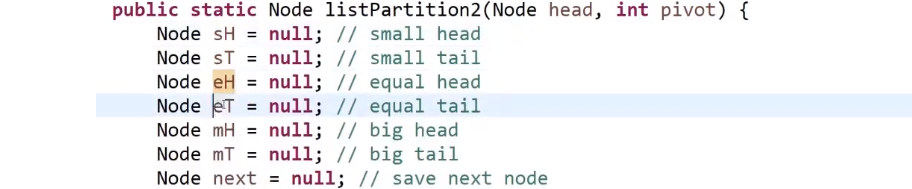
需要六个变量:
| 变量名 | 等于什么 |
|---|---|
| SH (一开始是 null) | 小于部分的头 |
| ST (一开始是 null) | 小于部分的尾 |
| EH (一开始是 null) | 等于部分的头 |
| ET (一开始是 null) | 等于部分的尾 |
| BH (一开始是 null) | 大于部分的头 |
| BT (一开始是 null) | 大于部分的尾 |
- 首先第一个节点④, 发现比我们的⑤小,所以让 SH 和 ST④
- 下一个节点⑥, 发现比我们的⑤大,所以让 BH 和 BT⑥
- 下一个节点③, 发现比我们的⑤小,所以让 ST 当前指向的节点④指向③, 然后让 ST 指向③(SH 不要动之后只有是一开始 null 的时候才会被第一个更新)
- 下一个节点⑤, 发现跟我们的⑤相等,所以让 EH 和 ET 都指向这个当前找到的⑤!!! 需要这个,因为可能有多个,我们要串起来所有相等的,然后让头代表第一个,尾代表最后一个 (可以看出是稳定的,保持了顺序,小于区域和大于区域都是同理)
- 等等等
- 最后就是:
- ST 的当前指向的节点的 next 指向 EH
- ET 的当前指向的节点的 next 指向 BH
== 不过注意!!!== 可能压根没有小于区域,可能压根没有等于区域,可能压根没有大于区域!!!
所以只有不是 null 的时候才可以调用 next 连,如果有一个是 null, 需要连下一个区域等等等
完成,结束!
我们相当于用很多指针 (基本上就是两个指针一个头一个尾代表一个区域,然后可能有多个这种对子), 然后我们就可以按照我们想来的规则把代表不同区域的指针头和尾指向不同节点 (期间需要如果那个区域的尾指针要换成别的,就让当前的尾指针 (如果不是 null) 的 next 指向新的那个,这样才能全部最终正确得串起来)
说到底就是那个链表,我们只是对节点的 next 改变就可以做很多事请
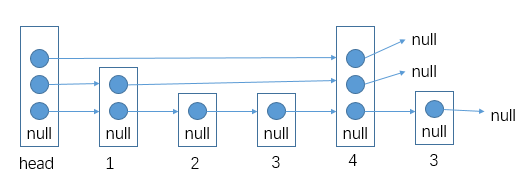
# 复制含有随机指针的链表
比如说:
使用比较多额外空间方式:
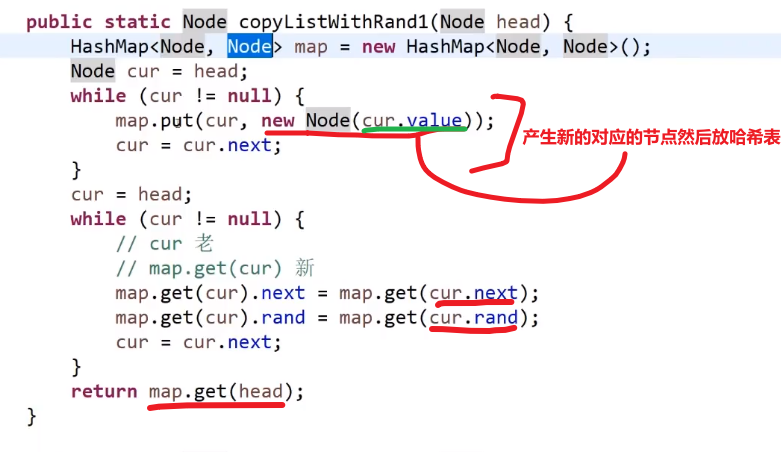
哈希表!HashMap!
- 遍历原来的链表,我们只需要把原来的链表的节点 (的指针) 和对应的新链表的新建的节点 (的指针) 作为 key 和 value 存入 hashMap
- 遍历老链表,或者遍历哈希表
- 对于每一个哈希表里面的值也就是新链表的节点的指针,我们让他的 next 指向这个新节点对应的 key (也就是老节点的指针) 的 next 指向的节点在哈希表里面对应的值,然后让他的 rand 指向这个新节点对应的 key (也就是老节点的指针) 的 rand 指向的节点在哈希表里面对应的值,就可以了
我们产生了一个 mapping (自己造的次) 相当于,就大概理念就这样!
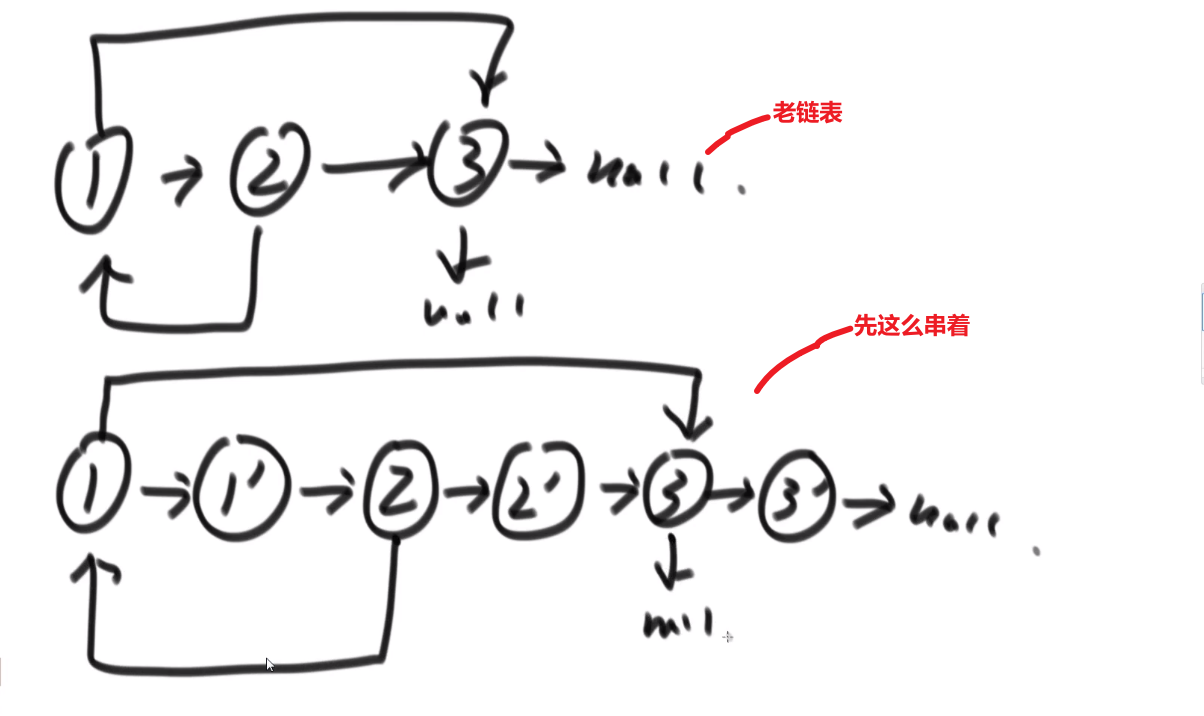
不使用比较多额外空间方式:
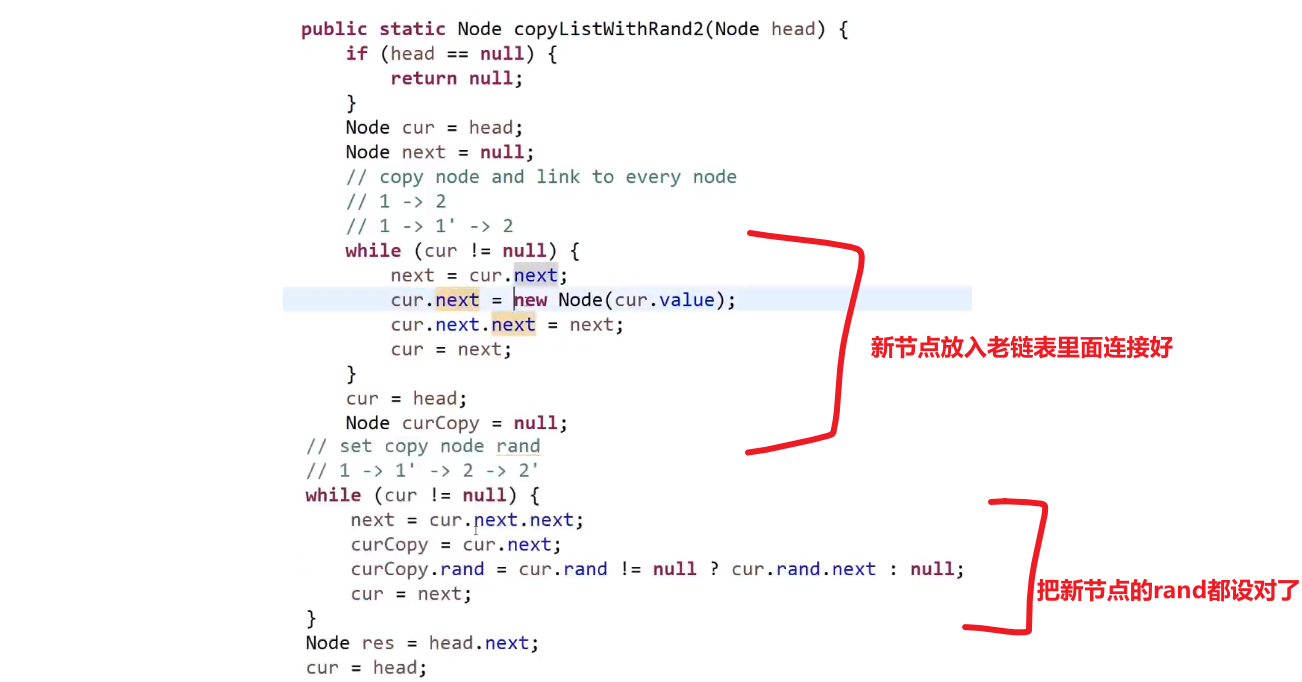
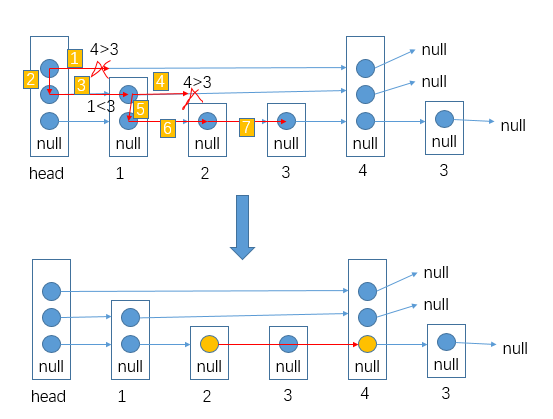
- 生成一个个新节点,但是我们让他们跟老链表的节点这么串起来
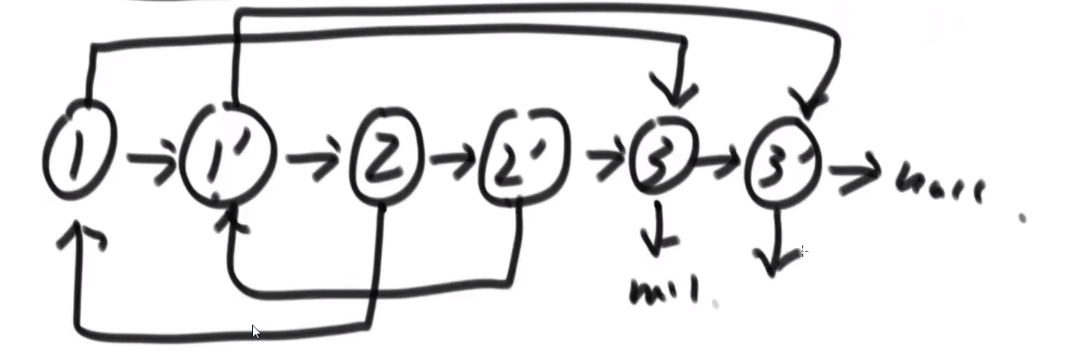
- 我们让每一个新生成的节点的 rand 指针指向当前这个新节点对应的老节点的 rand 指向的节点的 next
反正这种想法就是让老的节点和旧的产生连接,这样我们就可以按照老节点的方式连的连我们自己的这个新节点,毕竟我们想要的是复制嘛,肯定是照着来啊
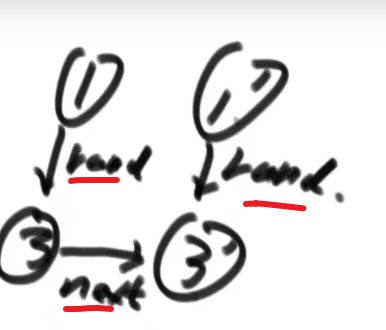
- 这么做后,就会成这样:
- 接着就把 next 改变,让新链表从这里分离出来
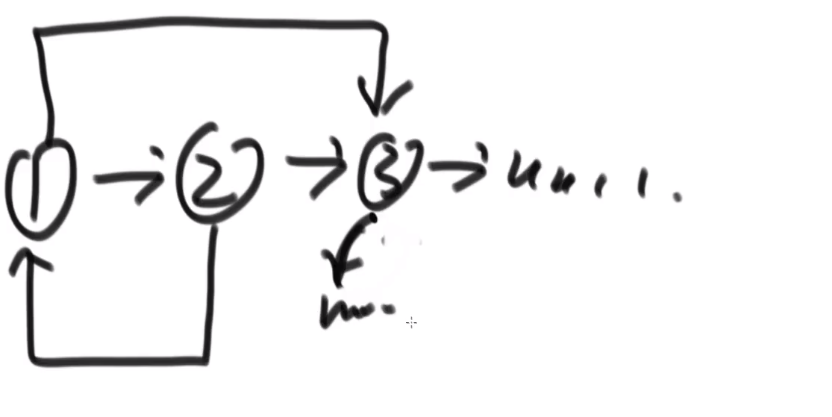
# 一个链表是否有环,如果有怎么找到入环点
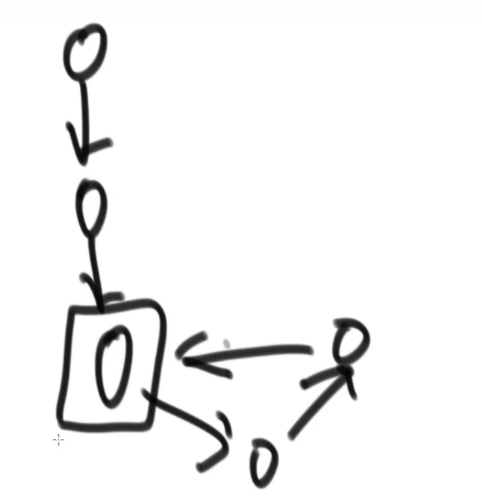
一个有环的链表,和他的入环节点:
可以发现有环的最终不会指向 null, 所以最后要是走到了 null, 说明肯定没有环
使用 HashSet 方式很容易:
- 每个节点 (存节点的 HashSet, 不是节点的值!!) 存入哈希表之前先看看是不是已经有了,如果没有才存,如果有说明有环
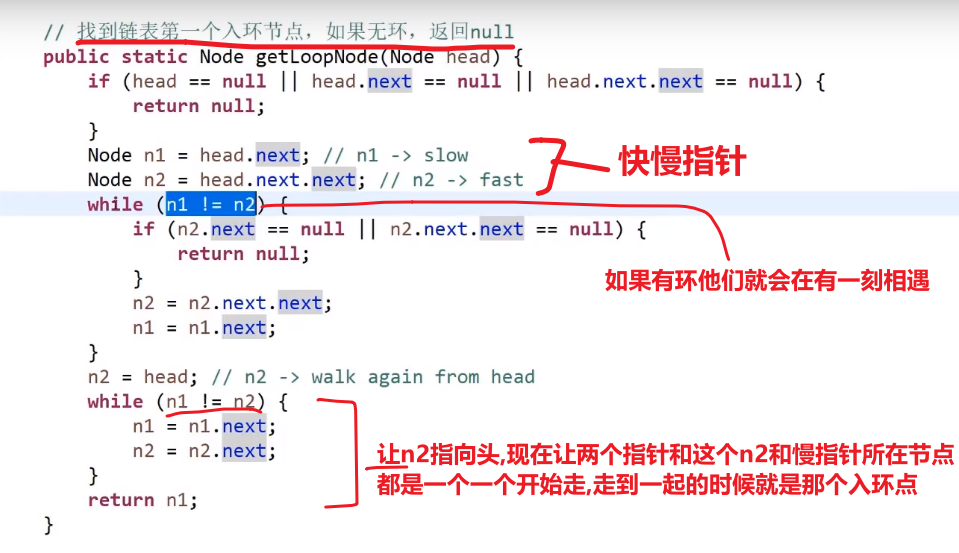
不适用那么多额外空间的方式:
* 快慢指针!!!*
链表好多都是快慢指针和哈希表解法啊
- 两个指针方法,快指针慢指针
- 如果一个链表有环 (说明最终不会指向 null)
- 那么快指针一下走两步,满指针一下走一步
- 他们肯定会在有环的部分相遇的! 并且满指针和快指针在环中转的圈数不会大于两次以上!!!
- 这个时候!接着让快指针指向 head, 然后跟慢指针一样一步一步走,直到他们相遇,他们相遇的那个节点一定是链表入环的节点!!!
# 两个单链表相交
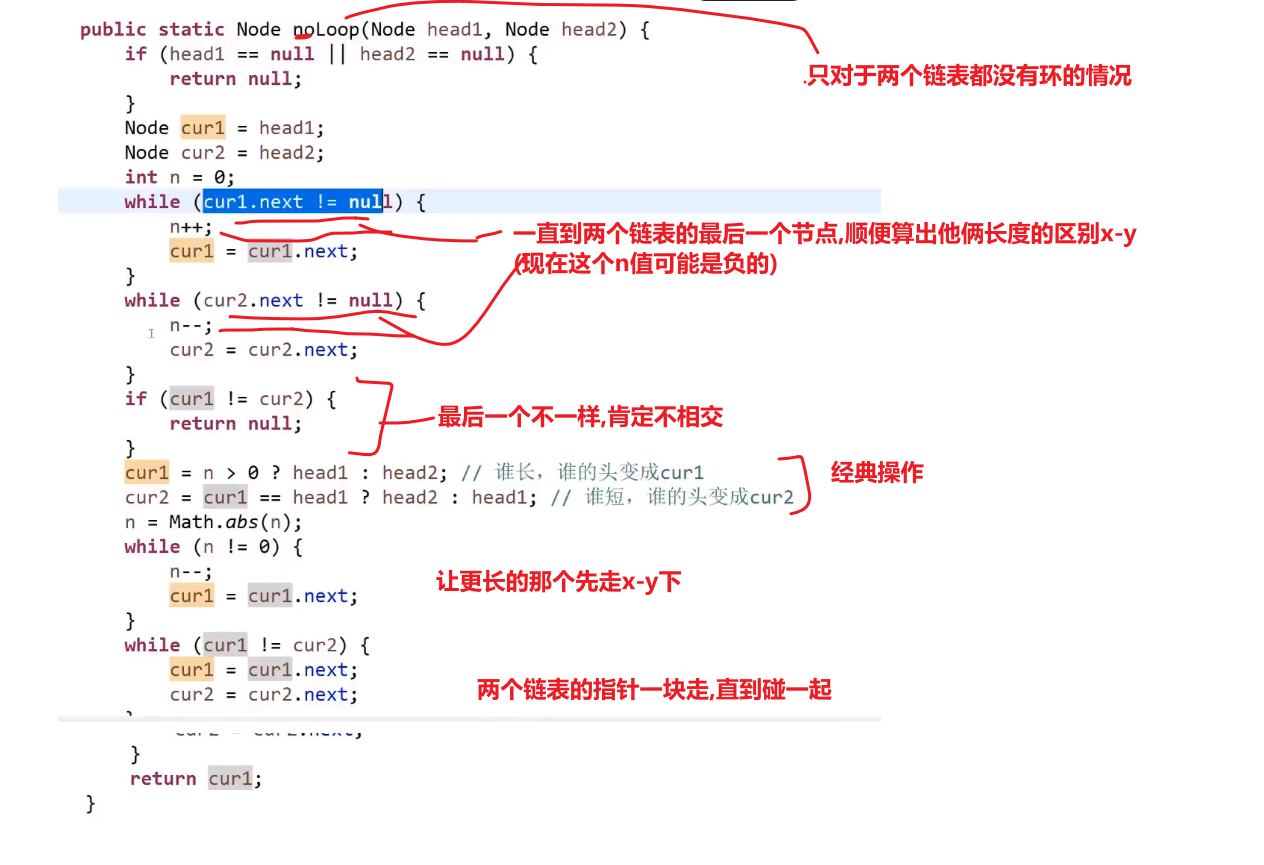
# 如果两条链表都无环
用 set 方式:
第一条链表节点都入 set,第二条链表查,查到重复即为相交节点
不用 set:
- 遍历第一条链表,记录最后一个节点,且记录链表长度 (长度记作 x)
- 遍历第二条链表,记录最后一个节点,且记录链表长度 (长度记作 y)
- 如果两个最后节点不同,则不相交 —> 如果相交最后一个节点肯定会是一样的
- 如果最后一个节点是一样的,那么 x 与 y 大的先开始走, 走 x-y 步 (如果相交,那么共享的部分肯定不会出现在那个 x-y 步里面,因为后面的长度都会是共享的部分,细品,细细品)
- 然后那个长的那个走完 x-y 步后,两条链表一起走,某一刻肯定会在相交的节点相遇
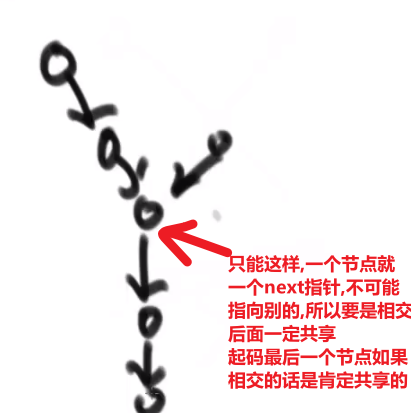
# 如果一条链表无环一条节点无环
这种情况绝对不会发生,因为只有 next 一个指针,只能最终指向一个方向
# 两个都有环
如果两个有环链表相交,那他们一定是共用这个环
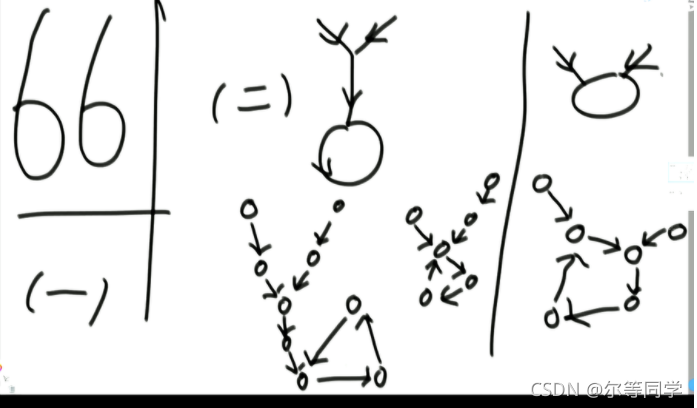
一共有三种情况
- 两个有环但是不相交
- 两个有环且相交点是同一个
- 两个有环且是靠着环来相交的 (这里我们认为任何一个链表的入环点就是相交点)
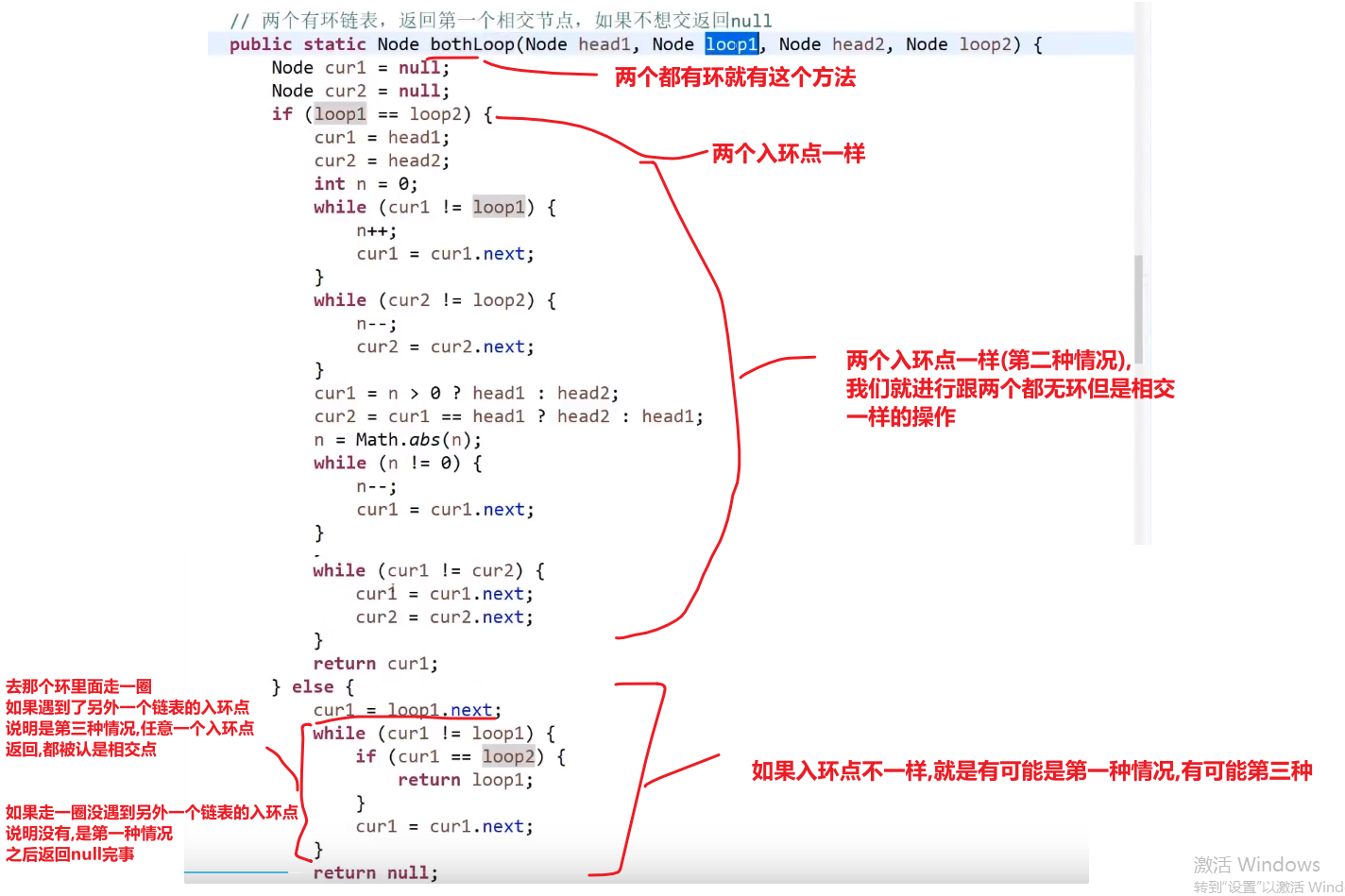
-
如果 loop1 (第一个链表的入环点) 的内存地址等于 loop2 (第二个链表的入环点) 的内存地址 -> 则为第二种情况 (两个入环节点一样)
- 那我们就用无环的方式就行了,差不太多的
-
如果 loop 1 不等于 loop 2
- 让 loop1 沿着环走,如果没有遇到 loop2 则为第一种情况,也就是没有相交
- 如果遇到了 loop2 就是第三种情况 (两个入环节点不一样)
- 无非就是有了两个头节点和两个链表的入环节点
- 如果入环节点一样,说明是第二种情况,就按照我们无环的做法一样就行,长的先走 x-y 步,然后两个一起一块走,一直走到一样的说明找到了相交点 (* 这个不一定他们的入环点,因为可能入环点之前就相交了,参考第二种情况的图片!!!*)
- 如果如环节点不一样,我们就 while loop 让那个 loop1 入环节点走一圈,如果这一圈没遇到和另外一个 loop2 入换节点,说明是情况 1, 如果遇到了一样的说明是情况 3-> 返回 loop1 或者 loop2 都行,都叫做第一个相交的节点
# 能不能不给单链表的头节点,只给想要删除的节点,就能做到在链表上把这个点删掉?
抖机灵
- 将删除节点的下一个结点的值赋值给删除节点
- 然后将删除节点的 next 指向下一个节点的下一个节点
- 然后删除下一个节点就行了
注意这个不能删除最后一个节点
# 二叉树问题
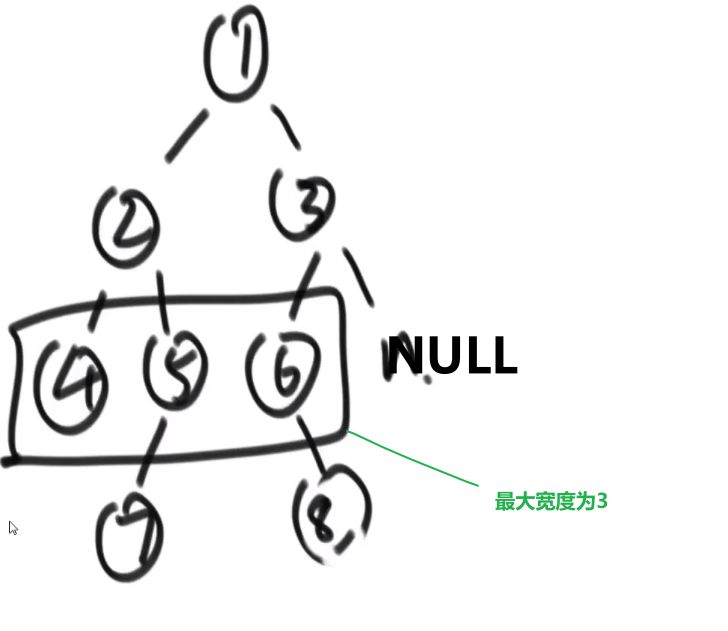
# 求一个二叉树的最大宽度
比如说:
我们只需要在宽度遍历的时候能知道当前的节点是第几层就能开始计数了
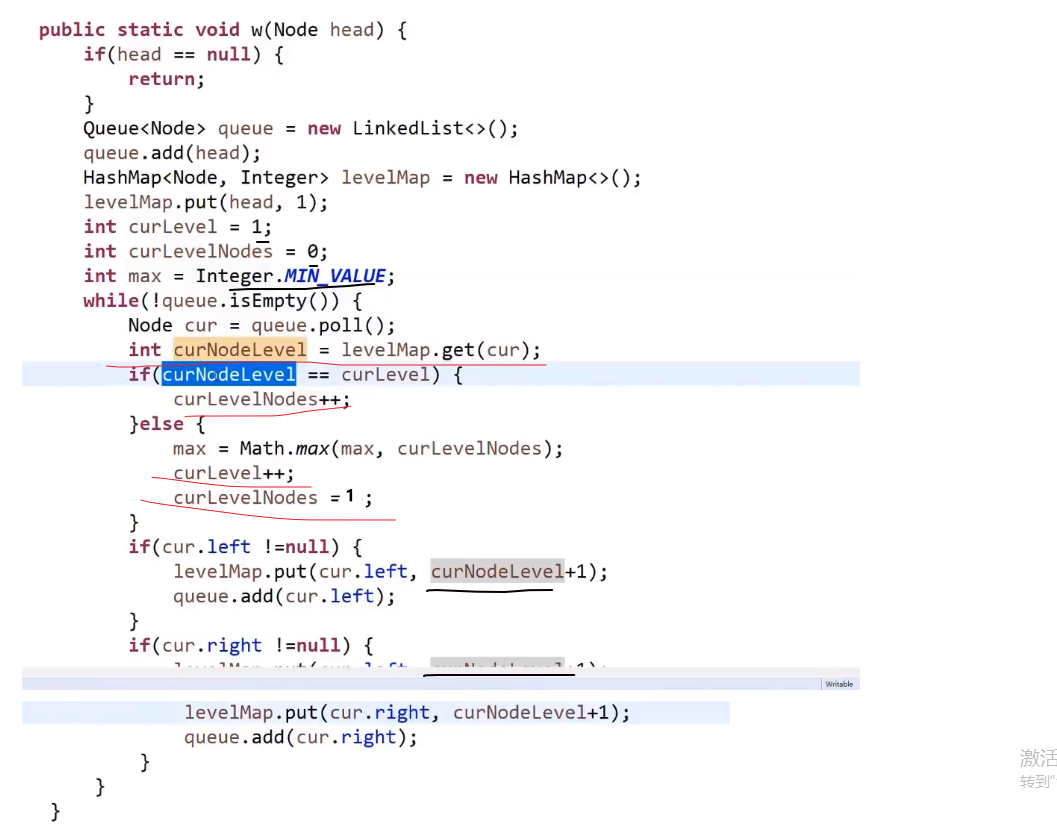
使用 hashMap!
下面的听个大概意思就行,不需要死记硬背
- 一开始我们把那个头节点插入到队列中,我们也 put 一个 key 为那个头节点然后 value 为 1 (代表第 1 层) 到 hashMap 里面去
- 到了我们循环里面,每次我们让一个节点出列,我们就靠这个节点来查 hashMap 里面对应的 value, 也就是那个出列的节点的值
- 如果取出的值跟我们当前操作的层次 (一开始设置为了 1) 一样,那么就说明当前是同一层的节点,我们就让保存那一层节点数量的变量 ++
- 如果取出的值跟我们当前操作的层次 (一开始设置为了 1) 不一样,那么就说明当前是下一层的节点,说明上一层我们那个那一层节点数量的变量已经是计算完了那一层的数量
- 我们就需要计算看这个跟我们当前用变量 max (一开始设置为了数字最小值) 比,如果更大,就要更新 max 值
- 并且我们还需要把那个当前层数的变量 ++
- 然后清空当前层一共多少节点的那个变量设置为 1 (因为当前就是这一层的节点,所以发现了一个)
- 然后就是之前的宽度遍历部分先让非空左节点的进队列
- 我们把这个非空左节点作为 key 存入 hashmap, 他的 value 就是当前保存层数的变量 + 1
- 再让非空右节点的进队列
- 我们把这个非空右节点作为 key 存入 hashmap, 他的 value 就是当前保存层数的变量 + 1
上面代码有点 bug, 比如说出列最后一个节点时,可能会没有到 Math.max (那里比较), 也就是没有比较最后一层
# 如何判断一颗二叉树是否是搜索二叉树
搜索二叉树就是每一颗子树,他的左孩子都要比头小,他的右孩子都要比头大
经典的搜索二叉树没有重复的
答案:
我们直接使用中序递归–> 左中右,如果是搜索二叉树,那么最后中序递归出来的顺序一定是升序的
如果某个点不是升序的,那就不是搜索二叉树
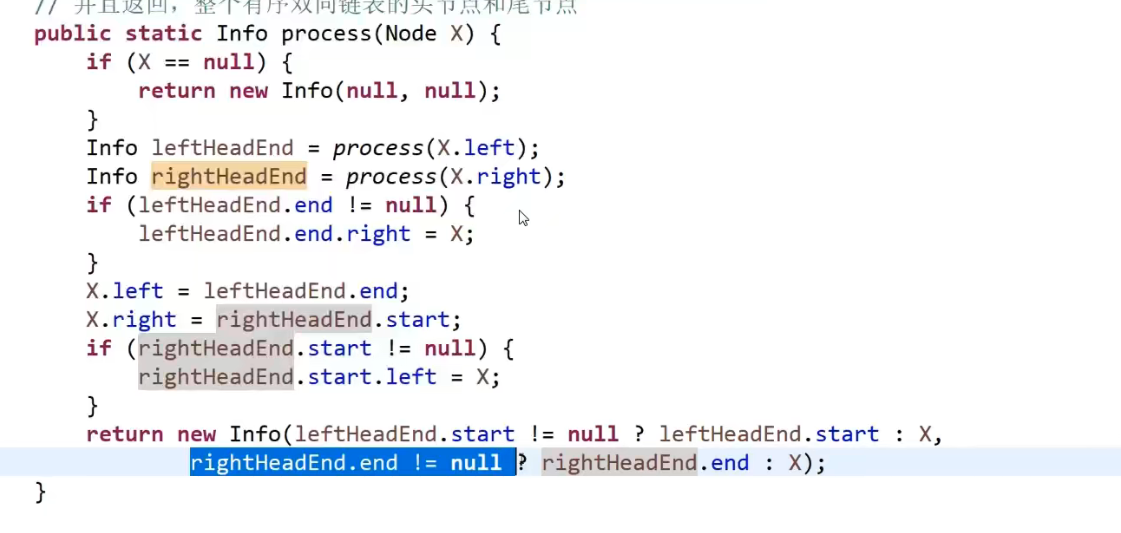
递归方法:
递归的想法就是把问题缩小到你最关心的大小上,比如说这里最主要的是每一个节点 (mergesort 最小的就是两个连着的元素,等等等), 然后这里这个可能不是最小的,比如说 leaf 也是一个节点,但他的左孩子和右孩子是 null, 我们一般不会用到 null 做什么处理,就测如果 head==null 那就怎么怎么样直接返回等或者返回 true/false. 这样就足够了,因为回调自己的 null 左 / 右子节点都会遇到这个。接着就是在合适的顺序,处理那个那个你关心的最小单位,爱这里处理你只要关心你那关心的节点就好了 (可能一个,可能两个,等等等), 当然他们的结果可能是当前回调自己参数传进来的,可能是来自之前回调自己的结果等等等,反正你可能会有多个自己的调用,顺序很重要,返回值也重要!
我们把关心的那个范围的节点处理好了,我们只要保证其他节点 (或其他) 都要经过我们设置的操作就行,如果是返回什么值,一定要注意所有可能性,有没有需要多些 if 看看情况等等
就是我们左边子树需要先判断,也就是一直到左节点,这里我们再跟我们那个比较逻辑比,然后返回上一层,上一层会调用右边的逻辑也是那一层的 head 比 (还没必过!) 然后让右子树也这么做,要是都对了返回 true 到他的上一层,到了这一层又要拿那一层的 head 跟那个比,然后右子树也这么做 (因为还没处理过).
但是我们如果这整个有哪个返回 false, 我们直接作为上一层的左子树调用,返回了 false, 然后我们那个一层还没判断这个左边的是不是 false 就直接拿他的一层的 head 比较,万一比过了,那就是 true 了,明明他的左子树没有符合,但他这一层却把整个他所代表的他自己 (head) 和他子树的结果返回为 true 了,这肯定不对!!!我们要先测左边的对不对,要是不对,直接让这个一整层就返回 false,head 也不用比了,右子树也不用比了,直接一直返回到一开始的 (栈底) 的那个一层然后直接返回 false 作为整个方法的结果.
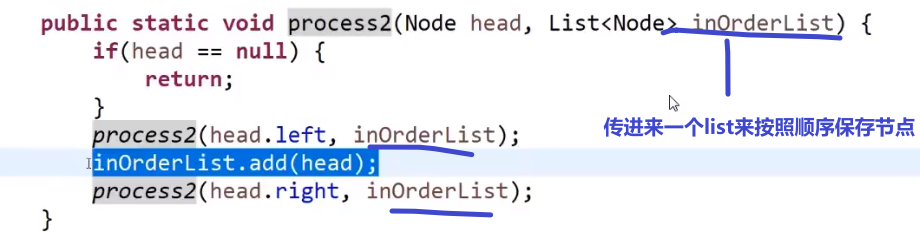
比较费空间的写法:
然后再主函数调用这个方法传参数,接着我们只要对那个传进去的 list 在这个方法结束后遍历一下,看看是不是升序的就行了
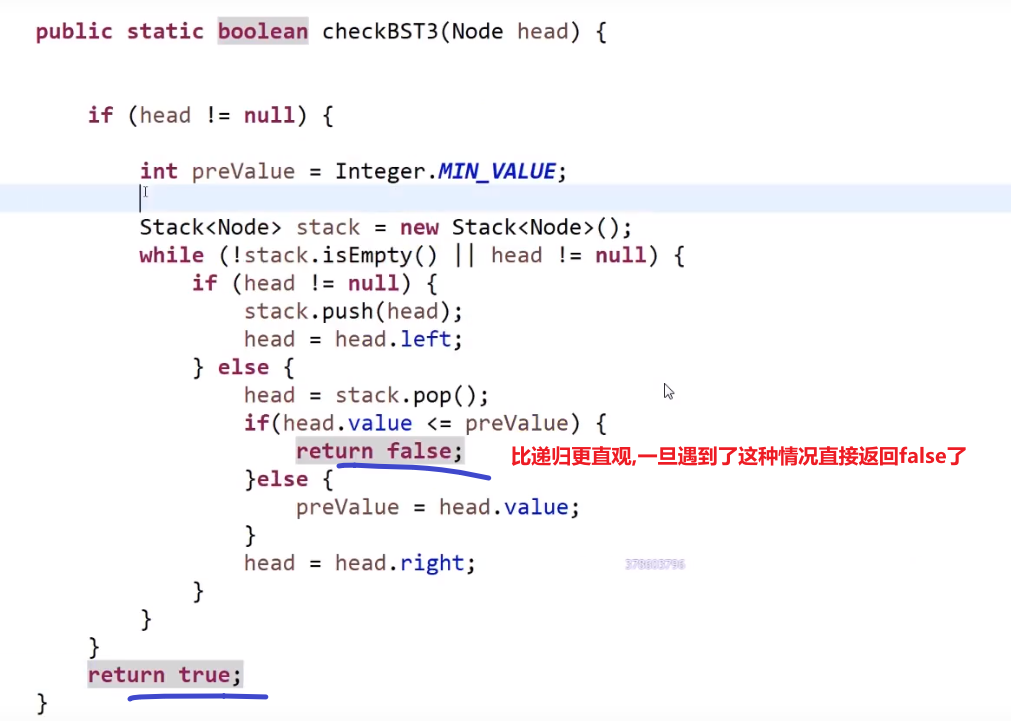
非递归方法:
同理:我们当然可以做到–> 后头左,这个样子的中序,看你什么需求了
# 如何判断一颗二叉树是否是完全二叉树
完全二叉树就是要么全满,要么左边往右填,右边的还没满
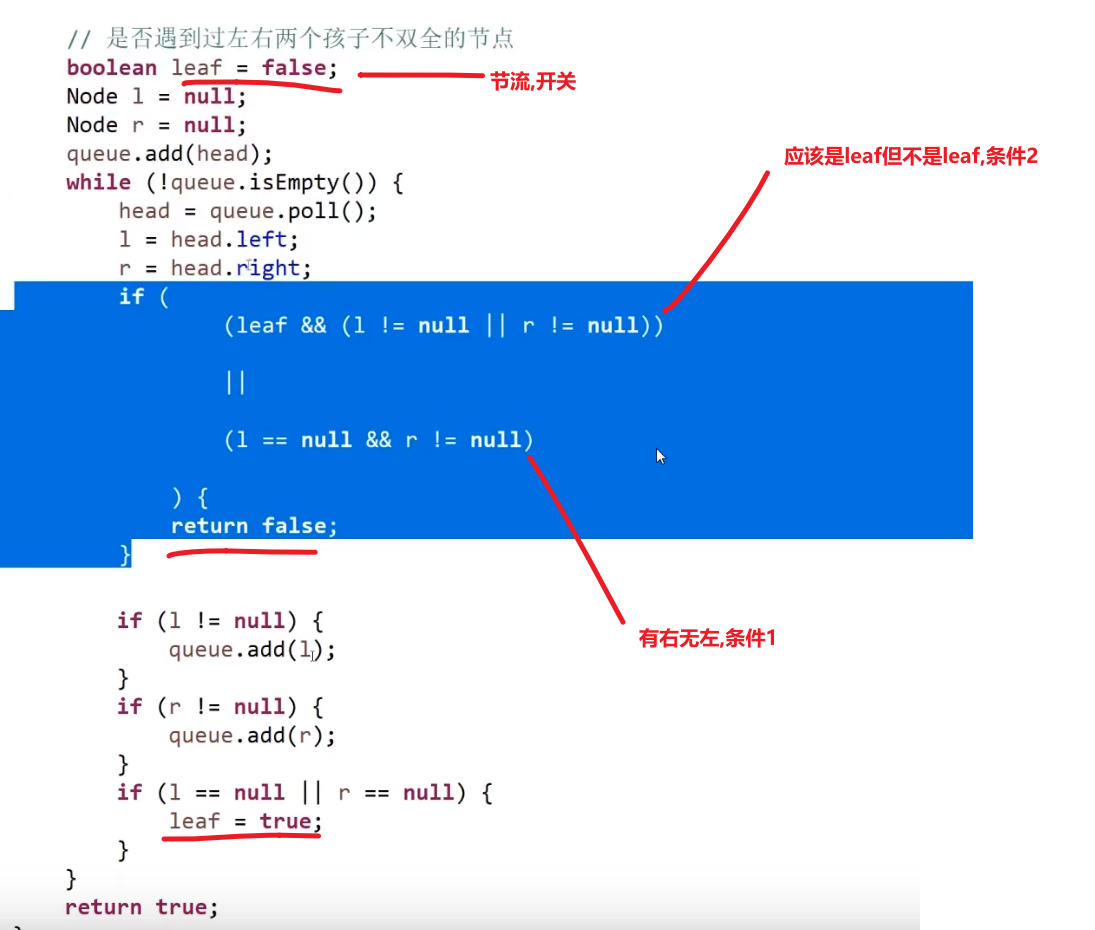
答案: 使用宽度遍历!
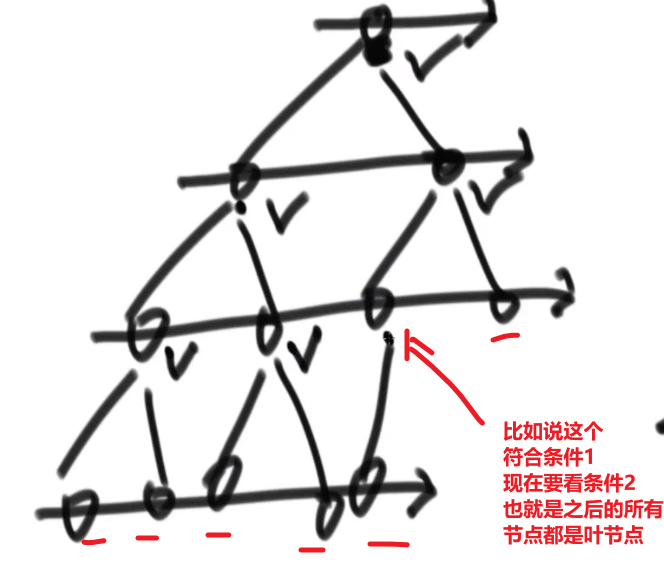
- 遇到的每一个节点,如果这个节点有右孩子没有左孩子,直接返回 false
- 在第一个条件不违规的情况下,如果遇到的第一个节点他要么只有左孩子,或者两个都没有 (复合第一个条件), 那么之后的所有节点都必须是叶节点,如果不是则返回 false, 如果都是返回 true
# 如何判断一颗二叉树是否是满二叉树
麻烦但好理解的做法:
- 有个函数统计这个树的最大深度 (D)
- 有个函数统计这个树的节点个数 (N)
满二叉树一定符合 N = 2D-1
# 如何判断一颗二叉树是否是平衡二叉树 (以及树型 dp 套路介绍⭐️重要!!!)
这里就可以说到了二叉树题目 (判断是不是满二叉树,是不是搜索二叉树等等等) 的套路!注意这里的逻辑,很重要!以后遇到问题这么来没差
平衡二叉树就是对于任何一个子树来说,他的左子树的层数和他的右子树的层数相差最多为 1
对于一个头节点来说
- 他的左子树是平衡的
- 他的右子树是平衡的
- 然后 | 左高 - 右高 | <= 1
才可以代表这棵树是平衡二叉树
所以我们需要
- 左边是不是平的?以及高度是多少?
- 右边是不是平的?以及高度是多少?
所以我知道,左树和右树需求是一样的,那就递归
# 同理看是不是搜索二叉树还是使用同一个套路 (递归)
就像给了我们一个节点,问我们这个节点以及他下面的这个树是不是搜索二叉树
- 首先左边是个二叉树
- 右边是个二叉树
- 并且左树的最大值应该小于我 (这是对于每一个子树 (有左孩子的) 来说,因为是递归,确实啊,没毛病)
- 并且右树的最小值应该大于我 (这是对于每一个子树 (有右孩子的) 来说,因为是递归,确实啊,没毛病)
== 我们可以跟他的_左树要信息,可以跟他的_右树要信息,我们再看有什么需求 (要什么信息)==__
我们需要左树的信息
- 是不是搜索二叉树
- 这个左树的最大值
我们需要右树的信息
- 是不是搜索二叉树
- 这个右树的最小值
但是!我们递归全都是一样的,参数等等等
所以, 不管是哪边的树,我们都会让他返回三个信息
- 是不是二叉树
- 最小值
- 最大值
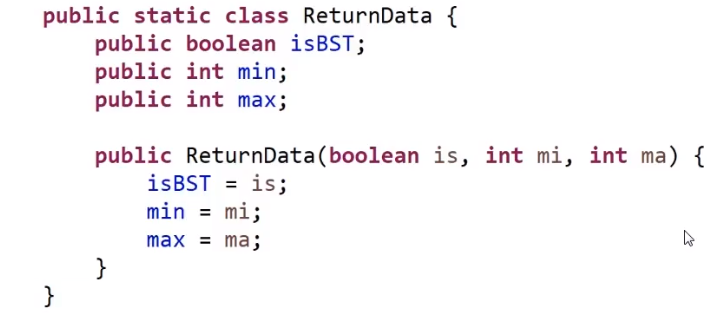
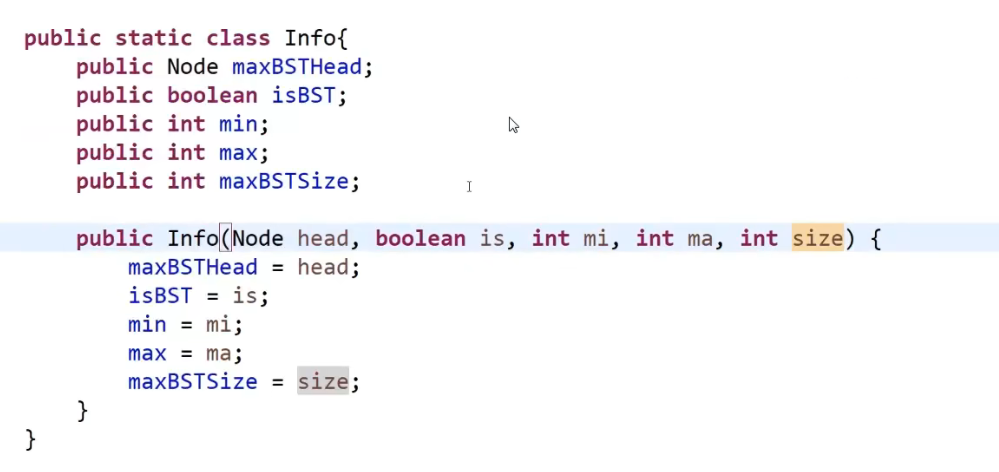
代码:
首先是自定义返回值:
# 同理看是不是满二叉树还是使用同一个套路
比如说给我们了一个头节点,我们要看是不是满二叉树,我们
- 首先知道他左子树的高度以及多少个节点
- 再知道他右子树的高度以及多少个节点
我们可以结合当前节点的信息 (高度加 1, 节点加 1), 然后调用这个这个 formula—>N = 2D-1
满二叉树一定符合 N = 2D-1
我们需要左子树的信息:
- 多少个节点
- 最高什么高度
我们需要右子树的信息:
- 多少个节点
- 最高什么高度
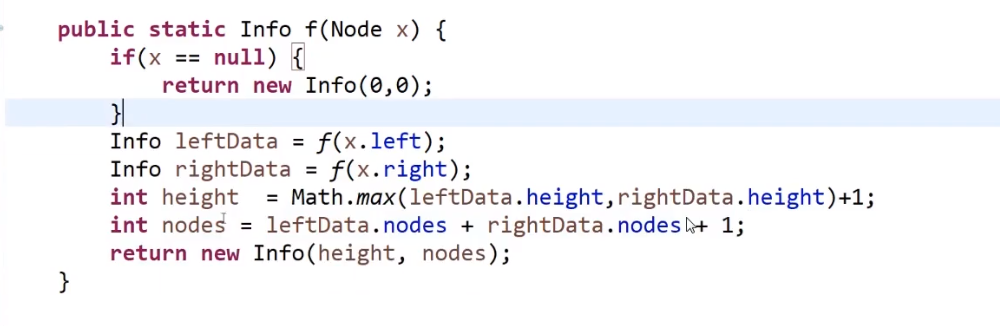
所以我们自定义返回值就是有这个两个属性
模板
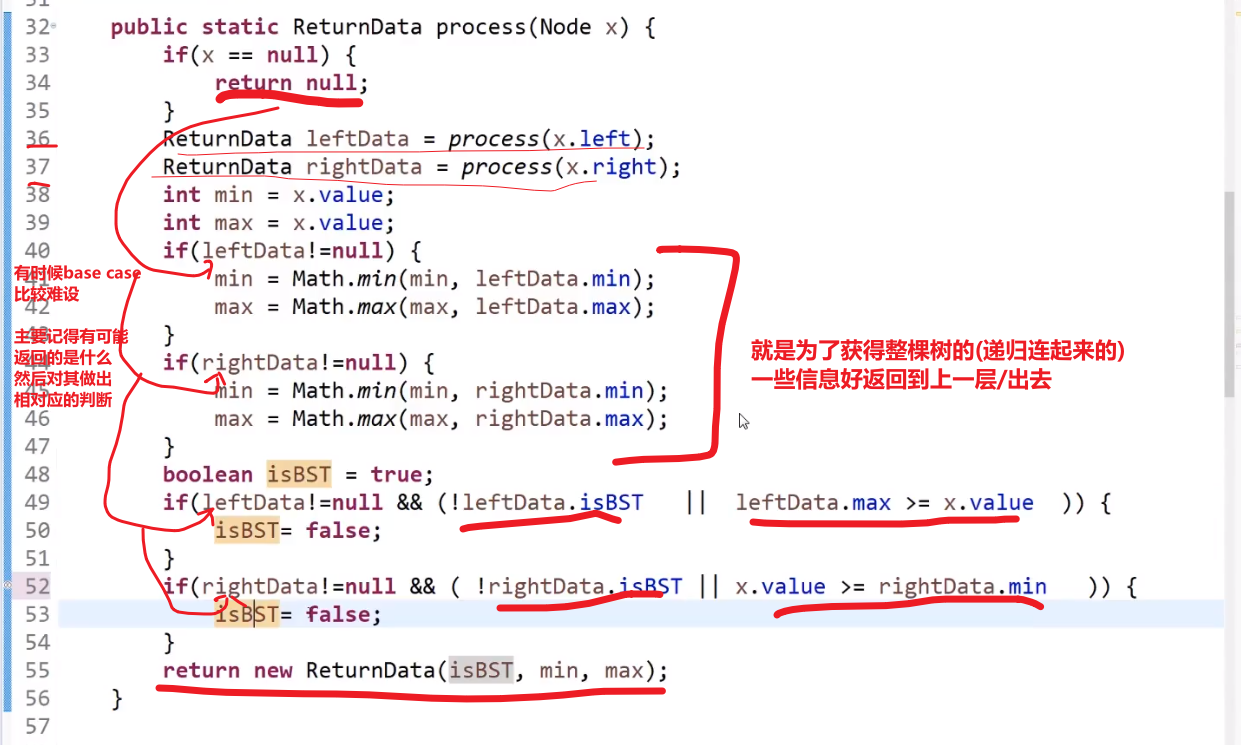
正确答案:
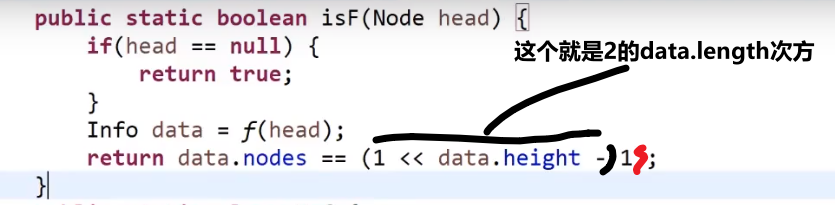
主函数调用:
这里相当于是先把所有要的值都获取了,然后才一块判定对不对
而不是之前那种让每一个左树 / 右树附带一个 isFull 这种数据作为返回值等等等
# 树型 dp 套路
这个不一定可以解决所有二叉树问题,但是可以解决所有树型 dp 类型的题
比如说,需要看整棵树才可以决定的答案,这种需要结合所有情况来看的,不过这种一般都是没有优化的方法,都是暴力解,面试中一般不会考的
树型 dp 的题就是解一个题可以通过跟左树和右树要信息,把这个事给解决了,只要是这种类型的,都可以这个套路解决
所以发现套路了吧!!!
我们一般都是自定义返回值,里面存着我们想要的 (不管是左树还是右树还是什么) 各种信息
然后递归方法里面,首先返回值肯定是我们的那个自定义的返回值,然后一般接收参数也是一个节点 (当前的头节点)
我们 base case, 这里一般要看你感兴趣的范围以及返回的值都是看你需求
接着调用自己传参传当前节点左边的树,然后这个返回一个我们自定义类型的值代表我们每一颗子树都有可能返回的值 (不用管那么多其实,就当做是黑盒,你只管调用自己就行)
反正最后会返回给你那个想要的左边树的信息
接着调用自己传参传当前右节边的树,然后这个返回一个我们自定义类型的值代表我们每一颗子树都有可能返回的值 (不用管那么多其实,就当做是黑盒,你只管调用自己就行)
反正最后会返回给你那个想要的右边树的信息
_我们接下来必须要考虑有了左边数的信息和右边树的信息,他们怎么和我们当前这个节点比,才能让他们连起来 (这个很重要!!!)_
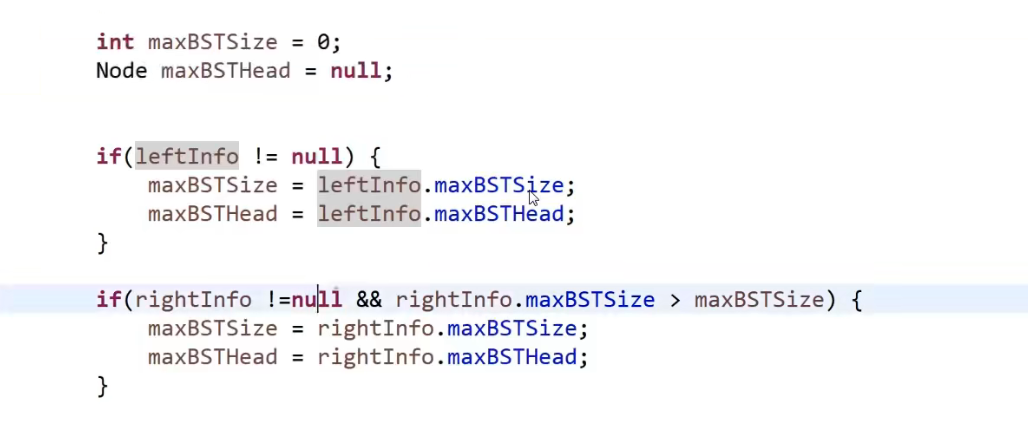
- 我们首先可以给那个自定义类的每个属性定义一个变量代表
- 接着对着每一个变量,让他们,结合着左边数的信息和右边树的信息来设对应的值
- 然后我们再把这些值封装成我们自定义类然后返回,作为我们这个当前整个树的返回值 (这个因为会是递归,会被每一个能算是被叫成树的 (有左孩子 / 右孩子 / 都有等等等) 都会执行这一块)
再多说几句:
我们在最后处理当前节点的,只要考虑我们左边数的信息和右边树的信息就行了,比如说左边数的信息和右边树的信息里面有最小值,直接用,那肯定就是我们左树 / 右树一个一个算出来最后到了那一层算出的最小值 (就认为左 / 右树给的信息就是全量的–> 我们想要的信息都有,“比如 36,37 行的递归代码,我管你怎么执行,反正你把我要的结果给我了”), 然后我们这一层再比,跟当前节点比,如果当前节点更小,那么更新那个最小值,由此可见,其实最小值就是这么更出来的,最后这个也会返回到上一层!
这个套路可以解决一切面试里面的树型的 dp 题
# 树型 dp 题之二叉树节点间最大距离问题
两种可能性
- 不包括头节点 x, 说明就是要么 x 的左树 / 右树有两个节点他们之间距离最大
- 包括头节点 x, 说明就是 x 左树最深的节点到 x 右树最深的节点 (也就是
左高+右高+1(x他自己))
所以就是左边取最大距离,右边取最大距离,然后左高 + 右高 + 1 (x 他自己), 这三个当中取最大值
这种按照头节点包不包括的可能性分类就是经验,这种可能性的分类很重要!
树型 dp 套路
- 左树和右树都需要最大距离 (这个最大距离就是按照每一层的节点以他来看高度的得出来的) 和高度信息
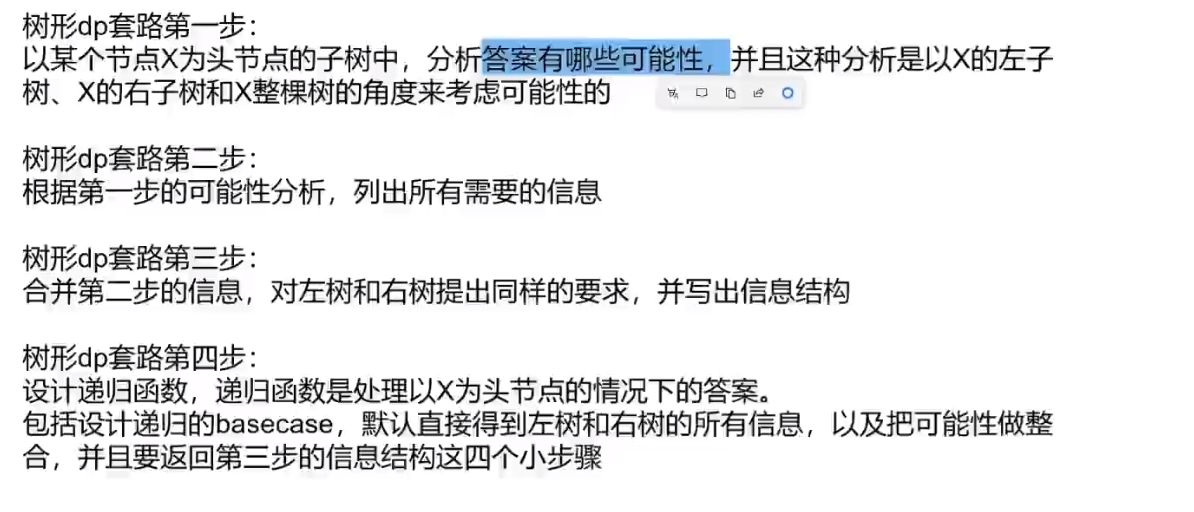
# 树型 dp 题之排队最大快乐值问题
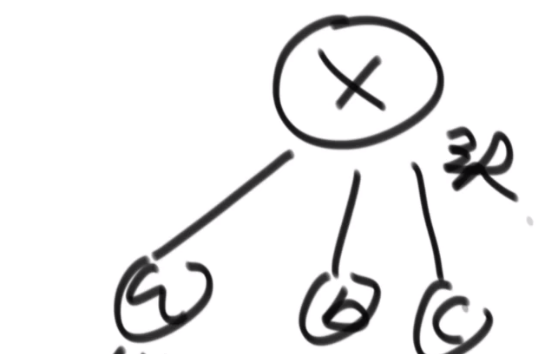
这个是个多叉树的结构
解法:
假设 x 头节点,然后直接孩子是 a,b,c
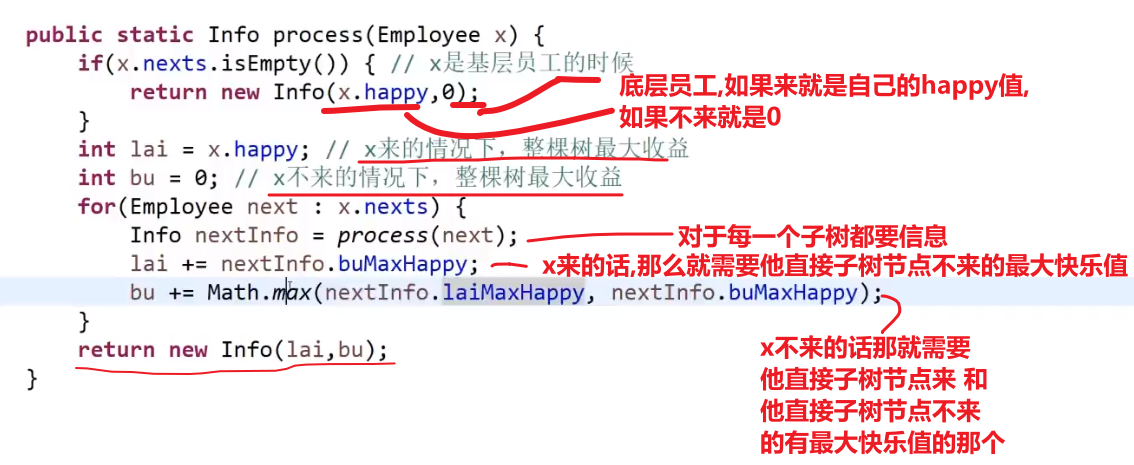
- x 参与,代表 abc 就无法参加,那么整颗 x 代表的树的最大快乐值就是
x快乐值+a整棵树在a不来的情况下最大的快乐值+b整棵树在b不来的情况下最大的快乐值+c整棵树在c不来的情况下最大的快乐值
- x 不参与,代表 abc 可以参加也可以不参加,那么整颗 x 代表的树的最大快乐值就是
0 + Math.max(a整棵树在a来的情况下最大的快乐值,a整棵树在a不来的情况下最大的快乐值) + Math.max(b整棵树在b来的情况下最大的快乐值,b整棵树在b不来的情况下最大的快乐值) + Math.max(c整棵树在c来的情况下最大的快乐值,c整棵树在c不来的情况下最大的快乐值)
所以对于我们的所有子树 (多叉树), 我们需要:
- 那个子树包括子树节点来的最大值
- 那个子树不包括子树节点来的最大值
树型 dp 套路可以对多叉树也可以用,都是那个想法
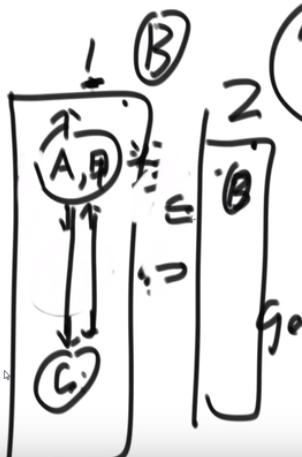
# 两个二叉树的最低公共祖先
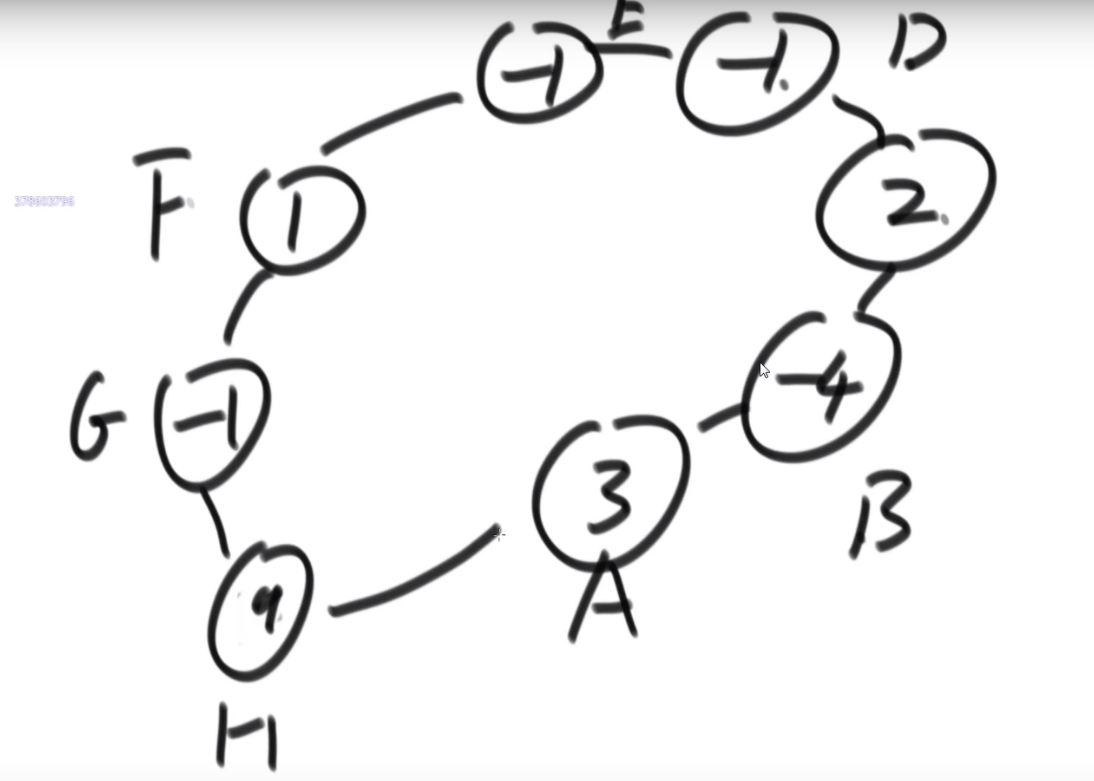
比如说:
- D 和 E 的最低公共祖先是 B
- E 和 F 的最低公共祖先是 E
所以问题就是整个二叉树的头给我们,然后给了那个 node1 和 node2
潜规则,node1 和 node2 一定是属于 head 为头的这个二叉树的节点
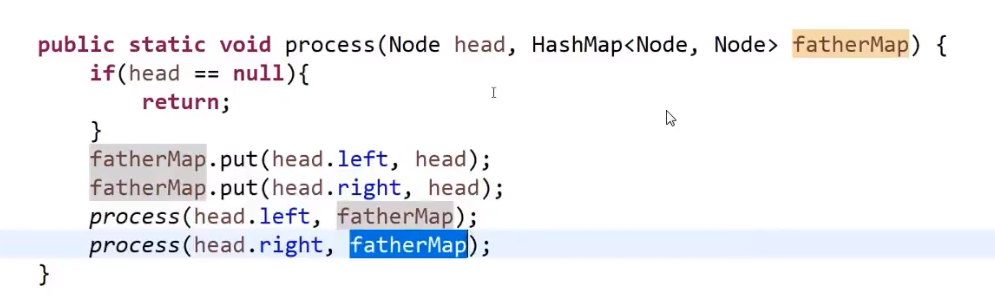
- 使用 HashMap 来存每一个节点 (key) 和他的父亲 (value)
- 接着把 head 和这个 hashMap 作为参数传进一个递归方法
- 这个递归方法里面的套路就是模板 (有稍微一点不一样)(只不过我们这里没有返回值,不用自定义返回值类型,我们只是改 hashMap 里面的数据)
我们在这个递归方法里面:
- base case
- 把左节点作为 key 和当前 head 作为 value 存进 hashmap
- 把右节点作为 key 和当前 head 作为 value 存进 hashmap
- 调用自己左子树传进去 hashMap
- 调用自己右子树传进去 hashMap
这个样子所有左子树会把他的所有节点和对应的父亲都设置好放进了 hashMap, 所有右子树会把他的所有节点和对应的父亲都设置好放进了 hashMap, 我们就可以返回到我们的主函数里面再做操作
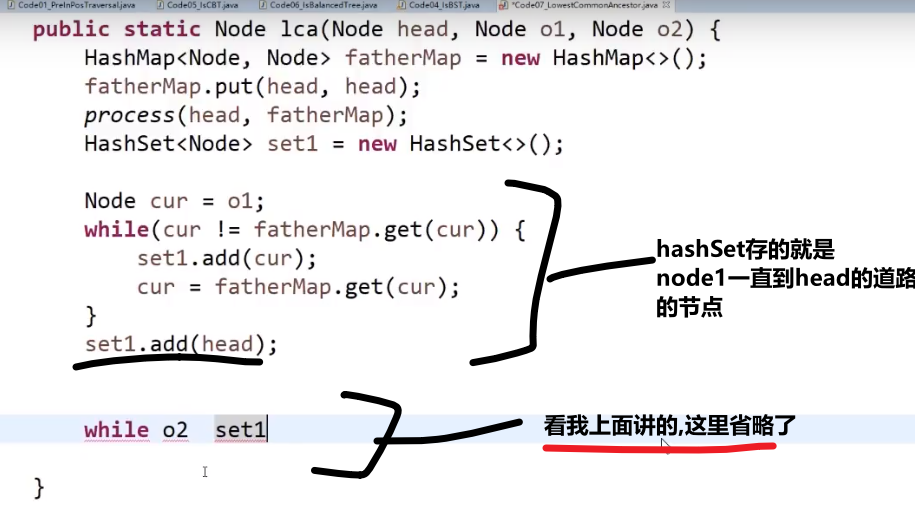
- 首先,我们 ** 整个的大头 head (只有这一个!)** 他的父节点是没有设置的,所以在主函数一个设置一下
- 然后使用一个 hashSet 把 node1 (或者 node2) 先放进去
- 然后接着一直放,放到头节点 (包括) 为止,此时这个 hashSet 就是这个 node1 到头节点的道路经过的节点
- 然后接着我们可以使用 hashMap, 让 node2 检查是不是已经在那个 hashSet 里面了,如果没有一个一个往上升 (变成他自己的父亲), 然后一个一个检查,直到查到一样的 (可能是 head 主的那个头节点), 然后返回那个节点就行了,因为就是从下往上的 (通过成为找父亲,找父亲的父亲), 要是有一样的 (一定会有的,因为最后肯定都是 head), 那么一定就是最低的公共祖先
# 更短,但是很难理解的方法
https://www.bilibili.com/video/BV13g41157hK?p=7&spm_id_from=pageDriver
1:35:00, 比较抽象
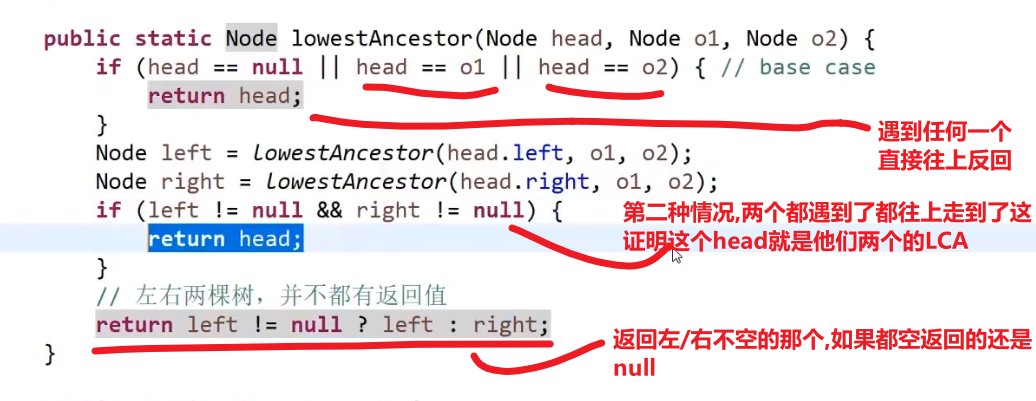
有两种可能
-
O1 是 O2 的 LCA (最低公共祖先), 或者 O2 是 O1 的 LCA
那么我们直接把那个更上面的那个返回出来,另外一个没有遇到 (根本不去), 代表最后只有一个然后另外一个是 null
那么整体返回的就是那一个,也就是对的
-
O1 和 O2 不互为 LCA, 要往上才能找到
那么这两个都会被找到然后往上传,一直传到他们的 LCA 就会直接返回那个 LCA
# 二叉树找一个节点的后继节点
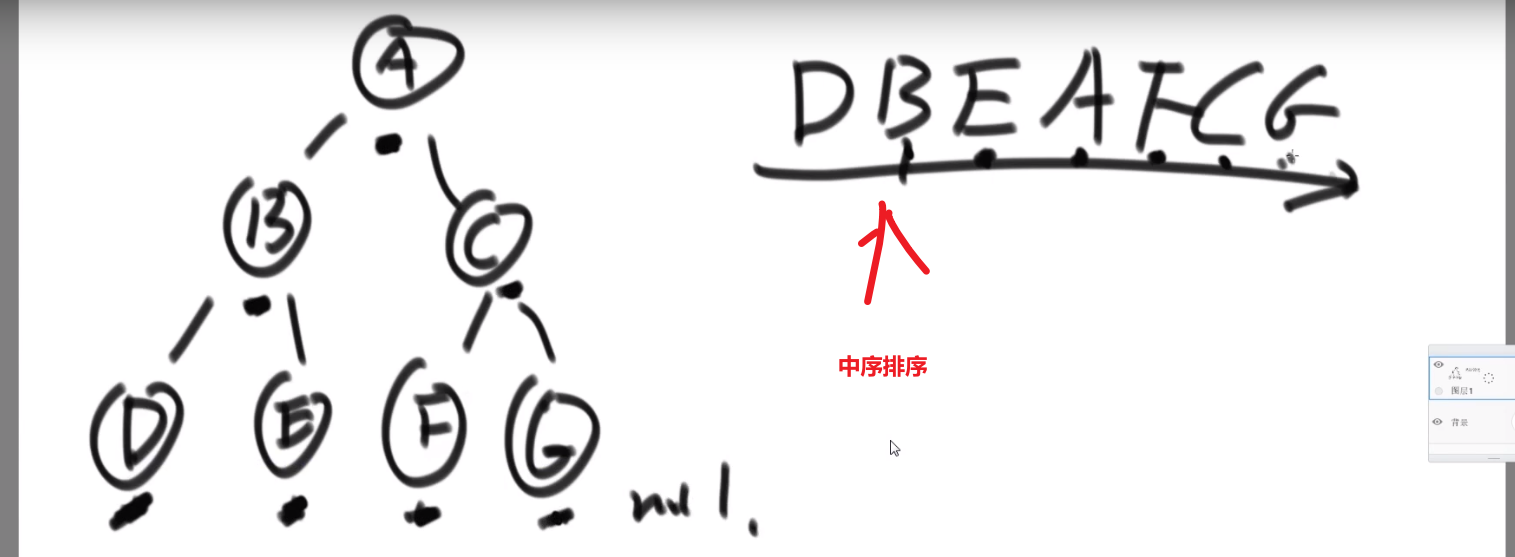
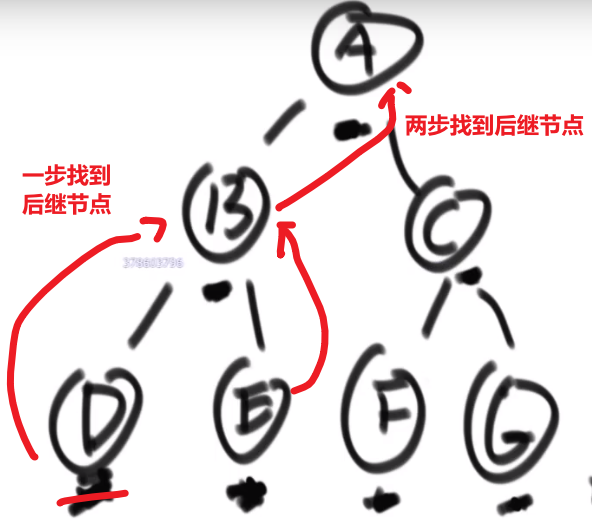
这里 ->D 的后继节点是 B,B 的后继节点是 E,E 的后继节点是 A,…G 的后继节点是 null
也就是中序排序中的一个节点后一个节点
同理,前驱节点就是后继节点反过来–> 中序排序的一个节点的前一个节点
题目:
我们之前做法可能就是遍历一下然后把所有的按照中序排好存到一个 set 里面,然后看节点后面的节点是什么就行,但是这样会耗空间因为有那个 set, 我们这里有很好的解法:
我们这里每个节点都有 parent 指针指向他的 parent, 所以没有必要像之前的做法
我们完全可以让那个节点他的 parent 指针找到对应的后继节点就行了
- 假设我们节点是在第三层然后他的 parent 也就是他的后继节点在第二层,那么只需要走一步就行了
- 假设我们节点是在第三层然后他的 parent 的 parent 也就是他的后继节点在第一层,那么只需要走两步就行了
还有各种可能,或许不是通过 parent 等等等,看代码!!!
所以,假设我们节点和他的后继节点之间的距离是 k, 那么我们可以有个 O (k) 时间复杂度的解法
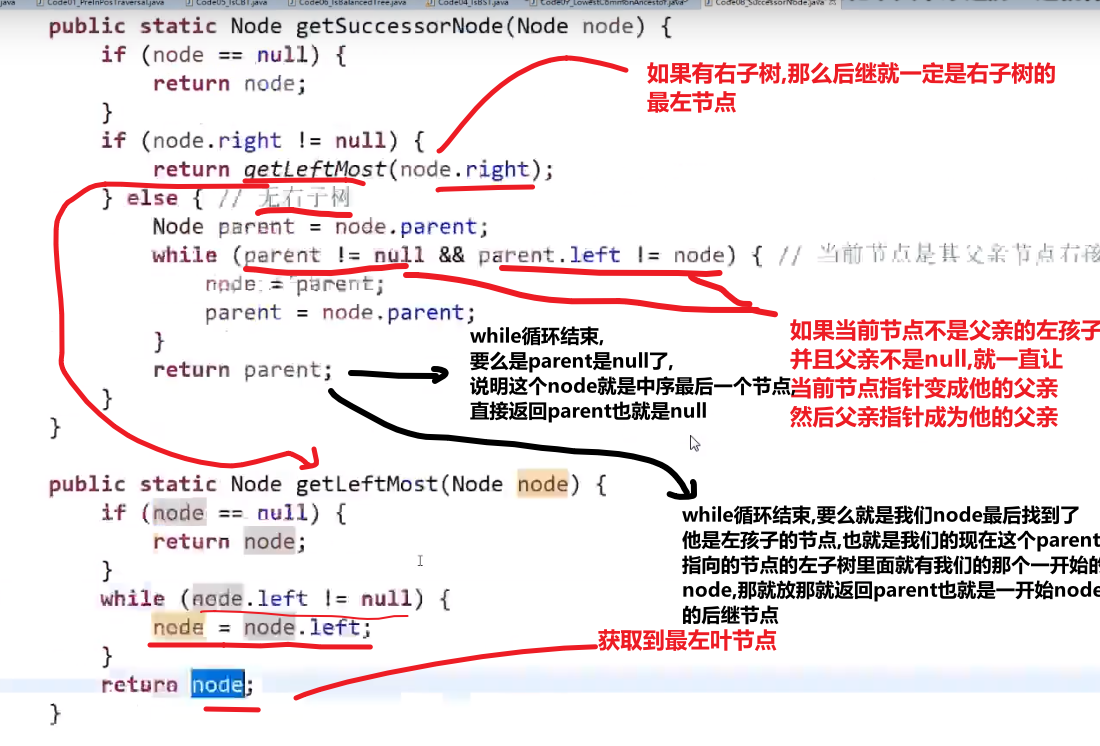
比如说给了个节点 X 找后继节点,有几种情况:
-
X 有右子树的时候,那么右子树的最左的 leaf 节点就是这个 X 的后继节点 (因为中序遍历,搞完 X 就去的右子树,他的右子树会先去搞他的左子树,等等等)
-
X 没有右子树,那么就会看 parent 然后看是不是我父亲的左孩子
- 如果是,那么这个父亲就是我们的后继节点
- 如果不是,那就继续往上看,一直看是头还不是,那就代表我们这个 X 是整颗数最右的叶节点,中序排序最后一个节点,没有后继节点,返回 null
- 如果不是,那就继续往上看,一直看是为止,此时那个父亲 (我们这个是左孩子了) 就是我们的 X 的后继节点
这是因为对于我们 Y 节点来说,我们的 X 就是 Y 的左子树最右的叶节点,也就是中序排序中他前面的那个节点 (打印完 X 就打印 Y)
# 二叉树的序列化和反序列化
就是我们这颗树的结构以及他的值都能对应一个字符串,这样我们可以序列化 (内存变成字符串), 然后接着反序列化 -> 字符串还原出来之前那棵树的结构以及值
好几种做法
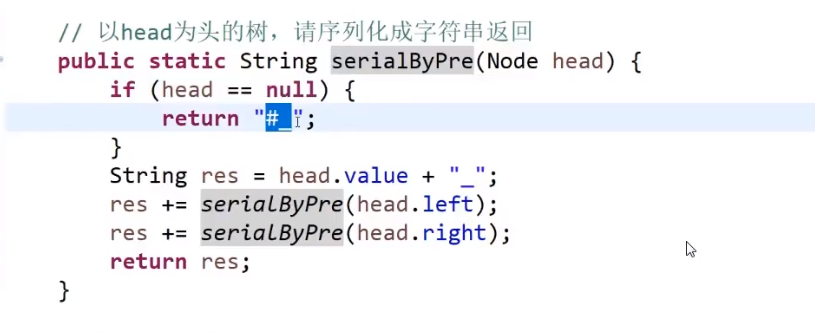
- 先序
序列化:
可以看出不一样,easy
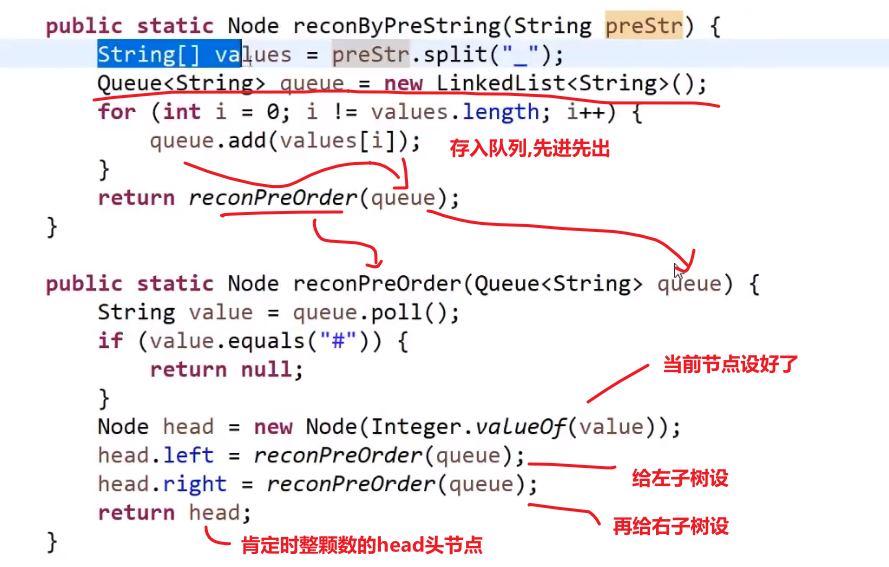
反序列化:
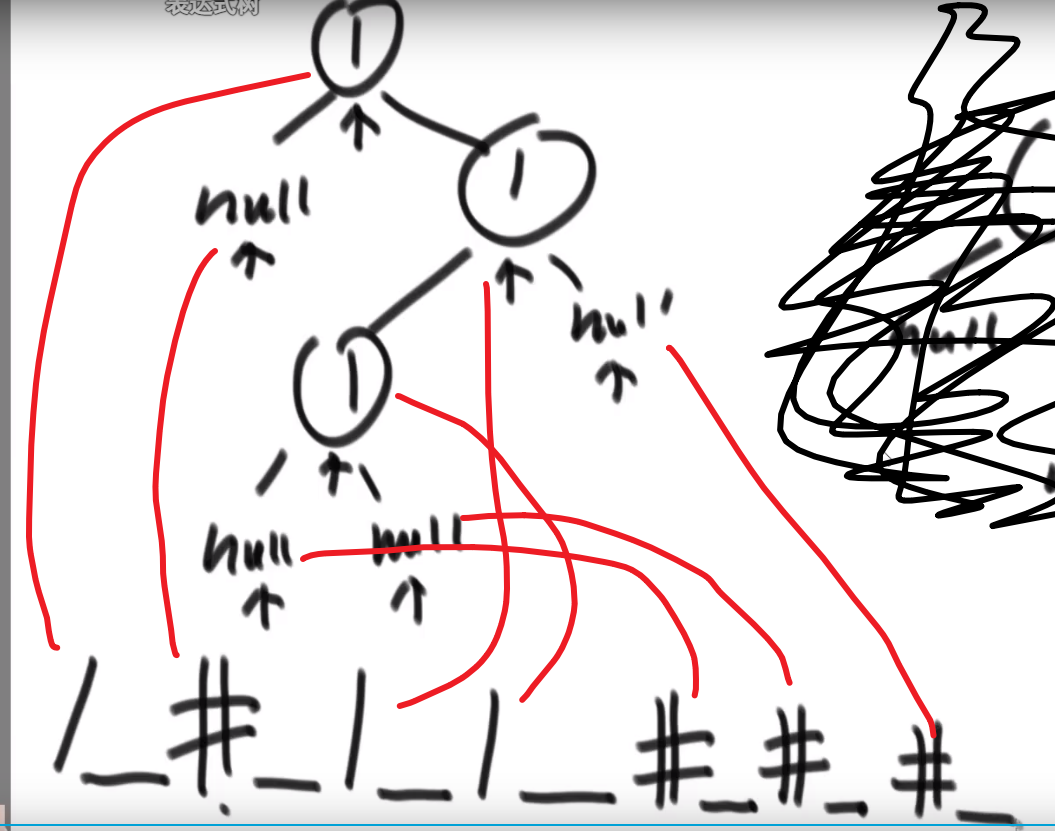
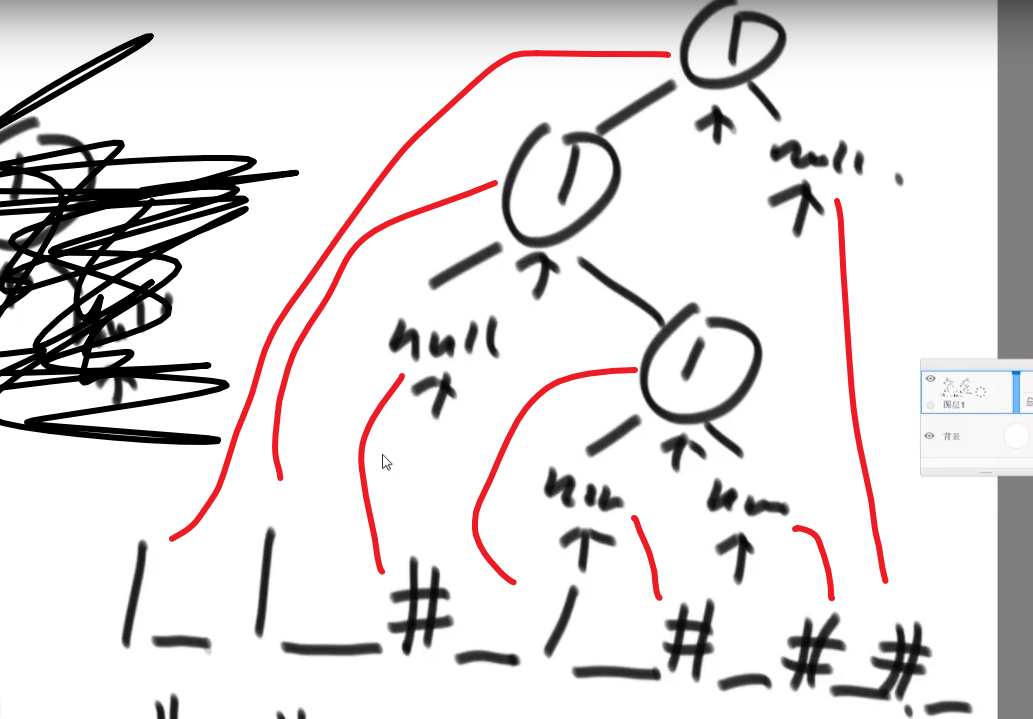
- 因为我们序列化是用_作为每个数的结尾,我们可以把_之前的每一个数都存入存入数组中
- 当初按照先序序列化的,现在按照先序反序列化
- 然后读数组第一个值作为 head, 然后再看下一个数作为 head 的左边的节点,so on…
- 如果遇到一个 #代表 null, 我们返回上一层,看那一层的右节点,so on…
这不就递归嘛!
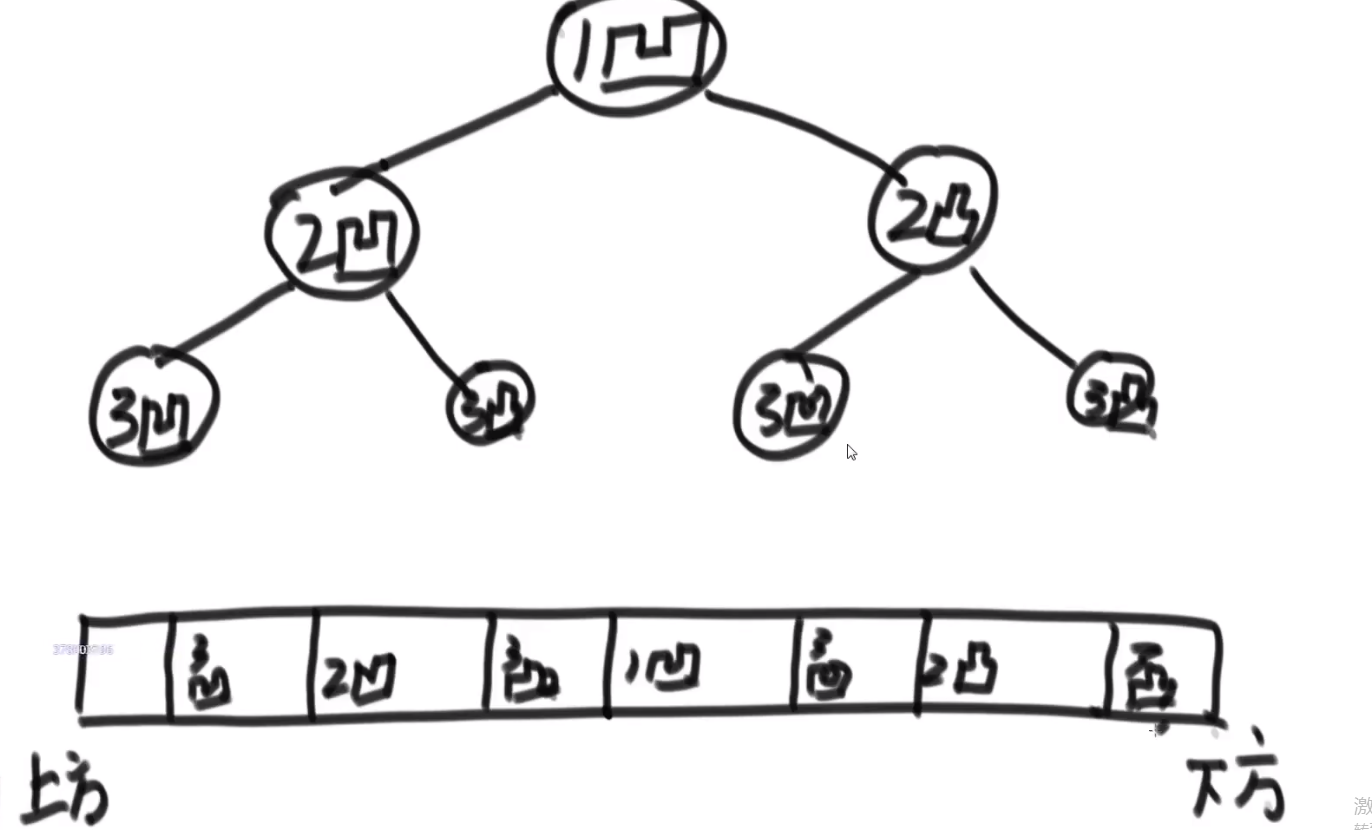
# 凹凸折痕
假设一张纸,给你个 N, 让你算出这张纸折叠 N 次,让你给出这张纸平摊后从上到下的折叠方向

整个就是二叉树
- 左子树都是凹折痕
- 右子树都是凸折痕
- 然后整个的头节点就是凹折痕
就是中序遍历,因为毕竟要求是从上到下的折叠方向也就是先把那个比如说 3 凹打印,然后 2 凹,3 凸等等等
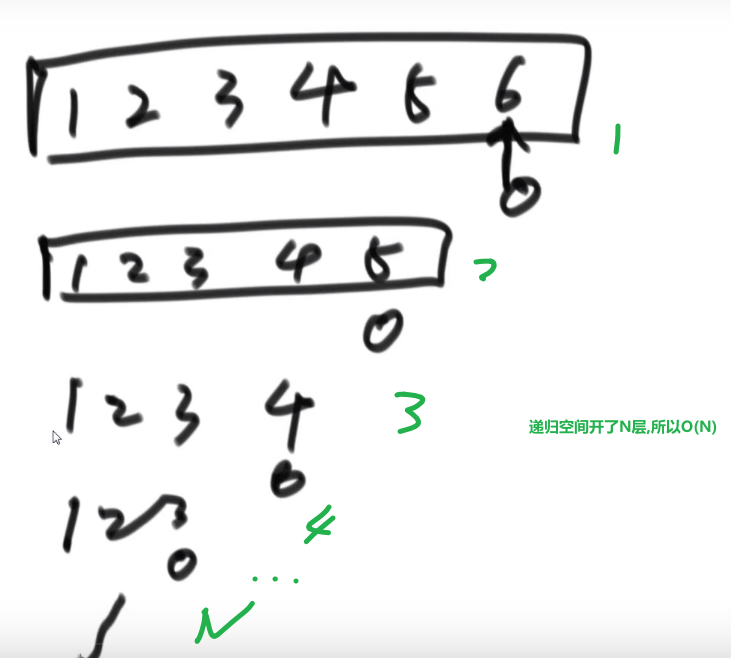
我们这里的空间复杂度是 O (N),N 是那个传进来的 N 值,因为我们最深 (递归) 打印到 N 层,所以很省空间
要是让我们暴力,可能会发现凹凸折痕是 2N-1 个,然后我们就挨个存上面的,然后挨个打印,那么空间复杂度就到了 O (2N) 级别了
我们这里直接递归,最多就是空间复杂度是 O (N), 因为我们最多深入到 N 层,之后返回就会挨个清空,之后要是还再深入也还是用我们之前清空的空间,也就最多 O (N) 空间复杂度
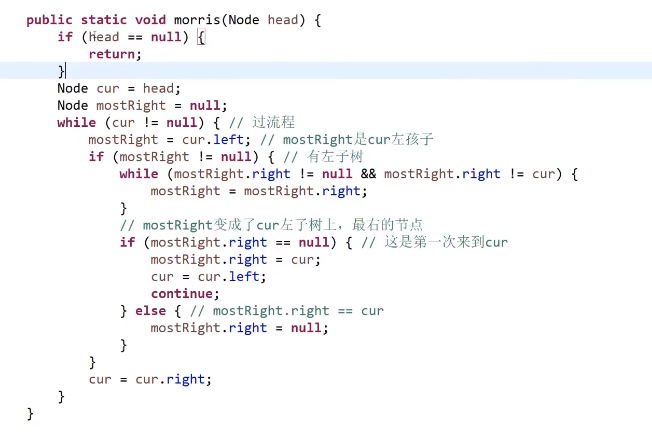
# 二叉树的 Morris 遍历
Morris 遍历,每个有左子节点的节点都会被访问两次,没有左子节点的只会被访问一次
时间复杂度就是 O (N), 因为每一个节点都最多被访问两次所以其实就是 O (n)(具体看视频)
空间复杂度就是 O (1), 就用了那几个指针
# 先序遍历
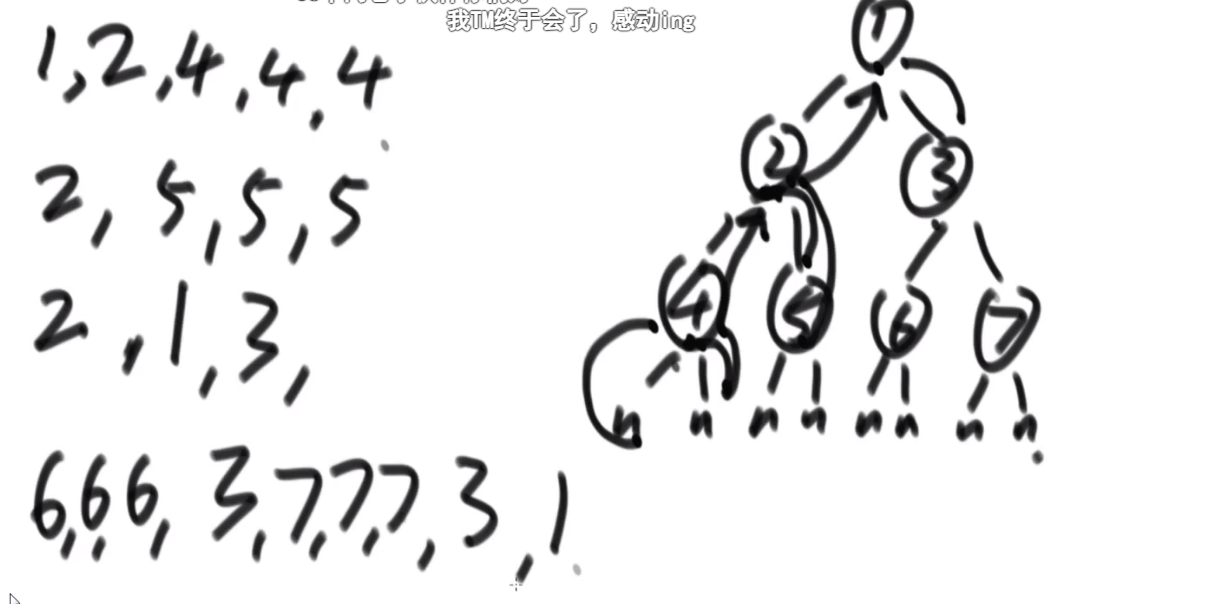
1
2 3
4 5 6 7
morris 序列 1 2 4 2 5 3 6 3 7
打印 morris 序列中第一次出现的元素就是先序遍历
(有左孩子即会出现两次)
先序 1 2 4 5 3 6 7
//第一次到达时,打印
public static void morrisPre(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
// 有左树,第二次到达时打印
System.out.print(cur.value + " ");
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
} else {
// 没有左树,第一次就打印
System.out.print(cur.value + " ");
}
cur = cur.right;
}
System.out.println();
}
# 中序遍历
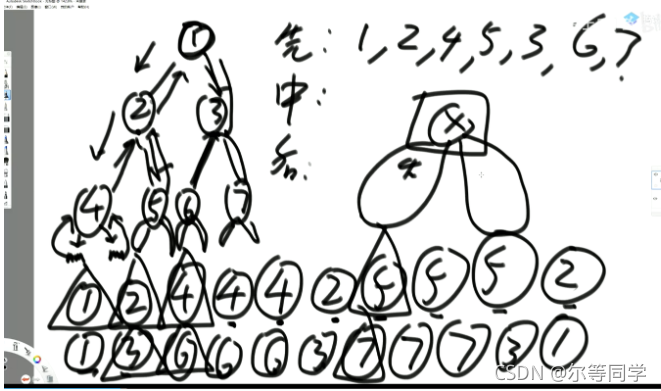
对于出现两次的元素,第二次打印,只出现一次的元素,第一次出现就打印
morris 序列 1 2 4 2 5 3 6 3 7
中序 4 2 5 1 6 3 7
public static void morrisIn(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
}
//只能到达一次的第一次打印,可以到达两次的第二次到达才打印
System.out.print(cur.value + " ");
cur = cur.right;
}
System.out.println();
}
# 后序遍历
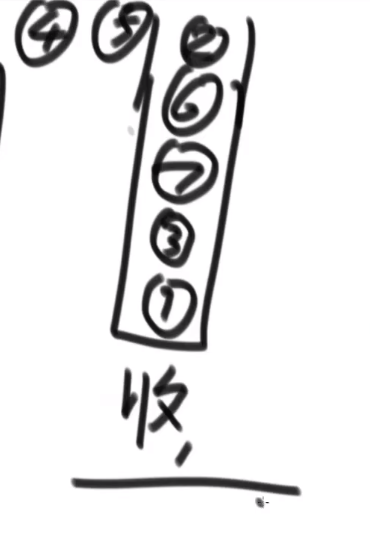
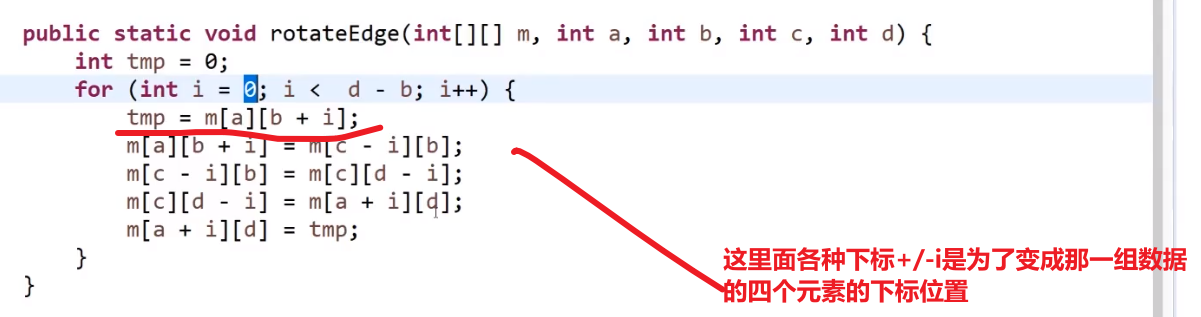
对于可以到达两次的元素,第二次回到该元素时,逆序打印右边界
整个树遍历后,逆序打印整棵树的右边界
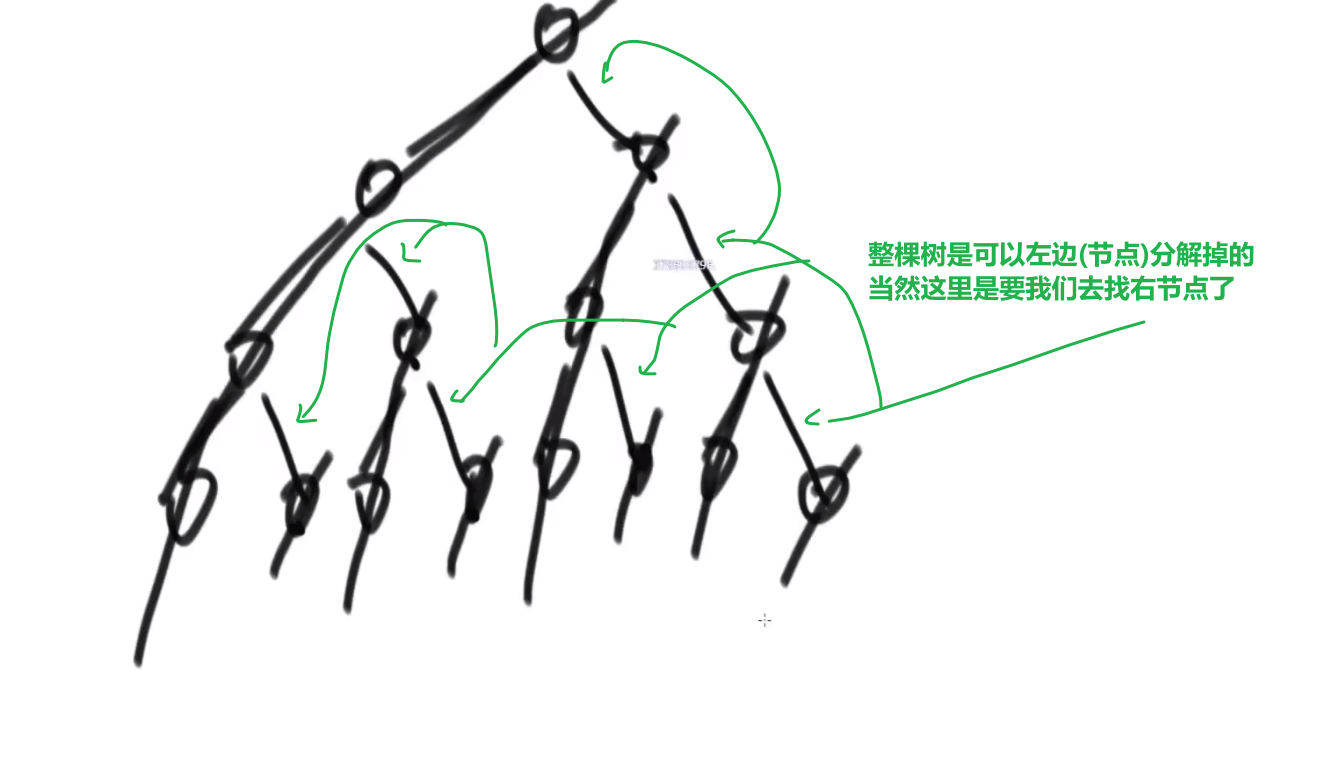
原理为:
一个树可以被右边界分解掉,由左往右,每次逆序打印其右边界,就是后序遍历
中途要求逆序打印,但 morris 要求 O(1)空间,即排除了使用额外空间的办法
可以使用反转链表来实现逆序打印
public static void morrisPos(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
//第二次回到该节点时,逆序打印此节点
printEdge(cur.left);
}
}
cur = cur.right;
}
// 结束之后,打印整个树的右边界
printEdge(head);
System.out.println();
}
//先链表反转,遍历后再反转回去
public static void printEdge(Node head) {
Node tail = reverseEdge(head);
Node cur = tail;
while (cur != null) {
System.out.print(cur.value + " ");
cur = cur.right;
}
reverseEdge(tail);
}
public static Node reverseEdge(Node from) {
Node pre = null;
Node next = null;
while (from != null) {
next = from.right;
from.right = pre;
pre = from;
from = next;
}
return pre;
}
# 判断是否为二叉查找树
中序遍历为递增序列则为二叉查找树
使用 morris 遍历
public static boolean isBST(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
Integer pre= null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
}
// 如果上一个值大于等于当前值,则这个树一定不是 bst
if(pre !=null && pre>=cur.value ){
return false;
}
pre =cur.value;
cur = cur.right;
}
return true;
}
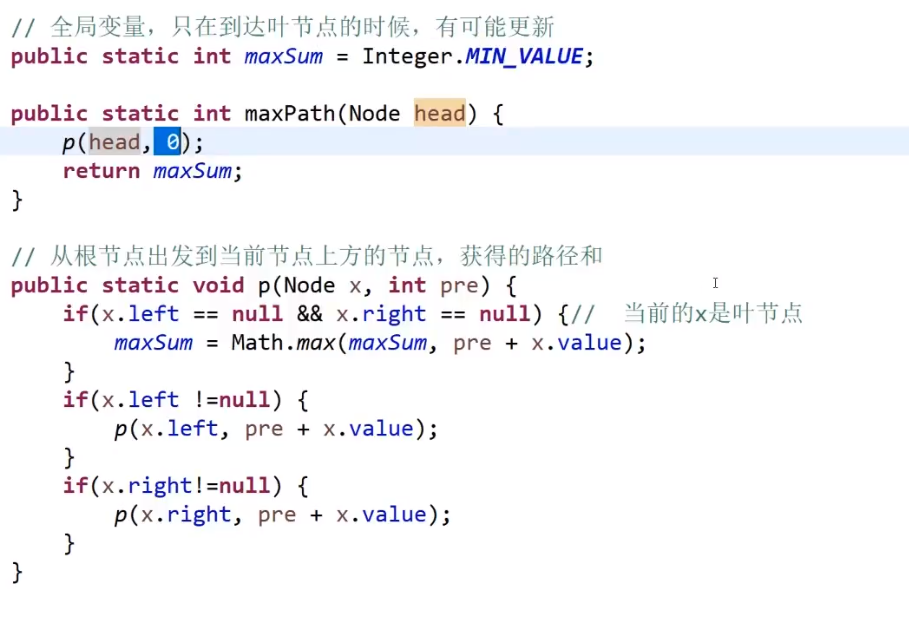
# 求二叉树最小高度
给定一棵二叉树的头节点 head
求以 head 为头的树中,最小深度是多少?
递归办法
public static class Node {
public int val;
public Node left;
public Node right;
public Node(int x) {
val = x;
}
}
public static int minHeight1(Node head) {
if (head == null) {
return 0;
}
return p(head);
}
// 返回x为头的树,最小深度是多少
// 使用递归求解
public static int p(Node x) {
if (x.left == null && x.right == null) {
return 1;
}
// 左右子树起码有一个不为空
int leftH = Integer.MAX_VALUE;
if (x.left != null) {
leftH = p(x.left);
}
int rightH = Integer.MAX_VALUE;
if (x.right != null) {
rightH = p(x.right);
}
return 1 + Math.min(leftH, rightH);
}
morris 办法
需要做到以下两点
每到一个节点,可以知道它的高度
每到一个节点,可以判断出是否为叶子节点
// 根据morris遍历改写
public static int minHeight2(Node head) {
if (head == null) {
return 0;
}
Node cur = head;
Node mostRight = null;
int curLevel = 0;
int minHeight = Integer.MAX_VALUE;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
int rightBoardSize = 1;
while (mostRight.right != null && mostRight.right != cur) {
// 由下往上的元素层数
rightBoardSize++;
mostRight = mostRight.right;
}
if (mostRight.right == null) { // 第一次到达
curLevel++;
mostRight.right = cur;
cur = cur.left;
continue;
} else {
// 第二次到达,需要减去rightBoardSize
if (mostRight.left == null) {
//此时到达叶节点,计算最小高度
minHeight = Math.min(minHeight, curLevel);
}
curLevel -= rightBoardSize;
mostRight.right = null;
}
} else {
// 只有一次到达
curLevel++;
}
cur = cur.right;
}
int finalRight = 1;
cur = head;
while (cur.right != null) {
finalRight++;
cur = cur.right;
}
// 单独去找一下最右部分的最小高度
if (cur.left == null && cur.right == null) {
minHeight = Math.min(minHeight, finalRight);
}
return minHeight;
}
# 图问题
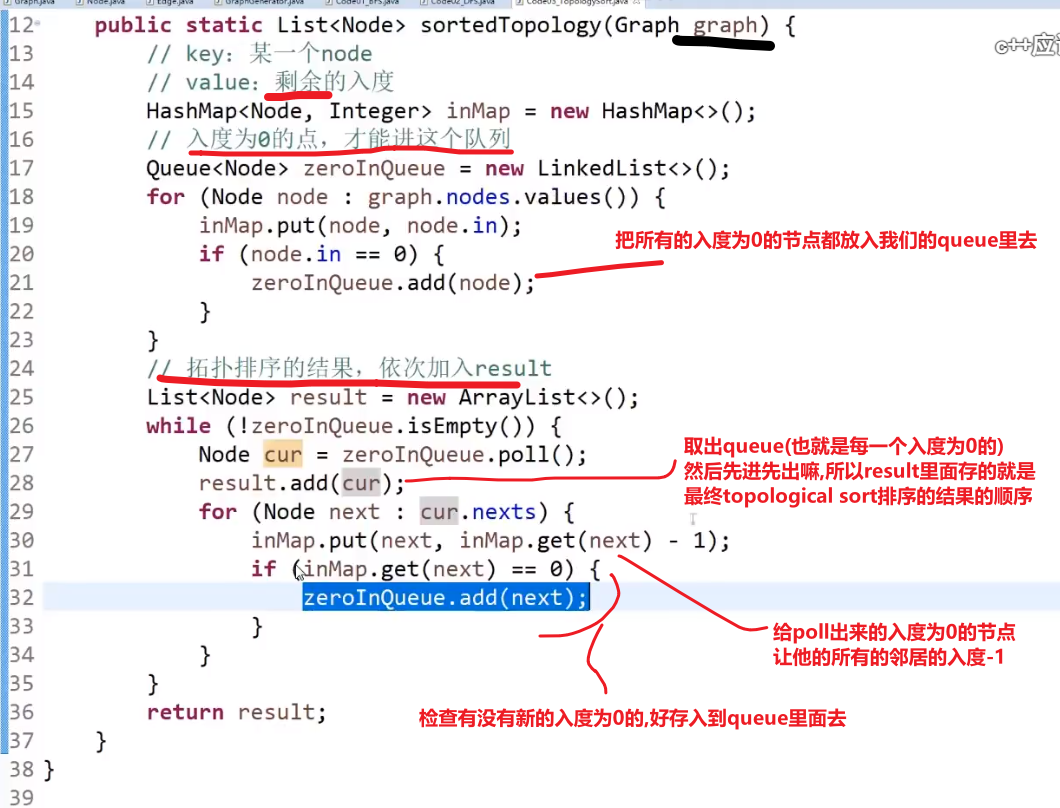
# 括扑排序算法 (topological sort)
- 适用于 Directed Acyclic Graph --> directed graph with no loops (无环–> 指的不只是自己指向自己的那种环,还包括多个节点形成的环)

比如说:工程中的依赖

注意不能拥有环,也就像工程中依赖之间不能循环依赖一样
对于上方的图,我们可以看到我们先需要 E 依赖,然后 C 依赖然后 D 依赖,然后 B 依赖,然后 A 依赖
问题例子:

解法:
- 我们首先入度为 0 的 (如果要拿 topological sort 来解答的话那就一定有这个)(一开始就是 A 节点)
这个节点就相当于是 (此时) 必须先要有的依赖,然后其他的依赖才可以设起来
-
接着把这个节点以及他的 outward edge 都擦掉 (肯定只会有 outward, 因为我们找到的是入度为 0 的),
记得把这个节点保存啊,进行什么操作啊等等等
-
重复 1,2–> 因为我们上面把 A 以及他的 outward edge 都擦掉了,此时 B 就是入度为零的节点,等等等
最终的 topological sort 顺序就是:

注意如果有多个入度为 0 的节点,那随便哪一个都行,反正我们之后顺序一定不会产生需要依赖的在前面然后被依赖的那个在后面.
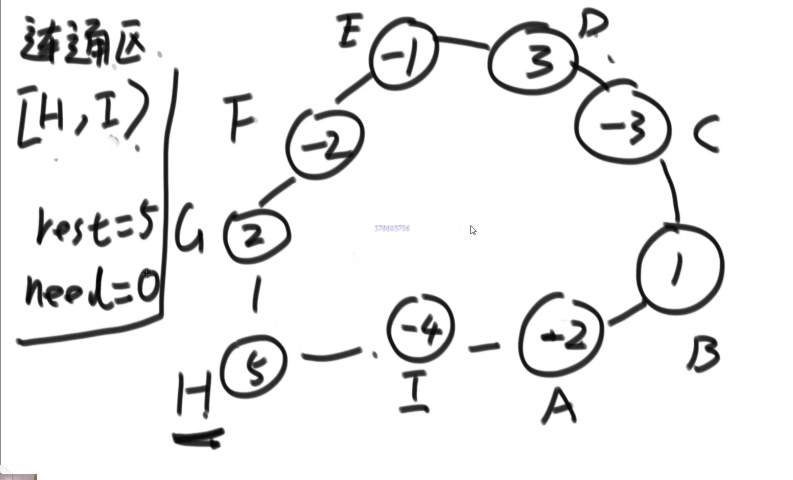
# 最小生成树以及相关算法 (和一些 terminologies)
关于图的几个概念定义:
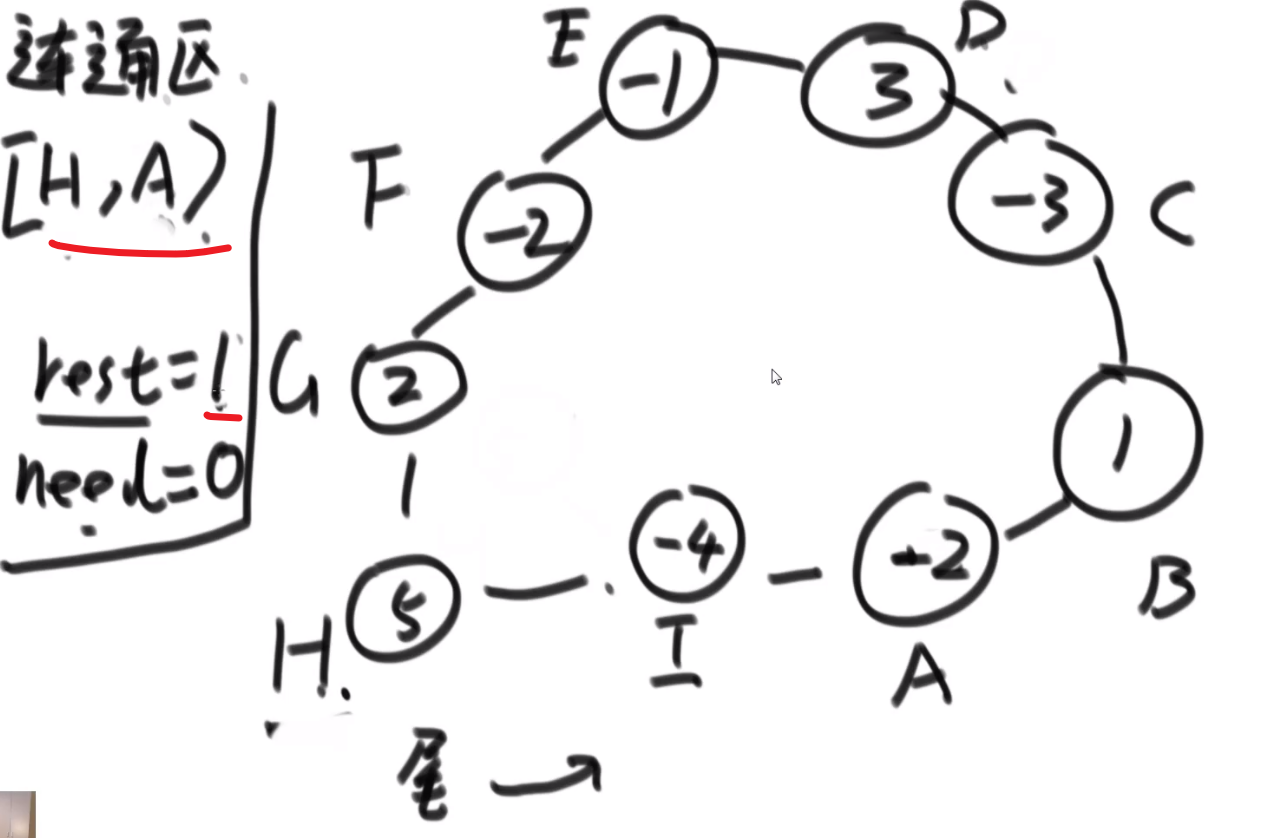
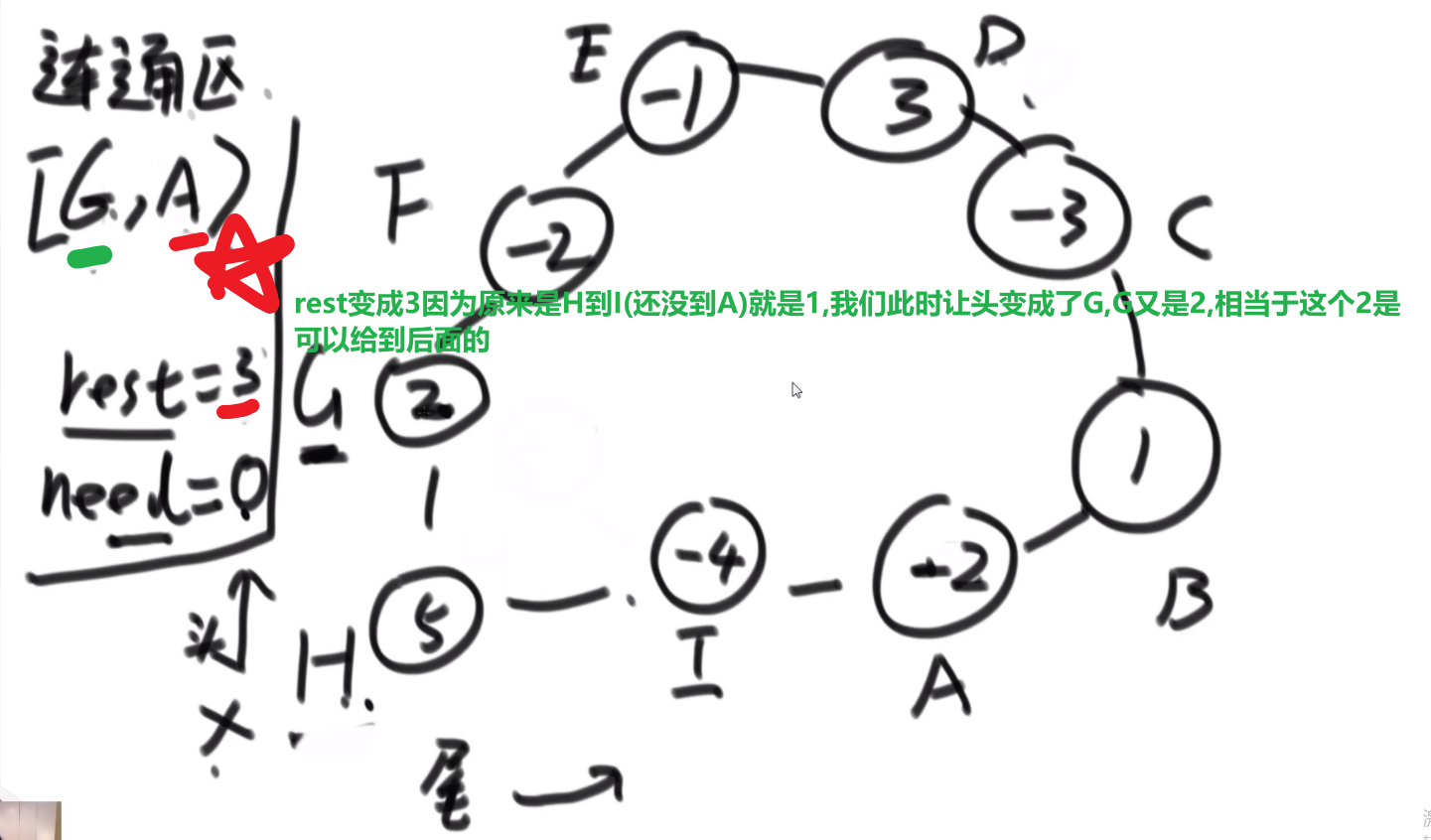
** 连通图:** 在无向图中,若任意两个顶点 vivi 与 vjvj 都有路径相通,则称该无向图为连通图。
** 强连通图:** 在有向图中,若任意两个顶点 vivi 与 vjvj 都有路径相通,则称该有向图为强连通图。
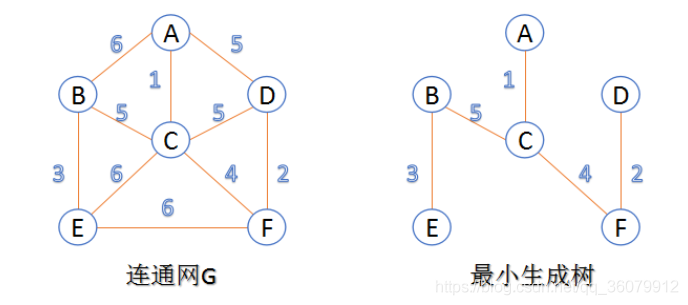
** 连通网:** 在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
** 生成树:** 一个连通图的生成树是指一个连通子图,它含有图中全部 n 个顶点,但只有足以构成一棵树的 n-1 条边。一颗有 n 个顶点的生成树有且仅有 n-1 条边,如果生成树中再添加一条边,则必定成环。
** 最小生成树 (minimum weight spanning tree):** 在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
可以用 kruskal 或者 Prim 生成最小生成树
# Terminologies
# Definitions: Graph, Vertices, Edges
-
Define a graph G = (V, E) by defining a pair of sets:
- V = a set of vertices
- E = a set of edges
-
Edges:
- Each edge is defined by a pair of vertices
- An edge connects the vertices that define it
- In some cases, the vertices can be the same
-
Vertices:
- Vertices also called nodes
- Denote vertices with labels
-
Representation:
- Represent vertices with circles, perhaps containing a label
- Represent edges with lines between circles
-
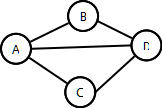
Example:
- V =
- E =
# Motivation
Many algorithms use a graph representation to represent data or the problem to be solved
Examples:
-
Cities with distances between
-
Roads with distances between intersection points
-
Course prerequisites
-
Network
-
Social networks
-
Program call graph and variable dependency graph
# Graph Classifications
-
There are seveal common kinds of graphs
- Weighted or unweighted
- Directed or undirected
- Cyclic or acyclic
-
Choose the kind required for problem and determined by data
-
We examine each below
# Kinds of Graphs: Weighted and Unweighted
Graphs can be classified by whether or not their edges have weights
- Weighted graph: edges have a weight
- Weight typically shows cost of traversing
- Example: weights are distances between cities
- Unweighted graph: edges have no weight
- Edges simply show connections
- Example: course prereqs
# Kinds of Graphs: Directed and Undirected
Graphs can be classified by whether or their edges are have direction
- Undirected Graphs: each edge can be traversed in either direction
- Directed Graphs: each edge can be traversed only in a specified direction
# Undirected Graphs
-
Undirected Graph: no implied direction on edge between nodes
-
The example from above is an undirected graph
-
In diagrams, edges have no direction (ie they are not arrows)
-
Can traverse edges in either directions
-
-
In an undirected graph, an edge is an unordered pair
-
Actually, an edge is a set of 2 nodes, but for simplicity we write it with parens
- For example, we write (A, B) instead of
- Thus, (A,B) = (B,A), etc
- If (A,B) ∈ E then (B,A) ∈ E
-
Formally: ∀ u,v ∈ E, (u,v)=(v,u) and u ≠ v
-
-
A node normally does not have an edge to itself
# Directed Graphs
-
Digraph: A graph whose edges are directed (ie have a direction)
-
Edge drawn as arrow
-
Edge can only be traversed in direction of arrow
-
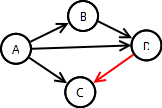
Example: E =
-
Examples: courses and prerequisites, program call graph
-
-
In a digraph, an edge is an ordered pair
- Thus: (u,v) and (v,u) are not the same edge
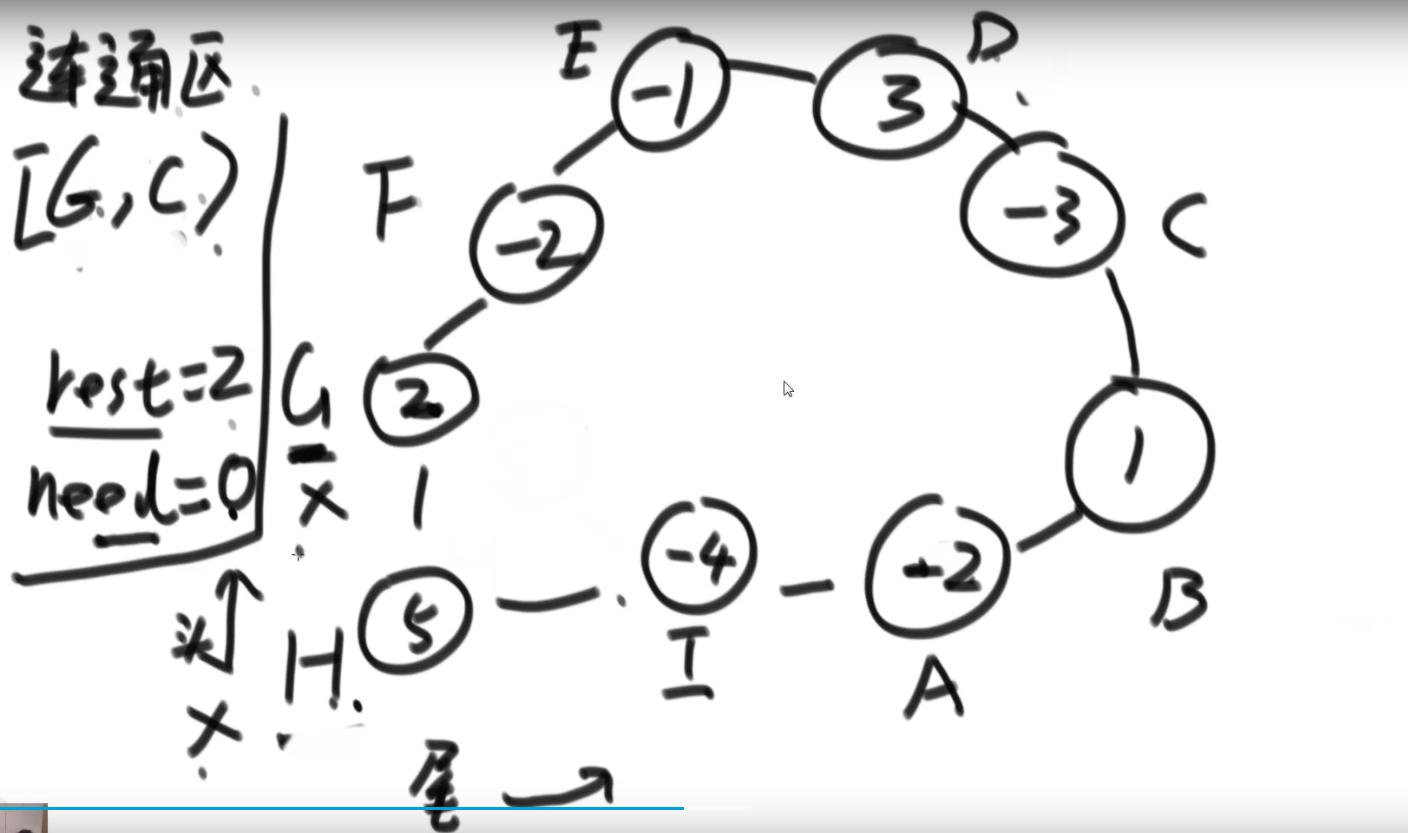
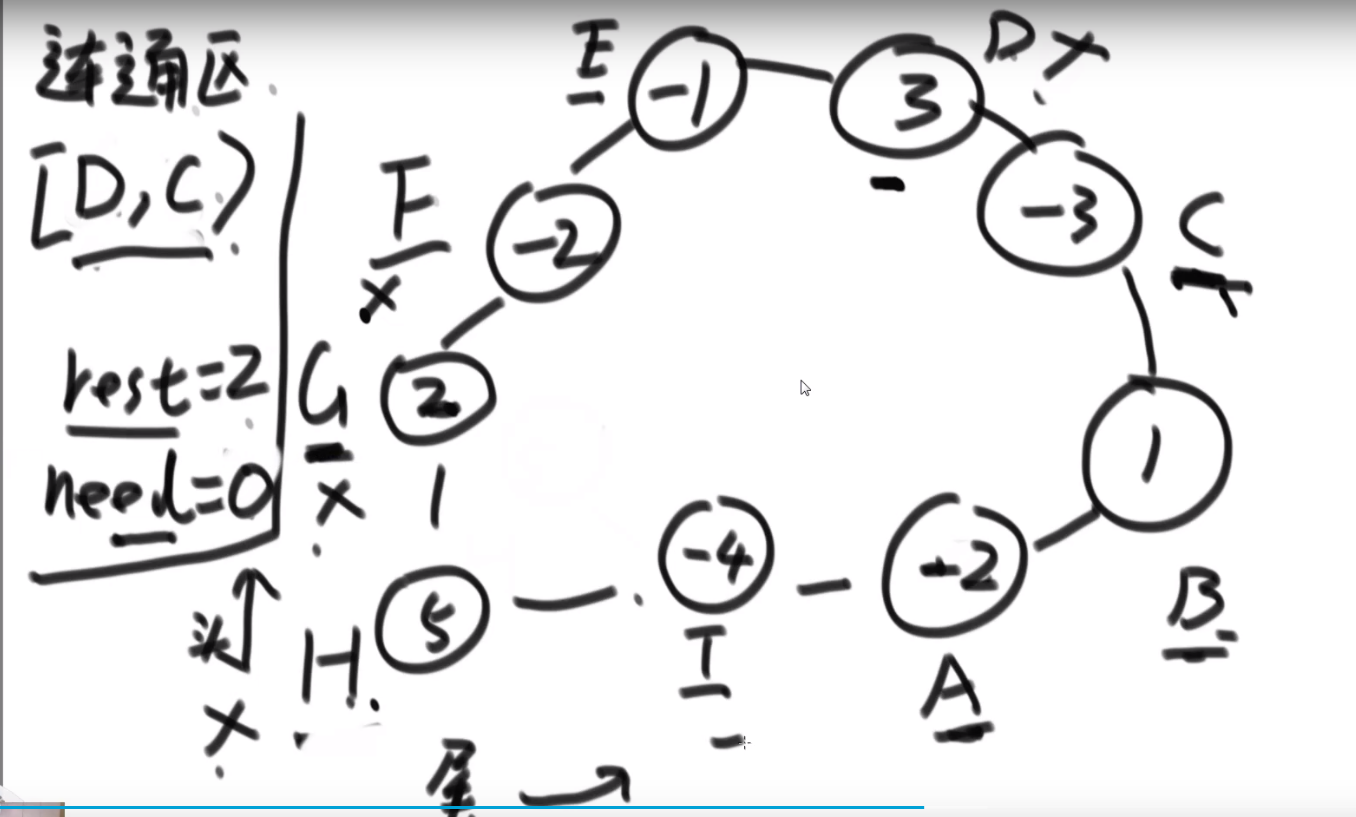
- In the example, (D,C) ∈ E, (C,D) ∉ E
- What would edge (B,A) look like? Remember (A,B) ≠ (B,A)
-
A node can have an edge to itself (eg (A,A) is valid)
# Subgraph
- If graph G=(V, E)
- Then Graph G’=(V’,E’) is a subgraph of G if V’ ⊆ V and E’ ⊆ E and
# Degree of a Node
-
The degree of a node is the number of edges the node is used to define
-
In the example above:
- Degree 2: B and C
- Degree 3: A and D
- A and D have odd degree, and B and C have even degree
-
Can also define in-degree and out-degree
- In-degree: Number of edges pointing to a node
- Out-degree: Number of edges pointing from a node
# Graphs: Terminology Involving Paths
-
Path: sequence of vertices in which each pair of successive vertices is connected by an edge
-
Cycle: a path that starts and ends on the same vertex
-
Simple path: a path that does not cross itself
- That is, no vertex is repeated (except first and last)
- Simple paths cannot contain cycles
-
Length of a path: Number of edges in the path
- Sometimes the sum of the weights of the edges
# Cyclic and Acyclic Graphs
-
A Cyclic graph contains cycles
Example: roads (normally)
-
An acyclic graph contains no cycles
Example: Course prereqs!
# Connected and Unconnected Graphs and Connected Components
-
An undirected graph is connected if every pair of vertices has a path between it
- Otherwise it is unconnected
-
An unconnected graph can be broken in to connected components
-
A directed graph is strongly connected if every pair of vertices has a path between them, in both directions
# Trees and Minimum Spanning Trees
- Tree: undirected, connected graph with no cycles
- Spanning tree: a spanning tree of G is a connected subgraph of G that is a tree
- Minimum spanning tree (MST): a spanning tree with minimum weight
- Spanning trees and minimum spanning tree are not necessarily unique
- We will look at two famous MST algorithms: Prim’s and Kruskal’s
# Data Structures for Representing Graphs
- Two common data structures for representing graphs:
- Adjacency lists
- Adjacency matrix
# Adjacency List Representation
-
Each node has a list of adjacent nodes
-
Example (undirected graph):
-
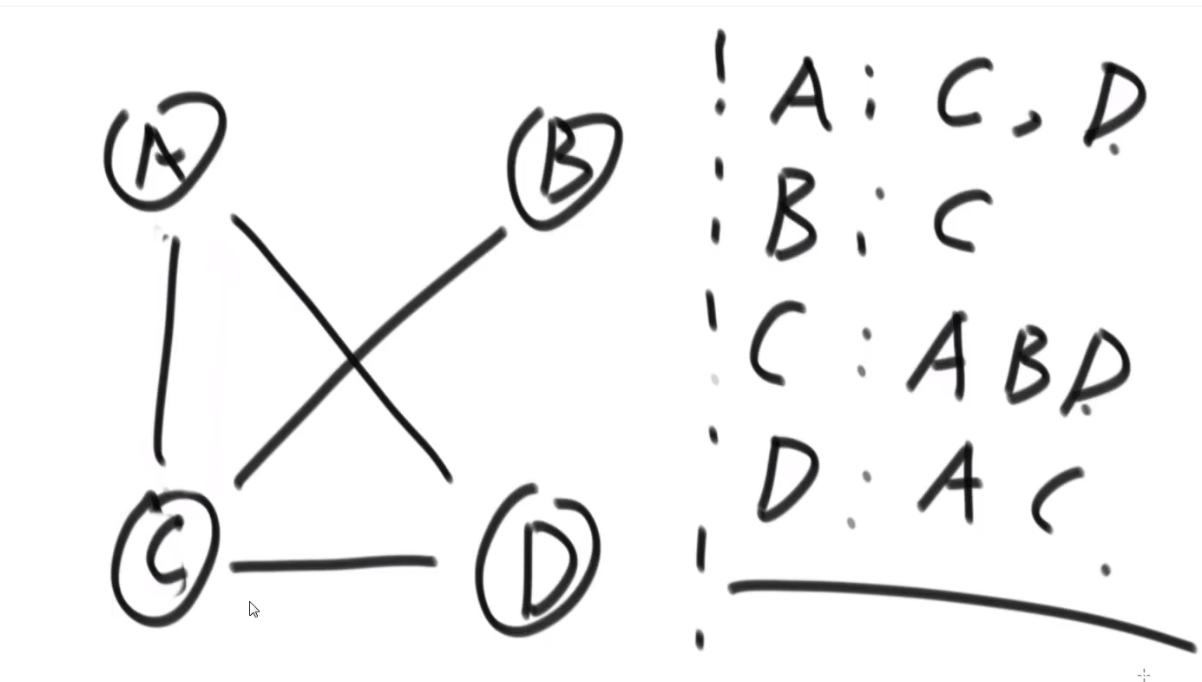
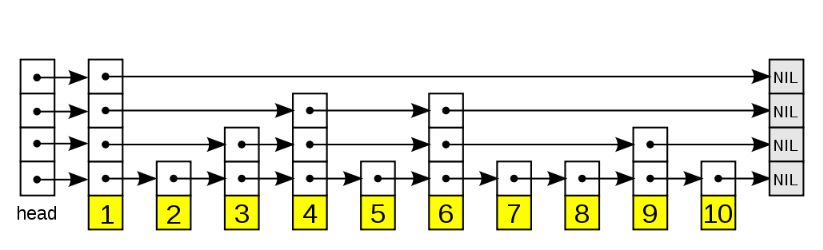
A: B, C, D
-
B: A, D
-
C: A, D
-
D: A, B, C
-
-
Example (directed graph):
-
A: B, C, D
-
B: D
-
C: Nil
-
D: C
-
-
Weighted graph can store weights in list
-
Space: Θ(V + E) (ie |V| + |E|)
-
Time:
- To visit each node that is adjacent to node u: Θ(degree(u))
- To determine if node u is adjacent to node v: Θ(degree(u))
# Adjacency Matrix Representation
-
Adjacency Matrix: 2D array containing weights on edges
- Row for each vertex
- Column for each vertex
- Entries contain weight of edge from row vertex to column vertex
- Entries contain ∞ (ie Integer’last) if no edge from row vertex to column vertex
- Entries contain 0 on diagonal (if self edges not allowed)
-
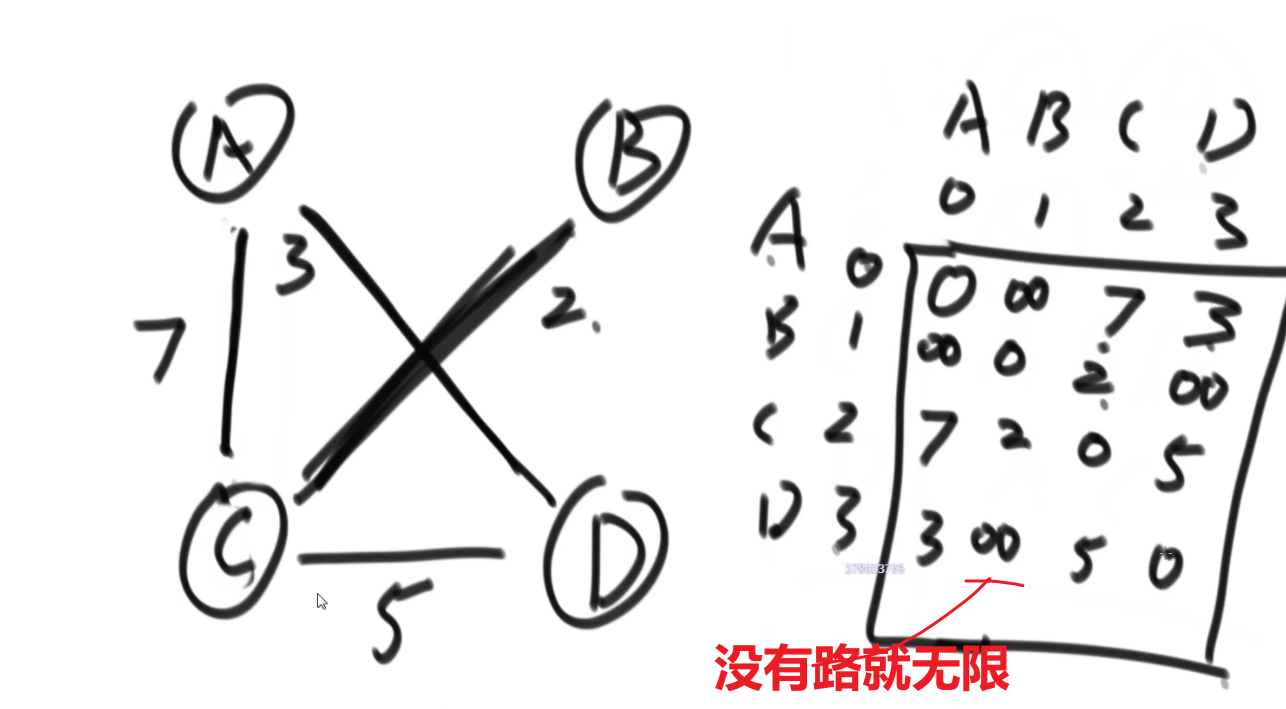
Example undirected graph (assume self-edges not allowed):
A B C D A 0 1 1 1 B 1 0 ∞ 1 C 1 ∞ 0 1 D 1 1 1 0 -
Example directed graph (assume self-edges allowed):
A B C D A ∞ 1 1 1 B ∞ ∞ ∞ 1 C ∞ ∞ ∞ ∞ D ∞ ∞ 1 ∞ -
Can store weights in cells
-
Space: Θ(V2)
-
Time:
- To visit each node that is adjacent to node u: Θ(V)
- To determine if node u is adjacent to node v: Θ(1)
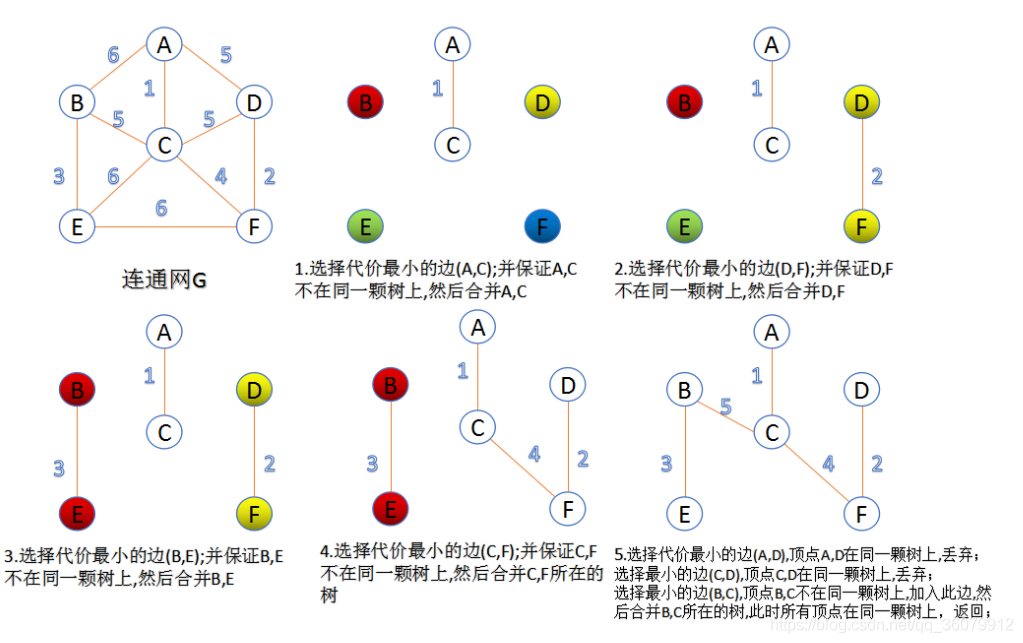
# kruskal 算法(K 算法) 适用范围:要求无向图 (undirected graph/graph)
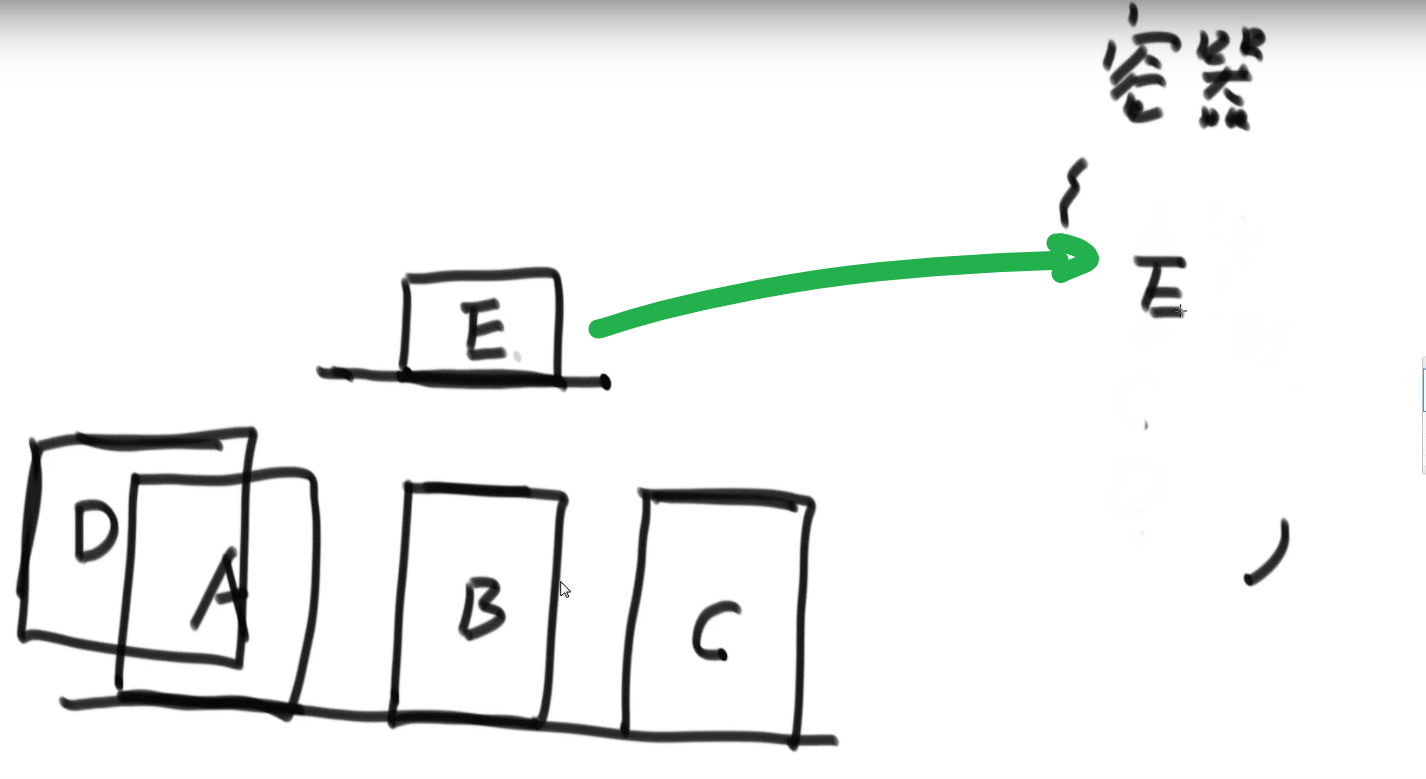
此算法可以称为 “加边法”,初始最小生成树边数为 0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
-
可以想象一开始每个点就是一个集合 (甚至可以想象是整张 graph 是 n 棵树组成的森林然后把图中的 n 个顶点看成独立的 n 棵树组成的森林)
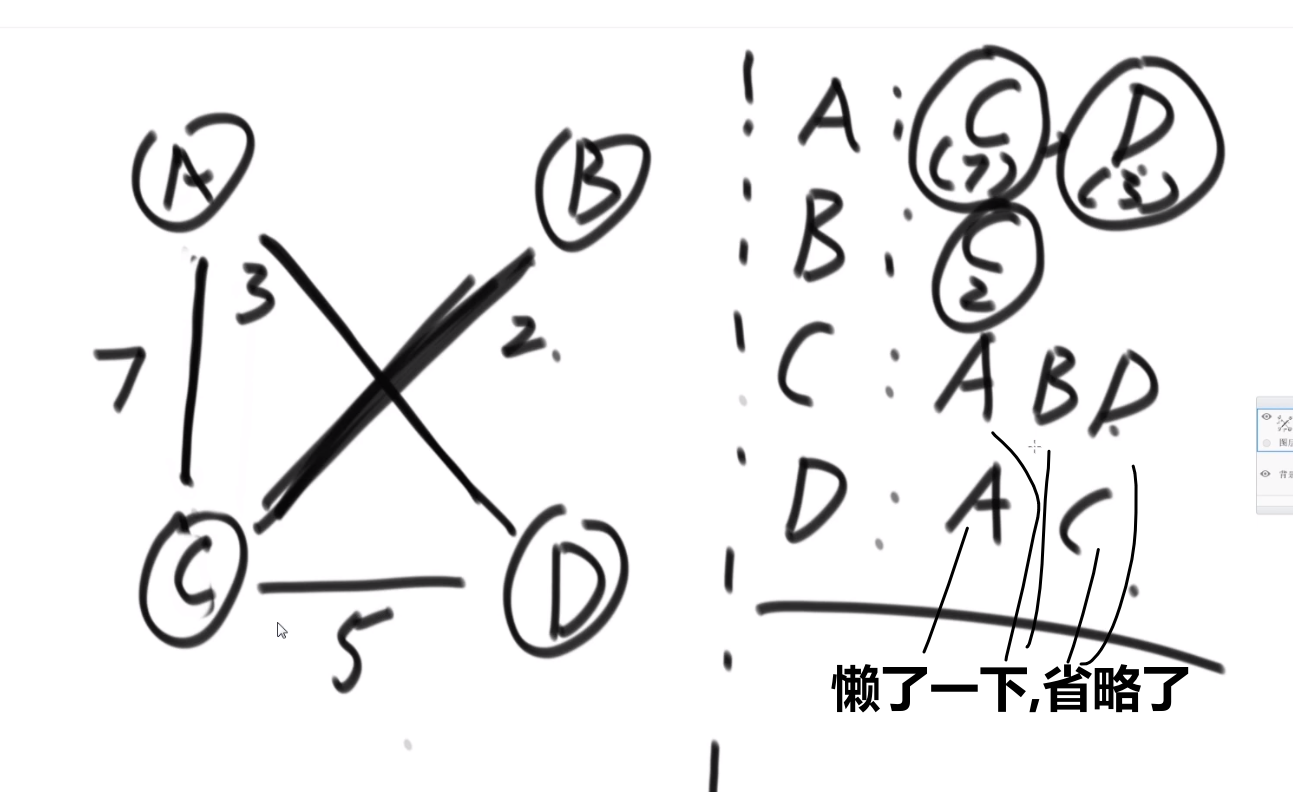
-
我们接着按照图中所有的 edges 最小 weight 的那个开始 (升序一个一个来)
-
然后对于那个 edge, 我们检查他的 u (from) 节点和 v (to) 节点是不是在一个集合中 (也就是这个边连接的点是不是已经是同一棵树了还是两颗不同的树)
-
如果不在我们就把这个 edge 加入到我们最小生成树里面,然后把 u 和 v 放到一个集合里面去,
------> 当前的边进入最小生成树的集合中不会形成环
-
如果在我们不会把 edge 加入到我们的最小生成树里面,(这说明他们之间已经有路 (path) 了,不需要这个 weight 更高的路)
------> 当前的边进入最小生成树的集合中会形成环
-
-
然后当我们的 edges 都处理完,说明我们最小生成树就有了
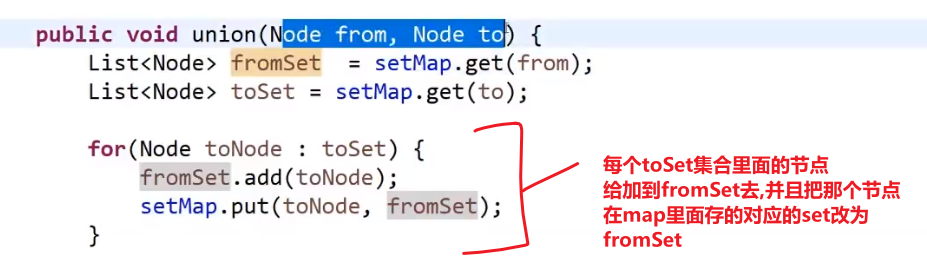
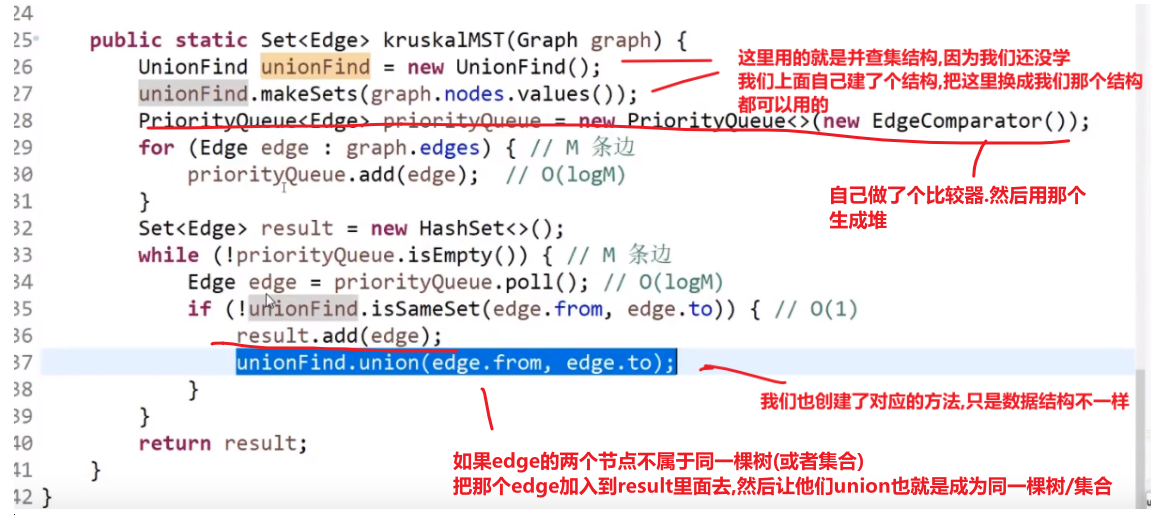
这种需要并查集结构才好实现–> 我们这里只是模拟,之后会学到并查集
# Prim 算法(P 算法)适用范围:要求无向图 (undirected graph/graph)
此算法可以称为 “加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点 s 开始,逐渐长大覆盖整个连通网的所有顶点。
-
任意一个节点开始
-
我们搜索他的 edges, 然后找那个最小 weight 的,看那个 edge 连着的节点是不是已经访问过 (加入到 set 了)
- 已经访问过,那就继续看下一个最小 weight 的 edge 连接的节点
- 没有访问过,那就把这个节点存入到 set 里面去,并记录这个 edge, 接着把这个新纪录到 set 里面去的节点所有的 edges 放入到小根堆里面,继续找出现在所有的解锁的小根堆里面的有的 edges 按照我们给的比较器规则会找出那个当前最小的 weight 的那个 edge
重复,so on…
(这期间可能会把同一个 edges 多次存入到小根堆,这个没事,因为之后我们取出来都会看那个 toNode 是不是已经是在 set 了,如已经在了那个 edge 也不会被处理) 结果就是找到最小生成树,result 存的都是一个一个最小生成树的 edges
所以要是问题只是告诉你只是一个连通的,那就没必要那个 for 循环
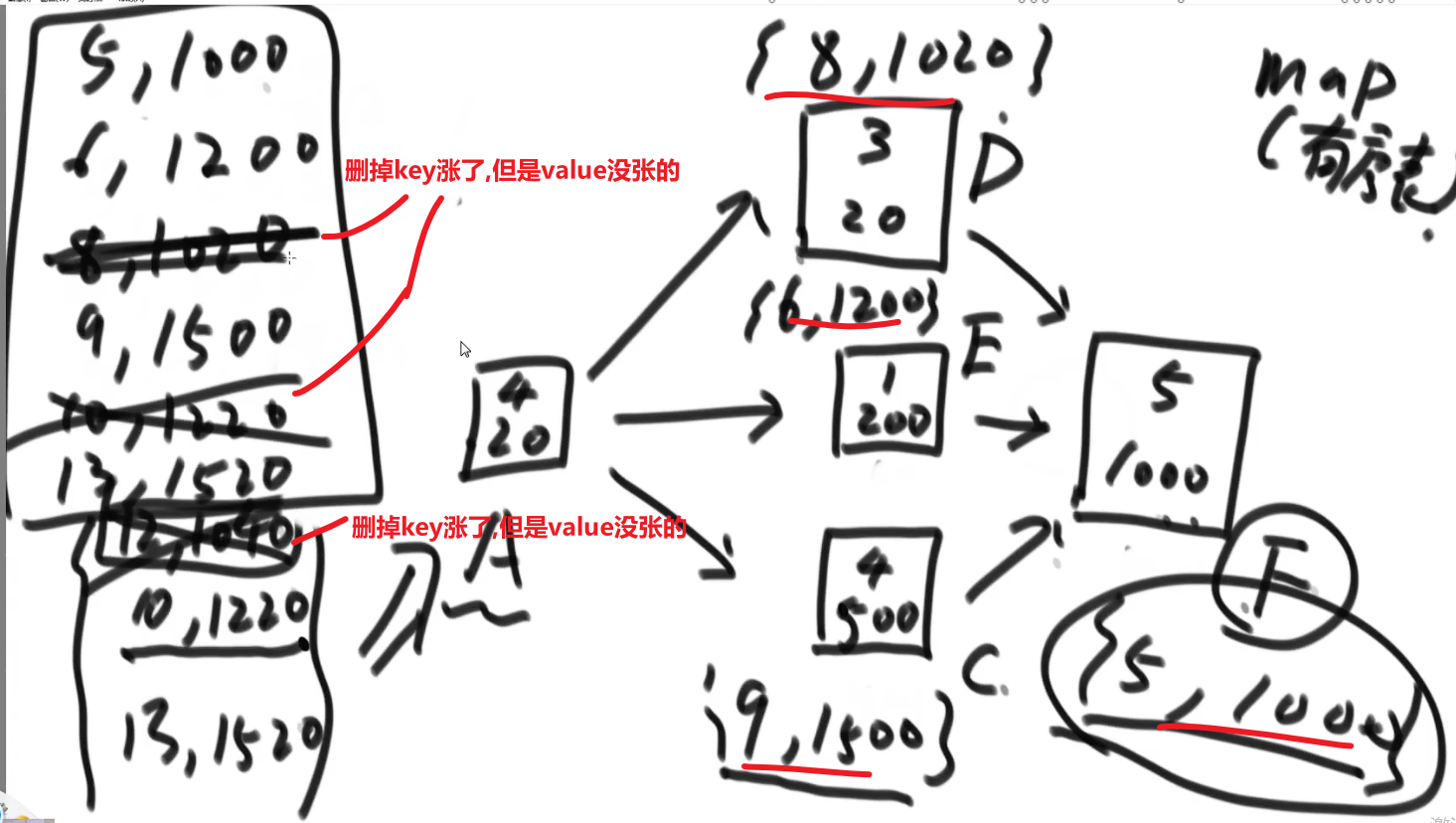
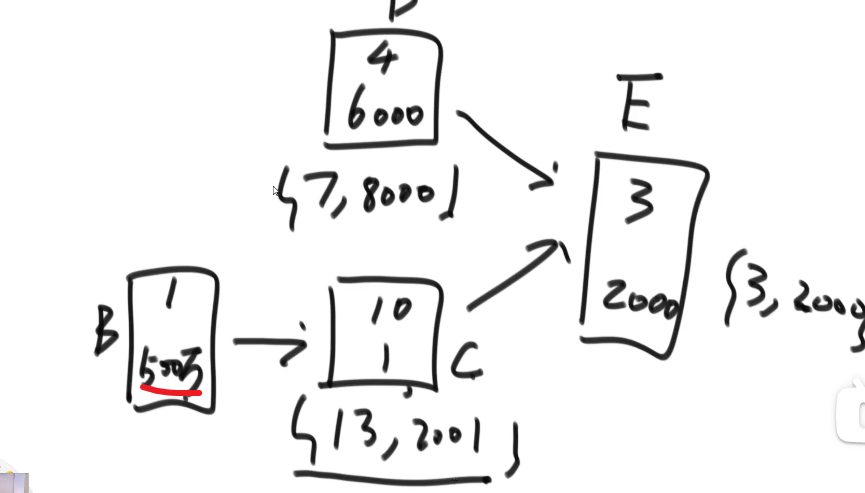
# 迪杰斯特拉算法
求解单元点的最短路径问题:给定带权 (weight) 有向图 G 和源点 v,求 v 到 G 中其他顶点的最短路径
限制条件:图 G 中不可以存在 negative cycle (肯定不行), 也不可以有 negative weight (貌似)
The algorithm creates a tree of shortest paths from the starting vertex, the source, to all other points in the graph.
比如说:

要是有 A 节点无法抵达的节点,那么之间的距离就是无限
迪杰斯特拉算法总共就干了两件事:
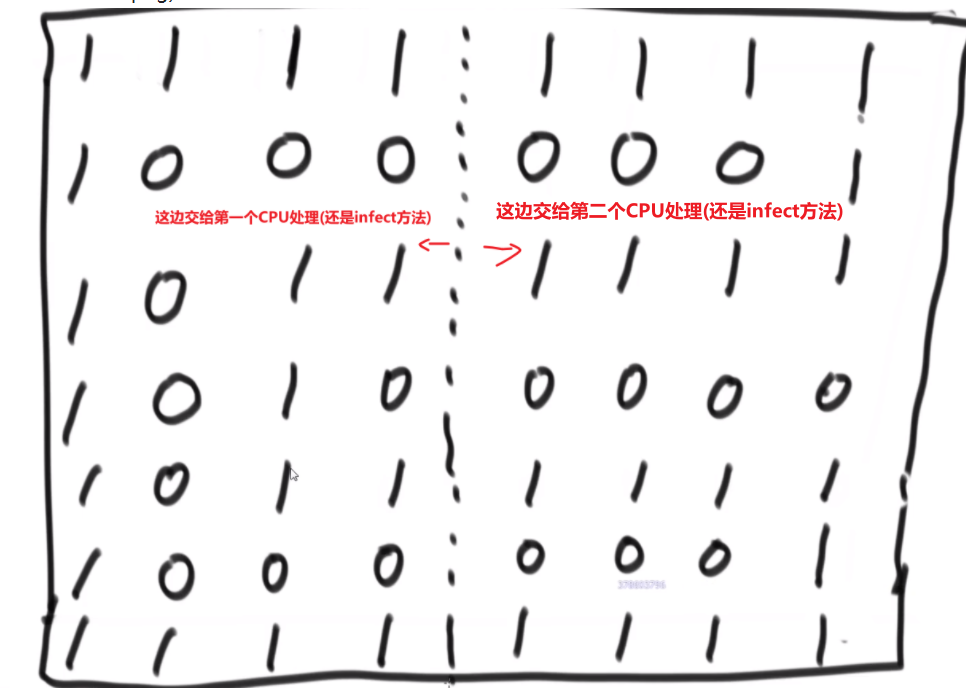
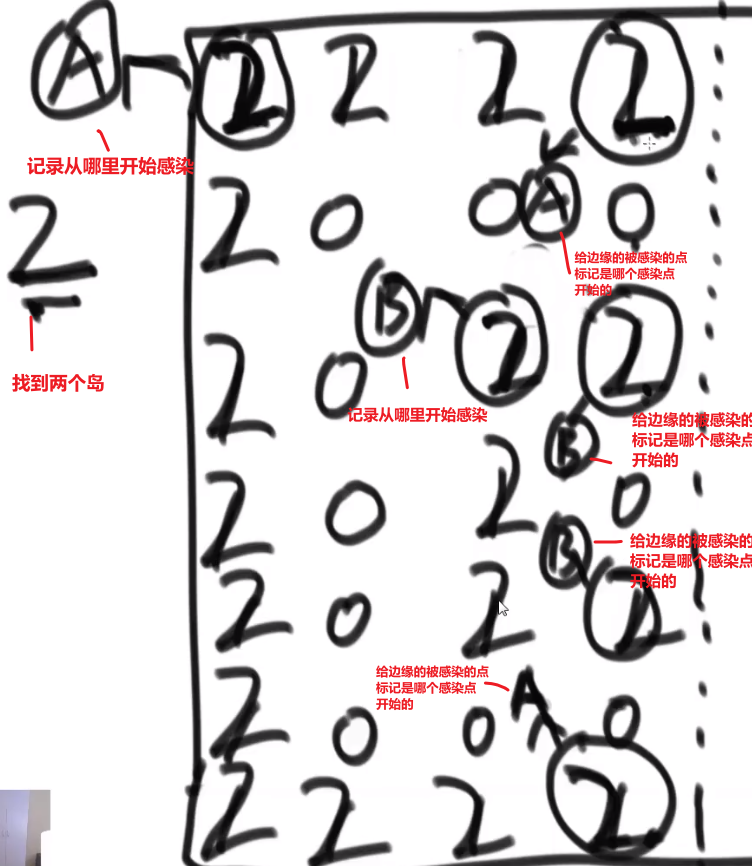
【1】不断运行广度优先算法找可见点,计算可见点到源点的距离长度
【2】从当前已知的路径中选择长度最短的将其顶点加入 S 作为确定找到的最短路径的顶点。
有点贪心的意思,每次都锁死一个值,这也为什么不能有 negative weight 因为要是有了那肯定会让之前已经锁死的边的值变,那就不对了
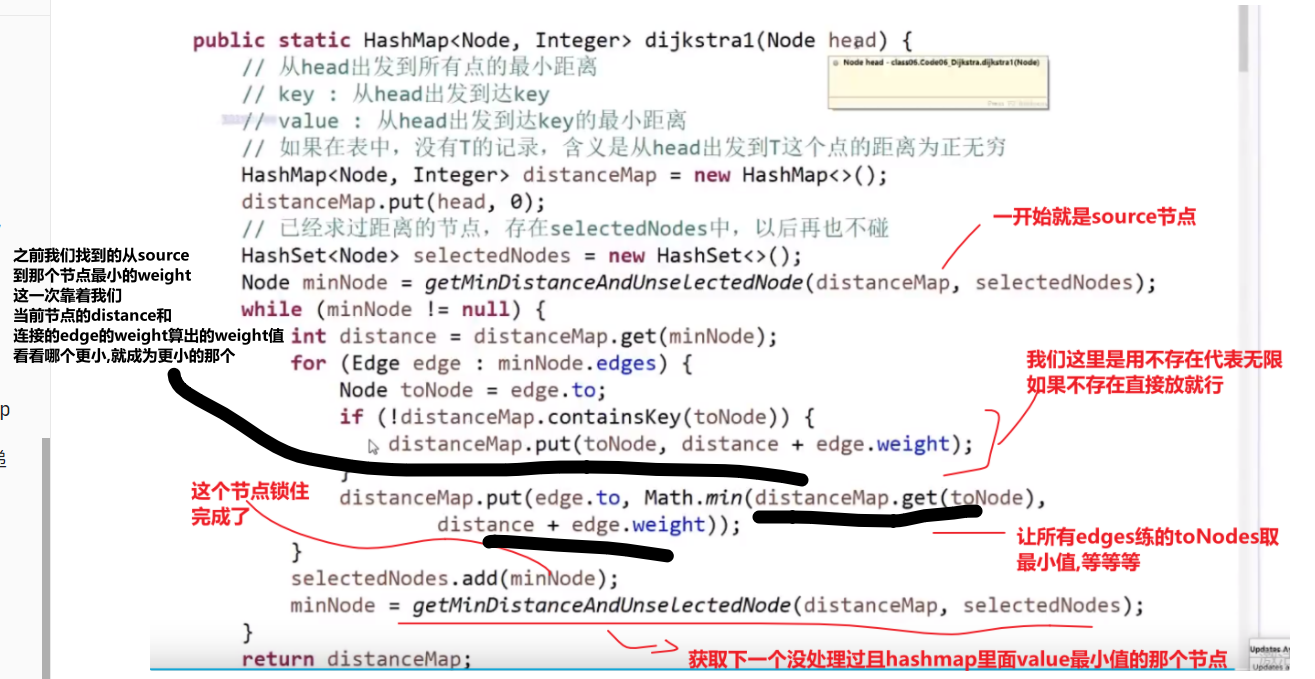
- 一开始存答案的 hashmap, 每个 key 对应一个图中的节点然后 value 就是 source 到那个节点的最小 weight, 一开始 source 到自己是 0 其他都是无限
- 先从 source 出发,然后找到他所有的 edges
- 然后把当前自己的 hashmap 中的值加上每个 edge 的 weight 值然后跟那个 edge 连向的节点当前数组中 hashmap 中的值比较,然后把 hashmap 值改成最小的那个值
- 处理完这个所有 edges, 我们就相当于结束了由 source 开始的所有 edges (我们也可以锁定当前节点在 hashmap 中的值,因为是第一次所以我们这次锁定就是 source 自己再 hashmap 中的值也就是 0, 他的距离到他自己就是 0)
- 然后我们从 hashmap 中选出除了以及当过当前节点的比如说 source 的所拥有的最小值的那个节点,然后让那个节点进行一样的操作 (看 edges 然后对于所有的 edges 的 toNodes 让他们的更新), 然后之后我们就把当前的这个节点在 hashmap 中的值锁死,然后让下一个…so on…
- 直到所有的都锁死了就结束,此时 hashmap 中存的值就是从 source 开始到图中每一个节点所需要的最小 weight (如果没有路就是无限)
一个优化 -> 在选择我们没有处理过且值最小的节点的时候是遍历的方式,可以使用堆结构来存储,然后每次就是存还没处理的,最小值的在堆顶,然后处理过的让他别参加堆结构
但是有一个问题,因为我们那些 values 是存从 source 到每个节点最小的 weight, 所以可能哪次遍历中我们会把一个堆结构中一个节点的值改了改成了一个更小的值,我们知道系统提供的堆结构无法接收让我们改变里面已经在的节点 (你要是硬改,系统里面自己做出的操作其实就跟我们直接遍历的复杂度都差不多了 —> 他需要全局扫描), 所以要是想实现,必须我们自己写一个堆
# 贪心算法
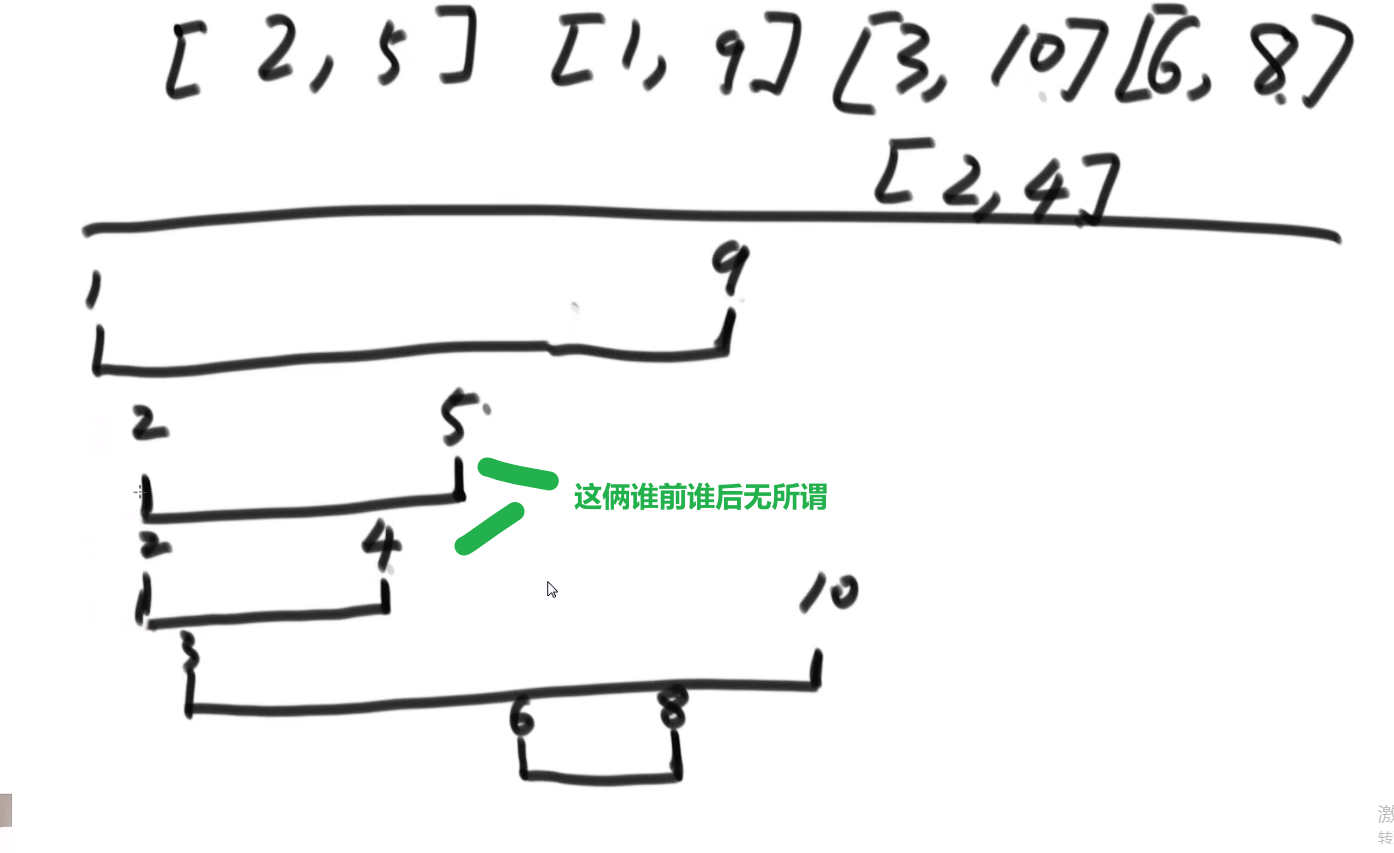
# 会议问题
- 开始时间最早的先安排是不对的,因为这个开始早的很长,之后要是有很多个短的项目都排不上

- 时间间隔最短的项目先安排也是不对的,万一你有两个长的在两遍不相互干扰,但是你有个短的正好一部分用了前面的时间另外一部分用了后面的时间

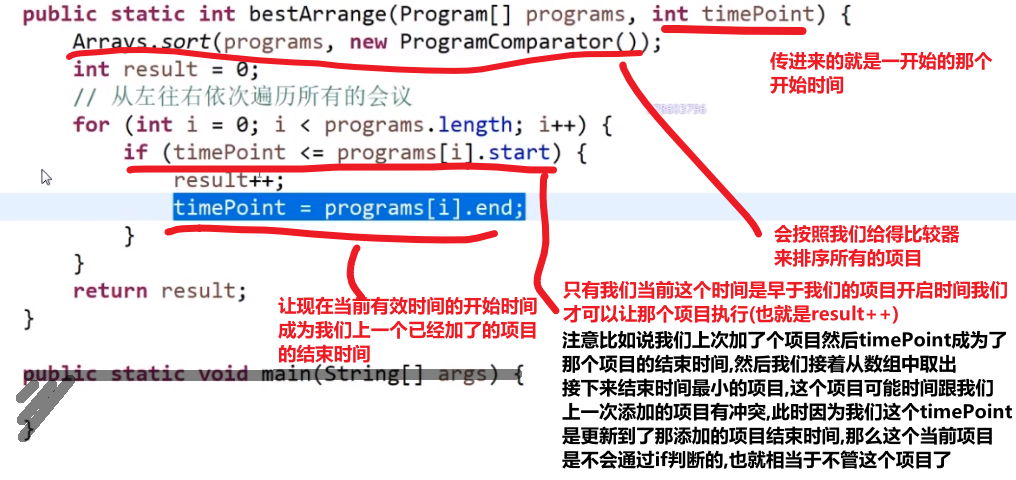
我们在这里正确的贪心的就是
哪一个项目的结束时间早,就先安排谁
- 把当前所有项目哪个结束的最早先安排
- 然后把所有因为我们安排了那个项目导致进行不了的项目删除掉
- 接着把下一个结束最早的项目进行安排
等等等…


# 贪心题目笔试中套路
多去想,如果想好一个贪心策略,尝试想出一个反例,想出一个就直接 pass 那个贪心策略,继续想别的贪心策略
# 字典序例子
而且注意,贪心策略需要注意传递性,像 1<2,2<3 这种都是默认的传递性,而有的传递性就不一样了,需要想好贪心策略
这里的传递性 (transitivity):

然后各种证明…
# 金条 (贪心) 问题–> 哈夫曼编码树
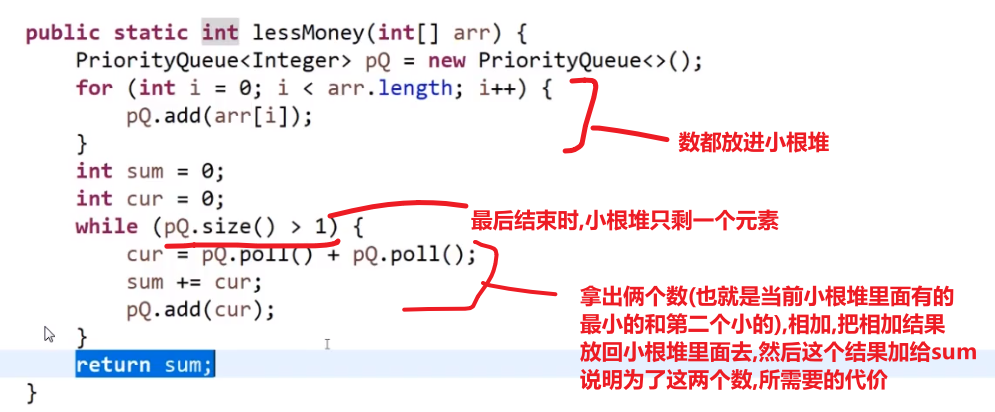
- 先把数都放进小根堆
- 接着取出最小的然后 (取完之后那个小根堆结构又形成) 再取那个时候最小的
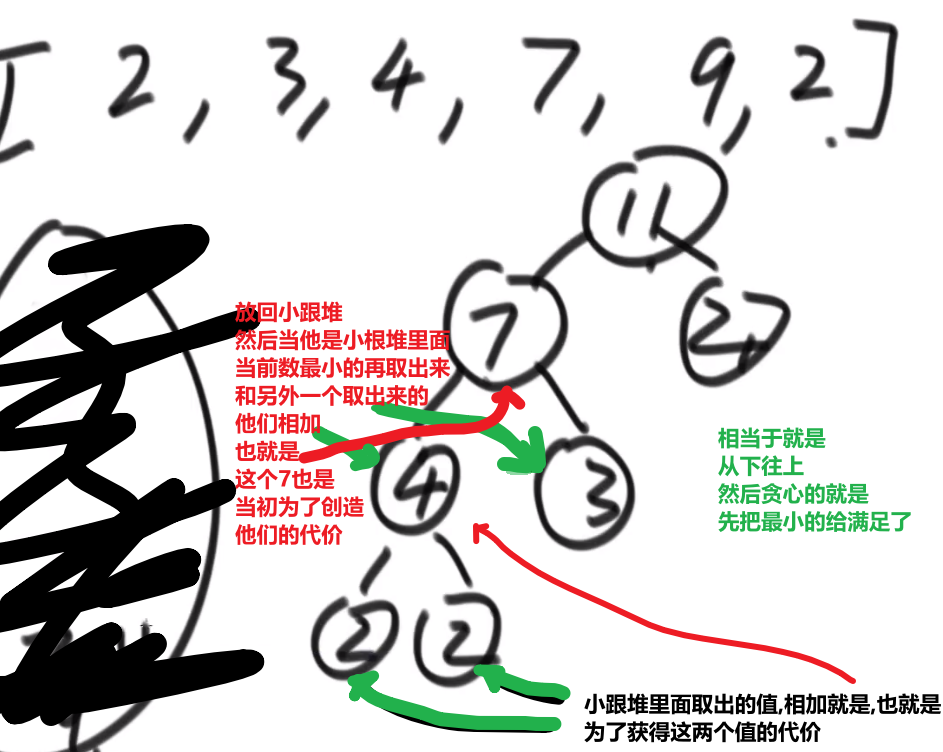
- 然后我们拿着这俩相加,也就是当初那个树里面分割自己形成的这两个数,然后那个被分割代表的那个就是所要出的代价 (看下面图,有点难说)
- 把这个相加的结果记录到一共的代价里面,然后再把这个相加的结果放回小根堆因为为了形成他,当初可能分割了他和另外一个的数的和
- 重复直到最后只剩一个数,那个数肯定是 60 (in this case), 就一开始的长度
这图只是过程中的一步,11 并不是一开始的长度,27 才是,后面的几步这里没画出来,可以看出来大概就是这么的步骤
最后树的真正样子应该是

贪心策略中
- 堆和排序是最常用的两个技巧
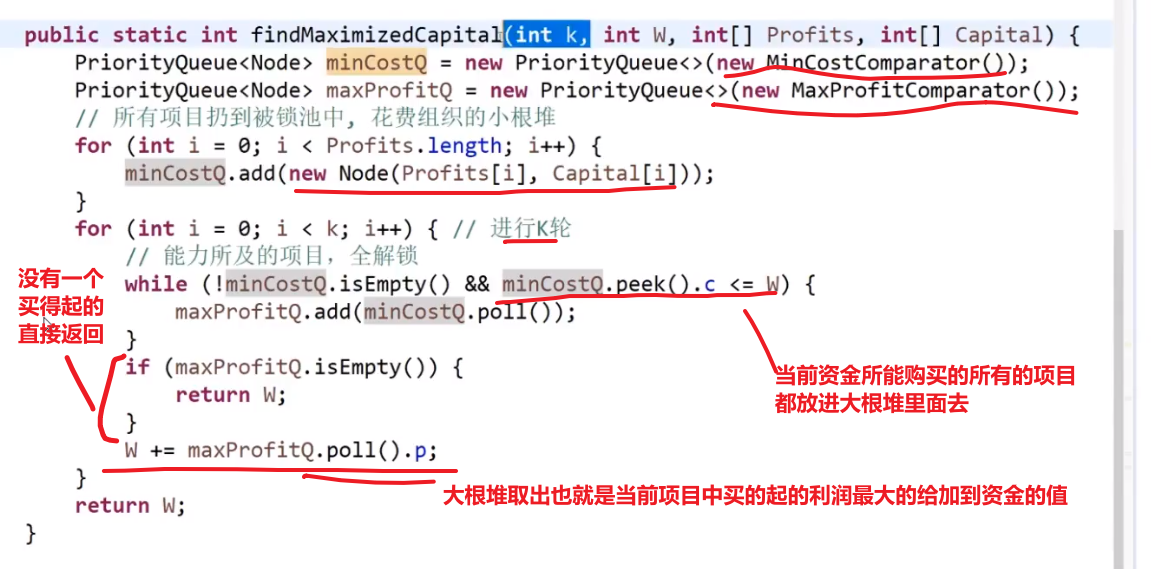
# 项目利润


想法是:
-
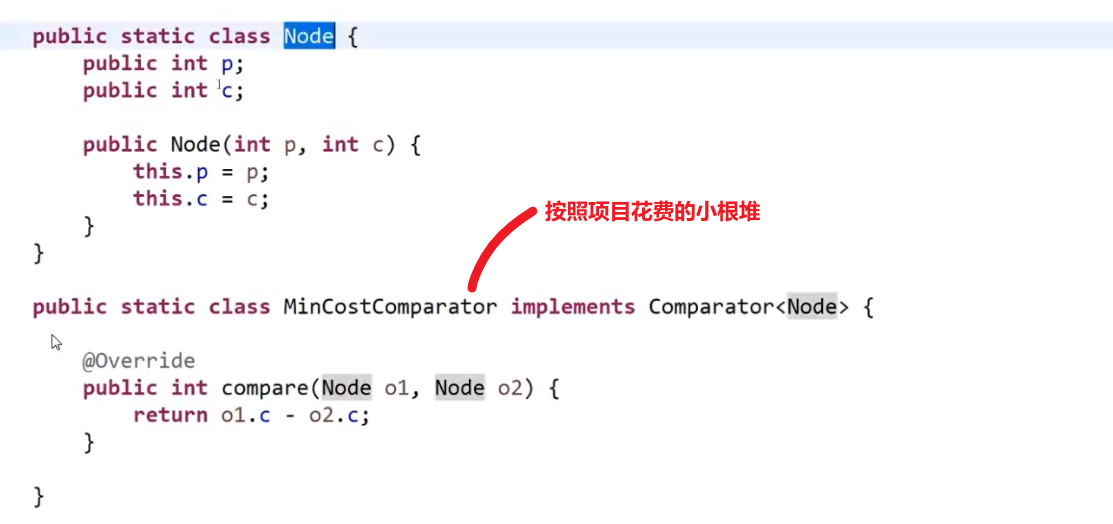
先把所有的项目按照他们的花费放到小根堆里面去 (自己写比较器)
-
再从小根堆取出当前资金可以花费的所有的项目
-
把那些项目放到一个按照项目利润的大根堆 (自己写比较器)
-
每次花费一个项目获得其利润都要更新当前资金值
-
如果遇到当前资金买不了任何小根堆里面的花费的 (从最低开始比) 也就代表大根堆里面没有元素了,或者已经交易了 k 次,那就直接返回当前资金
此处的贪心就是按照当前自己的资金可以买的所有的项目中挑选出利润最大的做,做完了更新资金,接着看当前资金可以买的所有的项目中挑选出利润最大的做,…
记住这种大根堆小根堆配合的!!!
这里是有两个可以排序的规则
- 花费
- 利润
然后就想一想对于每一个是用大根堆还是小根堆
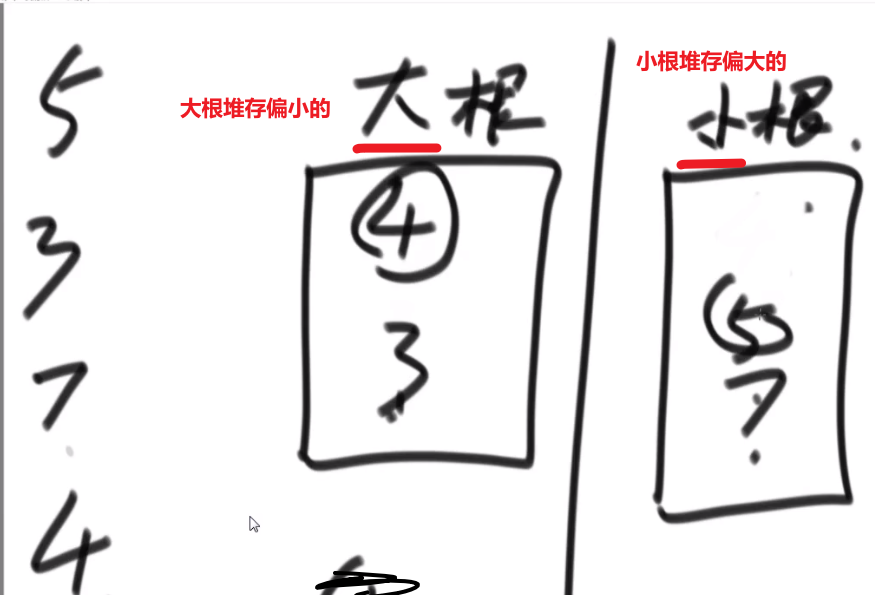
# 取得中位数
就是一个一个给你数,你如何很快地返回一个当前数中的中位数?
答案:大根堆和小根堆!
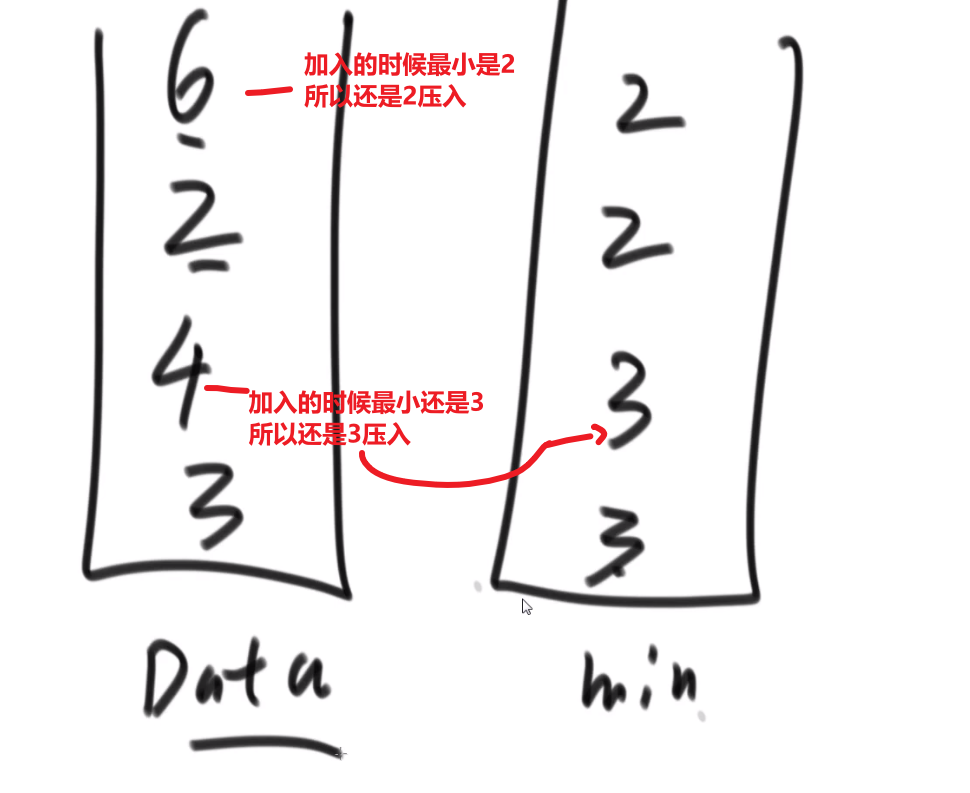
- 传进来一个数,我们先和大根堆堆顶比
- 如果这个数更小,我们直接放到大根堆里面
- 如果这个数更大,我们直接放到小根堆里面
- 然后接着就是检查当前大根堆和小根堆的 size 是不是大于等于 2
- 是的话就需要把 size 更大的那个根堆的元素取出来放到另外一个根堆里面去
- 不是的话就不用做什么
- 接着要还传了数,就接着处理
这样不管传了多少个数,较小的数都在大根堆里面,较大的数都在小根堆里面
因为各自维持了堆顶,中位数就很好获取到
然后就是看偶数还是奇数,偶数就是两个堆顶相加除 2, 奇数个就是 size 大的那个根堆的堆顶
很快,以为大根堆小根堆的调整水平都是 logN 水平的
# 暴力递归
回溯就是在递归的基础之上在每一个步骤上进行标记和取消标记的处理
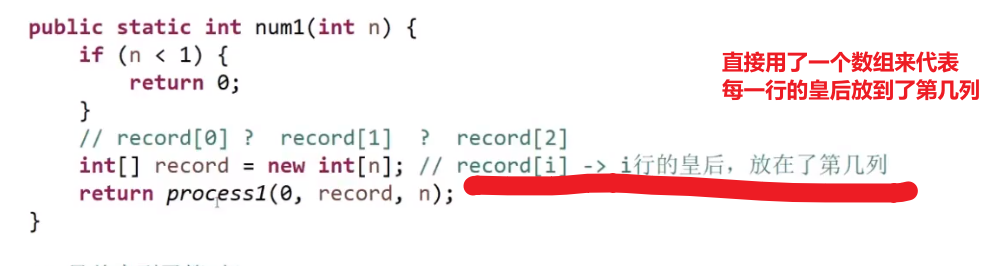
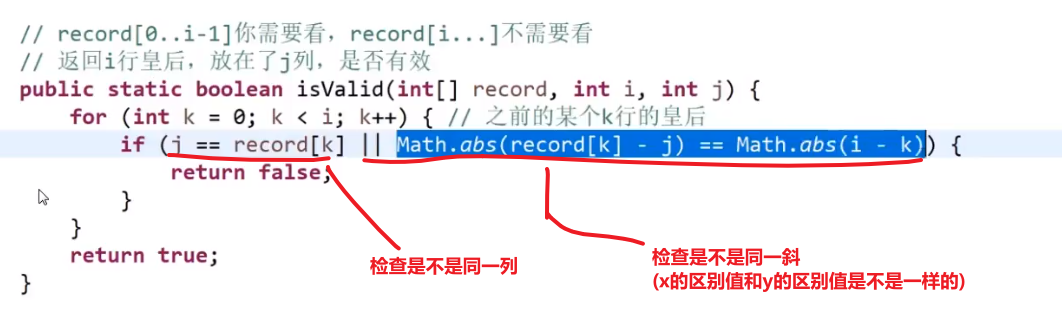
# N 皇后
此处的 for 循环检查每一列很关键,这可以直接给出所有可能性,这个性质其实就是 dfs, 每一条路都试了试
斜线就是 dy/dx=1, 也就是 change in x = change in y
这个算法 ** 时间复杂度是 NN** 因为第一行 N 种选择,第二行 N 种选择,第 N 行 N 种选择 —>(NxNxNxNx…) 相乘 N 次
这个复杂度优化不了,但是我们可以做些常数优化:
用位运算加速!
… 比较复杂
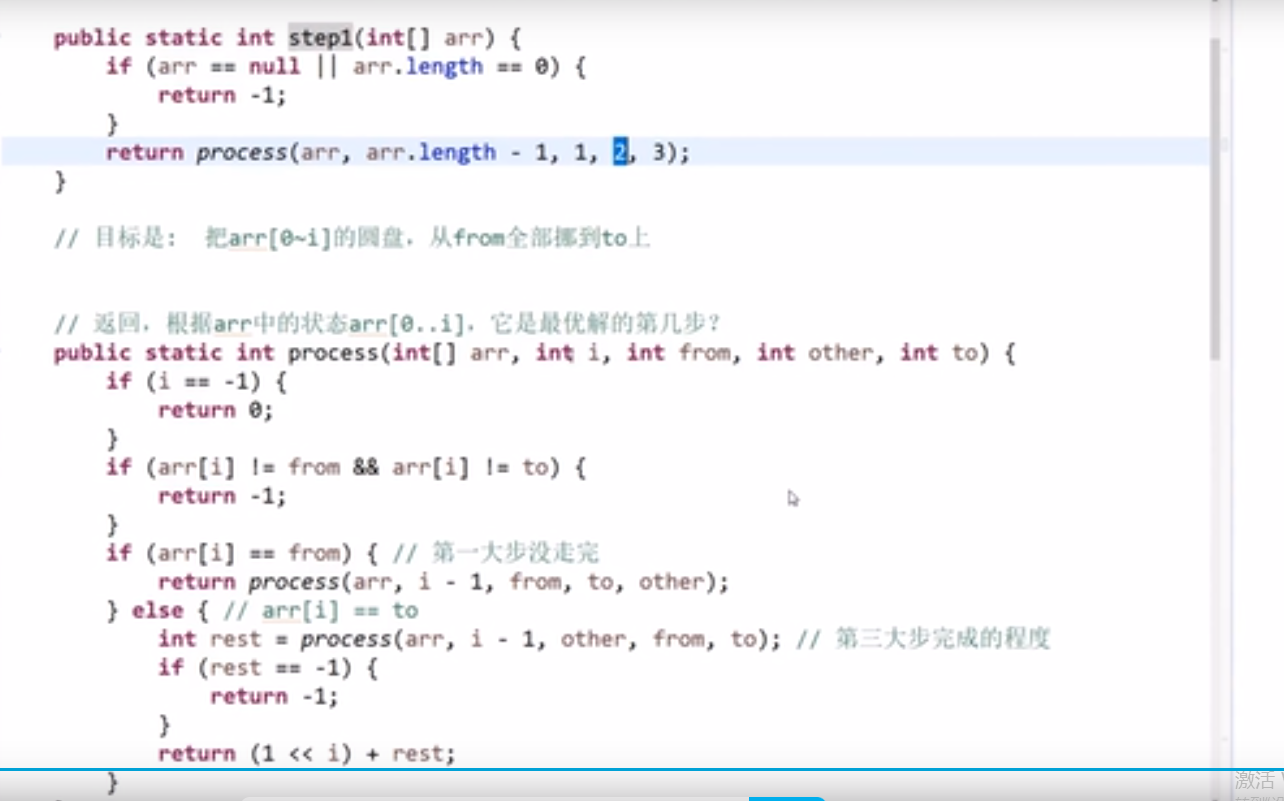
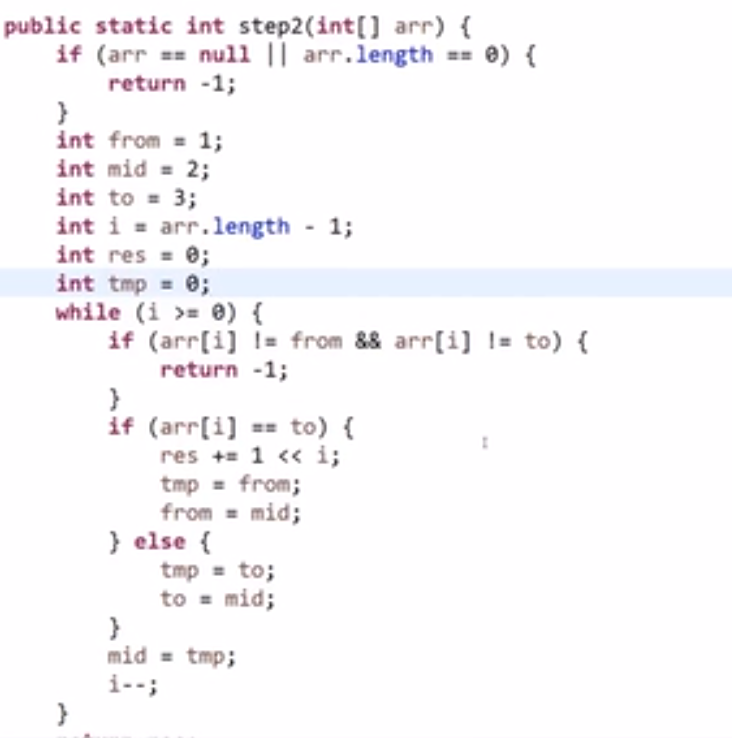
# 汉诺塔问题
解题思路:from: 圆盘所在位置;to: 圆盘要去的地方;help: 用于辅助
- n-1 个圆盘从 from 到 help; (也就是左 -> 中,此时 help 就是右)
- 第 n 个圆盘从 from 到 to; (也就是左 -> 右,此时 help 就是中)
- 把那 n-1 个圆盘从 help 移动到 to 上面来。 (也就是中 -> 右,此时 help 就是左)
# 打印一个字符串的全部子序列 (subsets),包括空字符串
- 区分子串和子序列: 给定 “pwwkew”
- 子串是 pww,wwk 等很多个子串 是连在一起的
- 子序列是 pwk,pke 等很多个子序列 ,但是子序列中的字符在字符串中不一定是连在一起的。
public class Code_03_PrintSubString {
public static void printSubStr(char[] chs,int i,String res){
if(i == chs.length){
System.out.println(res);
return;
}
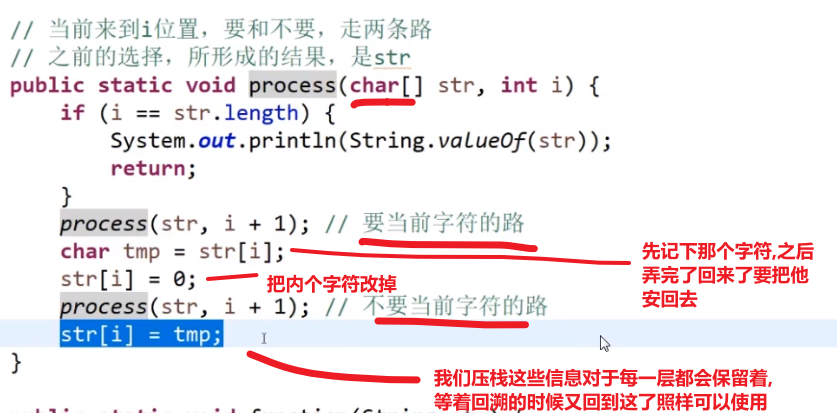
printSubStr(chs,i + 1,res);//不需要当前的字符的
printSubStr(chs,i + 1,res + chs[i]);//需要当前的字符的
}
public static void main(String[] args) {
String s = "abc";
printSubStr(s.toCharArray(),0,"");
}
}
//输出
(包含一个空字符串)
c
b
bc
a
ac
ab
abc老师做法:
# 打印一个字符串的全部子序列,要求不要出现重复字面值的子序列
输出前,加入 set 去重
# 打印一个字符串的全部排列
举个栗子:
字符不重复的情况下:
输入:abc
输出:abc acb bac bca cab cba
字符重复的情况下:
输入:acc
输出:acc acc cac cca cca cac
解题思路:把一个字符串看成由两部分组成:第一部分是它的第一个字符;第二部分是后面的所有字符。而我们求整个字符串的排列,可以看成两步。
求所有可能出现在第一个位置的字符,即把第一个字符和后面所有的字符交换。
固定第一个字符,求后面所有字符的排列。
这时候我们仍把后面的所有字符分成两个部分:后面字符的第一个字符,以及这个字符之后的所有字符。然后把第一个字符和它后面的所有字符交换。(重复 1、2 步骤)
printAllPermutations2 为分治限界方法,可以减少递归次数
public class Code_04_Print_All_Permutations {
public static void printAllPermutations1(String str) {
char[] chs = str.toCharArray();
process1(chs, 0);
}
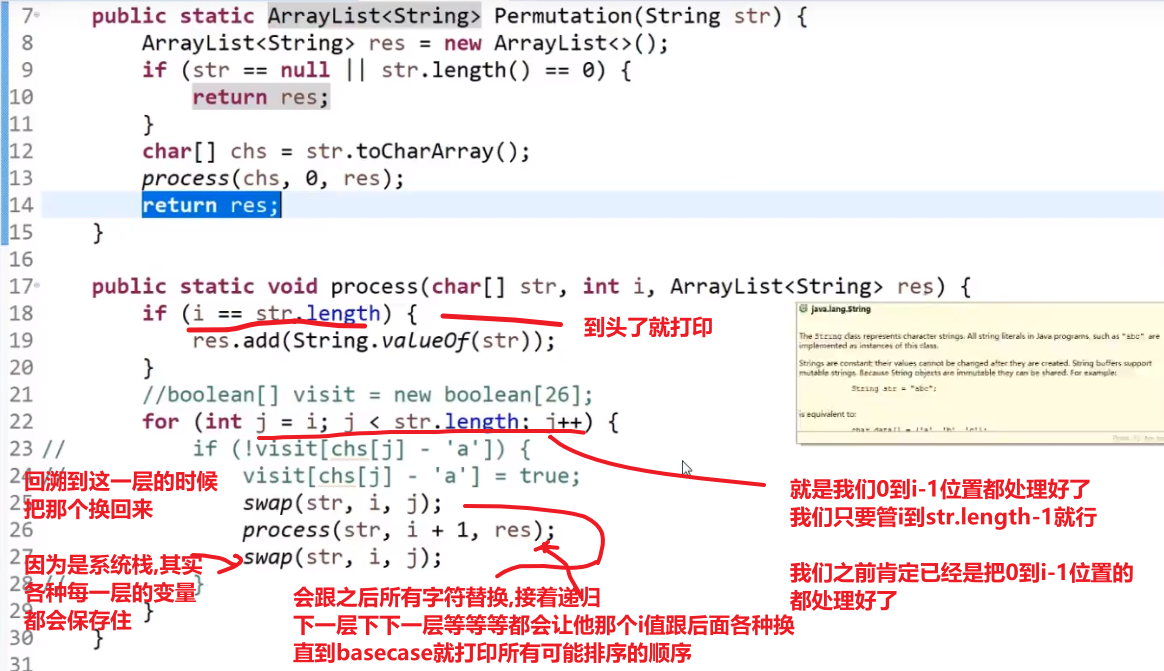
public static void process1(char[] chs, int i) {//交换的是当前位置之后的元素
if (i == chs.length) {
System.out.println(String.valueOf(chs));
}
//如果i没有终止,i... 都可以来到位置
for (int j = i; j < chs.length; j++) {//这个的理解是难点
swap(chs, i, j);
process1(chs, i + 1);
swap(chs, i, j);
}
}
// 在选择位置时就利用set ,减少递归次数,时间换空间
public static void printAllPermutations2(String str) {
char[] chs = str.toCharArray();
process2(chs, 0);
}
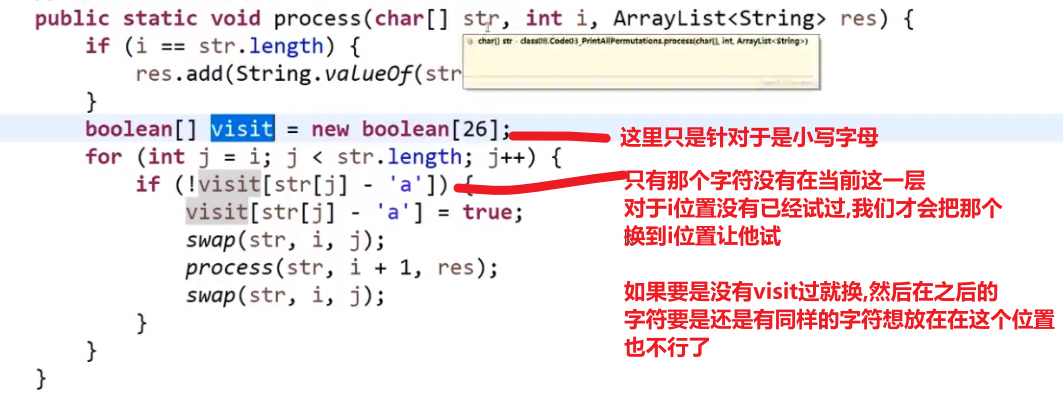
public static void process2(char[] chs, int i) {
if (i == chs.length) {
System.out.println(String.valueOf(chs));
}
HashSet<Character> set = new HashSet<>();
for (int j = i; j < chs.length; j++) {
if (!set.contains(chs[j])) {
set.add(chs[j]);
swap(chs, i, j);
process2(chs, i + 1);
swap(chs, i, j);
}
}
}
public static void swap(char[] chs, int i, int j) {
char tmp = chs[i];
chs[i] = chs[j];
chs[j] = tmp;
}
public static void main(String[] args) {
String test1 = "abc";
printAllPermutations1(test1);
System.out.println("======");
printAllPermutations2(test1);
System.out.println("======");
String test2 = "acc";
printAllPermutations1(test2);
System.out.println("======");
printAllPermutations2(test1);
System.out.println("======");
}
}
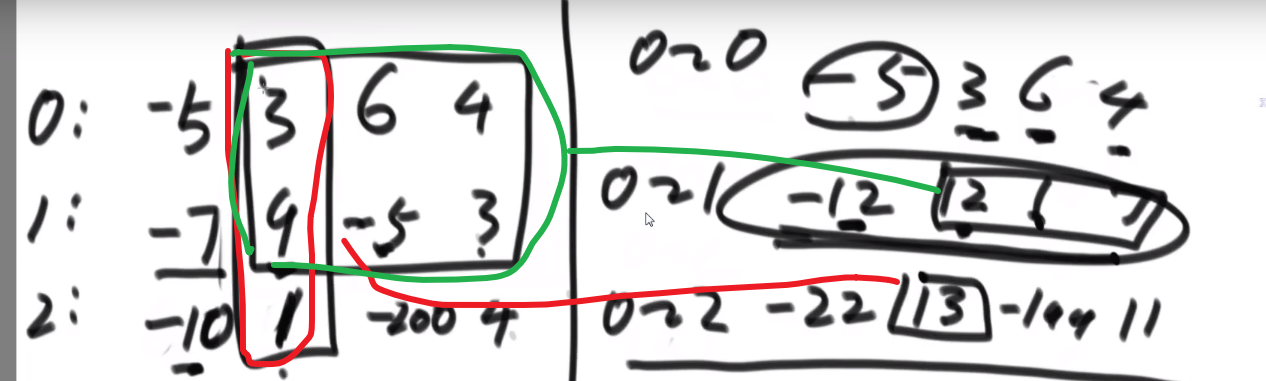
[[1,2,3],
[4,5,6],
[7,8,9]
]老师做法:
- 那个 str 的 char array 相当于就是我们递归的每一层所做的选择

个人认为那个 for 循环才是秒
- 首先一般你要考虑各种可能性 (然后这个可能性是指这第一个元素各种可能性,第二个元素也是各种可能性,so on…), 那么就可以考虑 for 循环第一个给他安排各种选择,然后递归调用自己的 (也就是对于他第二个元素等等), 然后那一层接着会调用下一层
- 这样就做到了每一层接着都实现了各种可能性,当然要保证 base case 到达了之后我们做出我们对于每种可能性的结果做出合理的处理 (存起来?打印?返回上一层?等等等)
- 我们还可以设置各种条件,比如说当前元素有没有已经存在等等等 (这个操作可能需要我们额外传一些参数,这样每一层都能知道当前状况) 如果有,也不要继续递归直接返回什么的,相当于把这个 branch 直接断掉了
# 打印一个字符串的全部排列,要求不要出现重复的排列
-
举个栗子:
输入:acc
输出:acc cac cca
思路同上,加入了 HashSet 来去重。
public class PrintAllSort {
public static void printAllSort(String string){
if(string == null){
return;
}
char[] chars = string.toCharArray();
if(chars.length > 0){
func2(0, chars);
}
}
// 对i及i以后的字符进行全排序
public static void func2(int i, char[] chars){
if(i == chars.length){
System.out.println(String.valueOf(chars));
}
// 用于保证每次交换的字符不存在重复字符
HashSet<Character> set = new HashSet<>();
for(int j = i; j < chars.length; j++){
// 只有之前没有交换过这个字符才会交换
if(!set.contains(chars[j])) {
set.add(chars[j]);
swap(i, j, chars); // 第i个位置有i~n-1这些选择
func2(i + 1, chars); // 搞第i+1的位置
swap(i, j, chars);
}
}
}
public static void swap(int i, int j, char[] chars){
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
}
// 测试
public static void main(String[] args) {
printAllSort("acc");
}
}老师做法:
这种方式比拿到所有数据然后去重要快,因为这里直接如果不达标,那整条路都不用走 **(把不可能的路直接杀死)**, 就不需要拿到所有数据–> 这里就是分支限界–> 时间复杂度并没有减少,因为要是这个条件根本没有复合的那还不一样都是所有的 (branches) 数据,只是常数项有优化罢了
# 纸牌
# 逆序栈
# 数字与字符串对应
还是从左到右试, 从左到右试时很经典的方法!
我们要这么想 (即使是假设)
- 首先就想 0 到 i-1 位置的元素都已经处理好了
- 我们只关心 i 到 nums.length-1 就行
如果我们这个当前 i 位置的是
- 0 的话,0 没有任何对应的,所以应该是跟之前的已经定好的搁一块决定的,我们直接返回 0
0 字符的话后面怎么转都没有效,因为我们没有 0 对应的字符也没有 0 开头的数字对应的字符

- 不是 0 的话
- 我们可以让那个元素直接变成对应的字符,然后处理 i+1 到 nums.length-1 就行
- 我们也可以看这个字符是 1,2 还是 3-9
- 如果是 3-9, 我们不可以让他跟 i+1 位置的字符结合,因为我们不能有 3 (以及) 开头的数字,(最高也只是 26 个字符,按照题目), 所以我们只能让他自己这个数字直接换,不要想什么跟 i-1 的位置结合,i-1 的位置是定的!对于我们当前层来说,i-1 那层他自己 (只要我们递归的逻辑做对) 自然会按照我们的逻辑试出他所可以的可能性的
- 如果是 1, 我们总可以让他跟 i+1 位置的数字结合,然后只处理 i+2 以及以后的 (因为开头是 1 的话,个位数任何树都可以有对应的字符)
- 如果是 2, 我们就可以看他跟 i+1 位置的数字结合有没有超过 26, 超过了我们就不可以,没超过我们就可以结合,然后只处理 i+2 以及以后的
# 物体重量和价值
思想就是,我们暴力递归
- 取不加当前重量和加当前重量的最大值
- 如果不加当前重量,就接着取不加下一个重量和加的重量的最大值
- 如果加当前重量,就接着取不加下一个重量和加的重量的最大值
- 反正我们 return 那里有 Math.max 确保我们每一层返回的都是最大可能性,然后这个是暴力递归 (除了一开始的 if statement 检测当前有没有已经超过了重量,相当于是分支限界) 确保了我们考虑到了每一个合法的可能性然后把最大的一层一层的返回出去了.
暴力递归尽量选
- 可变的参数为少的
- 可变的参数形式最简单 (一个值,不要链表什么的,除非必须要)
# 哈希函数
- 输入可以是无穷大,输出是有限范围内
- 同样的输入,同样的输出
- 不同输入可能会有同样的输出–> 毕竟无限输入然后输出是有限的
- 均匀的,离散的,分散在哈希表

如果想要一张哈希表存大量的数据,放到内存里面,那么如果数据不一样的话,哈希表占用很大的,我们希望数据是有很多是重的,这样多个只不过是对于那个重复的元素的 value 改变改的更大而不是不同数据的那样让很多位置都占满
- 这样我们可以把那些一堆数据 apply 哈希函数,让他们均匀的分散的在哈希表
- 然后再对哈希函数取模 (比如说 100), 再把对应数据存到对应取模后的位置
- 那么这样我们最多也就是 0-99 个 key, 而且因为哈希函数保证能差不多均匀的分散来–> 相当于是把数据都分散到 100 个文件上 (存到硬盘)
- 那么我们取模后所有数据也都是均匀的分散开来
- 而我们需要某一个数据处理的时候,我们只需要获取一个 key 对应的值,然后只对那个放内存做处理,这样就做到了不用整张表一大堆 key 都放到内存,可能会让内存爆掉如果内存空间不足
- 我们哈希表每一个对应的下标位置可以存的也是哈希表,只不过这个是更小数据,内存不会爆
- 如果想要处理多个下标的数据,我们可以一个一个来,先把第一个放到内存里面处理,接着第二个,… 所以内存是不会爆的
如果有一个下标的链表长度超过一个数 (说明其他也都差不多,均匀分散开来), 那么就会扩容
比如说直接扩容成两倍,那么每一个数就接着哈希函数均匀的分散在新的扩容后的哈希表里
- 就比如说想找一个东西,那么会先哈希值 (O (1)), 然后模一个值 (O (1))
- 找到了下标就会去那个下表的链表找,如果链表长度为 k, 那么就会是 O (k)
- 如果链表不是特边长,那么查删改一个数据都是 O (1), 因为 k 接近于常数
扩容代价:
- 如果加了 n 个数据,就会最多最多 (也就是每次翻倍都会扩容) 经历 log (n) 次扩容,实际扩容次数远远少于 log (n) 不过只是常数减少,还是这个级别
- 每次扩容都需要 O (n) 的代价 (重新算哈希值,取模,然后挨个放到对应的位置去)
- 总扩容代价就是 O (NlogN), 这是对于加了 n 个数据的扩容的代价
我们除以 n 就可以得出, 单次查询,删除,更改一个数据的平均代价就是 O (logn) 的级别
这个 O (logn) 会是小常数,如果链表不要太长
java 虚拟机可以帮助我们做哈希离线技术
就是我们一个哈希表做扩容不占用用户用哈希表的在线时间的
实际上哈希表用起来无比接近于 O (1)
但是理论就是 O (logn)
# 设计一个数据结构
- 两个 map
- 一个是数据 key,index 作为 value
- 一个是数据 value,index 作为 key
- 一个记录 size, 一开始是 0
我们只需要随机生产 0-size-1 的值,就可以等概率获得一个数字,然后用 map 取就行了
对于删除操作,我们可以先通过那个 key 在 map 里面找到对应的 index, 然后更新那个 index 到那个被删除的数据的 index, 然后更新 size
使用一个或多个哈希表,可以做到很多操作变成 O (1) 操作!实际上来说 (虽然哈希表是 log (N) 的操作,但是之前提到的技术可以做到实际就是 O (1) 的)
# 岛问题和并查集
# 岛问题
- 遍历如果遇到一个 1, 就把当前位置给到一个 infect 函数
- 这个函数就会把这个位置以及周围是 1 的全部变成 2
- 此时我们就可以让 ans++, 说明找到一个岛
- 然后我们继续遍历,如果遇到是 2 就继续找,只有是 1 的时候我们才把当前位置传给 infect
- so on…
这整个的时间复杂度是 O (n*m),n 代表 number of rows, m 代表 number of columns (就是主函数里面那个 nested for loop)
外面那个 nested for loop 会碰每一个元素一次
虽然 infect 是递归但其实并不高,每一个位置的元素只能被他的上下左右触及到,所以每一个位置的元素在 infect 阶段最多最多调用四次,所以整个 infect 每个元素都是被调用有限几次。不要想一个位置调用谁,而是想一个位置被谁调用了
那个还是外面那个 nested for loop 最耗时间
并行算法解决这个问题:
注意 acm, 面试,一般都是单 cpu, 单进程的题目
但是也有可能是并行触发的题目–> 并发集
# 并查集
一个支持集合合并非常快速的结构
有两个操作:
- 检查两个集合是不是同一个集合
- 把两个集合变成一个集合
用我们经典的数据结构,无法做到两个操作都是 O (1), 反正至少一个得要比遍历
我们并查集就可以在 O (1) 时间复杂度实现这两个操作
并查集的重要思想在于,用集合中的一个元素代表集合。我曾看过一个有趣的比喻,把集合比喻成帮派,而代表元素则是帮主。接下来我们利用这个比喻,看看并查集是如何运作的。
最开始,所有大侠各自为战。他们各自的帮主自然就是自己。(对于只有一个元素的集合,代表元素自然是唯一的那个元素)
现在 1 号和 3 号比武,假设 1 号赢了(这里具体谁赢暂时不重要),那么 3 号就认 1 号作帮主 *(合并 1 号和 3 号所在的集合,1 号为代表元素)*。
现在 2 号想和 3 号比武 *(合并 3 号和 2 号所在的集合),但 3 号表示,别跟我打,让我帮主来收拾你(合并代表元素)*。不妨设这次又是 1 号赢了,那么 2 号也认 1 号做帮主。
现在我们假设 4、5、6 号也进行了一番帮派合并,江湖局势变成下面这样:
现在假设 2 号想与 6 号比,跟刚刚说的一样,喊帮主 1 号和 4 号出来打一架(帮主真辛苦啊)。1 号胜利后,4 号认 1 号为帮主,当然他的手下也都是跟着投降了。
好了,比喻结束了。如果你有一点图论基础,相信你已经觉察到,这是一个树状的结构,要寻找集合的代表元素,只需要一层一层往上访问父节点(图中箭头所指的圆),直达树的根节点(图中橙色的圆)即可。根节点的父节点是它自己。我们可以直接把它画成一棵树:
# 路径压缩
最简单的并查集效率是比较低的。例如,来看下面这个场景:
现在我们要 merge (2,3),于是从 2 找到 1,fa [1]=3,于是变成了这样:
然后我们又找来一个元素 4,并需要执行 merge (2,4):
从 2 找到 1,再找到 3,然后 fa [3]=4,于是变成了这样:
大家应该有感觉了,这样可能会形成一条长长的链,随着链越来越长,我们想要从底部找到根节点会变得越来越难。
怎么解决呢?我们可以使用路径压缩的方法。既然我们只关心一个元素对应的根节点,那我们希望每个元素到根节点的路径尽可能短,最好只需要一步,像这样:
其实这说来也很好实现。只要我们在查询的过程中,把沿途的每个节点的父节点都设为根节点即可。下一次再查询时,我们就可以省很多事。
这个就代表我们那个圈,就是不管什么类型进来我们就先让变成一个集合 (像是), 相当于给他包装一层就是这个 element 类
并查集使用的前提就是初始化的时候把所有数据给我们了,这样我们才可以挨个包装成 Element 然后你接着可以做检查是不是同一集合,以及把两个不是同一个集合的合并成一个集合这种操作。注意这里面数据只是针对于你一开始初始化的,不能使用别的数据
所以我们只需要调用并查集的构造函数把所有数据传进去
之后我们就可以对这些数据调用 isSameSet 和 Union 方法,然后时间复杂度很低 O (1)
尽管这两个方法都调用了 findHead 方法, 其实只要方法被调用够多次数 (O (n) 次)(他内部那个扁平化优化), 其实调用他的时间复杂度是非常非常接近于 O (1)—>(他的证明很难很难,花了 20 多年才证明出来)
# 使用并查集解决岛问题
比如说岛问题给的二维数组特别特别大,那么我们之前那种方法只用一个 CPU 就会非常非常耗时间
首先,使用两个 CPU:
其实我们整个来看就一个岛,但是
- 处理左边的 CPU 找到两个岛
- 处理右边的 CPU 也会找到两个岛
这是不对的,所以我们两个 CPU 需要想一个合并逻辑去求出一个正确的岛的数量
我们合并逻辑
- 首先记录我们从哪个点开始感染每一块岛
- 对于每个感染到的在边缘 (分割的边缘), 我们给他们做个记号 (记号就是我们开始感染的那个点)
比如说处理我们左边的 CPU 的数据
右边同理:
做合并:
一开始有多少 (从哪开始的) 感染点–> 四个,ABCD, 所以相当于传进去给并查集的构造函数形成四个集合
然后左边右边 CPU 分割算出 2 个岛,也就是一共 4 个岛
- 我们对于 (分割的) 边缘那块连在一起的集合 (如果他们不是同一个集合) 让他们连在一起,然后让总共岛数 - 1
此时集合是 {A,C} {B}
- 接着看,此时 B 所在的岛和 C 所在的岛 **(他们代表的集合不是同一个,而且还在边缘除相连接,所以就合并!)** 合并在一起,总数 - 1
此时集合是 {A,C,B}
- 同理 B 和 D 代表的集合不是同一个,而且还在边缘除相连接,所以就合并,总数 - 1
此时集合是
- 然后 A 和 D 检查,现在是一同一个集合了!!!所以不用 - 1 (而且因为之后也没有其他集合要检查了,如果有的话就继续看然后合并等等等), 也就是现在岛数就是 1, 也就是正确答案
这样就做到了两个 CPU 分别处理一半,然后最后合并等等操作还是正确答案,当然比一个 CPU 处理整块快
多个 CPU:
同理,分成好多块,然后让每一个 CPU 收集四边 (四边都要!) 的信息,然后就可以之后合并就跟四边都要合并一下,最后合并成一大块,速度当然非常快
# KMP
暴力解法的时间复杂度是 O (n*m)–>n 是 str1 的长度,m 是 str2 的长度
我们需要遍历 str1 然后每一个开头我们都可能要检查接下来的 m 字符看对不对,如果不对要接着 str1 下一个字符看 (不可以直接跳!) 接下来的 m 字符看对不对
KMP
不要取到整的是因为取到整到的话,自己当然跟自己一样,所以没有意义
所以 k 这个字符存什么信息?存对于他之前那些字符比较,最大的且一样前后缀的那个才是,这里就是 3
对于 **str2 (不是对于较长的 str1 求的!!)** 每一个字符,我们都需要这样的信息
注意对于
- 第一个字符,因为前面压根没有任何字符,我们直接就是 **-1**
- 第二个字符之前就一个字符,其实怎么样都会是 0
- 其他就正常的像我上面说的求
这个 next 数组,就代表我们知道 str2 这个字符串中,任何一个字符他前面的字符串最长的前缀和后缀的长度,我都知道
我们可以拿和这个 next 数组做到 KMP 加速,解决问题
列子:
- 如果是经典暴力做法:我们发现这个不一样,我们就会 str1 中 X 的位置回跳到 i+1 位置以及 str2 中 Y 的位置回跳到 0 位置,继续开始比
- 如果是 KMP 做法:当我们第一次发现 str1 和 str2 有一个字符不一样 (X 和 Y), 我们就知道 str2 中对于这个 Y 字符他前面的字符串最长的前缀和后缀的长度,比如说这一块 (他们当然可以相交,就是错过去,这里只是为了好看理解就放了那么两端的前缀和后缀):
我们让 str1 中不要回跳到 i+1 位置,还是待在 X 的位置
我们让 str2 中会跳到这个位置:

然后让当前 str2 中新的这个位置和 str1 的 X 的位置相比,看看是不是同一个字符
这个相当于是把前缀位置给推倒后缀相同的部分的位置上去

原来我们是检查 i 开头能不能配出 str2, 现在我们这么做了后,相当于是检查 j 开头的能不能配出 str2, 我们只让可能不同的位置往下验
这么做,我们就可以
- 不用让 str1 回到 i+1 位置 (也有可能回到,具体看 str2 的那个 next 数组), 而是像图里面一样直接让从 x 位置重新比,只不过这次要是找到了,那么返回的开始 index 是 j 而不是 i, 相当于此时是从 j 比的,但我们并没有真正从 j 然后 j+1,… 开始比的,而是直接跳过了直接比 x 因为我们知道 j,j+1,…,x-1 位置上的元素一定跟我们的 str2 的 u,u+1,…,y-1 位置的元素一样,我们才会比到 X 和 Y 位置,我们还知道 u,u+1,…,y-1 这一块,按照我们 Y 字符对应的 next 数组的下标的位置知道对应的前缀是哪一块,也就是 v,v+1,…,k-1, 所以 j,j+1,…,x-1==v,v+1,…,k-1, 这一块是两个 str 都一样的,我们接着只需要比较 str1 的 x 的位置和 str2 的 k 位置的元素是不是同一个就行了 **(前面我们已经确定是一样的了)**, 如果是同一个,那么如果 str1 如果还有元素,就会跟 str2 接下来的 (k+1,k+2,…) 的元素比,如果没有的话,那就不对了,我们这个 str2 当前还没比的元素明显还有,所以就返回没有找到。我们还知道 i 位置到 j-1 位置一定 (作为开头) 配不出 str2, 所以我们把检查位置直接挪到 j 位置.
- 我们也不需要让 str2 回到 0 (v) 位置继续比,我们直接回到 k 位置就行了,道理上面都说了
相当于两个字符串回去的程度都没暴力方式的那么多罢了,道理还是一样的,一个一个比等等等
具体例子:
暴力解法:发现最后那一个不一样,会接着从 i+1 也就是 b 开始比 (跟 str 的 0 位置也就是 a) 看看一不一样,发现第一个就不一样,接着就是 i+2…
KMP:
相当于我们把 str2 给往右挪了:

如果这么假设,那就代表:
可以看出,我们这里岂不是找出了一个对于 y 字符他当前 next 对应下标存的值还要大的值–> 就是比我们之前看 str2 算 next 数组,出现了更大的对于 y 字符前面的字符串来说前缀和后缀相等的情况–> 这不可能,因为我们 next 存的就是最大最大的对于 y 字符前面的字符串来说前缀和后缀相等的长度,所以我们的假设是不对的,证明 i 到 j-1 位置会有开头然后会匹配 str2 的情况是不可能发生的
所以我们可以直接从 i 位置跳到 j 位置,不用担心中间的字符会有开头然后会匹配 str2 的情况发生 (因为压根不会发生!)
时间复杂度:
这两个变量在我们的 while 循环里面,最大幅度就是 2N, 所以那个 while 循环时间复杂度就是 O (N)
找 next 数组:
-
第一个默认是 - 1
-
第二个默认是 0
-
之后每一个 i 位置都要靠前面的 i-1 位置的元素得出
-
对于 i 位置来说,如果 next 数组的 i-1 位置是 x, 那么你需要在 str2 里面的 x 位置的元素跟 i-1 位置的元素比较
- 如果一样,那么 next 数组中,i 位置的元素是 x+1
必须是 x+1, 可以反证如果不是的话,那么 next 数组中 i-1 位置的元素就不会是 x 了
-
如果不一样,比如说 next 数组中 x 位置存的是 y, 那么现在就去 str2 里面拿 y 位置的字符跟 i-1 位置字符比
- 如果一样,那么 next 数组中,i 位置的元素是 y+1
- 如果不一样,继续跳…
直到最后跳到 next 数组的 0 位置比较
-> 如果一样那么,i 位置的元素是 1
-> 如果不一样,就是 0
这个的时间复杂度:
跟之前 KMP 主方法一样的,都是线性的,也就是 O (M) 时间复杂度
整个复杂度:
我们知道获取 next 数组是 O (M) 的–>M 是 str2 的长度
我们知道 KMP 主方法是 O (N) 的–>N 是 str1 的长度
我们还知道 str1 是至少要比 str2 长的, 所以整个 KMP 算法就是 O (N).
# Manacher 算法
解决字符串最长的回文子串的问题,以及很多…
一般解法:
- 每个字符作为中心轴,像左右两边阔,看看是不是回文
但是这种方法,可能会因为长度为偶数,而错过某个回文,比如说:
解决方法,加一个 #到最前面和最后面,然后每两个字符之间加一个#
然后再对每一个字符做出这种操作,就可以获得每个字符左右的回文包括 #的,然后我们需要 / 2 就可以获得对于每一个字符正确的回文长度 (相当于除 2 是把所有 #给清掉了)
其实加的特殊字符是什么都行,就算是原本数组里面有这个字符也没事,不会影响最后答案的!
经典做法的时间复杂度就是 O (N2), 因为比如说:
不管是哪个元素都会扩到两边头,然后又有 n 个元素,所以就是 O (N2)
Manacher 也是差不多想法,但是做了加速,导致时间复杂度为 O (N)
- 首先有个 R 变量,一开始是 - 1, 在我们看每一个字符的回文的时候,记录当前最大的右边界的值

- 然后有个 C 变量,一开始是 - 1, 在我们看每一个字符的回文的时候,找到的就是对于那个字符找到的那个回文的中心位置,这个 C 也是只存最右的中心位置
…(看下方!)
# 原始问题
Manacher 算法是由题目 “求字符串中最长回文子串的长度” 而来。比如 abcdcb 的最长回文子串为 bcdcb,其长度为 5。
我们可以遍历字符串中的每个字符,当遍历到某个字符时就比较一下其左边相邻的字符和其右边相邻的字符是否相同,如果相同则继续比较其右边的右边和其左边的左边是否相同,如果相同则继续比较……,我们暂且称这个过程为向外 “扩”。当 “扩” 不动时,经过的所有字符组成的子串就是以当前遍历字符为中心的最长回文子串。
我们每次遍历都能得到一个最长回文子串的长度,使用一个全局变量保存最大的那个,遍历完后就能得到此题的解。但分析这种方法的时间复杂度:当来到第一个字符时,只能扩其本身即 1 个;来到第二个字符时,最多扩两个;……;来到字符串中间那个字符时,最多扩 (n-1)/2+1 个;因此时间复杂度为 1+2+……+(n-1)/2+1 即 O (N^2)。但 Manacher 算法却能做到 O (N)。
注意:在找回文的过程中,一般要在每个字符中间插入 #之类的间隔符,来避免奇数和偶数的差别回文
# 补充概念:
回文直径:以一个位置为中心,扩出来整个串的长度为回文直径
回文半径:以一个位置为中心,扩出来半个串长度为回文半径
回文数组:对于字符串而言,从 0 位置开始,一直到最后,新建一个数组,数组中保存对应位置的回文半径。
最右回文右边界:所有回文半径中,最靠右的边界,回文右边界只要没更新,记录最早取得此处的回文中心。
Manacher 在向外扩展的过程整体跟之前的算法相似,但是有加速。
# 【步骤】
-
回文右边界 R 不包含位置 i,此时暴力扩展,直到 R 包含 i。(就是当前位置是> R 当时的值,就是不包含,只能暴力扩展)
-
i 位置在回文有边界内时 (当前位置 <=R 当时的值),知道了回文右边界可以知道回文左边界,对称中心为 c,此时关于 c 做 i 的对称点 i‘
- 若 i‘的回文彻底在 c 为中心的回文里面,此时 i 的回文半径和 i’的回文半径相同 (所以全径也相同)
注意正常来讲中间都是加特殊字符的只是这里为了方便而没有那么做
- i 位置的对称位置 i’的回文半径越过了以 c 为中心的左边范围。(i‘扩出的范围以 c 为中心的回文没包住,存在一部分在回文直径外面)此时 i 的回文半径是 R-i (所以全径就是 2 (R-i) 长度)*
注意正常来讲中间都是加特殊字符的只是这里为了方便而没有那么做
- 正好 i‘的回文半径正好跟左边 L 相等,此时可以直到 i 的回文半径大于等于 R-i (其实 this case 就是 i’的半径),然后需要判断 R 后面的位置,重新返回第一步 (因为不确定 i 的回文有没有可能更远)。
注意正常来讲中间都是加特殊字符的只是这里为了方便而没有那么做
整个算法的复杂度 O (n),虽然第一步和第 2 步的第三点花费时间长,但是第一步和第 2 步的第三点都会扩展 R,依次变化的过程中,R 最多也就是变化到 n,所以时间复杂度为 O (n)
伪代码:
下方代码是为了:
- 让传进来的字符串或者字符数组变成那种包含特殊字符的字符数组 str
- 然后定义新的 int 数组用来装 str 的每一个字符的回文半径
- 定义 C,R 变量 (之前说过)
- 然后就是我们上面的说的,看在不在范围内,不在就暴力扩,在就看左边界有没有超过,有没有压着 L 等等等。让那个存 str 的每一个字符的回文半径的数组填满
- 期间注意更新 R 值和 C 值
# 实际代码
注意那个一开始获取对于 i 最小需要扩的位置的代码可以看视频 https://www.bilibili.com/video/BV13g41157hK?p=13, 第 1:26:30 部分,说的很清晰,基本上就是考虑了我们上面所说的所有情况然后取了最小的
这里的代码主要是为了短,想法跟我们上面所说的其实有些区别,不过主要想法是一样的,只不过没有像我们说的按照不同情况各种 if else 等等等
这里我们的那个 str 处理串的回文半径长度能帮我门解决很多问题,而找出一个字符或者字符数组的最长的回文子串 (的长度) 只是其中的一个问题
# 滑动窗口
有两个原则
- L 和 R 只能往右走
- L 不能比 R 还右
R++ 代表把一个元素加进窗口
L++ 代表把一个元素移出窗口
而上面那个题需要我们每次窗口更新都获取最大值,我们可以遍历这也可以,但是效率低,我们可以更新一下结构让用户快速获取最大值,效率会很快
-
首先有一个双向的队列 (也就是两端都可以取值), 这个队列用来存下标的 (为什么不存元素?因为存下标可以通过数组快速地获取到对应的值,存下标还可以给我们更多的信息)
-
我们这个双向的队列从头到尾要保证是每一次窗口的值由大变小的排他们的下标
-
当我们 R++, 尝试把这个新加的元素从队列尾部开始加
-
如果这个新加的元素值比我们的队列尾部那个元素要小,直接让这个新加的元素的下标加入到尾部
-
如果这个新加的元素值比我们的队列尾部那个元素要大或者等于,把那个尾部的元素弹出,然后比较下一个,一直比到为空或者遇到比新加的元素值大的元素,我们才让这个新加的元素的下标加入到尾部
这些被弹出的元素再也不可能成为此时以及以后的窗口的最大值了,因为我们这个新加的元素下标目前是最右的 (记得 L 和 R 只会往右走) 所以最晚过期,且新加的元素值又比那些值要大,那么肯定当前或者之后的窗口要是有这个元素肯定会比过我们当前弹出的元素 (等于或者小于这个新加的元素的值), 所以我们这些值其实不需要了,直接弹出就好了
此时我们的队列的头保留的就是我们每一次窗口的最大值
-
-
当我们 L++, 说明想要把一个元素移出我们当前这个窗口,我们检查这个移出元素的下标
- 如果这个下标跟我们当前双向队列的头位置存的下标一样,直接让头弹出
- 如果这个下标跟我们当前双向队列的头位置存的下标不一样, 不需要管
这个双向队列存的信息就是
"如果目前的窗口不再扩 (R 不 ++), 且我们选择让 L++ 也就是移出一个个元素,谁会依次成为最大值的这个优先级顺序的信息"
这个双向队列的总代价 (时间复杂度) 是 O (N), 因为你这个滑动窗口往右走的时候,走过 N 个元素,我们双向队列最多让 N 个元素弹出,最多让 N 个元素加入,所以代价就是 O (N) 级别,这个是对于 N 个元素.
如果是单个元素,那么每一个元素的平均代价就是 O (N)/N = O(1)
注意上面说的是并不代表每一个元素就是 O (1), 而是平均下来每一个是 O (1), 看下方例子就明白了
# 解决问题
- 只要每次让 L 和 R 让窗口保持大小为 w 就解决了
- 其他的和我们所说的都差不多
上面是最大值,最小值同理,都是反过来就行了
# 单调栈
例子:
-
有一个栈,因为我们关心的是更大,所以栈底到栈顶是从大到小的顺序,这个栈是用来存下标的 (为什么不存元素?因为存下标可以通过数组快速地获取到对应的值,存下标还可以给我们更多的信息)
-
遍历,如果这个元素
-
比我们栈顶的小,直接把下标放进去
-
比我们栈顶的大,把那个栈顶的元素弹出。注意!只要一个元素要弹出,他的信息就开始生成
- 他的左边最近比他大的就是他弹出的时候的栈底 (原本压被他压在下面的下标的元素), 如果本身就是栈底了,弹出之后没有元素了,那么说明左边最近比他大的元素为 null
- 他的右边最近比他大的就是此时我们要新加的元素,如果没有新加的元素 (到头了,但是栈里面还有元素) 那么就说明右边最近比他大的元素为 null
然后比较下一个,一直比到为空或者遇到比新加的元素值大的元素,我们才让这个新加的元素的下标加入到栈顶,或者遇到一样的直接让他们存在一个集合里面去
-
跟我们栈顶存的下标对应的元素一样,把下标压在一起,可以用集合,然后之后这个位置的存下标的集合弹出了,就会把里面所有的下标对应的元素都生成信息 (对于每一个下标对应的元素信息按照上面说的都一样的)
注意!!!如果一个集合多个下标元素,我们想要用它信息的时候用的是当前集合最后一个元素存的下标
-
这个跟上面的滑动窗口的双向队列的一样,时间复杂度是 O (N), 因为你这往右走的时候,走过 N 个元素,我们单调栈最多让 N 个元素弹出,最多让 N 个元素加入,所以代价就是 O (N) 级别,这个是对于 N 个元素.
如果是单个元素,那么每一个元素的平均代价就是 O (N)/N = O(1)
题目:
解法:
- 其实就是单调栈
- 看每个元素左边最近比自己小的,右边最近比自己小的,然后只扩到不包含那里 (这就保证了我们每一个元素只扩到比自己大的元素,最后形成的子数组就是最大指标累加是最大的)
# 大数据
# 布隆过滤器
比如说你想存 100 亿 url 都是黑名单 (其实这个跟爬虫去重问题一样), 每个 url64bytes
我们只需要加 url 以及查一个 url 存不存在这两个功能,且这个需要在内存,因为要是查硬盘存的那就时间太长了
如果要存到一个哈希表那就需要 6400 亿 bytes, 内存根本塞不下
所以我们可以使用布隆过滤器–>
布隆过滤器也是放在内存里面,使用空间很少
还有就是允许一定程度的失误率 (就是一个 url 在黑名单没查出来 (布隆过滤器不会有这种失误), 或者一个 url 不在黑名单结果查出是在黑名单里面 (布隆过滤器会有这种失误))
首先,bit 数组,就是每个元素就是一个比特,如何声明?
这里就是声明了一个长度为 320 比特的数组
现在想拿出下标为 178 的比特
这个 bit 是 1, 那么 s 就是 1, 如果这个 bit 是 0, 那么 s 就是 0
布隆过滤器就是一个超大的 bit 数组,假设 0-m-1, 那么总共就 m 个 bit, 也就是 m/8 个字节,很省空间
对于我们这个列子,对于每一个 url 我们对他调用多个哈希函数获得多个位置,接着就把 bit 数组对应的下标的值改黑 (0 变成 1or vice versa).
这样子之后想查一个数据,就会按照哈希函数找到所有对应的下标然后去看到底是不是全是被改成黑的,如果全是那么说明就是个黑名单的 url, 如果有起码一个没标成黑的,说明这个 url 不属于黑名单.
如果有一个 url 是黑名单 (之前已经加过了), 那就说明再查就一定全是黑的,所以这个错误不会发生
所以可能误判的问题就明显了,一个 url 经过多个哈希函数得到的下标,恰恰好就被之前其他多个 url 把那改为黑的,那么这个可能一看正好获得全是黑的,那么就会认为这个 url 也属于黑名单,其实并不
m–> 到底多大由你决定,越大失误率更小
k 个哈希函数–> 到底几个由你决定,这个要靠 m 的大小,并不是越多越好,越多一个 url 也会涂更多,所以还是要按照 m 的大小定一个合适的 k 最好
什么时候使用过滤器
- 在内存
- 是不是我们上面说的类似的结构–> 只是查询添加,没有删除的这种
- 允许一定失误率 (本来不在那上面的,结果返回结果还是在上面)
注意! 布隆过滤器只和 m 和 k 参数有关,单样本的大小随便,任何大的都行! 我们都会对他使用哈希函数等等等!!! 只要那个哈希函数可以接收那个数据的长度就可以!!!
== 单样本多大跟我们的布隆过滤器设计多大,设置多少个哈希函数,一点都没关系,只需要保证那个哈希函数可以接收那个长度的数据就可以了!!!==
三个公式:
然后这个 m 是 bits 的个数,我们 ÷8 可以得出多少个 bytes
对于 100 个 url 的例子,我们这里就是 26g (compared to 640g needed by hashset structrue), 内存不会被撑爆
如果有任何小数, 都向上取整 (比如说 m, 以及算出来的 k 等等等)
上面算出的 m 是理论的 (预期的), 如果面试官跟我们说可以更大,那么实际给的大小就是 m 真
然后 k 值按照那个 m 真算出的就叫做 k 真
我们可以用 m 真和 k 真算出实际的失误率 (肯定比我们的预期的失误率还低)
有了这个三个公式,我们只需要 n 的大小,以及允许多少失误率,就可以算出 m 和 k, 有了 m 我们就能知道多大,如果给我们的大小超过了我们算出的 m, 说明我们实际失误率还有机会更小 (也就是第三个公式的作用)
# 一致性哈希
如果使用分布式数据库,我们需要按照一个 key (用户给的,等等等) 算出他的哈希值,取模,然后去对应数据去找那个 key 对应的数据等等等
所以如果我们另外一个服务器被访问然后要求同一个 key 的数据,那个也会同样哈希函数然后取模到对应的数据库去
这个底层已经帮我们做好了,很均匀的分配到每一个数据库上
并且还能做到负载均衡,就是经常被查的 key 被均匀分到每一个数据库,然后 less 被查的也是均匀的分布,然后不怎么被查的 key 也是均匀的分布在所有数据库之中
__== 注意 key 一定需要是种类多的,这样就能保证高频,中频,低频 key 都是有一定数量的,那么根据哈希函数的性质就能做到均分,而不是使用那种比如说性别做 key, 只能是男女,所以就算多个数据库,我们这个 key 如果高频,只能被分到两个数据库里面去,一个存男这个 key 对应的数据,一个存女这个 key 对应的数据,不好!!!这会导致其他服务器负载低了,不好的 key 的设计。哈希 key 一定选择那种会有多个高频,多个中频,多个低频的那种数据最好 ==__这些就是底层一般帮你做好的,不需要你管
有个问题:
就比如说突然数据特别大,我们数据库不够用了,需要扩展更多的数据库,那么代表我们之前那个 (比如说图里的) 1,2,3 数据库里面的所有数据就需要重新哈希函数取模,然后获取到现在我们添加了其他数据库所对应的新位置
这个经典结构问题可见就是数据迁移问题,代价很大,一加服务器,所有数据都需要按照 key 重新哈希函数然后取模到现在新的位置才可以做到多个服务器之间平均分散
解决方法:
一致性哈希
想象哈希函数然后取模是一个圈,圈代表所有可能取到的值
- 我们对每一个数据库按照某个东西算出个哈希值然后取模
- 比如说有一个数据,我们按照 key 算出哈希值,然后取模
代码层次就是我们可以存每个数据库的哈希值取模的数,然后排序什么的
之后有数据我们算出哈希值然后取模,然后这个值拿来给我们的那个存数据库的哈希值取模的数那个集合里面进行二分查找,一直找到一个数最左且大于我们的这个数据 key 哈希值然后取模的值,我们就知道把当前数据存到哪个数据库了
这么做的好处就是我们加数据库机器,数据迁移很低
然后 m1,m2 服务器什么都不用干
同样道理,如果想要撤一个服务器,数据迁移代价也是很低:
但是这种方式有两个问题:
- 机器数量少的话,不能保证那些机器能把环均匀的平分开来,哈希函数保证的只是点的数量多起来之后,任何一段含有点的个数几乎是一样的,哈希函数可不是说我们这个三个数 m1,m2,m3 打到环上能做到均匀均分
- 即便我们机器很少还做到了均匀把环给分开,只要我们添加一台机器,或者减少一台机器,马上就能做到负载不均衡,这是因为
** 只要解决了这两个问题,一致性哈希就特别好用!!!**
解决方法:
虚拟节点技术
- 我们不是直接拿机器来算哈希然后取模了,而是每个机器给很多对应的虚拟节点,然后让虚拟节点去哈希值取模去抢环
- 这样数据迁移也很方便,比如说 a1000 代表的虚拟节点对应的哈希值取模后获取到对应的存储的数据至二级转给 b2 代表的虚拟节点对应的哈希值取模后对应的存储数据的地方 (虚拟节点给数据夺数据很简单很方便的操作)
- 此时这整个环,随便拿一块,这一块所有的 a 虚拟节点 (所属于 m1) 的哈希取模值,b 虚拟节点 (所属于 m2) 的哈希取模值,c 虚拟节点所属于 m3) 的哈希取模值都是差不多一样多的 (这个才是哈希函数保证的!)
- 同理我们想要加一个服务器,给他同样的数量的虚拟节点,让他们都哈希值取模,然后抢环,剩下的就是让别的数据库的虚拟节点里面对应的数据给到我们这个新添加的数据库的对应的虚拟节点对应的存储地方去就行了
此时我们环上,m1,m2,m3,m4 的虚拟节点都是差不多的,以及任何环上任何一段他们的数量都是差不多的
- 撤一台服务器,也是按照虚拟节点把数据给到对应的其他数据库的虚拟节点去,直到给广,都是很快的,给的也都很均匀
一致性哈希我们还可以,比如说某一个服务器性能更高,给他分配更多的虚拟节点,也就代表更多数据都会存到那个数据库去了,以及更多搜索查询等等等都会去那个数据库 (小声 bb 这不就是 nginx 的负载均衡功能吗)
一致性哈希算法在 1997 年由麻省理工学院提出,是一种特殊的哈希算法,在移除或者添加一个服务器时,能够尽可能小地改变已存在的服务请求与处理请求服务器之间的映射关系。一致性哈希解决了简单哈希算法在分布式哈希表(Distributed Hash Table,DHT)中存在的动态伸缩等问题
可以看出哈希函数的均匀的分布性是用处很大的!!!
# 大数据 (具体还是看视频)
简答解法就是用 bit 数组 (之前讲过用基础类型实现 bit array), 我们就是形成一个 232 长度的 bit 数组 (代表总共是 232/8 个字节,约 500MB, 所以内存 1G 够用), 每一个下标代表那个数有没有,如果有就让那个下标位置的变成 1 什么的,然后之后看哪个下标为 0 就代表那个数没有
但是进阶问题就需要:
首先看你内存能存多少空间,然后申请合理的 int 数组,接着把那 40 亿个整数挨个过一下,然后把那个范围到的数字都除你数组大小,然后对于每一个数让包含自己的那个范围的下标存的 count 加加,之后看哪个不达标继续让他自己分成几分几分的继续看,等等等
建议看视频 https://www.bilibili.com/video/BV13g41157hK?p=14&spm_id_from=pageDriver
1:45:00
# URL 大数据题目
一般按照下面的解法就没错,主要是多问,看看什么限制等等等
-
可以用哈希函数分流,把 100 个亿 URL 的大文件分流到很多个小文件或者是多台机器,通过哈希函数,每个 url 都获得一个哈希值,然后取模,因为哈希函数的性质,可以保证一种 URL 都会进一个文件。然后我们再对小文件里面统计有哪些重复的 URl (我们可以重复上面的操作,如果需要), 之后查出来再把信息汇总一下就行了
-
可以布隆过滤器,差不多道理,就是边添加的时候查询
补充部分的解法:
- 开始一样还是哈希函数分流到很多个小文件
- 我们对于每个小文件,数据量很少,我们可以用哈希表计算每个 url 以及他的词频 (count), 哪个词出现更多 count 就更大,然后把它形成一个大根堆,就是按照 count 次数来排序的大根堆
- 对每一个小文件都这么多,就好多个大根堆,如何合并他们实现所有文件之间出现最频繁的热门 100 词呢?
- 我们可以把每一个小文件维持的大根堆的堆顶拿出来,把他们都放进一个大根堆里面把这个大根堆叫做总堆
- 我们接着就可以从这个总堆里面拿数据,我们拿的这个数据来自于哪个小文件的大根堆就会让哪个小文件的大根堆里面的此时的堆顶出来加入到总堆里面去,这就相当于各个小文件里面最大的那个元素就行 pk, 然后一个数据走了会继续让那个小文件里面原本第二此时最大的 (出现次数的) 词汇加入到总堆里面进行 pk
因为都是堆,所以代价就是 log (n) 水平的,代价不高
就按照给的那七个看哪个合适,一般都是那之中的解法,还有哈希函数分流是万能的
# 位运算
# 1. 给定两个有符号 32 位整数 a 和 b,返回 a 和 b 中较大的
a * returnA+b*returnB ---------returnA 与 returnB 互斥,可用加法表达 if else
返回 a 的条件:
(1)if (a 和 b 符号不相同):a>0 返回 a
(2)if (a 和 b 符号相同):a-b>=0 返回 a
//请保证参数n,不是1就是0的情况下
//1-->0
//0-->1
public static int flip(int n) {
return n ^ 1;//按位异或
}
//n是非负数,返回1
//n是负数,返回0
public static int sign(int n) {
return flip((n >> 31) & 1);
}
//不考虑越界的解法
public static int getMax1(int a, int b) {
int c = a - b;
int scA = sign(c);//a-b为非负,scA为1;
int scB = flip(scA);//scA为0,scB为1;
//scA为0,scb必为1;scA为1,scB必为0
return a * scA + b * scB;
}
public static int getMax2(int a, int b) {
int c = a - b;
int sa = sign(a);
int sb = sign(b);
int sc = sign(c);
int difSab = sa ^ sb;//a和b的符号不一样,为1,一样为0
int sameSab = flip(difSab);//a和b的符号不一样,为0,一样为1
int returnA = difSab * sa + sameSab * sc;//返回a的条件:ab不一样且a是正的,ab一样且a-b>0
int returnB = flip(returnA);
return a * returnA + b * returnB; // 就是returnA跟returnB互斥,直接+的话,只会返回一个
}
public static void main(String[] args) {
int a = -16;
int b = 1;
System.out.println(getMax1(a, b));
System.out.println(getMax2(a, b));
a = 2147483647;
b = -2147480000;
System.out.println(getMax1(a, b)); // wrong answer because of overflow
System.out.println(getMax2(a, b));
} # 2. 给定 32 位正数,判断是否是 2 的幂,是否是 4 的幂
public static boolean is2Power(int n) {
return (n & (n - 1)) == 0;
}
//要满足n二进制只有一个1的情况,也就是n & (n - 1)) == 0
public static boolean is4Power(int n) {
return (n & (n - 1)) == 0 && (n & 0x55555555) != 0;
}# 3. 加减乘除
(1)加
public static int add(int a, int b) {
int sum = a;
while (b != 0) {
sum = a ^ b;
b = (a & b) << 1;
a = sum;
}
return sum;
}(2)减
public static int negNum(int n) {
return add(~n, 1);
}
public static int minus(int a, int b) {
return add(a, negNum(b));
}(3)乘
public static int multi(int a, int b) {
int res = 0;
while (b != 0) {
if ((b & 1) != 0) {
res = add(res, a);
}
a << = 1;
b >>>= 1; // 三个>>>代表无符号右移,最后会移没了
}
return res;
}(4) 除
# 暴力递归到动态规划
题目 —》找到暴力递归写法(尝试)
—》把可变参数,不讲究组织的形式,做缓存,那就是记忆化搜索的方法(拥有重复解的前提下)
—》精细化组织 ----》那就是动态规划
如果暴力过程中没有枚举行为(即通过循环来求得值)
则记忆化搜索和动态规划的时间复杂度一致,没有必要从记忆化搜索再优化为动态规划
# 什么暴力递归可以继续优化?
有重复调用同一个子问题的解,这种递归可以优化
如果每一个子问题都是不同的解,无法优化也不用优化
# 暴力递归和动态规划的关系
某一个暴力递归,有解的重复调用,就可以把这个暴力递归优化成动态规划
任何动态规划问题,都一定对应着某 - 个有解的重复调用的暴力递归
但不是所有的暴力递归,都一定对应着动态规划
# 面试题和动态规划的关系
解决一个问题,可能有很多尝试方法
可能在很多尝试方法中,又有若干个尝试方法有动态规划的方式
一个问题可能有若干种动态规划的解法
# 如何找到某个问题的动态规划方式?
1) 设计暴力递归:重要原则 + 4 种常见尝试模型!重点!
2) 分析有没有重复解:套路解决
3) 用记忆化搜索 -> 用严格表结构实现动态规划:套路解决
4) 看看能否继续优化:套路解决
# 面试中设计暴力递归过程的原则
1) 每一个可变参数的类型,一定不要比 int 类型更加复杂
2) 原则 1) 可以违反,让类型突破到一维线性结构,那必须是唯一 - 可变参数
3) 如果发现原则 1) 被违反,但不违反原则 2),只需要做到记忆化搜索即可
4) 可变参数的个数,能少则少
# 常见的 4 种尝试模型
1) 从左往右的尝试模型.
2) 范围上的尝试模型
3) 多样本位置全对应的尝试模型
4) 寻找业务限制的尝试模型
# 动态规划
暴力递归到动态规划
- 按照尝试方法暴力递归⬇️
- 记忆化搜索 (dp)⬇️
- 几个可变参数,就几维数组 (或其他)
- 可变参数挨个可能的值,然后数组 (或其他) 大小确保下标对应可以取的所有值
- 一开始初始化,把数组里面的值都设为什么,如果比如说 - 1 已经我们递归函数里面用了那就换一个我们递归函数不可能返回的等等等
- 在一开始或者 near the start (可能有直接返回一个数,比如说一个可变参数是负数直接返回 - 1 什么的,因为我们数组下标不可以是负数所以只能是直接返回一个 - 1 代表不可行) 写一个 if statement, 就是 dp [那个可变的参数在这一层当前值对应合适的下标][那个可变的参数在这一层当前值对应合适的下标][…]!=-1 或其他,就直接 return dp [那个可变的参数在这一层当前值对应合适的下标][那个可变的参数在这一层当前值对应合适的下标][…] 就行了
- 把这个作为参数传进递归函数,在 return XXX 的地方换成 dp [那个可变的参数当前值对应合适的下标][那个可变的参数当前值对应合适的下标][…]=XXX
- 严格表结构动态规划 (dp)⬇️
- 知道最终元素 (下标), 这个也就是我们当初暴力递归函数里面的可变参数的传进去的值 (从主函数里面的调用的时候)
- 根据我们递归函数里面的 base case 标出不用算直接可以获取答案的下标的那些元素
- 看依赖,就是我们递归函数的主体部分,每一个下标元素是跟哪一个下标的元素有依赖的等等等
- (按照上面发现的) 定出严格表到底是从哪些格子推倒哪些格子,最终来到重点位置
- 这个顺序定了,具体怎么求,递归代码里面 copy 过来,然后像记忆化搜索 (dp) 方式里面说的那些部分可以改成按照下标从 dp 里面拿值或者设值就可以了
- 然后最后返回数组中的一个格子的值,选择的格子一般都是我们那个最终元素 (下标), 不过看情况,有些可能会有什么开始的位置等等等,这个都是看你数据存的是什么和到底什么情况等等等–> 想要的究竟是什么
- 严格表结构精版本动态规划 (dp)
逻辑和业务其实只有在暴力递归尝试阶段已经完成了,之后都是用固定结构一步一步优化
# 机器人走路问题
给你标号为 1、2、3、……、N 的 N 个位置,机器人初始停在 S 位置上,走 K 步后停在 E 位置上的走法有多少种。注:机器人在 1 位置上时只能向右走,在 N 位置上时只能向左走,其它位置既可向右又可向左。
暴力递归方式:
暴力递归时间复杂度在最坏情况是 2k, 因为每一层可以左走或者右走,相当于一整个二叉树的可能,然后走 k 层相当于走二叉树的几层深度

有个问题:
可以看出暴力递归我们遇到一样的还是会再去把那一个展开再次执行,要是我们可以使用某种办法保存住那一块的信息,岂不是就不需要重新算了,发现是一样的直接用就行
这里是无后效性。无后效性是指对于递归中的某个子过程,其上级的决策对该级的后续决策没有任何影响
比如说上面
f(2,2)不管是f(3,1)还是f(3,3)调用的 (不管他的父级怎么样), 返回的结果都是一样的话,就是无后效性无后效性最适合动态规划
记忆化搜索做法:
首先我们知道我们有两个可变参数,那么就是一个二维表 (数组,可以用别的结构), 而数组大小就是每一个可变参数的最大是多少
而我们例子中
- 首先我们的当前位置是可变的,而这个的当前位置只能在 1 到 N, 所以我们干脆准备 N+1 个格子,就认为 0 是永远无法到达的
- 然后就是我们剩余步数 K, 值只会是 0 到 K, 也就是 K+1 大小的格子就够了
然后我们需要把这个二维数组所有数改为 - 1, 传过去
此时这个传过去的 dp 就相当于是缓存结构
此时我们之前的问题就不会发生了,所有重复的状态都不会一层一层让他完全运行的,而是看缓存里面要是有他的值,就直接用那个值就行了, 就是记得在所有你本来暴力递归你需要 return 的时候 (代表一层的答案) 的代码地方你都需要在 return 之间把那一层的答案赋值到当层可变参数作为 dp 数组下标的那个元素的值就行了 (就是看所有的 return 语句等然后再前面加上赋值操作等等等)
这种加了缓存的 dp 方法,这个 dp 数组是 K*N 的规模的,且在计算的时候,里面每一个元素最多只会计算一次,以后再遇到他都是返回的形式,对于每一个格子来说,如果邻近的格子是有东西的,他是 O (1) 的求解过程
所以时间复杂度就是 O (K*N)
严格表结构动态规划 (dp) 做法:
例子:

我们看递归里面:
这个就是说只有我们 k 步数剩余 0 的时候,如果等于了最后位置那么就是 1, 不然就是 0
这不就直接代表我们可以直接让 row 为 0 的,也就是代表剩余步数为 0 的那一行直接赋上值

目的就是看哪些能直接出答案的位置都给写好了
接着看递归:

我们可以看出我们每次 1 位置的都会依赖 2 位置的,注意依赖的是比自己那一层少一个步数的 2 位置

同理,接着看递归

同理,其他在中间的值,就是依赖左上角的值和右上角的值做累加
然后我们知道上面的各种关系之后,在这个问题里,我们可以直接按照那些边角的值,一个一个确认接下来的值,直接就可以把数组填满了 (其实填到我们那个标记着⭐️号的那个元素也就是我们开始位置,也就是我们最终答案,也就是从这个开始位置到那个结束位置走 K 步一共能有几个走法.

此时这个数组的每一个格子就相当于我们当初递归每一次每一层产生的结果.
注意这种严格表结构动态规划 (dp) 做法时间复杂度也是 O (K*N) 的
# 换钱的最小货币数量
题目:给定数组 arr,arr 中所有的值都为正数且可重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数 aim 代表要找的钱数,求取出最少个货币然后等于这个 aim 值。
举例:arr=[2,7,3,5,3],aim=10, 那么答案就是 7 和 3 两张货币,数量最小是 2.
暴力递归试法:从左到右
暴力递归代码:
此处返回 0 和返回 - 1 的含义不一样,返回 0 代表找到一个可能性 (就是几个元素加在一起等于 aim, 虽然不一样是最小数量的答案).
而返回 - 1 代表找不到,要么我们选这条路值超了,要么选这条路已经到头了还无法凑够,等等等
从左到右貌似都是
- 带上当前元素然后处理下一个
- 不带上当前元素然后处理下一个
然后就是各种 base case 等等等返回值的处理,然后最后选择貌似也都是 Math.min/Math.max 因为我们这里每一层都回调两次,然后这两次的返回结果中选一个想要的,一般是最大或者最小的
注意传的参数也一般都是那种还可以剩下多少什么什么的,等等等这里就是还可以剩下的多少的值等等等,然后你在回调的时候就把那个可变参数变化好才行
记忆化搜索动态规划写法:
然后其他就是一样的操作 (省略掉了), 就是注意我们 rest 可能是负数,而我们没法有负数下标的数组,所以我们可以留下一开始的如果 rest<0, 那就直接返回 - 1, 这个留着就代表这个路行不通的意思就行
严格表结构动态规划 (dp) 做法:
注意我们双维数组是按照什么顺序挨个填,是从上到下还是从下到上,是从左到右还是从右到左
可以直接把之前的递归函数里面的逻辑给拿过来,然后适当的用,也就是回调自己的地方用 dp 数组里面对应的下标的元素替代,然后原来那个递归函数里面的 return 语句替换成当前 dp 数组以及当前 dp 的下标来代表当前的值,也就是我们这次不是 return 返回代表这一层的返回值,而是给对应的位置的元素赋值成这一层的结果,就是注意我们数组下标可能越界的问题就行
# 两个聪明人拿牌问题递归到动态规划
范围上的模型
这里学到了
有些递归可变参数是两个下标,然后因为这两个下标一个是左边的一个是右边的,且左边下标不会超过右边下标
这就相当于让我们 dp 二维表 (如果是的话) 的下半三角变成不可用,因为那里的下标根本不符合我们定义的可变参数
- 有的题可能会需要两个 dp 数组等等等 (因为两个递归函数,然后他们互相递归调用)
- 如果递归函数 a 调用递归函数 b, 之后为了分析依赖关系建为表决定好哪个值依靠哪个之前的值以及按什么顺序把一个个格子得出来时,会需要让给 a 的 dp 依赖 b 的 dp 某个下标的值以及需要让给 b 的 dp 依赖 a 的 dp 某个下标的值,总之就是举个简单的例子,然后慢慢看,其实不难的,就挨个赋值一个先一个后什么的
# 暴力递归
public static int win1(int[] arr) {
if (arr == nu11|I arr.length == 0) {
return 0;
}
return Math . max(f(arr,0, arr.length - 1), s(arr, 0, arr .1ength - 1));
}
//先手
public static int f(int[] arr, int L, int R) {
if(L==R){
return arr[4];
}
return Math. max(
arr[L]+ s(arr, L + 1, R),arr[R] + s(arr, L, R - 1));
}
// 后手
public static int s(int[] arr, int i, int j) {
if (i=j) {
return 0;
}
return Math .min(f(arr, i + 1, j) //arr[i]
,f(arr, i, j - 1)); //arr[j]
}
# 动规
f 作为一张表缓存
s 作为一张表缓存
L>R 时,数据无效,即数组左下半区无效
/pic:mw://2c14ddb958445ac6716418d6047774b8
public static int win2(int[] arr) {
//进行过滤
if (arr == nu11|I arr.length == 0) {
return 0;
}
int N=arr.length;
int [][]f=new int[N][N];
int [][]f=new int[N][N];
for(int i=0;i<N;i++){
// if(L==R){
// return arr[L];
//}
f[i][i]=arr[i];
//if (i=j) {
//return 0;
//}
s[i][i]=0;
}
for(inti=1;i<N;i++){
int L =0;
int R =i;
while(L<N&&R<N){
//f[row][col] = ?;
//return Math. max(arr[L]+ s(arr, L + 1, R),arr[R] + s(arr, L, R - 1));
f[L][R] = Math . max(
arr[L] + s[L + 1][ R],
arr[R] + s[L][R - 1]
);
//return Math .min(f(arr, i + 1, j) //arr[i] ,f(arr, i, j - 1)); //arr[j]
s[L][R] = Math.min(
f[L + 1][R], // arr[i]
f[L][R - 1] // arr[j]
);
L++;
R++;
}
}
//return Math . max(f(arr,0, arr.length - 1), s(arr, 0, arr .1ength - 1));
return Math.max(f[0][arr.length - 1]
,s[0][arr.length - 1]
);
}
# 马走棋盘问题
马从(0,0)出发,到达指定的(x,y)位置,必须走 k 步数,一共有多少种方法?
(马只能走日)
对于每个点,到达他的位置有 8 个位置(不越界的前提下)
这里学到了 dp 可以是三维的甚至更多… 都差不多
突然发现这种有几种方式,或者所有方式最少最多最小最大什么什么的这种本来就需要获取到所有方式才可以决定的都是需要暴力递归,然后改成动态规划
# 暴力递归
public static int f(int х,int y,int k){
if(k ==0) {
returnх==0&&y==0?1:0;
}
if(x_ < 0 || х> 9 || у<0 || у>8) {
return 0;
}
//有步数要走,x,y也是棋盘上的位置
return
f (x+2,y-1, k-1)
+f(x + 2, y+1, k-1)
+ f(х+1,y+2,k-1)
+f(x-1,у+2,k-1)
+ f(x- 2,y+1,k-1)
+f(x - 2, y-1, k-1)
+ f(x-1,y-2,k-1)
+f(x + 1, у-2, k-1);
}
# 改动态规划
因为是后一步依赖前一步,所以先准备第一步的数据,逐步往前,直到最后一步。
public static int ways2(int x, int y, int k) {
int[][][] dp = new int[10][9][k+1];// O~k
dp[0][0][0] = 1; // dp[..][..][0] = 0
for(int level = 1; level <= k; level++) {
for(int x =0;x<10;x++){//x可能性
for(int y =0; y < 9;y++){
// 求 dp[i][j][level]; 递归函数怎么求的。这里也怎么求
dp[i][j][level]=
getValue(dp,x+2,y-1, level-1)
+getValue(dp,x + 2, y+1, level-1)
+getValue(dp,х+1,y+2,level-1)
+getValue(dp,x-1,у+2,level-1)
+getValue(dp,x- 2,y+1,level-1)
+getValue(dp,x - 2, y-1, level-1)
+getValue(dp,x-1,y-2,level-1)
+getValue(dp,x + 1, у-2, level-1);
;
}
}
}
return dp[x][y][k];
}
public static int getValue(int[][][] dp, int x, int y, int k) {
if(x<0 || x>9 || y<0 || y>8){
return 0;
}
return dp[x][y][k];
}
# bob 活着
题目:给定范围横向 N,纵向 M,从(i,j)开始走 K 步(只能上下左右走,且概率相同)没有超过给定范围那么就是活着,如果在过程中超过了范围则死了,返回活着的概率。
在这个题里面,每一个点 bob 都可以走上下左右,然后可以走 k 步,那么总共的可能步数是 4k, 之后获得了总共的活着的次数,用那个次数 / 4k 等等等就可以获取答案了
递归实现
public class Main {
public static int N, M;
public static String process(int n, int m, int i, int j, int k) {
N = n;
M = m;
int live = process(i, j, k);// 活着的情况
int all = (int) Math.pow(4, k);// 一共存在的情况
int gcb = gcb(all, live);// 求最大公约数
return live / gcb + " / " + all / gcb;
}
private static int gcb(int m, int n) {
if (n == 0) return m;
return gcb(n, m % n);
}
// 计算活着的情况数
public static int process(int i, int j, int K) {
if (i < 1 || i > N || j < 1 || j > M) return 0;
if (K == 0) return 1;
return process(i + 1, j, K - 1) +
process(i - 1, j, K - 1) +
process(i, j + 1, K - 1) +
process(i, j - 1, K - 1);
}
}严格表结构
class U {
public static long gcd(long m, long n) {
return n == 0 ? m : gcd(n, m % n);
}
public static String bob2(int N, int M, int i, int j, int K) {
int[][][] dp = new int[N + 2][M + 2][K + 1];
for (int row = 1; row <= N; row++) {//初始化数据
for (int col = 1; col <= M; col++) {
dp[row][col][0] = 1;
}
}
for (int rest = 1; rest <= K; rest++) {
for (int row = 1; row <= N; row++) {
for (int col = 1; col <= M; col++) {
//递归依赖
dp[row][col][rest] = dp[row - 1][col][rest - 1];
dp[row][col][rest] += dp[row + 1][col][rest - 1];
dp[row][col][rest] += dp[row][col - 1][rest - 1];
dp[row][col][rest] += dp[row][col + 1][rest - 1];
}
}
}
long all = (long) Math.pow(4, K);
long live = dp[i + 1][j + 1][K];
long gcd = gcd(all, live);
return (live / gcd) + "/" + (all / gcd);
}
}# 拿钞票问题递归到动态规划
一个数组,里面的元素代表钞票面额,每种钞票都可以无穷次的拿,数组中无重复值、均为正数
给一个目标值,求用数组中有多少种办法将目标值凑出来?
有重复的,我们使用从左到右模型,可变参数用的是当前要处理的元素的 index 和 rest (一般都差不多)
注意每个元素可重复,所以我们直接把递归放到 for 循环里面,让他循环合理的次数就行,然后在每次循环都是普通的该怎么调用怎么调用,注意!!!
for 循环开始和结束值只要设置好,那么只要在里面简单的递归调用下一个位置的元素就就行了,比如说下面这个例子里面
- 一开始是 0, 所以相当于是调用给下一个元素而且不包括当前元素 (这个直接多给你弄好了,就不需要你弄两个递归什么的了,意思都一样,for 循环嘛!)
- 然后是 1 (这个列子里面) 代表当前下标的元素用了一次,然后调用下一个下标的元素
- 然后是 2 (这个列子里面) 代表当前下标的元素用了两次,然后调用下一个下标的元素
- …
- 然后是 N (这个列子里面,当然这个 N 的数量应该按照另外一个可变参数等等等获取到一个合理的数量,这里就是
zhang * arr[index] <= rest很合理,zhang 数 (for 循环最终值) 就应该是这样决定的) 代表当前下标的元素用了 N 次,然后调用下一个下标的元素注意!
if(index == arr.length) { return rest ==0?1 :0 ; }这一块,我们还需要在里面测一下 rest 是不是等于 0 了,这是为了考虑数组最后一个元素,因为在数组最后一个元素的 index 的那一次递归的时候,他接着调用,就会调用 index+1, 此时他调用的递归的 index 就会是 arr.length, 我们需要在这里也要考虑 rest 是不是剩余 0 了,也就是考虑了数组最后一个值
==_从左到右或者类似的都需要考虑这个_最后一个元素,以及各种可能会出界等等等的问题!!!__==
- 这里还介绍了如果递归函数里面有枚举行为,该怎么用 dp 优化,我们可以把那个枚举的循环直接放到我们那个 dp 表结构的多重循环里面,不过这样稍微时间复杂度有点高
不过我们可以再次优化,仔细观查每一个格子的依赖,看看有没有依赖于其他的格子,这个例子里面就发现一个列子如果同一行有数据了,我们可以更方便获取到那个格子的 value, 我们可以再次优化让他省掉那个循环,让 dp 表结构方法边的更快
== 注意只要之后在填表的时候,如果有枚举行为,就观察方式看看邻近的位置能不能替代枚举行为,只跟观察有关,** 跟原题没关!!!**==
- 注意 dp 方式,一定一定一定要
- 保证可变参数越少越好 (dp 数组维度也可以减少)
- 保证可变参数最好只是一个整数什么的 (别整一个数组或者链表等等等,太多可能性了,dp 表很难表示)
暴力递归
// arr中都是正数且无重复值,返回组成aim的方法数
public static int ways(int[] arr, int aim) {
if(arr==nu1l||arr.length=0||aim<0){
return 0;
}
return process(arr, 0, aim);
}
//可以自由使用arr[index... ]所有的面值,每一种面值都可以使用任意张,
//组成rest,有多少种方法
public static int process(int[] arr, int index, int rest) {
if(index == arr.length) {
return rest ==0?1 :0 ;
}
int ways = 0;
for(int zhang = 0;zhang * arr[index] <= rest ;zhang++) {
ways += process(arr, index + 1, rest - (zhang * arr[index]) );
}
return ways;
}有重复过程,所以有必要优化
记忆 dp
public static int ways2(int[] arr, int aim) {
if (arr == nu1l || arr .1ength == 0|1 aim < 0) {
return 0;
}
int[][] dp = new int[arr .1ength+1][aim+1];
//一开始所有的过程,都没有计算呢
// dp[..][..]
= -1
for(int i = 0 ; i < dp.1ength; i++) {
for(int j = 0 ; j < dp[8].1ength; j++) {
dp[i][j] = -1;
}
}
return process2(arr, 0,aim,dp);
}
//如果index和rest的参数组合,是没算过的,dp[index][rest]:== -1
//如果index和rest的参数组合,是算过的,dp[index][rest]> -1
public static int process(int[] arr, int index, int rest,int [][]dp) {
if(dp[index][rest] != -1) {
return dp[index][rest];
}
if(index == arr.1ength) {
dp[index][rest]=rest ==0?1 :0 ;
//return rest ==0?1 :0 ;
return dp[index][rest];
}
int ways = 0;
for(int zhang = 0;zhang * arr[index] <= rest ;zhang++) {
ways += process(arr, index + 1, rest - (zhang * arr[index]),dp );
}
// 进行缓存
dp[index][rest]=ways;
return ways;
}动态规划
由下到上进行计算,每一行从左往右
public static int ways2(int[] arr, int aim) {
if (arr == nu1l || arr .1ength == 0|| aim < 0) {
return 0;
}
int N=arr.length;
int[][] dp = new int[N+1][aim+1];
//一开始所有的过程,都没有计算呢
// dp[..][..]= -1
//if(index == arr.1ength) {
// return rest ==0?1 :0 ;
//}
dp[N][0]=1;//dp[N][1...aim]=0;
for(int index = N - 1; index >= 0; index--) {
for(int rest = 0; rest <= aim; rest++) {
//dp[index][rest] = ?;
int ways = 0;
for(int zhang = 0;zhang * arr[index] <= rest ;zhang++) {
ways += dp[index + 1][rest - (zhang * arr[index])];
}
dp[index][rest] = ways;
}
}
return dp[0][aim];
}这种时间复杂度是 O (N*aim2) 的
因为有枚举行为,可以进行优化
比如,f(3,100) 其实是依赖 f(3,97)的
–> f (3,100) 和 f (3,97) 都在一行上,都是面值代表是 3, 然后我们的 f (3,100) 其实就是下一行 (多少多少面值) 的 a 值 + b 值 + c 值等等等,但是我们已经算出 f (3,97) 的话我们知道 f (3,97) 的值是 b 值 + c 值等等等算出来的,所以我们只需要 a 值 + f (3,97) 的值就可以获取到 f (3,100) 的值,压根不需要重新让一个一个加到头了
tip: 到了 dp 之后就不需要想原本的逻辑,就按照我们那种改法都改成 dp 表结构之后,然后再从依赖关系出发看看还能有什么优化等等等
所以可以更进一步优化:
public static int ways2(int[] arr, int aim) {
if (arr == nu1l || arr .1ength == 0|1 aim < 0) {
return 0;
}
int N=arr.length;
int[][] dp = new int[N+1][aim+1];
//一开始所有的过程,都没有计算呢
// dp[..][..]= -1
//if(index == arr.1ength) {
// return rest ==0?1 :0 ;
//}
dp[N][0]=1;//dp[N][1...aim]=0;
for(int index = N - 1; index >= 0; index--) {
for(int rest = 0; rest <= aim; rest++) {
//dp[index][rest] = ?;
dp[index][rest] = dp[index+1][rest];
if(rest-arr[index]>=0){
dp[index][rest]+=dp[index][rest-]
}
}
}
return dp[0][aim];
}# 有序表
跟哈希表很像,只不过能保证 key 有序,所有操作,增删改查都是 **O (logN)** 级别的
可以实现有序表的结构:
- 红黑树
- AVL 树
- Self Balancing Tree
上面都是 BST,balancing search tree, 他们实现的有序表时间复杂度都差不多,只是常数的区别
- Skip List (跳表)
# Balancing Search Tree
首先搜索二叉树是一般没有重复元素的,不过要是想有或者想让每个节点多保存某种信息什么的完全可以,就是在节点类里面加属性呗, 相当于就算是有重复值我们也可以做压缩,所以其实就可以默认我们 BST 是没有重复的
# 平衡二叉树 / AVL 树
# 平衡性
经典的平衡二叉树结构:在满足搜索二叉树的前提条件下,对于一棵二叉树中的任意子树,其左子树和其右子树的高度相差不超过 1。
# 典型搜索二叉树 ——AVL 树、红黑树、SBT 树的原理
# AVL 树
AVL 树是一种具有严苛平衡性的搜索二叉树。什么叫做严苛平衡性呢?那就是所有子树的左子树和右子树的高度相差不超过 1。弊端是,每次发现因为插入、删除操作破坏了这种严苛的平衡性之后,都需要作出相应的调整以使其恢复平衡,调整较为频繁。
# 红黑树
红黑树是每个节点都带有颜色属性的搜索二叉树,颜色或红色或黑色。在搜索二叉树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 性质 1. 节点是红色或黑色。
- 性质 2. 根节点是黑色。
- 性质 3 每个叶节点(NIL 节点,空节点)是黑色的。
- 性质 4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 性质 5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
要知道为什么这些特性确保了这个结果,注意到性质 4 导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据性质 5 所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
# SBT 树
它是由中国广东中山纪念中学的陈启峰发明的。陈启峰于 2006 年底完成论文《Size Balanced Tree》,并在 2007 年的全国青少年信息学奥林匹克竞赛冬令营中发表。相比红黑树、AVL 树等自平衡二叉查找树,SBT 更易于实现。据陈启峰在论文中称,SBT 是 “目前为止速度最快的高级二叉搜索树”。SBT 能在 O (log n) 的时间内完成所有二叉搜索树 (BST) 的相关操作,而与普通二叉搜索树相比,SBT 仅仅加入了简洁的核心操作 Maintain。由于 SBT 赖以保持平衡的是 size 域而不是其他 “无用” 的域,它可以很方便地实现动态顺序统计中的 select 和 rank 操作。
SBT 树的性质是:对于数中任意结点,以该结点为根节点的子树的结点个数不能比以该结点的叔叔结点为根节点的子树的结点个数大。
# 旋转 ——Rebalance
左旋:
右旋:
每种平衡二叉树都有自己的一套在插入、删除等操作改变树结构而破坏既定平衡性时的应对措施(但都是左旋操作和右旋操作的组合),以 AVL 数为例(有四种平衡调整操作,其中的数字只是结点代号而非结点数值):
-
LL 调整:2 号结点的左孩子的左孩子导致整个树不平衡,2 号结点右旋一次
-
RR 调整:3 号结点的右孩子的右孩子导致树不平衡,3 号结点左旋一次:
-
LR 调整:先左后右
-
RL 调整:先右后左:
红黑树的调整也是类似的,只不过调整方案更多。面试中一般不会让你手写红黑树(若有兴趣可参见文末附录),但我们一定能说清这些查找二叉树的性质,以及调整平衡的基本操作,再就是这些结构的使用。
# Java 中红黑树的使用
Java 中红黑树的实现有 TreeSet 和 TreeMap,前者结点存储的是单一数据,而后者存储的是 `` 的形式。
public static void main(String[] args) {
TreeMap treeMap = new TreeMap();
treeMap.put(5, "tom");
treeMap.put(11, "jack");
treeMap.put(30,"tony");
treeMap.put(18, "alice");
treeMap.put(25, "jerry");
//红黑树中最右边的结点
System.out.println(treeMap.lastEntry());
System.out.println(treeMap.lastKey());
//红黑树最左边的结点
System.out.println(treeMap.firstKey());
//如果有13这个key,那么返回这条记录,否则返回树中比13大的key中最小的那一个
System.out.println(treeMap.ceilingEntry(13));
//如果有21这个key,那么返回这条记录,否则返回树中比21小的key中最大的那一个
System.out.println(treeMap.floorEntry(21));
//比11大的key中,最小的那一个
System.out.println(treeMap.higherKey(11));
//比25小的key中,最大的那一个
System.out.println(treeMap.lowerKey(25));
//遍历红黑树,是按key有序遍历的
for (Map.Entry record : treeMap.entrySet()) {
System.out.println("age:"+record.getKey()+",name:"+record.getValue());
}
}TreeMap 的优势是 key 在其中是有序组织的,因此增加、删除、查找 key 的时间复杂度均为 log (2,N)。
# 案例
# The Skyline Problem
水平面上有 N 座大楼,每座大楼都是矩阵的形状,可以用一个三元组表示 (start, end, height),分别代表其在 x 轴上的起点,终点和高度。大楼之间从远处看可能会重叠,求出 N 座大楼的外轮廓线。
外轮廓线的表示方法为若干三元组,每个三元组包含三个数字 (start, end, height),代表这段轮廓的起始位置,终止位置和高度。
给出三座大楼:
[
[1, 3, 3],
[2, 4, 4],
[5, 6, 1]
]外轮廓线为:
[
[1, 2, 3],
[2, 4, 4],
[5, 6, 1]
]解析:
1. 将一座楼的表示 [start,end,height] 拆分成左右两个边界(边界包含:所处下标、边界高度、是楼的左边界还是右边界),比如 [1,3,3] 就可以拆分成 [1,3,true] 和 [3,3,false] 的形式(true 代表左边界、false 代表右边界)。
2. 将每座楼都拆分成两个边界,然后对边界按照边界所处的下标进行排序。比如 [[1,3,3],[2,4,4],[5,6,1] 拆分之后为 [[1,3,true],[3,3,false],[2,4,true],[,4,4,false],[5,1,true],[6,1,false]],排序后为 [[1,3,true],[2,4,true],[3,3,false],[4,4,false],[5,1,true],[6,1,false]]
3. 将边界排序后,遍历每个边界的高度并依次加入到一棵 TreeMap 红黑树中(记为 countOfH),以该高度出现的次数作为键值(第一次添加的高度键值为 1),如果遍历过程中有重复的边界高度添加,要判断它是左边界还是右边界,前者直接将该高度在红黑树中的键值加 1,后者则减 1。以步骤 2 中排序后的边界数组为例,首先判断 countOfH 是否添加过边界 [1,3,true] 的高度 3,发现没有,于是 put (3,1);接着对 [2,4,true],put [4,1];然后尝试添加 [3,3,false] 的 3,发现 countOfH 中添加过 3,而 [3,3,false] 是右边界,因此将 countOfH.get (3) 的次数减 1,当 countOfH 中的记录的键值为 0 时直接移除,于是移除高度为 3 的这一条记录;……
对于遍历过程经过的每一个边界,我们还需要一棵 TreeMap 红黑树(记为 maxHOfPos)来记录对我们后续求外轮廓线有用的信息,也就是每个边界所处下标的最大建筑高度:
这里有个细节要注意一下,那就是如果添加某个边界之后,countOfH 树为空了,那么该边界所处下标的建筑高度要记为 0,表示一片相邻建筑的结束,比如上图中下标为 4 和 6 的边界。这也是为了后续求外轮廓线提供判断的依据。
4. 遍历 maxHOfPos 中的记录,构造整个外轮廓线数组:
起初没有遍历边界时,记 start=0,height=0,接着遍历边界,如果边界高度 curHeight!=height 如上图中的 1->2:height=0,curHeight=3,那么记 start=1,height=3 表示第一条组外轮廓线的 start 和 height,接下来就是确定它的 end 了。确定了一条轮廓线的 start 和 height 之后会有两种情况:下一组轮廓线和这一组是挨着的(如上图 2->3)、下一组轮廓线和这一组是相隔的(如上图中 3->4)。因此在遍历到边界 [index:2,H:4] 时,发现 curHeight=4 != height=3,于是可以确定轮廓线 start:1,heigth:3 的 end:2。确定一条轮廓线后就要更新一下 start=2,heigth=4 表示下一组轮廓线的起始下标和高度,接着遍历到边界 [index:3,H:4],发现 curHeight=4=height 于是跳过;接着遍历到边界 [index:4,H:0],发现 curHeight=0,根据步骤 3 中的逻辑可知一片相邻的建筑到此结束了,因此轮廓线 start:2,height:4 的 end=4。
示例代码:
package top.zhenganwen.lintcode;
import java.util.*;
public class T131_The_SkylineProblem {
public class Border implements Comparable {
public int index;
public int height;
public boolean isLeft;
public Border(int index, int height, boolean isLeft) {
this.index = index;
this.height = height;
this.isLeft = isLeft;
} <a href="/profile/992988" data-card-uid="992988" class="" target="_blank" from-niu="default" data-card-index="8">@Override public int compareTo(Border border) {
if (this.index != border.index) {
return this.index - border.index;
}
if (this.isLeft != border.isLeft) {
return this.isLeft ? -1 : 1;
}
return 0;
}
}
/**
* @param buildings: A list of lists of integers
* @return: Find the outline of those buildings
*/
public List> buildingOutline(int[][] buildings) {
//1、split one building to two borders and sort by border's index
Border[] borders = new Border[buildings.length * 2];
for (int i = 0; i < buildings.length; i++) {
int[] oneBuilding = buildings[i];
borders[i * 2] = new Border(oneBuilding[0], oneBuilding[2], true);
borders[i * 2 + 1] = new Border(oneBuilding[1], oneBuilding[2], false);
}
Arrays.sort(borders);
//2、traversal borders and record the max height of each index
//key->height value->the count of the height
TreeMap countOfH = new TreeMap();
//key->index value->the max height of the index
TreeMap maxHOfPos = new TreeMap();
for (int i = 0; i < borders.length; i++) {
int height = borders[i].height;
if (!countOfH.containsKey(height)) {
countOfH.put(height, 1);
}else {
int count = countOfH.get(height);
if (borders[i].isLeft) {
countOfH.put(height, count + 1);
} else {
countOfH.put(height, count - 1);
if (countOfH.get(height) == 0) {
countOfH.remove(height);
}
}
}
if (countOfH.isEmpty()) {
maxHOfPos.put(borders[i].index, 0);
} else {
//lastKey() return the maxHeight in countOfH RedBlackTree->log(2,N)
maxHOfPos.put(borders[i].index, countOfH.lastKey());
}
}
//3、draw the buildings outline according to the maxHOfPos
int start = 0;
int height = 0;
List> res = new ArrayList();
for (Map.Entry entry : maxHOfPos.entrySet()) {
int curPosition = entry.getKey();
int curMaxHeight = entry.getValue();
if (height != curMaxHeight) {
//if the height don't be reset to 0,the curPosition is the end
if (height != 0) {
List record = new ArrayList();
record.add(start);
record.add(curPosition);//end
record.add(height);
res.add(record);
}
//reset the height and start
height = curMaxHeight;
start = curPosition;
}
}
return res;
}
public static void main(String[] args) {
int[][] buildings = {
{1, 3, 3},
{2, 4, 4},
{5, 6, 1}
};
System.out.println(new T131_The_SkylineProblem().buildingOutline(buildings));
}
}# 跳表
跳表有着和红黑树、SBT 树相同的功能,都能实现在 O (log (2,N)) 内实现对数据的增删改查操作。但跳表不是以二叉树为原型的,其设计细节如下:
记该结构为 SkipList,该结构中可以包含有很多结点(SkipListNode),每个结点代表一个被添加到该结构的数据项。当实例化 SkipList 时,该对象就会自带一个 SkipListNode(不代表任何数据项的头结点)。
# 添加数据
当你向其中添加数据之前,首先会抛硬币,将第一次出现正面朝上时硬币被抛出的次数作为该数据的层数(level,最小为 1),接着将数据和其层数封装成一个 SkipListNode 添加到 SkipList 中。结构初始化时,其头结点的层数为 0,但每次添加数据后都会更新头结点的层数为所添数据中层数最大的。比如实例化一个 SkipList 后向其中添加一条层数为 3 的数据 7:
这时如果再添加一条层数为 2 的数据 5 呢?首先游标 curNode 会从 head 的最高层出发往右走,走到数据项为 7 的结点,发现 7>5,于是又退回来走向下一层:
接着再尝试往右走,还是发现 7>5,于是还是准备走向下一层,但此时发现 curNode 所在层数 2 是数据项 5 的最高层,于是先建出数据项 5 的第二层,curNode 再走向下一层:
同样的,curNode 尝试往右走,但发现 7>5,curNode 所在层为 1,但数据 5 的第一层还没建,于是建出,curNode 再往下走。当 curNode 走到 null 时,建出数据 5 根部的 null:
至此层数为 2 的数据项 5 的添加操作完毕。
那如果添加一个层数较高的数据项该如何处理呢?以添加层数为 4 的数据 10 为例:
添加操作对应的代码示例:
import java.util.ArrayList;
/**
* A stored structure.Its add,delete,update,find operation are log(2,N)
*
* @author zhenganwen
*/
public class SkipList {
private SkipListNode head;
private int maxLevel;
private int size;
public static final double PROBABILITY = 0.5;
public SkipList() {
this.head = new SkipListNode(Integer.MIN_VALUE);
/**
* the 0th level of each SkipListNode is null
*/
this.head.nextNodes.add(null);
this.maxLevel = 0;
this.size = 0;
}
private class SkipListNode {
int value;
/**
* nextNodes represent the all levels of a SkipListNode the element on
* one index represent the successor SkipListNode on the indexth level
*/
ArrayList nextNodes;
public SkipListNode(int newValue) {
this.value = newValue;
this.nextNodes = new ArrayList();
}
}
/**
* put a new data into the structure->log(2,N)
*
* @param newValue
*/
public void add(int newValue) {
if (!contains(newValue)) {
// generate the level
int level = 1;
while (Math.random() < PROBABILITY) {
level++;
}
// update max level
if (level > maxLevel) {
int increment = level - maxLevel;
while (increment-- > 0) {
this.head.nextNodes.add(null);
}
maxLevel = level;
}
// encapsulate value
SkipListNode newNode = new SkipListNode(newValue);
// build all the levels of new node
SkipListNode cur = findInsertionOfTopLevel(newValue, level);
while (level > 0) {
if (cur.nextNodes.get(level) != null) {
newNode.nextNodes.add(0, cur.nextNodes.get(level));
} else {
newNode.nextNodes.add(0, null);
}
cur.nextNodes.set(level, newNode);
level--;
cur = findNextInsertion(cur, newValue, level);
}
newNode.nextNodes.add(0, null);
size++;
}
}
/**
* find the insertion point of the newNode's top level from head's maxLevel
* by going right or down
*
* @param newValue newNode's value
* @param level newNode's top level
* <a href="/profile/547241" data-card-uid="547241" class="" target="_blank" from-niu="default" data-card-index="9">@return */
private SkipListNode findInsertionOfTopLevel(int newValue, int level) {
int curLevel = this.maxLevel;
SkipListNode cur = head;
while (curLevel >= level) {
if (cur.nextNodes.get(curLevel) != null
&& cur.nextNodes.get(curLevel).value < newValue) {
// go right
cur = cur.nextNodes.get(curLevel);
} else {
// go down
curLevel--;
}
}
return cur;
}
/**
* find the next insertion from cur node by going right on the level
*
* @param cur
* @param newValue
* @param level
* </a><a href="/profile/547241" data-card-uid="547241" class="" target="_blank" from-niu="default" data-card-index="10">@return */
private SkipListNode findNextInsertion(SkipListNode cur, int newValue,
int level) {
while (cur.nextNodes.get(level) != null
&& cur.nextNodes.get(level).value < newValue) {
cur = cur.nextNodes.get(level);
}
return cur;
}
/**
* check whether a value exists->log(2,N)
*
* @param value
* </a><a href="/profile/547241" data-card-uid="547241" class="" target="_blank" from-niu="default" data-card-index="11">@return */
public boolean contains(int value) {
if (this.size == 0) {
return false;
}
SkipListNode cur = head;
int curLevel = maxLevel;
while (curLevel > 0) {
if (cur.nextNodes.get(curLevel) != null) {
if (cur.nextNodes.get(curLevel).value == value) {
return true;
} else if (cur.nextNodes.get(curLevel).value < value) {
cur = cur.nextNodes.get(curLevel);
} else {
curLevel--;
}
} else {
curLevel--;
}
}
return false;
}
public static void main(String[] args) {
SkipList skipList = new SkipList();
skipList.add(1);
skipList.add(2);
skipList.add(3);
skipList.add(4);
skipList.add(5);
//mark a break point here to check the memory structure of skipList
System.out.println(skipList);
}
}# 查找数据
查找数据项的操作和添加数据项的步骤类似,也是游标 curNode 从 head 的最高层出发,每次先尝试向右走来到 nextNode,如果 nextNode 封装的数据大于查找的目标 target 或 nextNode 为空,那么 curNode 回退并向下走;如果 nextNode 封装的数据小于 target,那么 curNode 继续向右走,直到 curNode 走到的结点数据与 target 相同表示找到了,否则 curNode 走到了某一结点的根部 null,那么说明结构中不存在该数据。->contains ()
# 删除数据
了解添加数据的过程之后,删除数据其实就是将逻辑倒过来:解除该数据结点的前后引用关系。下图是我在写好上述 add () 方法后,向其中放入 1、2、3、4、5 后形成的结构:
如果此时删除数据 3:
首先应该从 head 的最高层出发,通过向右或向下找到数据 3 的最高层(如图 2->3->5->6->7),将该层移除整体结构并处理好该层上,其前后结点的关系。同样的逻辑,将数据 3 剩下的层移除。
示例代码:
/**
* delete skipListNode by the value
*
* @param value
*/
public void delete(int value) {
//if exists
if (contains(value)) {
//find the node and its level
SkipListNode deletedNode = head;
int deletedLevels = maxLevel;
//because exists,so must can find
while (deletedLevels > 0) {
if (deletedNode.nextNodes.get(deletedLevels) != null) {
if (deletedNode.nextNodes.get(deletedLevels).value == value) {
deletedNode = deletedNode.nextNodes.get(deletedLevels);
break;
} else if (deletedNode.nextNodes.get(deletedLevels).value < value) {
deletedNode = deletedNode.nextNodes.get(deletedLevels);
} else {
deletedLevels--;
}
} else {
deletedLevels--;
}
}
//release the node and adjust the reference
while (deletedLevels > 0) {
SkipListNode pre = findInsertionOfTopLevel(value, deletedLevels);
if (deletedNode.nextNodes.get(deletedLevels) != null) {
pre.nextNodes.set(deletedLevels, deletedNode.nextNodes.get(deletedLevels));
} else {
pre.nextNodes.set(deletedLevels, null);
}
deletedLevels--;
}
size--;
}
}
public static void main(String[] args) {
SkipList skipList = new SkipList();
skipList.add(1);
skipList.add(2);
skipList.add(3);
skipList.add(4);
skipList.add(5);
//mark a break point here to check the memory structure of skipList
skipList.delete(3);
System.out.println(skipList);
}# 遍历数据
需要遍历跳表中的数据时,我们可以根据每个数据的层数至少为 1 的特点(每个结点的第一层引用的是比该结点数据大的结点中数据最小的结点)。
示例代码:
class SkipListIterator implements Iterator {
private SkipListNode cur;
public SkipListIterator(SkipList skipList) {
this.cur = skipList.head;
}
@Override
public boolean hasNext() {
return cur.nextNodes.get(1) != null;
}
@Override
public Integer next() {
int value = cur.nextNodes.get(1).value;
cur = cur.nextNodes.get(1);
return value;
}
}
@Override
public String toString() {
SkipListIterator iterator = new SkipListIterator(this);
String res = "[ ";
while (iterator.hasNext()) {
res += iterator.next()+" ";
}
res += "]";
System.out.println();
return res;
}
public static void main(String[] args) {
SkipList skipList = new SkipList();
skipList.add(1);
skipList.add(2);
skipList.add(3);
skipList.add(4);
skipList.add(5);
System.out.println(skipList);
skipList.delete(3);
System.out.println(skipList);
}# 刷题以及技巧
# 题目
# 绳子覆盖
解法:
贪心 + 二分
-
把数组中每一个点都作为绳子的右端,有多少点就有多少种方式,之后答案肯定在这其中
-
贪心策略,把绳子右端放到点的位置上,而不要放没点的位置上
-
比如说数组 [2,4,8,9], 绳子长度为 5, 首先先让绳子右端是 2, 然后 2-5 等于 - 3, 说明左端可以是有大于等于 - 3 的数,就找最近大于等于 - 3 的,发现就是 2, 所以 2 作为右端只会覆盖一个点
-
接着右端是 4,4-5 等于 - 1, 在左边找最近的大于等于 - 1 的,发现是 2, 所以可以覆盖两个点
-
接着右端是 8,8-5 等于 3, 在左边找最近的大于等于 3 的,发现是 4, 所以可以覆盖两个点
-
再有序数组中找最 (左 / 右) 位置的大于等于的可以用二分查找
-
我们遍历 N 个点,然后每个点做了二分,所以时间复杂度是 O (nlogn)
更好的解法:
滑动窗口
- Left 跟 Right
- Right 动,到时要保证窗口不要大于 L, 然后也要保证 R 位置的元素减去 Left 位置的元素不会超过 L
- R 可以走就继续走,不可以走就让 Left 位置走,so on…
时间复杂度就是 O (N)
# 小虎买苹果
普通解法:
- 首先让 N/8 获得最多能用几个乘 8 个的袋子,然后接着让 N-(N/8), 看看能不能让乘 6 个的袋子搞定
- 如果不行我们就减少乘 8 个的袋子,变成 N/8-1, 然后看剩下的让乘 6 个的袋子搞定
- so on…
- 到哪个行了我们直接返回
注意其实我们不需要一直让乘 8 个的袋子 - 1-1… 然后试剩下的行不行
- 我们只需要测到一个 point, 我们减去用乘 8 个的袋子的苹果数量,还剩下的需要让乘 6 个的袋子苹果数量如果超过了 LCM (6,8) 就可以直接返回找不到了,因为如果剩余的数正好是 LCM (6,8) 说明这个数既可以被 8 的倍数搞定也可以被 6 的倍数搞定,但是这里是超过了 LCM (6,8), 说明现在 6 只能搞定 LCM (6,8), 但是超出的部分肯定搞定不了,因为我们之前的尝试中,先让 8 尝试所以 8 一定会尝试然后让剩下的数让 6 处理,之所以 6 处理不了才会到这一步.
最优解:
打表法
- 如果输入输出都是 int, 可以直接弄一个很傻的结局方法然后接着拿很多个输入参数来测,打印每一个的输出,接着看输出看有什么规律,直接按照规律写代码
# 幂次方吃草
一般思路
public class Main {
public static String winner(int N) {
if (N <= 4)
return N == 0 || N == 2 ? "羊羊" : "牛牛"; //这些按照我们自己看的决定的答案
int eatTest = 1; //先从1份草开始试
while (eatTest <= N) {
if (winner(N - eatTest).equals("羊羊")) ..
return "牛牛";
eatTest *= 4;
}
return "羊羊";
}
}
老师代码:
打表代码
public static String win(int N){
return (N)%5==0||(N)%5==2?"羊羊":"牛牛";
}# 牛牛颜料
老师做法反过来了,就是 R 左边不能有 G
暴力解法:
-
我们分两个区域,一开始左边是空右边是数组 [0,…,s.length-1]
此时我们直接把右边区域所有的 G 变成 R
-
然后左边区域 ++ 变成数组 [0,1], 右边区域–变成数组 [1,…,s.length-1]
此时我们直接把左边区域所有的 G 变成 R
此时我们直接把右边区域所有的 R 变成 G
-
so on… 挨个试每次试都记录需要改变几个颜料,然后用一个变量存最小次数的就行了
…
-
然后左边区域 ++ 变成数组 [0,s.length-1], 右边区域–变成空
此时我们直接把左边区域所有的 R 变成 G
这样我们就暴力测出了所有让 R 左边不能有 G 的方法,期间我们用变量存下了那个改变颜料最小次数的数量,这个之后就是答案
时间复杂度为 O (N2)
优化解法:
申请辅助结构,把每次查询的东西生成好,这样之后每次查询就不需要遍历,直接查询拿到值就可以获取到想要的值就可以了
此时老师改过来了,G 左边不能有 R
- 首先遍历数组,看 0 到那个下标一共有几个 R
比如说:

- 有了这个数组之后,想要查询任何一个位置,0 到那个位置的 R 数量都可以给你,这样你就不要一个一个遍历重复的去找有几个等等等
- 我们可以同样从后面遍历,代表当前位置到 s.length-1 位置上一共有多少 G
比如说:

- 有了这个数组之后,想要查询任何一个位置,那个位置到 s.length-1 的 G 数量都可以给你,这样你就不要一个一个遍历重复的去找有几个等等等
因为我们在上面暴力做法,我们左边区域和区域都有元素时,我们同时需要左边到那个位置的 R 数量和右边到那个位置的 G 数量,我们可以从数组直接获取到那个数 (O (1)), 然后直接用,不需要遍历去找 (O (N)), 还可能是重复操作
# 矩阵最大正方形边长边框
对于任何一个 nxn 的矩阵
- 一共有 O (n4) 规模的长方形子矩阵,常数项很小,因为可能会有重复的
- 一共有 O (n3) 规模的正方形子矩阵,常数项很小,因为可能会有重复的
暴力解法:
优化解法:
预处理–> 想办法存一些信息关于检测是不是都是 1, 这样就不需要那四个 for 循环了,直接从存信息的里面取
- 生成一个矩阵跟原本矩阵一样大
- 这个新的矩阵 right,right 的每一个点存的是包括当前的点,以及他当前行右方的所有点, 一共有多少个连续的 1
如果我们从左边开始还是要遍历,为什么不直接从右边开始往左,有一个加一个,等等等这样就不需要遍历了
- 有了这个矩阵,之后我们接着再生成一个矩阵名为 down,down 的每一个点存的是包括当前的点,以及他当前列下方的所有点, 一共有多少个连续的 1
得出的方式跟 right 一样,注意此时我们需要一列一列的做,或者一行一行也可以,但一定是从下往上填 (跟 right 从右往左填同理)
- 有了这两个矩阵之后,比如说在我们选定了一个作为正方形左上角的点比如说 (4,5), 然后里面那个 for 关于边长的遍历到了 3
我们此时就可以:
原本需要四个 for 循环挨个遍历才能知道的事 (常数蛮大的 O (N)), 此时就是取数据变成了 O (1)
所以不用预处理方式 O (N4), 用来预处理 O (N3)
# 利用等概率实现另外一个等概率
第一个问题:
-
先让 f 等概率返回 1 到 5
- 如果是 1 或者 2, 设置为 0
- 如果是 3 或者 4, 设置为 1
- 如果是 5, 重新就算
这个实现了等概率返回 0 和 1 的函数
-
现在就想二进制, 三个二进制为代表 0 到 7 的数,我们可以用这个函数随机生成三个 0 或者 1 的数,这样就能做到 0 到 7 的数等概率,我们可以
- 如果结果是 0 到 6 就加 1, 这就做到了 1 到 7 等概率
- 如果结果是 7, 就重新做那三个二进制位的数
同样的问题,不同的数–> 只给等概率产生 13 到 21 的,生成等概率产出 30 到 59 的
- 先把 13 到 21 的函数做成产出等概率的 0 或者是 1
- 13-16 代表 0
- 17-20 代表 1
- 21 就重做不要 (这个不是必须的,要是总共偶数个,那其实直接就是 0 或者 1 等概率产出了)
- 30 到 59 等概率其实就是 0 到 29 等概率 (只不过最后加上 30)(这种题都这么想!)
- 看 0 到 29 需要几个二进制位 (5 个), 接着拿那个 0 到 1 的概率的产出 5 个二进制,如果这个产生的数字
- 是 0-29, 直接加上 30, 返回
- 大于 20, 重做,一直做到是 0-29 区间的
第三个问题:
- 直接让 p 函数运行两次
- 如果是 00, 重做
- 如果是 11, 重做
- 如果是 01 (得到这个的概率就是 p*(1-p)), 代表 0, 返回
- 如果是 10 (得到这个的概率就是 (1-p)*p), 代表 1, 返回
做到了 0 到 1 等概率
# 形成多少个二叉树结构
只说结构,不关心值
- 如果大于两个节点
- 一个头节点然后
- 没有左节点,N-1 个右节点
- 1 个左节点,N-2 个右节点
- 2 个左节点,N-3 个右节点
- …
- i 个左节点,N-i-1 个右节点 (可以说左树的每一种都是可以是跟右树的组合–>
f(i)*f(N-i-1)) - …
- N-1 个左节点,没有个右节点
- 所有可能的结果加一起就是方法数
# 完整括号字符串
先检查一个字符串是不是完整的
- 从左到右遍历括号字符串,有一个变量是 count
- 遇到左括号 count++, 遇到右括号 count–
- 如果在期间任何一个时候 count 变成小于 0 了,那直接代表这个不是完整的,因为我们是从左往右的,要是 count 期间任何时候变成负数了,就说明是走过的一块右括号更多,这肯定不完整
- 如果满足了上面一点,那么遍历完后,count 必须等于 0, 才能说明这个字符串是完整的
对于这个问题
- 我们同样像上面说的一样遍历等等等,再有一个变量叫 ans
- 如果期间遇到 count 是 - 1, 我们让 ans++, 代表我们填了一个括号让这个右括号有一个左括号,count 变回 0
- 遍历完的时候,我们 ans 存的就是此时需要添加的左括号,我们看遍历完的 count 如果不是 0 (比如说 5), 那就代表有 5 个多的左括号 (也就代表我们需要再添加 5 个左括号才行), 我们直接让 ans 此时的数加上 count 也就是我们需要添加的所有的括号数量.
# 去重数字对
- 把所有数放进 hashset 里面去重
- 然后 hashset 每一个数都去检查当前这个数加上差值的那个数在不在 hashset 里面 (注意!只看自己数加上那个差值的,不要也看减去的,会重复的!(只看一个就行))
- 如果在那就形成一对,如果不在就没有这一对,看 hashset 下一个元素
# magic 操作
解法:
业务问题需要看情况,分析各种情况,看些个 pattern 什么的,再加上小贪心
-
如果两个集合平均值一样,那不管从哪个集合拿哪个元素 (小于,等于,大于平均值的数) 都不会让两个集合的平均值增加
-
如果两个集合平均值一个大一个小
- 那不管从小的平均值集合拿哪个元素 (小于,等于,大于平均值的数) 到大的平均值集合都不会让两个集合的平均值增加
- 不过可以从大的平均值集合拿
小于自己平均值但是大于小的平均值的元素到小的平均值集合可以做到会让两个集合的平均值增加
-
不过要是大的平均值有多个
小于自己平均值但是大于小的平均值的元素该挑哪个?
我们选那个最小的符合的数, 小贪心,因为这个数是可以选的数中对于我们大的平均值的集合最大的拖后腿,所以把他移到更小平均值的集合可以最大幅度提升我们当前集合的平均值,以及让我们小的集合有最少的平均值的提升
- 这么做可以让更多在大平均的集合里面的元素符合条件 (可能原本不符合), 现在因为大平均的集合增长了很多,小平均的结合增长了但是没有那么多,那么可能现在更多元素是符合
小于自己平均值但是大于小的平均值的元素的条件了
时间复杂度就是 O (NlogN), 那个排序的操作
# 合法括号序列的深度
- 跟之前说道的,用 count, 在遍历期间 count 变成的最大值就是最大深度
# 最长合法括号子串
- 我们可以对于每一个括号字符都存一个对应的数,这个数代表当前字符作为结尾,最长的合法括号子串是什么
- 可以用 dp

- 如果是一个左括号,不可能作为结尾,所以直接把所有的左括号位置的在 dp 表中设置为 0’
- 对于一个右括号,如果他的下标是 i,dp [i] 的值可以靠 dp [i-1] 的值得到,比如说 dp [i-1] 是 4, 代表那个 i-1 位置的右括号作为结尾最长的合法括号子串长度是 4, 我们接着就需要 i-1-4 (那个 i-1 位置的右括号作为结尾最长的合法括号子串之前那个括号) 位置的括号,然后检查是不是左括号
- 如果是的话那么 dp [i] 的值起码是 6, 不是肯定是 6, 这是因为 i-1-4 位置 (假设我们叫他 p 位置) 考虑进来了,我们还需要 dp [p-1] 位置的值加到 6, 才是我们当前 dp [i] 的值 (只需要截这一块一次,不需要考虑什么 dp [p-1-dp [p-1] 位置的值] 的值,因为 dp [p-1] 的值就是最长的结论)
- 如果不是左括号,那么 dp [i] 的值肯定是 0
- dp 表中最大值就是答案,这个可以边设 dp 的时候边得,不需要都得出来之后又遍历什么的获取这个值
# 将一个栈里面的数据排序
- 比如说原始栈为 A, 辅助栈为 B
- 先从 A 弹出一个,放进 B 里面
- 再弹出一个
- 如果比 B 栈顶小,直接放到 B 栈顶
- 如果比 B 栈顶大,把 B 栈顶一个一个弹出来放到栈 A, 直到栈 B 为空或者遇到比当前数大的栈顶,我们才把这个数放到栈 B 栈顶
- 接着再从栈 A 弹出 (可能有上面栈 B 里面放回来的), 重复上面操作
- so on… 直到栈 A 为空
- 此时栈 B 就是从底到顶是从大到小的顺序,我们再从 B 一个一个弹出放到栈 A, 此时栈 A 就是从底到顶是从小到大的顺序
# 根节点到叶节点最大权值
# matrix 查找元素
列子:

做法:
从右上角开始找
如果一个数找到越界了 (发现需要走左边检查但是当前在第 0 列走不了_或者是_发现需要走下边检查但是当前在最后一行走不了), 还是没有,那就不存在
如果 matrix 是 n*m 大小
- 我们如果暴力解法就是 O (n*m)
- 我们如果上面这个解法就是 O (n+m)–> 最多走一行加一列
# matrix 找到含有最多 1 的那一行
每一行 0 肯定是会在 1 的左边,让你找到 matrix 里面含有最多 1 的那一行
列子:

这个列子,第 2,3 行数的 1 最多,所以返回 2,3
-
从右上角开始,把这个右上角所在的行数放进一个 list 里面去,一个变量 ans 为 0
-
如果左边有 1, 就一直走走到没有 1 的话就停,期间记录一共有几个 1 存到 ans
-
如果走完了,或者没有 1, 此时再往下
- 如果是 0 就不要记录 (我们之前存的已经目前来说是最好的)
- 如果是 1, 就看左边有没有 1
- 如果有就一直走走到没有 1 的话就停,期间让 ans++ 就行,这个明显更长所以直接把 list 里面的清空把自己放进去,然后 ans 也是存他这一行的 1 的有多少
- 如果没有 1, 代表当前的这一行跟之前的那一行长度一样,直接把当前行数存进 list (不要清空 list 什么的!)
继续往下走…
-
最后走完了,list 里面存的那个就是答案
比如说,另外一个列子

# 打包机器 (洗衣机问题)
解法:业务问题加贪心
-
如果知道一共有多少个衣服,然后有几个机器,我们就知道每一个机器应该是多少衣服
-
对于一个机器来说,我们可以得出他左边机器所有的衣服有多少 (也可以知道缺 / 多少), 然后也可以得出他右边机器所有的衣服有多少 (也可以知道缺 / 多少)
-
如果对于那一个机器来说
-
如果左右两边都是负 (指的是都缺衣服), 那么 ** 至少需要左边缺的数量 + 右边缺的数量这么多轮 **
-
如果左右两边都是正 (指的是都多衣服,需要往外抛), 那么 ** 至少需要 Math.max (左边多的数量,右边多的数量) 这么多轮,这是因为两边都可以同时往我们当前这个机器丢衣服 **
-
左右一个正一个负,那么 ** 至少需要 Math.max (左边多 / 缺绝对值,右边缺 / 多绝对值), 这是因为我们可以多的那一边给我们当前机器给衣服,同时我们这个机器把衣服给到缺衣服的那一边,一边结束了不代表另外一边也结束了,还要继续把衣服给当前机器或者从当前机器拿衣服 **
-
如果左边 / 右边没有机器,说明当前是在第一台或者最后一台机器,那就认为那一边没有多的或少的
-
-
我们可以对每一台机器都像上面操作,获取每一个机器对他来说至少要做出多少个操作存入数组 (或者变量保存最大值等等等)
-
其实答案就是数组最大值,那个最大值代表了那一台机器需要至少操作才可以,因为这个是最大值,代表所有的机器至少需要那些操作才能真正达到最后每一个机器都有同样的衣服
这里那个 leftSum 是边遍历边存上之前元素的累加和,也就是当前元素左边所有的元素的累加和
# zigzag 打印矩阵

- 两个位置一个 A 一个 B, 一开始在 (0,0), 打印
- 然后 A 的 col+1,B 的 row+1, 看现在这两个点形成的斜线,挨个按照你想要的顺序打印 (要么 A 打印到 B, 要么 B 打印到 A)
- 如果 A 无法再往右就往下,如果 B 无法再往下就往右,然后看新生成的斜线,挨个按照你想要的顺序打印 (要么 A 打印到 B, 要么 B 打印到 A)
# 螺旋打印矩阵
- 我们只关心两个位置,一个左上角,一个右下角,只需要让这个两个位置形成的这一圈按照正确顺序打印就行了
- 这个打印完让他们的斜位置成为新的左上角新的右下角,然后再管这个新形成的这一圈就行了

- 如果左上位置和右下位置错过去了 (行或者列错过去了), 就停止

上面停止不是因为到了同一个列,而是因为错开了,我们左上角的 row 比右下角的 row 要大,这就是错开了 (或者就是我们左上角的 column 比右下角的 column 要大)
如果我们没有错开,然后左上角位置和右下角位置在同一行 / 同一列 (甚至重叠), 都需要打印出来


# 矩阵中顺时针转动 90 度
跟上一题同理,先把外面一圈弄好,再弄里面的一圈,再弄那里面的一圈,so on…
- 对于每一圈,我们分组,我们先把四个角分为一组
- 然后左上角占右上角的位置
- 右上角占右下角的位置
- 右下角占左下角的位置
- 左下角占左上角的位置
- 然后再让那四个角往上 / 下 / 左 / 右 (就是同一个圈上的) 走一步,那四个元素,同样操作,so on…

分成的组数(一共有多少组)其实=当前圈右下角的col-当前圈左上角的col
# 拼接 sm
- 这个数可以被化解成他的质数因子的和,比如说 20=2*2*5
- 现在的问题就是以下哪个最优
- 我们先搞出两个然后再给这个 * 5 (也就是两个搞出五份来) 然后再 * 2 (也就是两个搞出五份来等于 10 个再搞出两份来), 还是
- 我们先搞出两个然后再给这个 * 2 (也就是两个搞出两份来) 然后再 * 5 (也就是两个搞出两份来等于 4 个再搞出五份来), 还是
- 我们先搞出五个然后再给这个 * 2 (也就是两个搞出两份来) 然后再 * 2 (也就是五个搞出两份来等于 10 个再搞出两份来)
所以,可以这么写,就是顺序不知道怎么样
我们还需要质数只能是用操作 2, 要是操作 1 的话好像是多了就不行了,永远就不会达到
https://www.bilibili.com/video/BV13g41157hK?p=22&spm_id_from=pageDriver [1:00:00 部分左右]
这样答案反正就是这些 质数因子加在一起-质数因子的数量
# 字符串数组找出现最多的前 k 个
- 用一个 map, 遍历字符串数组然后存每一个字符串以及出现的次数
- 接着把 map 里面东西按照每一个出现次数放进大根堆,之后 k 值有多少,你就取出多少就行
或者
- 用小根堆也可以,不过我们要确保小跟堆大小只有 k 个,必须加的元素要比此时小根堆的堆顶元素要大的时候才可以把堆顶 poll 了然后这个元素加进去 (让系统自己帮你调整现在的小根堆,或者自己弄的结构那么自己调整)
用小根堆的好处就是可以快速知道当前元素门槛有多低
而且事件复杂度是 O (k), 而不是像大根堆是 O (N)(N 是字符串类型有多少个不一样的字符串)
# 如何创建一个动态的结构,随时维持次数最多的前 k 个
需要一个数据结构,我们想要保存一个字符串次数最多的前 k 个,但是允许我们这个字符串次数随时都会变换,所以是很动态的.
就好比候选人选举,他们的得票一直是在变的,我们如何随时都可以获取到当前获票最多的前 k 个
两个方法:
- add 方法,加一个字符串
- printTopK 方法,打印前 k 个次数最多的字符串
这里我们就不能用原本的方式了,因为要是用户加了一个字符串,我们上面做法就是让 map 里面数据加加,然后对于所有数据再次做大根堆 / 小跟堆?这样肯定不行,很浪费时间!
我们希望上面两个方法代价不高
解法:
要我们手动写一个堆结构,不能用系统给的堆结构,因为无法对系统堆结构已经加到里面的元素进行更改等等等,就算要改的话他也是扫描全局找到那个被改的然后才能改,代价很高,但是我们自己的结构可以知道哪个被改了,然后对于那个做 heapify/heap insert 操作修正那个堆
注意我们假设如果出现次数一样的字符串选谁都可以,比如说十个字符串出现三次而且都是出现最多次的,而我们只需要打印前 5 个,那这 10 个里面随便 5 个都行的话就可以用这个方法
-
一个 hashmap 用来存字符串以及出现次数,一个按出现次数统计的小根堆 (以及 heapSize 代表大小,比如说这个例子里面大小为 3), 一个 hashmap 用来存一个字符串和他在堆上的位置 (指针)–> 如果字符串没在堆上,要么那个字符串不在这个 hashmap 里面,要么存的对应的位置为 - 1
-
当加一个字符串时,就检查在不在第一个 hashmap 里面
-
如果没在就加进去,然后检查此时堆有没有满 (一开始是空的), 没满就放进堆里面,然后把当前字符串和对应堆上的位置存到堆位置 hashmap 里面去
-
如果在就更新 hashmap 里面出现次数,然后看这个数在不在堆里面,如果在就做从 0 位置开始做 heapify (考虑这次这个数的增加了), 当然,堆里面位置换了,堆 map 也要更新所有元素在堆里面换成的新位置
-
如果这个加的字符串不在 hashmap 里面,然后堆当然也没有,此时堆也满了,就看能不能干过堆顶,干不过就只是把他记录到堆位置 hashmap 然后它对应的位置为 - 1
-
如果这个加的字符串已经 hashmap 里面,就更新值,然后发现堆满了而且这个字符串没在堆上,就拿当前这个更新后的值跟堆顶比较,如果更大加把堆顶去掉把这个放进去,做 heapify, 此时这个原本的堆顶在堆位置 map 更新他位置为 - 1, 然后其他的元素因为做了 heapify 都需要检查一下看一下有没有变换位置更换到正确位置
-
那个 index 指的是 heapSize, 之后换名了换成 heapSize
swap 的时候注意把堆位置里面数据改变!
打印直接打印堆里面的数据就行了
这个堆位置的 hashmap 其实就是快速确认一个字符串在不在堆上用的,如果不在就是 - 1, 如果在就可以快速查出来他的位置,查出来他的位置要是这个是更新了,比如说加了一定的值,就可以对他做 heapify/heap insert 操作,维持堆结构,这也就是为什么我们使用自定义的堆结构
# 栈最小值
- 一个 data 栈用来存数据,一个 min 栈存最小值
- 当一个数据进来,我们把 data 栈中此时最小的值压入 min 栈中 (可以重复压入,这是为了之后 data 栈出栈,我们的 min 栈也会跟着出栈,保留此时最小值)
弹出的时候两个栈同步弹出就行了!!!min 栈保留的栈顶一定是当前 data 栈里面所有数据最小的
# 用队列实现栈结构以及用栈实现队列结构
# 用栈实现队列
- 两个栈,一个叫 push 栈,一个叫 pop 栈
两个原则
- push 栈要是倒东西 (pop), 需要一次倒完
- pop 栈如果已经有东西,push 栈一定不要往里面倒数据,只有没数据的时候我们才可以让 push 栈里面数据一下全部倒完倒到 pop 栈里面去
- 我们把用户传进来的数据都压在 push 栈

- 如果想弹出的时候只需要把 push 栈一个一个弹出放入到 pop 栈里面去就行了

可以发现很多方法都会尝试看能不能把数据从 push 栈倒到 pop 栈备用,因为我们取数据毕竟都是从 pop 栈取数据,但是加数据是加到 push 栈里面去,所以有时我们数据都在 push 栈不在 pop 栈,也有可能 pop 栈有数据,所以我们需要 pop 数据都被取完了我们 push 栈数据才能进,* 而不是直接加进去,因为顺序会被打乱!!!*
# 队列实现栈
- 两个队列结构 A 和 B
- 用户放数据都放到队列 A 里面去

- 当用户想要取数据,我们把队列 A 里面除了最后一个数据的数据全都按顺序放到队列 B, 此时队列 A 有的数据就是如果用栈的话,可以获得的栈顶数据,就把那个数据弹出

- 此时队列 B 就相当于是我们的之前的 A, 要是相加数据直接往栈 B 加,如果想取就把除了最后一个元素其他所有的元素都放进队列 A 里面去,此时队列 B 有的数据就是如果用栈的话,可以获得的栈顶数据,就把那个数据弹出

太绝太绝 绝绝子
# 动态规划的空间压缩技巧
- 比如说一个 dp 表二维的,我们只想要一个格子的值作为答案,我们可能只需要一个数组就能做到得出答案
- 比如说:

f 依赖 a 所以可以得出 f 换掉 a 的位置,g 依赖 f 和 b (我们此时都有) 所以可以得出 g 换掉 b 的位置,so on…
一个一个边,然后一行一行边,最后变成最后一行,我们就有对应的答案的格子
空间从 2 维变成 1 维,省空间的做法,时间还是一样的
注意!!!我们具体该从哪一行开始,从左到右还是从右到左,以及各种具体的操作都是要看你具体的 dp 每一个格子是怎么依赖的,我们还可以使用变量等用来记住之前一行中可能会需要用到的值
就是比如说我们有 4*100 万的数组,我们可以设置为每一列作为我们数组大小,然后进行 100 万次,不过具体的还是需要看怎么依赖等等
甚至不需要是同一行同一列的,我们只看依赖的顺序,先把先被依赖的加进去,然后按照别的对这些依赖一个一个更新…
甚至三维等等等都可以压缩成二维…
# 装水
- 跟洗衣机问题很像,我们只关心每个位置自己上方可以留下多少水
举列:当前 i 位置是 5, 左边最大值 10, 右边最大值 20
-
那么当前位置肯定会停 5 个水,因为超过 10 的话肯定都会从左边溜走了
-
所以我们需要
Math.min(数组0到i-1位置最大值,数组i+1到结尾位置最大值)-nums[i]这个就是对于当前数来说是至少能装的水- 如果这个结果负数,那么当前数就是 0, 能存 0 个水
所以最终是
Math.max(Math.min(数组0到i-1位置最大值,数组i+1到结尾位置最大值)-nums[i],0) -
所以只要给每一个位置的都算出这个,让他们加一起就是答案
-
时间复杂度 O (n)
你可能会想用两个辅助数组分别存每一个位置他左边到他的最大值,以及他到他右边的最大值
但是我们甚至可以想一个不用这两个辅助数组,空间复杂度 O (1) 也可以,时间复杂度还是 O (n)
列子:

- 首先一个变量 all 一开始 0,leftSum 代表左边我们遍历过的最大值,rightSum 代表右边我们遍历过的最大值,一个 left 变量一个 right 变量
- 0 位置和 8 位置自己肯定留不下水,因为有一边是没高度的,水一定会流走,所以都不看. leftSum=10,rightSum=7,left 指向 1 开始的位置,right 指向 7 结束的位置
-
此时我们其实可以直接让 R 位置的结算获取最大值,因为就算我们 leftSum 并不是对于他来说是最大值,但是 rightSum 就是对于他来说是右边的最大值而且这个已经比 leftSum 要小了,我们需要的就是那个更小的那个,所以,可以直接获取 R 位置的水量也就是 7-3 等于 4 (存进 all 变量去), 然后 R–
-
然后 R 就是 6 位置的 11 了,此时我们也可以对这个位置结算水的数量,也就是 0 (因为 7-11 等于负数), 然后 R–, 注意这个比此时这个 rightSum 要大,所以 rightSum=11
-
然后接下来 L 位置的可以结算了,因为此时对于他来说 leftSum 就是他左边的最大值,然后这个比 rightSum 要小,虽然这个 rightSum 并不一定对于这个位置来说是他右边的最大值 (其实确实不是,他右边 12 才是最大值) 但是我们的 leftSum 已经比 rightSum 要小了,所以可以直接用 leftSum 算就行了,也就是 10-8 等于 2,L++, 然后 8 并没有比此时 leftSum 的 10 大,所以不更新 leftSum 的值
-
就是这样就是检查此时 rightSum 跟 leftSum 哪个更小
- leftSum 更小,那就用 leftSum 获取 L 位置的水 (存进 all 变量里面去), 然后 L++, 检查 L 位置的元素是不是比 leftSum 更大,更大的话要更新
- rightSum 更小,那就用 rightSum 获取 R 位置的水 (存进 all 变量里面去), 然后 R–, 检查 R 位置的元素是不是比 rightSum 更大,更大的话要更新
-
之后所有元素都结束之后 (L>R 的时候), 我们 all 变量存的就是答案
O (n) 时间复杂度,O (1) 空间复杂度
# 砍数组,最大的左右部分的最大值的差值
-
首先找到这个数组的全局最大值
-
要是这个最大值是在左部分,那他就是左部分的 max, 接下来就是决定该怎么划分可以让右部分的最大值尽量小,我们知道右边部分肯定会包含 n-1 位置的数,让他最大值最小的方式就是让他只包含 n-1 位置的数即可–> 所以就是
全局最大值-arr[n-1]你可能会想,不对啊,要是我门比如说 n-2 位置的数比 n-1 位置的数要小,那不就代表我们可以获得绝对值差值更大的吗
但是我们要的是左右部分最大值,要是 n-2 位置的数比 n-1 位置的数要小,那么最大值还是选的 n-1 位置的数
你可能会想,那要是 n-2 位置的数比 n-1 位置的数要大,那就可以让有部分最大值是这个数了吗
但是我们为什么要这么做,我们想要差值最大的,你这给了个更大的数,岂不是让我们差值更小了吗
我们这个情况只包含 n-1 位置是有部分不管多长, 肯定是包含 n-1 位置的,然后我们看上面就知道只是包含 n-1 位置的右部分才是最符合我们想要的数,下面关于全局最大在左部分也是同理.
-
要是这个最大值是在右部分,那他就是右部分的 max, 接下来就是决定该怎么划分可以让左部分的最大值尽量小,我们知道左边部分肯定会包含 0 位置的数,让他最大值最小的方式就是让他只包含 0 位置的数即可–> 所以就是
全局最大值-arr[0] -
所以答案就是
Math.max(全局最大值-arr[n-1],全局最大值-arr[0])
-
# 旋转字符串
- 判断两个长度是不是一样,不一样直接返回
- 只有长度一样,那么我们让 a 变成 a+a (就是他自己两个字符串相连), 然后只需要看 b 是不是这个新 a 的子串就行了 (KMP 算法)

这个新 a 任意长度为 b.length (这个列子里面为 5) 的子串都是原来字符串的旋转词
所以要是 b 是这个的子串就代表 b 是原来 a 的旋转词嘛
# 咖啡问题
- 有个小根堆,存的是每一个咖啡机的时间单位以及在什么时候可用,排序是两个数相加谁小谁排在上面,所以堆顶就是所有机器谁现在泡完结束时间小的排在上面
- 对于每一个人都从堆顶拿一个,然后让第一个数加上第二个数 (结果就是这个人可以喝咖啡机的时间), 再把更新了第一个数的整体放回小根堆,下一个人…
-
这么做我们就可以获得对于每一个人来说什么时候可以得到咖啡 (以及喝掉) 的时候,也就代表我们可以获取到所有时间点有需要洗的需求了, 所以现在问题就是我们有一堆需要洗杯子的时间点,我们该怎么洗才能最快最短的让这些都洗完
我们有两种选择
- 洗咖啡杯的机器洗
- 自动挥发
-
所以这个就是个从左到右尝试的模型
可以改动态规划
# 相乘为 4
-
首先遍历,看有几个 (a 个) 奇数,有几个偶数但是只有一个 2 因子 (b 个), 以及有几个偶数但是包含 4 因子的数 (c 个)
-
如果 b==0
- 我们可以这么摆 奇 4 奇 4 奇 4… 这样交叉着摆就是最可以确保任何两个相邻的数相乘都会是 4 的倍数
- 如果奇数为 0 a==0 说明只有包含 4 因子的偶数,那么随便摆
- 所以奇数只有一个的时候 a==1 我们有 4 因子的偶数至少需要有 1 个及以上便足够 c>=1 (如果没有的话就返回 false)
- 如果奇数大于 1 的时候 a>1 我们至少需要每两个奇数之间都要有一个 4 因子的偶数 c>=a-1 (如果没有这么多的话就返回 false)
-
如果 b!=0
- 我们可以把所有这些只有一个 2 因子的偶数都放在一起,这样他们之间互相任意两个都可以相乘然后变成 4 的倍数
- 如果奇数是 0 a==0 我们把所有只有一个 2 因子的偶数都放在一起,然后剩下的都是有一个 4 因子的偶数随便放甚至没有都行 c>=0
- 如果奇数是 1 a==1 我们把所有只有一个 2 因子的偶数都放在一起,然后紧跟着必须是一个有一个 4 因子的偶数然后才能是奇数 (2222222…4 奇 (4)) c>=1
- 如果奇数大于 1 a>1 我们把所有只有一个 2 因子的偶数都放在一起,然后紧跟着必须是一个有一个 4 因子的偶数然后才能是奇数 (2222222…4 奇 4 奇 4…) c>=a
所以同一化简为 c 要 >=a 即可,如果不符合,那么直接返回 false
还有就是 edge case, 比如说只有一个 2 因子的数,那就必须需要一个 4 因子的数一块才行
这种题就是分类,然后对于每一种可能就想需要什么,什么要求等等等,然后看看符不符合要求,不符合直接返回 false
# 递归式从 O (N) 简化成 O (logn) 的方法
https://www.bilibili.com/video/BV13g41157hK?p=24
从头开始,数学有点差… 比较懵逼
要求是严格递归才可以!!!
如果你递归函数里面处了 base case 有什么 if (目前什么情况) 回调自己传某种参数 else 回调自己传另外一种参数
这样的递归函数不是严格递归的,他是按照你某个数据实际情况的,这种不行
严格递归就需要像 fibonacci 这种,比如说 f (n)=f (n-1)+f (n-2) 这种, f(n-1)+f(n+2) 这部分对于所有层都是固定的,那就是严格函数,所以就算是 f (n)=2f (n-1)+3f (n-2)-1000f (n-3)+0f (n-4)-200f (n-5) 这种,只要右边对于每一层都是一样的那么就没问题,还是严格地故意,可以用这个简化的方法

我们可以算出 a,b,c,d 的值
然后就可以用这些值算之后想要的值,就更快了
# 斐波那契数列快速幂解
暴力解复杂度为
O(2^N)
快速求 10^75.
75 转为 2 进制 1001011
int res=0;
intemp=10
t 每次和自己相乘,10^1 10^2. 10^4. 10^8. 10^16……
然后判断对应二进制位是否为 1 ,如果为 1 ,res= res * t
对于矩阵,每次也是 M^1 M^2 ……
对应二进制位为 1 乘进 res 中
# 剑指 Offer 10- I. 斐波那契数列
class Solution {
public int fib(int n) {
if(n==0)return 0;
if(n==1||n==2)return 1;
int[][]base={
{1,1},
{1,0}
};
int [][] res = matrixPower(base,n-1);
return res[0][0];
}
public int[][]matrixPower(int [][] m, int temp){
int[][] ret = {{1, 0}, {0, 1}};
while(temp!=0){
// 如果对应二进制位为1 则乘进去
if((temp&1)!=0){
ret = muliMatrix(ret, m);
}
m = muliMatrix(m, m);
temp>>=1;
}
return ret;
}
public static int[][] muliMatrix(int[][] a, int[][] b) {
int[][] c = new int[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % 1000000007);
}
}
return c;
}
}
# 值得记忆
//当二进制不为0时
while(temp!=0){
// 如果对应二进制位为1 则乘进去
if((temp&1)!=0){
ret = muliMatrix(ret, m);
}
//如果二进制位为0,则自乘
m = muliMatrix(m, m);
// 右移
temp>>=1;
}# 背包问题的变种
- dp [i][j],i 为体积数组中哪一个下标,j 为 0 到 w 的体积
- 所以这个 dp 最后一行 (我们这里是从上往下方式,也就是从下往上依赖), 最后的累加就是答案
# 牛牛找工作
- 用有序表,难度小的排在前面,难度一样的话报酬更高的排前面
- 然后对于每一组难度一样的,只留下报酬高的,让报酬低的走开
- 然后现在看哪个难度增加了但是报酬没有增加的直接走开,剩下的保留

现在我们就创造了难度递增并且报酬也是递增的有序表
接下来对于每一个小伙伴,就选对于他能力来说最高能接受的难度的工作,其实那个就是对于他来说是报酬最高的
# 符合人们日常书写
比如说,一般都是 7, 而不是 07, 等等等
所以,三点
- 数字之外只能有减号
- 如果有减号,必须是在开头,必须是一次,必须之后必须是数字,而且那个数字不能是 0
- 如果开头第一个是 0, 后面必须没有数字
如果可以转的话,我们就可以:
不管原来是不是负数,我们都用一个负数来接收答案
这是因为:负数的表达值范围比正数的表达值范围大一个
要是我们接收的数字是 - 2147483647, 那么用我们用正数接收,那么就会越界
虽然接收正数的最大值没关系,但是接收负数的最大值会多一个接收不了,所以干脆都用负数接收 (就是一个一个接收), 然后接收完再看要是负数直接就返回,如果是正数那么就变成正数返回
# 目录显示
使用前缀树
- 组织成一个前缀树 (先建立一个空节点,然后遍历字符创建前缀树)
- 深度优先遍历解决
- 第一层的直接打印
- 第二层的打印两个空格然后打印那个字符
- 第四层的打印四个空格然后打印那个字符
- 这里可以看出每一个节点本身还把那个字符存上了,其实不用,一般都是存在那个 nextMap 属性就行了
- 还有那个 nextMap 是有序表,这是因为你想排序那些字符的比如说 a/b 和 a/c, 用有序表就可以先打印 a 下面的 b 然后才是那个 a 下面的 c (属于同一个头层) 的所有同一级的所有按照顺序排
# 二叉树变成双向链表
二叉树 dp 递归套路
-
对于我们二叉树一个节点 x 来说,我们只需要他左树和右树头节点和尾节点,这样我们可以
- x.last (left)= 左树尾节点
- 左树尾节点.next (right)=x
- x.next (right)= 右树头节点
- 右树头节点.last (left)=x
返回以 x 代表的整颗树的尾节点也就是搜索二叉树最左的节点 (最小值的那个) 和 x 代表的整颗树的头节点也就是搜索二叉树最右的节点 (最大值的那个)
最后答案就是整个的树的头节点 (start), 也就是整个树最小的值的那个节点
# 在一个二叉树中找最大搜索二叉树的节点个数
子树就是选定一个头节点之后,下面所有节点都包括才算子树
左右树都需要
- 最大搜索子树的头节点
- isBST
- 最小值
- 最大值
- 最大搜索树的节点个数
然后就是看当前节点和他的左右在一起是不是 bst, 如果是就要设置 isBST 然后设置最大搜索子树的头节点以及最大搜索树的节点个数的值
# 招聘信息和打分系统
就是找连续子数组最大值的和
# 整形矩阵的子矩阵最大累加和
列子:
方法:
- 在 0 到 0 行上,哪个子矩阵累加和是最大的
- 在 0 到 1 行上,哪个子矩阵累加和是最大的
- 在 0 到 2 行上,哪个子矩阵累加和是最大的
- 在 1 到 1 行上,哪个子矩阵累加和是最大的
- 在 1 到 2 行上,哪个子矩阵累加和是最大的
- 在 2 到 2 行上,哪个子矩阵累加和是最大的
如果还有其他行就各种等等等…
然后对于上面说的每一个,比如说 0 到 0 行,我们就可以用上面说的方式直接找到对于 0 到 0 的答案
但是如果是 0 到 1, 我们需要让 0 行跟 1 行每一列的数字跟同列数字相加,然后再对结果做上面说的一个数组找出最大的,找出的 max 就是 0 到 1 行对应的子矩阵最大累加和
压缩数组技巧
时间复杂度: O (N2*M)
# 路灯问题
也可以遍历那个字符串,对于每一块为.(路) 的区域计算有多少.(路), 然后对于每一块除 3 向上取整
或者如果我们在 i 位置
- 如果 i 位置是 X (墙), 那就不给灯跳到下一个
- 如果 i 位置是.(路), 那就看 i+1 位置的,如果
- i+1 位置是 X (墙), 那就把灯给到 i 位置的
- i+1 位置是.(路), 那就把灯给到 i+1 位置的 —> 贪心
# 二叉树前序数组和中序数组找后序数组
- 一开始先序遍历第一个一定是后序遍历最后一个
- 然后在中序数组找到那个元素,此时中序数组左边的所有就是对于这个元素来说整个的左树
- 这个找到的区域前序数组也可以找到对应的,后序也会有
- 反正想法就是对于每一个区域来说找到一定区域的答案,然后递归等等等
可以用 hashmap 做预处理,就不用每次遍历去找中序数组那个元素所在位置了
复杂度就是 O (N), 数组每一个元素都只经过一次
# 数字打印出成中文的样子
英文版本:
从小范围扩到大范围的问题
# 完全二叉树的节点个数
- 遍历到左树最底层获取层数,然后看头节点的最左最低节点层数跟我们的左树一不一样
- 如果一样,那么左树就是满的,可以获得左树的节点个数然后看右节点开始的右树看有多少个…
- 如果不一样,那么右树肯定是比左树少一层且满的,可以获得右树的节点个数然后看左节点开始的左树看有多少个…
时间复杂度为 O (h2), 相当于对于一个高度的每一个节点都需要过一次高度
- 头节点需要过 h-1 个节点
- 头的左 / 右节点需要过 h-2 个节点
- 头的左 / 右节点的左 / 右节点需要过 h-3 个节点
- …
这个算法也可以说是 O ((logN)2)
# 最长递增的子序列
O(N2) 答案:
- 有一个 dp 数组存每一个 arr [i] 结尾的递增子序列的最长长度
- 然后遍历原数组,对于每一个数组就去遍历左边找比他小的,然后如果有多个比他小的,就用那个比他小的且 dp 数组里面长度比其他比他小的还要大的那个,然后这个元素对应下标位置的 dp 元素就是那个比他小的 dp 数组中的值 + 1
- 最后遍历完,dp 数组最大的就是答案
O (NlogN) 答案:
- dp 加上 binary search, 参考上面 leetcode98 题
# 神器的数列
三种方式
- 获取到那个整个数,然后模 3
- 把每一位数字视为一个数相加然后结果模 3
- 1+2+3+… 一直加到那个 n 值的结果模 3 也可以!
# 找到 1-n 未出现整数
一定会有终止的时候,因为上面数字就是 1 到 N 之间
# 土豪女主播
你可能会想出这么一个递归:
但是上面这个没法结束,因为:

主要是那个减 2, 可能回到之前已经试过的
我们可以多加 basecase, 来确保返回
这么考虑 base case, 可以想对于这个业务的可能性,
一般想偶数奇数等等等可能性很不错
- 一开始的数是偶数,end 也是偶数,所以我们要是使用 + 2 的方式,就一直加 2 加 2 加 2… 是肯定能到的,我们可以先算出来这种方式一共需要多少个币,这个平凡解就可以作为我们的 base case, 因为我们想要的是币最少的方式,所以要是另外方法要是比这个平凡解要高我们也不需要,basecase 直接返回,而要是这个是比我们的平凡解要低,就需要
- 这样我们就可以人为的加 base case (限制), 来确保递归可以退出
然后对于我们这个问题还可以有针对于这个问题的限制,比如说
- 我们一开始 6, 结束值是 10, 我们不需要两倍于结束值,因为没必要啊,我们只需要 2*6-2 就行了,对于所有列子来说我们都不需要把当前数变成结束值的两倍然后慢慢 - 2 变成结束值
- 这个比较针对于问题,主要看你问题然后想出有什么限制等等等
最终答案:
# CC 直播运营
可以从结尾开始
- 从结尾节点开始,每一个节点都有一个 map (有序表) 来存 key 作为目前节点到结尾节点一共几天以及 value 是钱数
- 结尾节点之后,再做任何有 arc 指向结尾节点的节点,更新他们对应的各自的 map 的 key 和 value
- 每一个节点的 map 里面可能有多个记录比如说这个节点有多个 outgoing edges to other edges, 都要把对应的存上,注意我们还想要确保 map 里面存的 key 要是更大,那么 value 就一定更大,不符合的都删掉,然后接着去找下一个节点…
- 之后把每个节点的 map 的每个记录放到一个大 map 里面去,确保 map 里面存的 key 要是更大,那么 value 就一定更大,不符合的都删掉,之后这个 map 就可以查到任何一个天数内获得的最大收益
如果一个一节的 map 只有很垃的,请不要删,还是留着,因为:
后面连着的说不定有很好的
所以每一个节点都要保持一个 map, 而不是同用一个 map, 可能会提前把最符合答案得必须需要的一个节点的信息给清掉了
# 逻辑决定布尔值
- 假设每一个符号都是他是最后结算的
- 如果这个符号是 & 然后想要 True, 所以如果左边一共 a 种方法获得 true 右边有 b 种获得 true, 那么这整个就可以有 a*b 种方法是 true
- 等等…
可以改 dp (也就是两个二维表,一个 desired 是为 true 的一个是 desired 为 false 的)
# 最长不重复子串
对于一个 i 位置的来说,有两个瓶颈
- i-1 位置的推出来的那个最长没有重复子串的长度
- 之前的根自己一样字符的位置 + 1 到自己的长度
这两个哪个离当前 i 位置的元素最近,我们就用哪个
# 编辑距离
https://www.bilibili.com/video/BV13g41157hK?p=27&spm_id_from=pageDriver 1:38:00 处
# 删掉字符获得最小最小字典序的字符串
- 创造每一个字符的词频表 (出现几次)
- 然后再遍历,每遍历一个都让对应字符词频 - 1, 直到有一个字符词频为 0
- 此时我们遍历过的这一块就代表我们这一块区域的右边不再有那个词频变成 0 的字符了,所以我们必须在这一块挑选一个字符才可以最后让每种字符都有
- 我们选这一块区域的最小词频的字符,然后让那个选中的字符的左边去掉,然后右边去重新每一个去找各自的词频
- 每一次挑选一个字符,之后把这些字符拼在一起就是答案
https://www.bilibili.com/video/BV13g41157hK?p=27&spm_id_from=pageDriver 2:01:14 处
复杂度 O (k*N),k 为不同字符的个数
# 子序列
需要两个函数 g 和 f
- g 函数
- f 函数
# 排序后的相邻两数最大差值
- 如果 n 个数我们就准备 n+1 个桶,堆数组里面的数字划分到每一个桶里面去
- 最左边和最右边的桶一定会有元素装着最小和最大的元素
- 我们肯定会有空桶,所以答案就是不同桶之间的最大值 - 最小值就是答案,不可能发生在一个桶里面
- 所以我们每个桶其实可以用数组存,两个数组分别存每个桶的最小值和每个桶的最大值,之后只要算每个桶的最小值 (除了第一个桶) 和他之前有数的桶的最大值里面最大的那个差值就是答案
其实加的那个桶 (N+1 个桶,而不是 N 个桶是因为) 就是相当于加了个平凡解,加了这个就直接排除掉所有答案会在一个同一个桶内的可能性,从而排除掉很多不可能的可能性所以直接优化很多
可能性的取舍
# 区分数组获取区间数字的 xor 都等于 0
子数组问题,先想每个位置结尾的情况下怎么怎么样
我们看可以用 dp 数组,我们 dp [i] 代表 0 到 i 位置这一块最多能有几个区域 xor 为 0, 后面的都不管
从左到右,如果 i 位置
- 不是最优划分的情况下属于异或为 0 的区域的最后一个元素,就比如说现在是 1234, 然后 i 位置的是 4, 那这个就不是,以为它本身就是自己 4, 本身不是异或为 0 的区域。这个情况的话,其实有这个元素没有这个元素都一样,直接取 dp [i-1] 的值就行了
- 是最优划分的情况下属于异或为 0 的区域的最后一个元素
- 使用一个 map 记录每一个前缀 xor 和以及对应的最近的下标,这个用来快速找到当前 i 位置作为一个区域的最后一个位置的这个区域的第一个下标
我们这里要使用假设答案法
# m 面值的硬币的拼成的方法
- 可以想象是两个数组一个数组是所有普通币另外一个纪念币,然后一个 m
- 比如说 m 是 10, 那么我们需要知道多少种方法让
- 普通币拼成 0 的方法总数,纪念币拼成 10 的方法总数,他们相乘
- 普通币拼成 1 的方法总数,纪念币拼成 9 的方法总数,他们相乘
- 普通币拼成 2 的方法总数,纪念币拼成 8 的方法总数,他们相乘
- …
- 普通币拼成 10 的方法总数,纪念币拼成 0 的方法总数,他们相乘
- 最后把所有结果相加就是答案
其实就是两个 dp 二维数组
第一个对于任意枚
如果那个数组有三个元素,我们 m 是 10 的话,我们想要有一个 3x11 的二位数组
dp [i][j] 代表从 0 到 i 在数组里面位置的元素随便用凑到这个 j 这个数
一开始我们可以对于 dp [0/1/2][0] 都初始化为 1, 因为所有货币想要凑到 0 块钱就是不用当前货币就是 0 种方法
然后 dp [0][allcolumns] 可以做简单的数学填充好
之后下面的 rows 他的值是
dp[i][j]=dp[i-1][j](当前i位置的币一个不用拼成j)+dp[i-1][j-arr[i]*k](当前i位置的币用k个(k>=0,所以可能会是0,1,2,3,...), 剩下的值让 0 到 i-1 位置的处理,当然和这个j-arr[i]*k要 >=0)因为 k 可以是 0, 所以可以直接简化为:
当然别忘了,可以做优化!!!
每次有枚举行为,我们可以通过观察看哪些地方有重复的,想办法取消重复的
第二个对于只能使用一枚的硬币更简单,压根没有枚举行为,直接用或者不用就行了
用了这个两个 dp 表,用他们的最后一个 row 按照上面拼答案就可以了
# 两个数组找最大
这里老师再找第 k 小的数字
使用 binary search (不是最优解) (这个好像要是有重复数字就不对了)
- 一个数组里面做二分,之后一个数,然后拿这个数去另外一个数组里面去找二分看对不对,如果不对接着做二分,然后再另外一个数组找…
- 如果上面没找到,就反过来,在另外一个数组做二分找一个数,然后去之前那个找…
logN*logM时间复杂度
最优解
- 首先要找到上中位数 (比如说数组长度为 8, 上中位数就是 3 位置的数)
如果两个数组都是偶数个
那么如果 A 的上中位数 ==B 的上中位数,那么直接返回,那个就是他们在一起的上中位数
如果不等,那么就对于 这两个部分递归找各自的中上位数进行比较…
子问题的上中位数就是总问题的上中位数
如果都是奇数个
也是比较中上位数,如果一样直接返回
如果不一样:
https://www.bilibili.com/video/BV13g41157hK?p=31&spm_id_from=pageDriver 开头看之后的
# 摩天大楼
无非就是把数据归整成一个对象,然后把他们放进两个有序表,一个有序表代表存着当前最高高度以及出现几次,另外一个表靠着刚才这个表来算出当前点以及他对应的最高位置是什么.
目的就是为了找出每一个点和他对应的此时最高高度是多少,有了这个之后
# 累加和为 k 的最长子数组长度
滑动窗口,L 和 R
其实就是单调性,看一个数组从哪个开头可以不用试
不过要是这个数组要是有 0 有负数怎么办???
先遍历数组,弄一个前缀和数组,然后创建一个 map 保存前缀和与坐标,有相同前缀和只保存最前面那个。定义 max 保存长度,然后再遍历前缀和数组,每个前缀和元素减去 k,
如果这个有正有 0 有负的的数组累加和小于或者等于 k 的最长数组长度怎么办???
这个需要我们之前说过的,可能性的取舍,把不可能的排除掉,(用桶的那个方式)
两个数组,第一个数组代表从 i 位置到结尾所能形成的最小的累加和,另外一个数组对应着每一个 i 位置到结尾所能形成的最小的累加和结束的右边界。让我们相当于让数组变成很多很多的子数组,然后我们可以按照每一个子数组进行操作看看相加有没有大于 k, 没有就继续加直到加到超过了 k (更新答案).
但是精髓还不是这里,这样我们任意形成 O (N2) 的解法,因为可能 0 位置开始一直扩扩扩,发现不行就要从 1 位置开始一直扩扩扩,… 是不是可以优化!!!我们可以使用窗口,窗口不回退,比如说 0 位置开始不对,我们可以一直保持一个 sum, 然后可以直接 sum-arr [0], 就相当于从 1 位置开始继续了,然后继续测之前测到的右边界后面的…
这么做代表我们只关心我们可不可以让窗口边的更长,而不是当前位置开头到底对不对
# 铜板问题
Nim 博弈问题
把所有数字异或起来,如果非 0 那么先手赢,如果是 0 后手赢
如果一开始异或不是 0, 那么先手就会每一步都让结果变成异或为 0 让后手操作,这样后手怎么拿都会让结果不再是 0, 那么就相当于是最后先手胜利
如果一开始异或是 0, 那么此时这个先手就相当于是之前的后手了
# 伪进制
使用 26__伪__进制可以解决问题
# 蛇蛇
就是尝试!!!
因为不一定是到头,而是每一个点都有可能,所以要在外层 double for
然后在定义好那个方法就行,回调,把需要的信息组织好就行了
很喜欢这种想法,我们只关心获取到,然后之后不停更新我们需要的数据,之后直接用就行,而不是担心获取然后用等等等
改动态规划 (记忆法)
然后之后的…(省略掉,跟上面一样)
# dp 的空间压缩技巧
dp [i][j],i 是第一个字符串的所有字符,j 是第二个字符串的所有字符
dp [i][j] 代表第一个字符串 i 位置的字符结尾并且第二个字符串 j 位置的字符结尾情况下,最长的公共子串是多长, 并且这个最长公共子串也必须要以这个第一字符串的 i 位置的字符以及第二字符串的 j 位置的字符结尾
可以直接算出:
其他的相等的其实就是他左上角的值 + 1
(上方图有些细节是填错的)
最后答案就是整张表的最大值
但是真的需要表吗,其实用几个变量也可以达到同样的效果,这个表只存在脑海里,我们可以从左上角,一个一个算出来,每个点都依赖与他的左上角,同时记录出现过的最大值
# 两个字符串最长公共子序列
跟上面一样也是二维表,dp [i][j] 代表 str1 [0…i] 和 str2 [0…j] 的字符串最长子序列长度是多长,但是不一定要以 str [i] 和 str [j] 结尾的,所以跟上面这个点不一样
所以答案就是右下角的值
看所有公共子序列的最后个字符是谁
- 不 i 不 j 结尾,那么有没有这个都一样,那么就跟 dp [i-1][j-1] 一样
- 不 i 以 j 结尾,那么有没有这个 i 都一样,那么就跟 dp [i-1][j] 一样
- 以 i 不 j 结尾,那么有没有这个 j 都一样,那么就跟 dp [i][j-1] 一样
- 以 i 不以结尾,那么有没有这个都一样,那么就跟 dp [i][j]+1 一样
这四个当中取最大值就是我们 dp [i][j] 的值
注意第四种可能性只有在 str1 [i]==str2 [j] 这个情况成立之下才可以使用,如果不成立就不参与比较
# 坐船
双指针:
-
先排序数组 arr
-
我们关注 limit/2, 比如说这个 lmit 是 10, 那么 / 2 的值是 5, 我们关心小于等于 5 的最右位置
- 如果这个位置是 - 1, 那么代表有多少数我们就需要多少个船
- 如果位置是越界 (大于数组长度,那就代表 n/2 条,任意两个都可以乘坐一条船)
-
要是有这个位置,我们就相当有两个组,一个边是小于等于 5 的,一边是大于 5 的
-
接着我们看 l 位置的元素加上 R 位置的元素有没有超过 limit
- 如果大于说明这个 5, 跟他后面哪个数都搞定不了,让 l 往左走,一直走到可以搞定为止
- 走到对的位置后,我们就让 R 往右走,一直走到合适的为止
接着这个 3 代表我们可以搞定这边 R 扩展的元素,也就是两个,那个 3 自己往左数两个,跟这个两个 7 对应,这么做一定是最优分配–> 这里有个贪心,我们不要让 L 继续往左走因为只会变小,这个 3 就是为了解决这两个 7 的最好方式,L 此时左边的数应该是给 R 右边更大的数字,而不是针对于现在 R 经过的这些可能还不是最大的这些数
然后就继续同样让 L 往左 R 往右,看能不能搞定剩下的,注意只能搞定两边都有足够长度,不然不要继续扩升.
然后结束了就对于我们当初走的时候给的标记来决定答案:
公式:
注意: b/2 是向上取整 -->
可以(b+1)/2做到跟向上取证的效果
# 最长回文子序列 (范围上的尝试)
我们想要知道 str [i 到 j] 的范围上最长回文子序列是多少,i 和 j 所以二维表 dp
dp [i][j] 就是 str [i 到 j] 的范围上最长回文子序列是多少
所以 dp [0][字符串长度 - 1] 就是我们想要的答案
注意左下半角的区域没有用,怎么可能左边界比有边界大
范围尝试的数据,对角线x=y的数据是最好填写的
- 在这里,全是 1, 就是自己一个字符,所以长度当然都是 1
- 接着填倒数第二条贴脚线,此时就只有两个字符,如果不相等那么就是 1, 如果相等就是 2
上面两个相当于 base case, 其它的:
- 想可能性
- 形成的最长子序列不以 i 开头,不以 j 结尾–> 代表 dp [i][j]=dp [i+1][j-1](想做是一个范围内)
- 形成的最长子序列以 i 开头,不以 j 结尾–> 代表 dp [i][j]=dp [i][j-1]
- 形成的最长子序列不以 i 开头,以 j 结尾–> 代表 dp [i][j]=dp [i+1][j]
- 形成的最长子序列以 i 开头,以 j 结尾 (这个情况必须是 i 位置字符 ==j 位置字符才会有)–> 代表 dp [i][j]=dp [i+1][j-1]+2 (+2 代表 i 和 j 两个字符也加进来了)
- 所以我们这个顺序填表
因为每个格子依靠他的左边,下边和左下边,所以我们先把已经能算出的那些算出来,然后这些会被之后的需要…
# 添加字符变成回文
范围上尝试的模型
str [i 到 j] 的范围上最少添几个,才可以让这个范围的变成回文串
三种可能性
- 搞定 i+1 到 j 位置的字符,然后再加一个搞定 i 位置的字符,所以 dp [i+1][j]+1
- 搞定 i 到 j-1 位置的字符,然后再加一个搞定 j 位置的字符,所以 dp [i][j-1]+1
- 如果 i 位置的和 j 位置的字符一样, 只有在一样的情况下,就看 dp [i+1][j-1]
然后 dp [i][j] 就是三种或者两种 (如果 i 位置不等于 j) 最小值
有了这个最后的值后,我们可以从那个右上角的答案出发去找源自于哪里,从而对我们的原来字符串做添加变成回文
然后接着… 逆着倒回去看从哪里来的,决定到底该加哪个,然后最后到达对角线结束
这张表记录着所有的解,我们可以走其他路就是另外一个解 (虽然不是对于这个问题是正确答案,但是结果也是个回文)
还原路径,当初怎么决策出来的现在怎么还原出去,一定能够得到一个路径的解
# 切割成回文子串的最小分割数
f (i) 代表 i 开始以及以后所有的,最少需要切割几次
- 一开始是 0 位置
- 我们可以让第一个字符自己就是一个回文,然后调用 f (1)
- 我们可以让前两个字符 (必须是回文才可以), 然后调用 f (2)
- …
- 我们可以让前 x 个字符 (必须是回文才可以), 然后调用 f (x)
所以这里是只有可能这三个,这三个选个最小的就是答案
# 无序数组中找最小第 k 个数
可以荷兰问题递归
- 就是 partition, 随机选个数,左边都是小于的数,然后中间等于这个数,右边都是大于这个数
- 然后靠下标看我们的此时有没有包括住第 k 小的数,如果没有就递归左边 / 右边
- parition 本身就是 O (N) 复杂度,现在就是看递归是要多久
- 用 master 公式,因为是随机选一个数作为 partiiton, 这个算法考虑递归是 O (N)
如果不是随机选数,最差情况可能是 O (N2), 笔试这么解没问题
但是可以有更好,不需要选随机数就可以达到 O (N) 复杂度的算法
# BFPRT
- 不是随机选个数,而是有讲究的选一个数 (跟上面方式的唯一区别)
- 用这个数做 partition
- 如果中间区域没有就看下标情况去递归左边或者右边
怎么有讲究的选一个数?
-
一开始无序数组按照下标分组,每五个分一组,剩下如果不够五个的也分一组
-
每一组选一个中位数,放进一个 Marray 数组里面 (O (N) 的时间复杂度)
-
求 Marray 数组的中位数 (不是 medium, 而是中间那个元素,如果比如说是 4 个元素那就是第二个元素)
怎么求?
就是调用我们整个算法的本身,只不过用一个数,这个数是 Marray 数组长度 / 2 在 Marray 数组 parition 然后递归去找,找出来的肯定是中位数,这个中位数就是我们要很讲究选的数
这样就不需要用概率随机选一个数,平均下来才达到整个算法 O (N), 而是可以直接有讲究的选一个数达到严格的 O (N)
所有组的中位数的中位数,能确保原数组里面肯定有一些数是大于这个数的,所以不可能会出现最差情况
整体严格 O (N) 时间复杂度
# 裂开的方法数
改 dp:
斜率优化:
试试看周围的格子是依赖哪些得出来的,然后找规律,这么做可以省掉枚举行为 (就是那第三个 for loop, 也就是一个格子需要多个格子 (所以 for loop) 去找那些格子做些计算算出当前的)
上方的就是 (优化后):
# 符合搜索二叉树的最大拓扑结构
https://www.bilibili.com/video/BV1W3411W7yi?p=47 [1:00:10 左右]
# 改变数组排序 (完美洗牌问题)
我们想要 O (1) 空间复杂度解决这个问题那就必须需要完美洗牌问题 (时间复杂度 O (NlogN))
我们可以用下表算出一个元素应该在哪个位置
我们可以使用下标循环推,就是一开始元素获取到正确位置怼过去,原本在那个位置的存住然后继续哪个位置的算推到他对应的位置,… 直到推完
但是有个问题,可能形成环,但是中间有元素没处理
比如说:
不一定是一个大环,而是有可能是多个小环,而且每个小环一定不相交
我们应该想选哪些点可以把所有的下标都推到正确的位置上去
所以,有点奇怪,出发点计算:
- 只有 n 是 2,8,26, 或者…(符合 3k-1) 的时候
- 触发点就是 1,3,9,…, 一直到 3k-1
这样我们就有了所有下标出发点,我们所有这些位置都玩一下下标循环推,最终答案啊就是正确的
- 如果这个数组长度 n 是偶数不符合 3k-1 的时候
需要了解一个算法原型,就是如果一个数组想要一部分区域移到另外一个区域,比如
我们可以左右指针,给左区域逆序,给右区域逆序,然后整个再逆序,最终结果就是想要的:
额外空间复杂度 O (1)
然后接着说我们的问题,我们可以找当前这个长度跟哪个符合 3k-1 的数字,比如说我们 N=14
最近 14 且符合 3k-1 的数字是 8
那么我们可以先处理这一部分
怎么做到?其实就是我们所说的上面的那个算法模型:
然后上面那个长度为 8 的按照我们之前说的方式搞定之后我们就可以搞剩下的这部分
我们接着找此时长度 6 最近且符合 3k-1 的数字,也就是 2, 然后我们接着做…, 直到所有处理完就完事
因为我们 N 处理的是偶数张牌,所以肯定就是偶数,肯定会最后被拆分成多个 3k-1 的区域处理完
有些变形仔细想想就知道了,比如说可能会有奇数长度,我们可以一开始把一个数留着不参与之后处理完再处理这个一开始的数等等等
# 正则匹配
注意 * 是 * 前面的那个字符 (pattern) 可以在 str 那个位置出现 0 个,1 个,多个,…
从左到右的尝试模型 f (str,exp,si,ei)
- str 原字符串
- exp 原 pattern 字符串
- str [si… 到往后所有] 能不能被 exp [ei… 到往后所有] 配出来
所以是两个字符串都是从左往右尝试的模型,所以可以就是一个二维表
普通尝试:
可以分为两个大情况
- 如果 ei+1 位置不是 *, 那么 ei 位置一定要跟 si 位置一样,或者 ei 位置是个.
- 如果 ei+1 位置是 *, 那当前这个位置就要试 0 个,1 个,等等等 (取决于能跟 str 匹配多少长度前缀) 看看哪个符合
注意这个如果 ei+1 位置是 *, 我们就需要 while loop 测,只要当前字符能匹配或者有可能性匹配 (考虑到之后的字符,因为有那个 *), 那么我们就继续,直到我们测到确实可以匹配返回 false, 不然一直测测到头 si==s.length 了,那就是不匹配,返回 false, 接着处理下一段,直接把当前字符以及后面的紧跟的 * 看做是 0 个字符
那个 while 循环里面就是不停试如果这个 e 的字符和 e+1 的 * 看做是 0 个那个字符,那么剩下的 (从 e+2) 位置开始,可不可以产出匹配成功的结果,如果不行,那就把这个 e 的字符和 e+1 的 * 看做是 1 个那个字符 (就是抵消掉了一个 s 里面的那个字符), 看看剩下的 (从 e+2) 位置开始能不能匹配…
si++ 就代表目前看来已经再次解决掉了一个那个字符,注意只有在 while 循环那个条件成立才可以,这个也有他妙处,想想 s 是 wasd 然后 e 是.*, 循环会一直进行直到 si==s.length, 然后最后 return 那里然后 base case, 然后 true 了,也就是我们 s 字符串每一个字符都被我们 while 一个一个抵消掉了
动态规划
这里遇到了一个问题,就是初始数据不足,无法推出其他的数
我们可以回到原题意,把该填的地方都填了,剩下的才按照递归改动态规划
这里,一个任一个字按照我们递归可能依赖左下角格子,和此 col+2 的 col 的所有次 row 到结尾 row 的数据, 所以我们需要至少右边有两列,然后最后一行也都有数据,之后其他的就可以依赖彼此一个一个被填
注意 dp 表中任何一个地方,按照我们的递归想法,如过那个位置的 e 的字符是 *, 所以不需要考虑那个位置的 e 的字符是 * 的可能性,因为我们递归的想法是我们不考虑当前 ei 位置是 * 字符,注意那个 isValid 函数和 ei+2, 我们不关心
就算 dp 表需要会到那些东西,我们递归如果不考虑的话,那就不用担心,因为不会被依赖 (用到)
这段填初始值的操作 https://www.bilibili.com/video/BV13g41157hK?p=37 [53:00 左右], 很细节
# 子数组的最大异或和
- 暴力 (O (N3))-> 三个 nested for 循环
- 稍微好一点 (数学加预处理)(O (N2)):
- 前缀树加贪心 (最优)
https://www.bilibili.com/video/BV13g41157hK?p=37 [1:30:00 左右]
# 打爆气球
- 这里就是不停尝试,看看哪个适合,我们尝试哪个气球先打爆,但是这样会很麻烦 (使用范围上尝试的模型), 因为需要很多参数,非常耗空间
- 我们改为了哪个气球最后被打爆这种尝试 ->f (L,R), 潜台词就是 L-1 位置的气球一定没有爆,R+1 位置的气球一定没爆 (这个就是潜台词,大问题定的,小问题遵守,这样可变参数可变少)
比如说参数就是
比如说我们选择 f (1,6)
我们尝试每个位置的气球最后打爆:
-
1 位置的气球最后爆,调用 f (2,6)(这个完全可以,以为满足了潜台词,潜台词就是 L-1 位置的气球一定没有爆,R+1 位置的气球一定没爆)
所以结果就是分数就是 f (2,6)+1*3*1, 因为我们选择当前 1 位置的气球最后打爆
-
6 位置的气球最后爆,调用 f (1,5)(这个完全可以,以为满足了潜台词,潜台词就是 L-1 位置的气球一定没有爆,R+1 位置的气球一定没爆)
所以结果就是分数就是 f (1,5)+1*2*1, 因为我们选择当前 6 位置的气球最后打爆
-
2 位置的气球最后爆,调用 f (1,1) 和 f (3,6)(这个完全可以,以为满足了潜台词,潜台词就是 L-1 位置的气球一定没有爆,R+1 位置的气球一定没爆,这两个调用都符合)
所以结果就是分数就是 f (1,1)+f (3,6)+1*2*1, 因为我们选择当前 2 位置的气球最后打爆
…(其他的都可以)
气球最后爆的尝试方式就需要两个可变参数
改 dp:
使用记忆法,这个经过测试发现无法斜率优化提升,所以记忆优化就行了
# 汉诺塔变形问题
- https://www.bilibili.com/video/BV13g41157hK?p=37 [2:10:00 左右]
迭代方式:
# 分解字符串
https://www.bilibili.com/video/BV13g41157hK?p=38 一开始
# 包含字符串的最短子串
滑动窗口
- 欠债表,一开始记录缺哪些,有可能负数代表我们窗口有更多那个字符
- all 变量,存着总共还欠几个
- 长度,每次达标更新这个变量
如果欠债表出现有一些是 0, 有一些是负数,需要左边往右走,直到都是 0, 算是得到了一个符合的窗口,更新答案,右边继续扩
# LFU
二维双向链表结构才能解决
- 我们有个桶,每个桶存那个词频出现的数据,比如说 A 出现一次我们把 A 和他的 value 包装成一个节点放进桶里面,之后要有其他节点也是词频 1 次,我们也存进去,只不过此时是双向链表结构
这个桶记录着当前存着的双向链表的头和尾
- 我们还有个 map,key 比如说可以是 “A”,value 是那个 A 和他的 value 包装成的节点,我们可以获取到那个节点,然后获取到真正的 value (* 这种用 map 让你 value 指向其他的结构中的存在的地址等这种操作很重要的!!!*)
比如上面我们可以用这个 map 找 B 的节点,hence 他的 value. 而不是需要去遍历那个双向链表
这么做之后要是有比如说词频为 2 的,我们需要给那个建个桶,然后让这个桶跟我们的第一个桶本身之前双向链表连接
每个桶是双向链表结构,每个桶里面的节点也是双向链表结构.
这么做的好处就是每次操作就是 O (1) 的,我们可以通过 map 快速获取到一个节点,然后检查当前有没有比他本身原来词频数大 1 的桶来装此时操作完的这个节点,如果没有就新建,如果有就加进去那里面的双向链表,还有如果当前存在的桶没有节点了,那就销毁。这些操作都是 O (1) 的
如果想要总共存满了,想要 add 新的数据,那么需要替换掉词频最小的,要是词频都一样的话那就替换时间最早的. 这不就是让当前头桶的_头_节点去除掉,然后把当前加的节点放进正确地方去吗
# 加油站
- 首先把油数组减去距离数组,获取每一个点出发,自己的油减去距离下一站的距离到了那个站之后剩下的多少油,这个数组叫做纯能数组
- 这么做我们就可以把问题变成沿途累加和是否小于 0
比如说我们获取到了
此时我们可以比如说
- 0 号位置出发,一开始就是 - 1, 所以不可能
- 1 号位置出发,一开始就是 1, 到下一站 - 2, 去和的结果变成 - 1, 所以不可能
- 2 号位置出发,一开始就是 - 2, 所以不可能
- 3 号位置出发,一开始 2, 下一站 3, 下一站 2, 下一站 3, 下一站 1 回到了出发点,所以可以,这个为 true
- 4 号位置出发,一开始 1, 下一站 0, 下一站 1, 下一站 - 1, 所以不可能
但是我们这么做每个节点都尝试出发,那就是 O (N2) 方法,如何做到 O (N)?
一开始选一个可能成功的点出发 (所以必不能是负数,如果都是负数那就都不可能直接返回), 例子选择 H 作为出发点
- 联通区代表,左闭右开,一开始是 [H,I), 左闭右开是因为一开始此时 H 只能到得了 H (还没走 yet)
- rest 表示通过了联通区后,我们还剩多少油
- need 代表如果当前的节点要接到联通区的头上,需要至少多少油,现在一开始我们就在 H 所以我们并不需要就等于 0
接着我们尝试往逆时针方向扩,此时和为 5-4=1, 可以扩,所以我们此时
此时再扩发现不行了,1-2=-1, 是负数,所以 H 不是良好的出发点,我们需要来到 H 的逆时针方向,也就是 G 点,我们尝试让他变成联通区存的头,因为 G 点是 2, 所以 need 还是 0 (只要那个变成头的节点存的不是负数那么 need 就是 0),rest 值也变了,此时就变成了
注意原本区域结尾什么的都还没变,我们还没扩到 A, 左闭右开!
接着我们尝试尾巴让下扩,发现 ok,rest 还是正数
就各种扩等等等… 直到
此时尝试扩 C 发现不行就知道 G 不是良好出发点,我们需要再次让头部变成左边的,也就是 F 点.
但是 F 不满足接到联通区头部的要求,因为他是负数,直接标记 F 为不良好出发点,然后 need 变成 2!!!
这个代表以后的节点想接到联通区的头部要求增加了,以为他要连 F, 然后 F 是 - 2, 你新头部需要承担 F 的这个负的代价,继续往左边扩,发现 E 也是 - 1, 不符合,标记不良好,然后 need 变成 - 3, 继续… 来到 D,D 满足要求,此时 need3-3=0,rest 保持不变因为 D 已经把他那个 3 给支付掉了作为 F 和 E 的代价,所以无法给到尾部用来扩。此时头部更新好了,尾部继续扩…
这个例子中哦我们最后头来到了 D 然后尾尝试扩到 C 但是失败,我们扩头也会碰到 C, 这个情况的话,就不需要再继续验了,C 和 B 和 A 和 I 肯定都是不良好的出发节点
证明:
https://www.bilibili.com/video/BV1W3411W7yi?p=50 [18:00 左右]
上面例子是都是不良好出发点,另外一个例子:
这个例子我们发现 H 是良好出发点,可以转一圈
我们接着就用他结束之后剩下的哪个 need 的值 (因为 H 是转了一圈的,良好出发点,所以 need 应该是 0), 我们接着就忘他左边去看,能不能接上那个 H 的头,只要他能接上头,那么那个也是个良好的出发点,最后联通区就是 [H,H)
不用关心尾了,只要能接上头就是良好出发点,能接上头到哪里都行
- G 是 - 1, 不行,need 变成 1
- F 导致 need 变成 0, 可以
- E 导致 need 变成 - 1, 不可以
- D 导致 need 变成 - 2, 不可以
- C 导致 need 变成 0, 可以
- B 导致 need 变成 - 4, 不可以
- A 导致 need 变成 - 1, 不可以
当然要是这期间遇上之前我们一开始再找良好出发点的时候已经被标记为不良好出发点那就不用管了,直接设置完事
所以这个只是转了这个圈一圈,必然是 O (N)
有点像窗口
# 抽烟矩阵
# 首先需要了解线段问题
- 把开始位置排序
- 接着把数据放入有序表, 有序表按照结尾排序!!!
- 首先是 1 到 9, 需要把有序表所有小于或者等于 1 的数字丢出去 (没有扔,因为没有数), 然后放入 9, 此时有序表有一个数,就是处理 1 到 9 这个线段的答案,也就是 1
- 然后是 2 到 5, 需要把有序表所有小于或者等于 2 的数字丢出去 (没有扔,因为就一个 9), 然后放入 5, 此时有序表有两个数,就是处理 2 到 5 这个线段的答案,也就是 2
- 然后是 2 到 4, 需要把有序表所有小于或者等于 2 的数字丢出去 (没有扔,因为 9,5 都比 2 大), 然后放入 4, 此时有序表有三个数,就是处理 2 到 4 这个线段的答案,也就是 3
- 然后是 3 到 10, 需要把有序表所有小于或者等于 3 的数字丢出去 (没有扔,因为 9,5,4 都比 3 大), 然后放入 10, 此时有序表有四个数,就是处理 3 到 10 这个线段的答案,也就是 4 (最终答案)
- 然后是 6 到 8, 需要把有序表所有小于或者等于 6 的数字丢出去 (扔掉了 4 和 5), 然后放入 8, 此时有序表有三个数,就是处理 6 到 8 这个线段的答案,也就是 3
每个线段都有一个答案,最大的答案就是我们需要的答案
每个线段的答案的含义是我们重合区域必须以那个线段开头 (比如说 1 到 10 就是必须以 1 开头) 开头的情况下,我们目前处理完了的这些线段来说,最多盖几块
如果有 N 个线段,处理每一个线段代价 O (logN)<- 有序表的增删改查
所以解法总共是 O (NlogN)
# 矩阵问题继续解答
任何重叠的区域一定是某一个矩形的底
- 所以我们可以首先把所有矩形按照矩形底边排序
- 先处理在最下面的矩形,往上一个一个处理
- 我们记录所有在当前矩形底部的一整个横线上
- 然后对于其他所有加的矩阵我们首先需要看谁的上边还没比到我们当前要加的低边高的矩阵,我们要把他们把那些从容器中都移出
这样对于每一个矩阵我们知道一共有多少个矩阵上面比当前矩阵底部高且比底部当前矩阵底部底
然后我们可以取出那些矩阵的 x 宽度,这些宽度相当于就是一个个线段,这样矩阵的问题被我们变成了一维线段问题,调用上面我们说的那个算法原型 (线段问题), 最后答案就出来了
# 技巧
-
再有序数组中找最 (左 / 右) 位置的大于等于的可以用二分查找
-
打表法:如果输入输出都是 int, 可以直接弄一个很傻的结局方法然后接着拿很多个输入参数来测,打印每一个的输出,接着看输出看有什么规律,直接按照规律写代码 (并不是所有的整数型题目都这样)
-
预处理:研究代码,看哪一块是频繁的,比如说对于数组中每一个元素都要往前 O (N) 遍历找到什么什么信息什么的。完全可先遍历等等等用多余的数据结构 (可以是多个) 存下相关的信息,之后需要信息, 就不需要重复的进行那个可能会很耗时的操作,而是直接靠下标获取对应的想要的值就行了
注意这个装信息的数据结构,在填信息的时候尽量要如何快速地填信息,参考_矩阵最大正方形边长边框_问题的优化做法,多考虑,别什么都想遍历
-
注意开始,结束位置,该怎么走,往那边走 (遍历) 啥的
-
多想想如果怎么怎么样,等等等列出各种可能性
-
如果数量太多,先想对于一个来说怎么怎么样,列出各种可能性等等等
-
多考虑,遍历的时候可以算出当前位置左边有多少个位置,右边有多少位置的,不过要是想要知道当前位置左边所有的元素的加 (比方说) 或者当前位置右边所有的元素的加,我们就需要边遍历边拿一个变量存着!注意遍历方向等等。别想太复杂,能用变量存着就别想什么数组,只有那个信息是一个或几个变量很难存下的时候我们才用数组什么的
-
矩阵–> 有时候想办法把外面一圈给搞定,再搞定里面的一圈,接着搞定那个的里面的一圈,so on… 直到错位或者…
矩阵有时候不要局部想这一个怎么走怎么走,然后这个走几步那里走几步等等等,这很麻烦!!!
要想得整体一点点,可以把它分成一圈包着一圈,或者一条斜线跟着一条斜线,等等等 (具体看需求), 在这基础上我们还可以接着做分组然后各种操作啊等等等,反正当我们对于当前这一圈 / 一条斜线 (具体看需求) 做完操作了,我们接着处理下一圈 / 下一跳斜线,如果还有的合法的话
-
Arrays.binarySearch (…) 和 Collections.binarySearch (…)
如果查找的 value 包含在数组中,则返回搜索 value 的索引;否则返回 (-(插入点) - 1)。插入点 被定义为将键插入数组的那一点:即第一个大于此键的元素索引,如果数组中的所有元素都小于指定的键,则为 a.length。注意,这保证了当且仅当此键被找到时,返回的值将 >= 0。
即是,有可能返回的是 (负) 插入点的
反正就是你确定当前数在有序数组中都比他大的,那么你就可以用这个找到那个第一个比他大的,这个返回的是个负数比如说 x, 然后
-x-1才是那个第一个比你那个数大的那个数的下标。注意如果数组有你要找的数,那么肯定返回的就是你这个数在数组中的下标.
- tail recursion–> 就是你边回调自己边把这一层的结果传下去,最后到了最后一层我们这个最终结果他也有直接返回,然后会一层层返回回去,注意我们之前上面的那些层我们并没有存任何变量等等等我们只是
return 自己(...,本层的结果);而不是像什么return 自己本层某种变量 +/-/*/...等等等操作 自己(...,本层的结果);所以这么做很省空间,O (1) 的空间! - 大根堆小根堆,各有各的妙处,有时候可能用其中一个很明显,但说不定来外一个也可以 (依靠你检查大小不超过什么什么数等), 这么做我们还可以知道当前进堆最大门槛 / 最小门槛等等等,说不定还可以省空间,只用你规定的空间
- 所以有时候问你问题是需要只用队列 / 栈做什么什么事情,而正常做法应该是用栈 / 队列,我们可以考虑用两个栈实现队列或者两个队列实现栈,然后做相对应操作
- 多个区域,想一想哪个位置是必须包括的,包括了那些位置之后还需要包括其他的吗还是没有必要或者不符合我们的要求等
- 动态规划,如果不确定要定多大的空间,想需要空间最多的情况需要多少,要实在想不出来,直接就用很大很大一个空间可能也行,但是不好,因为浪费空间
- 树型 dp 时间复杂度就是 O (N), 这是如果我们那个套路每一层的常数操作
- 子数组最大的和的值
如果有多个子数组都有一样的和,那么这个就是针对于最长的那个子数组而取到的 max (其实都一样)
这个就是假设答案法,就是你过一下然后想一下要用什么方式存下,然后去实现
-> 假设答案 -> 分析答案性质 -> 设置流程就能找到答案了
- 子矩阵问题先想子数组怎么办的,子数组问题解决了,就想办法尝试把子矩阵问题压缩成子数组问题
- 构建单调性,可以省略掉复杂度,比如说省掉枚举行为
- 递归有时候不停,我们可以先找平凡解,然后 basecase 用那个平凡解作为限制来确保递归可以最终退出
- 看到子数组或者子串的问题,先想每个位置结尾的情况下怎么怎么样
- dp 范围上尝试,
范围尝试的数据,对角线x=y的数据是最好填写的,然后一般范围上尝试的模型注意开头和结尾!!! 一般都靠开头和结尾怎么样去决定的,想可能性!
范围上尝试就是在看 dp [i][j] 的所有 (i (开不) 开头 j (结不) 结尾) 的可能性分类下,能不能把整个域的问题给解决,这是最关键的,如果不行那就还尝试从左到右模型
所以继续从左往右模型再加一个,从左往右模型就是从左到右 i 位置的要或者不要
如果不清楚就挨个试试,可能性分类就是唯一一个 dp 里面需要动脑子的点
- 有时候改 dp, 你递归 base case 不明显或者…, 总之你 dp 表发现一个格子依赖这些格子,但是我们没有足够初始数据格子让其他格子挨个挨个依赖填好,所以我们需要回到题意,手动给那些最基本,最需要的那些格子给上值,这样我们就可以接着回到递归按照递归改 dp
- 这点适用于 followup 上面那点 (我们需要手动给 dp 初始值): 就算 dp 表需要会到那些东西,我们递归如果不考虑的话,那就不用担心那种可能性,因为不会被依赖 (用到),dp 表每个格子只是承载了,如果递归调用那个位置 (比如说二维 dp, 可变参数 i 和 j, 给到了我们原本递归函数), 我们可以得到什么结果,就是用这两个可变参数此时那个位置的值去调用递归函数的返回值 (或者…)!!!
- 递归定义很多潜台词,是为了之后分为小问题后,可以不用那么多的参数,小问题也需要严格遵守那些规则,否则递归可变参数太多了,很麻烦
- 很多二维的图形问题都需要转换成一维线段问题解决的