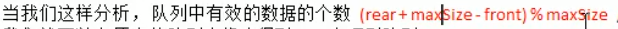My Algorithm and Data Structure Notes
# 
# 稀疏数组和队列
# 1、稀疏数组 [SPARSE ARRAY]
个人总结:
如果一个数组里面存有大量同样的东西,比如说同一个数字,可以考虑用稀疏数组来存这个数组
稀疏数组只记录那些不一样的数字 (value) 应该存在在本来的位置 (which row, which column, etc…)
所以只是记录那些不一样的数字的值以及位置信息,这样不需要存那些大量的重复的值
稀疏数组的第一个 element 应该存着本来数组的 row number and column number 以及有多少他要保存不一样的数字的数量,这样就足以靠着这个稀疏数组得到跟原本数组描述的一样的效果
二维数组 => 稀疏数组
首先遍历二维数组找出不一样的数并且总共有几个不一样的数存到 sum
创建稀疏数组
int[] sparseArr = new int[sum+1][3]
- sum+1 是因为这个稀疏数组第一个 element 保存的是原本数组的 row number, rolumn number, 以及 sum 然后接下来的 elements 才是每个不一样的数字的值和位置
- column 为 3 是因为每个 element (每一行) 要存储 row 的信息,column 的信息以及值的信息
然后把那些不一样的数据传入稀疏数组就行了
这样我们磁盘保存这个就行了,没二维数组那么耗空间
稀疏数组 => 二维数组
- 读取稀疏数组第一行,创建对应的大小的二维数组
- 接着读取稀疏数组后几行的数据把每个赋值在对应的下标位置给的二维数组
这样我们运行的时候就把稀疏数组给加载到内存然后转换成二位数组,然后用来操作其他的各种
# 1.1、实际需求
- 编写的五子棋程序中,有存盘退出和续上盘的功能
- 因为该二维数组的很多值是默认值 0 ,因此记录了很多没有意义的数据,我们将其转为稀疏数组进行存储
# 1.2、稀疏数组应用
# 1.2.1、稀疏数组处理方法
- 稀疏数组把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模
- 稀疏数组也是二维数组,行数由原数组的数据决定,列数一般为 3 列
- 稀疏数组的第一行记录原数组一共有几行几列,有多少个不为零的值
- 第一列:原数组的行数
- 第二列:原数组的列数
- 第三列:原数组有多少个不为零的值
- 之后的行记录原数组中不为零(x)的值所在的行数、列数以及 x 的值
- 第一列:x 在原数组中的行数
- 第二列:x 在原数组中的列数
- 第三列:x 的值
# 1.2.2、举例说明
- 原始二维数组较大,压缩后占用空间减少
# 1.3、应用实例
# 1.3.1、思路分析
- 使用稀疏数组, 来保留类似前面的二维数组 (棋盘、 地图等等)
- 把稀疏数组存盘, 并且可以从新恢复原来的二维数组数
# 1.3.2、代码实现
- 代码
public class SparseArray {
public static void main(String[] args) {
// 创建一个原始的二维数组 11 * 11
// 0: 表示没有棋子, 1 表示 黑子 2 表蓝子
int chessArr1[][] = new int[11][11];
chessArr1[1][2] = 1;
chessArr1[2][3] = 2;
chessArr1[4][5] = 2;
// 输出原始的二维数组
System.out.println("原始的二维数组~~");
for (int[] row : chessArr1) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
// 将二维数组 转 稀疏数组的思
// 1. 先遍历二维数组 得到非0数据的个数
int sum = 0;
for (int i = 0; i < chessArr1.length; i++) {
for (int j = 0; j < chessArr1[i].length; j++) {
if (chessArr1[i][j] != 0) {
sum++;
}
}
}
// 2. 创建对应的稀疏数组
int sparseArr[][] = new int[sum + 1][3];
// 给稀疏数组赋值
sparseArr[0][0] = chessArr1.length;
sparseArr[0][1] = chessArr1[0].length;
sparseArr[0][2] = sum;
// 遍历二维数组,将非0的值存放到 sparseArr中
int count = 0; // count 用于记录是第几个非0数据
for (int i = 0; i < chessArr1.length; i++) {
for (int j = 0; j < chessArr1[i].length; j++) {
if (chessArr1[i][j] != 0) {
count++;
sparseArr[count][0] = i;
sparseArr[count][1] = j;
sparseArr[count][2] = chessArr1[i][j];
}
}
}
// 输出稀疏数组的形式
System.out.println();
System.out.println("得到稀疏数组为~~~~");
for (int i = 0; i < sparseArr.length; i++) {
System.out.printf("%d\t%d\t%d\n", sparseArr[i][0], sparseArr[i][1], sparseArr[i][2]);
}
System.out.println();
// 将稀疏数组 --》 恢复成 原始的二维数组
/*
* 1. 先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的 chessArr2 = int [11][11] 2.
* 在读取稀疏数组后几行的数据,并赋给 原始的二维数组 即可.
*/
// 1. 先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组
int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];
// 2. 在读取稀疏数组后几行的数据(从第二行开始),并赋给 原始的二维数组 即可
for (int i = 1; i < sparseArr.length; i++) {
chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}
// 输出恢复后的二维数组
System.out.println();
System.out.println("恢复后的二维数组");
for (int[] row : chessArr2) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
}
}- 程序运行结果
原始的二维数组~~
0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0
0 0 0 2 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 2 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
得到稀疏数组为~~~~
11 11 3
1 2 1
2 3 2
4 5 2
恢复后的二维数组
0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0
0 0 0 2 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 2 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0# 1.4、课后练习
- 在前面的基础上, 将稀疏数组保存到磁盘上, 比如 map.data
- 恢复原来的数组时, 读取 map.data 进行恢复
# 2、队列 [QUEUE]
个人理解:
- 先进先出 FIFO
- 两种实现方式
- 数组
- 链表
如果使用数组方式实现:
- 队列像是个类,然后有
一个成员数组存储着数据 (数组本来就是有序,连续的,所以这个队列也是)
一个成员 maxSize 代表这个队列的最大容量
有一个成员为 front 记录当前__存在于__队列排在最前面的那个元素的下标 - 1
有一个成员为 rear 记录当前__存在于__队列排在最后面的那个元素的下标
一开始,rear 和 front 都是 - 1
rear-front 等于当前列表存的数据的数量
- 有一个 isFull 方法, 如果 rear=maxSize-1, 代表这个 rear 现在指向的元素就是当前队列存的最后一个元素,所以返回 true
- 有一个 isEmpty 方法, 如果 rear==front 代表当前列表为空,返回 true
- 有一个 addDataToQueue 方法,如果 isFull 返回 false 则
- rear++ 然后
- 把加的数据加到当前 data 数组的下标为 rear 的位置
- 有一个 getDataFromQueue 方法,如果 isEmpty 返回 false 则
- front++ 然后
- 把 data 数组的下标为 front 的数据给返回出去 (代表不在队列中了)
但是注意我们上面的实现方式有问题,因为取出来的那些元素那些空间我们之后不能再用了,应该是还能用的,所以我们考虑
__用数组模拟一个环形队列 [CIRCULAR QUEUE] __
队列:只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
1. 循环队列
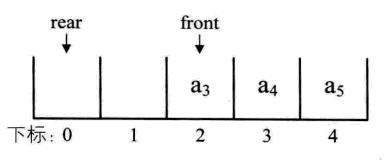
队列的顺序储存结构:用数组存储队列,引入 front 指针指向队头元素,rear 指针指向队尾元素的下一个位置,当 front=rear 时,为空队列,结构如下图所示。
当执行入队操作时,若数组尾部已满,而数组前部因有元素出队而有空位时,我们把新插入的元素从头开始入队,这样就类似于头尾相接的结构。
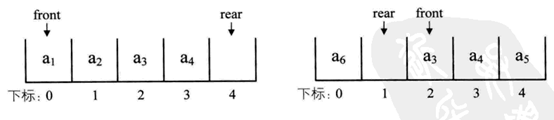
队列的这种头尾相接的顺序存储结构称为循环队列,如下图所示。
上面队列的定义中提到,当 front=rear 时,为空队列,而在循环队列中,队列满时,front 也等于 rear,将无法判断队满和空的情况。
一种办法是设置一个标志变量 flag,当 front=rear 时,通过判断 flag 是 0 还是 1 来确定队列满空情况;
另一种方法是,在数组中只剩一个空闲单位时,定义为队列满,如下图所示。(本文程序采用这种办法)
因为 rear 可能比 front 大,也可能比 front 小,所以队列满的条件应该为:(rear+1)%maxSize==front;同理,队列长度的计算公式为:(rear-front+maxSize)%maxSize。
这里也就是:
一开始 front 和 rear 都等于 0
front 指向数组中第一个数据的下标
rear 指向数组中最后一个数据的下标 + 1, 这个 1 其实就是代表我们希望空出来一个空间作为约定
如果 (rear+1)% maxSize=front 就代表当前队列满了
如果 rear==front 就代表当前队列时空的
加入一个数据时
- 判断是不是已经满了
- 不满的话加入到 rear 现在的位置 (下标)
- rear++ % maxSize (% maxSize 是为了确保不超出队列的最大大小,所以 rear 的值最大也不会超过 maxSize-1)
取出一个数据时
- 判断是不是已经空了
- 不是空的话取出 front 现在的位置 (下标) 的元素
- front++ % maxSize (% maxSize 是为了确保不超出队列的最大大小,所以 front 的值最大也不会超过 maxSize-1)
可以看出如果一直取出取出,直到取出最后一个元素时 front==rear (此时 rear 指向的就是那个空出来的空间) 说明为空
要是我们要是不特意留空出来一个空间,而是用来存数据的,也就是我们 maxSize 设的是什么,这个队列就能存多少数据,那么当我们存满了,此时 rear 指向最后一个元素 + 1, 这个时候 rear 会是 ==front 的,所以 rear 的位置需要是个空元素,就算满了的时候,rear 的位置也是空出来的,所以就算满了 rear 的位置也不会是等于 front, 这也就说明这种实现方式这个队列最多只能存 maxSize-1 个数据
比方说:
- 新建一个 maxSize 为 3 的队列
- front = 0 and rear = 0
- 添加两个元素进去
- front = 0 and rear = 2
- 此时 rear (下标为 2) 的就是那个空的,而且 (rear+1)% maxSize=front->(2+1)%3=0, 是真的,所以现在队列为满
- 取出一个元素
- front 的位置取出,然后__front=(front+1)% maxSize__, 所以现在 front 等于 1
- 再添加一个元素
- 每次添加都会让__rear=(rear+1)% maxSize__的下标位置,也就是 (2+1)%3=0, 下标为 0 的位置
- 所以 rear 现在等于 0 (下标位置), 而那个添加的是会添加到下标为 2 的位置
- 此时 rear (下标为 0) 的就是那个空的,而且 (rear+1)% maxSize=front->(0+1)%3=1, 是真的,所以现在队列为满
- 取出两个元素 (应该为空了)
- front 在第二个元素取出后,front=(front (此时为 2)+1)% maxSize (3)=0
- 所以 rear==front, 确实为空
所以那个空位置主要是为了让 rear 永远会在满的时候不等于 front
只有队列为空的时候才会是 rear==front
队列最多能装有 maxSize-1 个数据
rear 可能会比 front 小,rear 也可能会比 front 大
每次添加 / 取出 -> 让 rear 或者 front+1 更新位置,需要 % maxSize 一下让他不会超过下标为 maxSize-1 的值 (imagine a circle)
在队列满的时候
- (rear+1) 如果不是等于 maxSize 的话就一定会是 front 的下标 -> 也就是 rear 的值比 front 小
- 但是当然 rear 的值也可能比 front 大 (只有在 rear 的下标位置为 maxSize-1 时候才会队列又满而且 rear 比 front 大), 那么 rear+1 就会等于 maxSize, 这个就已经超出了当前队列的下标最大大小,所以需要 % maxSize 一下获取到他在队列里面真正属于的下标位置,也就是 rear+1=maxSize, 而 maxSize% maxSize 当然等于 0, 而因为队列是满的所以 front 也肯定是 0 (以为此时 rear=maxSize-1), 所以
不管哪种情况 ->(rear+1)% maxSize=front 的话证明当前队列为满
在队列为空的时候
- 我们知道每次取出一个数据之后,front 就会往__(按顺序) 下一个__循环队列的中的下标位置跳
- 所以在清除最后一个数据后,front 会往__(按顺序) 下一个__循环队列的中的下标位置跳,因为 ((front+1)% maxSize) 所以不管怎么样最后 front 会跳到 rear 的位置,也就是那个空的空间,也就是那个有数据的时候在最后一个数据的下一个坐标,所以在 front==rear 的时候,队列为空
这个是因为 rear-front 能获得有多少数据,但是这是只有 rear 比 front 大的情况下是真的
要是 rear 比 front 小,我们可以先给 rear 加上 maxSize, 这样这个总数一定比 front 大,获得他们的差值然后取模 maxSize 相当于把之前加的 maxSize 给取消了 (这个只有在 rear 比 front 大的情况下才会起作用,因为要是 rear 比 front 小,那么 rear-front 是负数再加上 maxSize 会让 maxSize 更小), 就可以获得有多少数据
- rear 是 4 front 是 2 maxSize 是 10
- (4+10-2)%10= 12%10 =2 之前加的 10 没有效果
- rear 是 2 front 是 4 maxSize 是 10
- (2+10-4)%10= 8%10 =2 之后 %10 没有效果
记住这个取模技巧!!!
# 2.1、队列使用场景
- 银行排队的案例:
# 2.2、队列介绍
- 队列是一个有序列表, 可以用数组或是链表来实现。
- 遵循先入先出的原则, 即: 先存入队列的数据, 要先取出,后存入的要后取出
- 示意图: (使用数组模拟队列示意图)
# 2.3、数组模拟队列
# 2.3.1、思路分析
- maxSize :队列容量(数组的长度)
- arr :模拟队列的数组
- front :指向队列头部元素的前一个元素,初始值为 -1
- rear :指向队列尾部元素,初始值为 -1
- 基本操作
- 队列判空:front == rear
- 队列判满:rear == (maxSize - 1) ,即 rear 是否已经指向了数组的最后一个位置
- 队列元素个数:rear - front
- 队列入队:队列不满才能入队,arr [++rear] = value
- 队列出队:队列不空才能出队,return arr [front++]
# 2.3.2、代码实现
- 队列的定义
// 使用数组模拟队列-编写一个ArrayQueue类
class ArrayQueue {
private int maxSize; // 表示数组的最大容量
private int front; // 队列头
private int rear; // 队列尾
private int[] arr; // 该数据用于存放数据, 模拟队列
// 创建队列的构造器
public ArrayQueue(int arrMaxSize) {
maxSize = arrMaxSize;
arr = new int[maxSize];
front = -1; // 指向队列头部,分析出front是指向队列头的前一个位置.
rear = -1; // 指向队列尾,指向队列尾的数据(即就是队列最后一个数据)
}
// 判断队列是否满
public boolean isFull() {
return rear == maxSize - 1;
}
// 判断队列是否为空
public boolean isEmpty() {
return rear == front;
}
// 添加数据到队列
public void addQueue(int n) {
// 判断队列是否满
if (isFull()) {
System.out.println("队列满,不能加入数据~");
return;
}
rear++; // 让 rear 后移
arr[rear] = n;
}
// 获取队列的数据, 出队列
public int getQueue() {
// 判断队列是否空
if (isEmpty()) {
// 通过抛出异常
throw new RuntimeException("队列空,不能取数据");
}
front++; // front后移
return arr[front];
}
// 显示队列的所有数据
public void showQueue() {
// 遍历
if (isEmpty()) {
System.out.println("队列空的,没有数据~~");
return;
}
for (int i = front + 1; i <= rear; i++) {
// Java 中也能用占位符诶
System.out.printf("arr[%d]=%d\n", i, arr[i]);
}
}
// 显示队列的头数据, 注意不是取出数据
public int headQueue() {
// 判断
if (isEmpty()) {
throw new RuntimeException("队列空的,没有数据~~");
}
return arr[front + 1];
}
}- 测试代码
public class ArrayQueueDemo {
public static void main(String[] args) {
// 测试一把
// 创建一个队列
ArrayQueue queue = new ArrayQueue(3);
char key = ' '; // 接收用户输入
Scanner scanner = new Scanner(System.in);//
boolean loop = true;
// 输出一个菜单
while (loop) {
System.out.println("s(show): 显示队列");
System.out.println("e(exit): 退出程序");
System.out.println("a(add): 添加数据到队列");
System.out.println("g(get): 从队列取出数据");
System.out.println("h(head): 查看队列头的数据");
System.out.println();
key = scanner.next().charAt(0);// 接收一个字符
switch (key) {
case 's':
queue.showQueue();
break;
case 'a':
System.out.println("输出一个数");
int value = scanner.nextInt();
queue.addQueue(value);
break;
case 'g': // 取出数据
try {
int res = queue.getQueue();
System.out.printf("取出的数据是%d\n", res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case 'h': // 查看队列头的数据
try {
int res = queue.headQueue();
System.out.printf("队列头的数据是%d\n", res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case 'e': // 退出
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("程序退出~~");
}
}- 程序运行结果
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
s
队列空的,没有数据~~
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
a
输出一个数
1
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
a
输出一个数
2
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
a
输出一个数
3
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
s
arr[0]=1
arr[1]=2
arr[2]=3
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
a
输出一个数
4
队列满,不能加入数据~
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
g
取出的数据是1
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
g
取出的数据是2
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
g
取出的数据是3
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
g
队列空,不能取数据
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据# 2.4、数组模型环形队列
# 2.4.1、提出问题
- 目前数组使用一次就不能用, 没有达到复用的效果,造成内存空间的浪费
- 将这个数组使用算法, 改进成一个环形的队列(取模: %)
# 2.4.2、思路分析
- 对前面的队列进行优化,改造为环形队列(通过取模实现)
- maxSize :队列容量(数组的长度)
- arr :模拟队列的数组
- front :指向队列头部元素,初始值为 0
- rear :指向队列尾部元素的后一个元素,初始值为 0
- 基本操作
- 队列判空:front == rear
- 队列判满:
- 为何要在 rear 之后,front 之前空出一个元素的空间?因为如果不空出一个元素,队列判空条件为:front == rear ,队列判满的条件也是:front == rear ,有歧义!
- 队列容量:因为空出了一个元素,所以队列容量就变成了 (maxSize - 1)
- 当空出一个元素的空间,如何判满?当还剩一个元素时,队列就已经满了,所以判断条件为 (rear + 1) % maxSize == front
- 队列元数个数:
- 计算公式:(rear + maxSize - front) % maxSize ,这样来思考:
- 当 rear 比 front 大时,即 (rear - front) > 0 ,这时还没有形成环形结构,(rear - front) 即是队列元素个数
- 当 rear 比 front 小时,即 (rear - front) < 0 ,这时已经形成了环形结构,(rear - front) 表示数组还差多少个元素存满(负数),(rear + maxSize - front) 即是队列元素个数
- 综上:(rear + maxSize - front) % maxSize
- 队列入队:
- 首先,队列不满才能入队
- 由于 rear 指向队列尾部元素的后一个元素,所以直接设置即可: arr [rear] = value
- 接下来,rear 应该向后移动一个位置:rear = (rear + 1) % maxSize
- 取模是为了防止数组越界,让指针从新回到数组第一个元素
- 队列出队:
- 首先,队列不空才能出队
- 由于 front 直接指向队列头部元素,所以直接返回该元素即可:int value = arr [front]
- 接下来,front 应该向后移动一个位置:front = (front + 1) % maxSize
- 取模是为了防止数组越界,让指针从新回到数组第一个元素
# 2.4.3、代码实现
- 环形队列的实现
class CircleArray {
private int maxSize; // 表示数组的最大容量
// front 变量的含义做一个调整: front 就指向队列的第一个元素, 也就是说 arr[front] 就是队列的第一个元素
// front 的初始值 = 0
private int front;
// rear 变量的含义做一个调整:rear 指向队列的最后一个元素的后一个位置. 因为希望空出一个空间做为约定.
// rear 的初始值 = 0
private int rear; // 队列尾
private int[] arr; // 该数据用于存放数据, 模拟队列
public CircleArray(int arrMaxSize) {
maxSize = arrMaxSize;
arr = new int[maxSize];
}
// 判断队列是否满
public boolean isFull() {
return (rear + 1) % maxSize == front;
}
// 判断队列是否为空
public boolean isEmpty() {
return rear == front;
}
// 添加数据到队列
public void addQueue(int n) {
// 判断队列是否满
if (isFull()) {
System.out.println("队列满,不能加入数据~");
return;
}
// 直接将数据加入
arr[rear] = n;
// 将 rear 后移, 这里必须考虑取模
rear = (rear + 1) % maxSize;
}
// 获取队列的数据, 出队列
public int getQueue() {
// 判断队列是否空
if (isEmpty()) {
// 通过抛出异常
throw new RuntimeException("队列空,不能取数据");
}
// 这里需要分析出 front是指向队列的第一个元素
// 1. 先把 front 对应的值保留到一个临时变量
// 2. 将 front 后移, 考虑取模
// 3. 将临时保存的变量返回
int value = arr[front];
front = (front + 1) % maxSize;
return value;
}
// 显示队列的所有数据
public void showQueue() {
// 遍历
if (isEmpty()) {
System.out.println("队列空的,没有数据~~");
return;
}
// 思路:从front开始遍历,遍历多少个元素
// 动脑筋
for (int i = front; i < front + size(); i++) {
System.out.printf("arr[%d]=%d\n", i % maxSize, arr[i % maxSize]);
}
}
// 求出当前队列有效数据的个数
public int size() {
// rear = 2
// front = 1
// maxSize = 3
return (rear + maxSize - front) % maxSize;
}
// 显示队列的头数据, 注意不是取出数据
public int headQueue() {
// 判断
if (isEmpty()) {
throw new RuntimeException("队列空的,没有数据~~");
}
return arr[front];
}
}- 测试代码
public class CircleArrayQueueDemo {
public static void main(String[] args) {
// 测试一把
System.out.println("测试数组模拟环形队列的案例~~~");
// 创建一个环形队列
CircleArray queue = new CircleArray(4); // 说明设置4, 其队列的有效数据最大是3
char key = ' '; // 接收用户输入
Scanner scanner = new Scanner(System.in);//
boolean loop = true;
// 输出一个菜单
while (loop) {
System.out.println("s(show): 显示队列");
System.out.println("e(exit): 退出程序");
System.out.println("a(add): 添加数据到队列");
System.out.println("g(get): 从队列取出数据");
System.out.println("h(head): 查看队列头的数据");
System.out.println();
key = scanner.next().charAt(0);// 接收一个字符
switch (key) {
case 's':
queue.showQueue();
break;
case 'a':
System.out.println("输出一个数");
int value = scanner.nextInt();
queue.addQueue(value);
break;
case 'g': // 取出数据
try {
int res = queue.getQueue();
System.out.printf("取出的数据是%d\n", res);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
break;
case 'h': // 查看队列头的数据
try {
int res = queue.headQueue();
System.out.printf("队列头的数据是%d\n", res);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
break;
case 'e': // 退出
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("程序退出~~");
}
}- 程序运行结果
测试数组模拟环形队列的案例~~~
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
a
输出一个数
1
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
a
输出一个数
2
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
a
输出一个数
3
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
s
arr[0]=1
arr[1]=2
arr[2]=3
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
a
输出一个数
4
队列满,不能加入数据~
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
g
取出的数据是1
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
g
取出的数据是2
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
s
arr[2]=3
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
g
取出的数据是3
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据
g
队列空,不能取数据
s(show): 显示队列
e(exit): 退出程序
a(add): 添加数据到队列
g(get): 从队列取出数据
h(head): 查看队列头的数据# 链表
# 1、链表 (Linked List) 介绍
- 数据的存储地址不是连续的
- 每一个节点有 data 属性存数据有 next 存的是下一个节点对象的地址 (或者 null 代表没有下一个节点对象)
首先有一个 Node 类
- 这个类面有各种属性存放着信息
- 有一个属性为 next
然后有一个 LinkedList 类
- 有一个属性为 headNode (类型是我们创建的 Node), 这个头节点不是用来存数据的,所以数据随便,重要的是他的 next 属性
- 加一个节点,用一个 Node temp 先存着当前头结点,然后循环 temp.next 直到等于 null,temp 一直更新,所以最后 temp 是最后一个节点,这个时候 temp.setNext (传进来的节点)
- 删除一个节点,同理,找到最后一个节点,让最后一个节点 = null
还有其他各种方法,有时候需要先判断一下当前 headNode 的 next 是不是 null, 是的话那就是空链表了
或者我们写的那些方法比如说加节点可能是按照每个节点里面数据内容而加的 (顺序), 那么就需要判断他们数据等等等。这就有可能导致把一个节点插入到一到一个位置
先把我们插入的节点的 next 指向应该在那个插入节点的前一个位置的节点 (我们从头节点一个一个过去然后找到的) 的 next 指向的那个节点 /null
再把应该在那个插入节点的前一个位置的节点的 next 设置为我们插入的节点
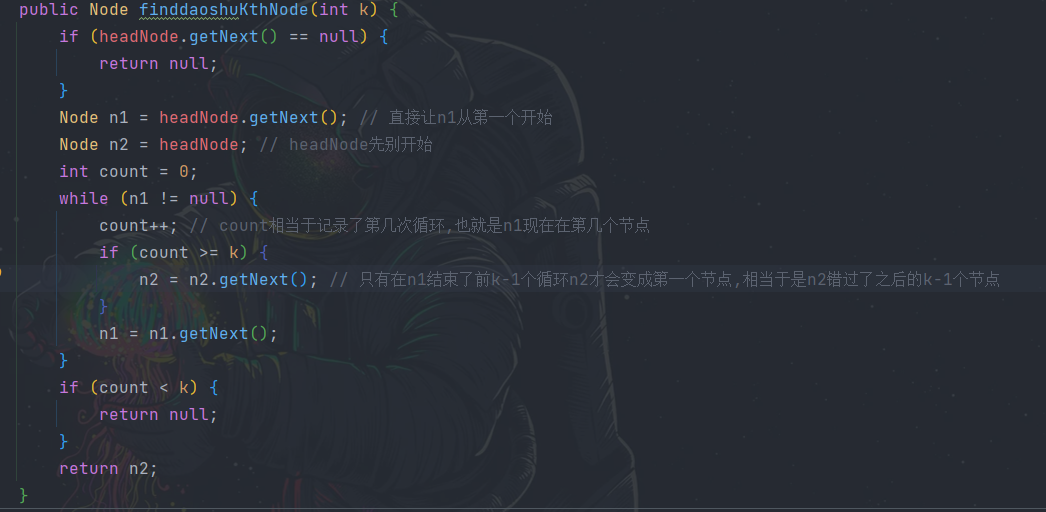
取出列表中倒数第 k 个节点
- 使用双指针!!!
- 然后判断链表是不是空的,是空的直接返回 null
- 先让 n1 指向 headNode, 再让 n2 指向 headNode
- 做个循环让 n1 走遍整个链表
其实传进来的那个 k 值,指的是倒数第几, 也可以说是除了最后 (k 值 - 1) 几个,让一个普通从前面开始遍历遍历到的位置
比如说一个链表有 10 个节点,想要他的倒数第三个节点 (k=3) 也就是他第 8 个节点, 这就相当于是让从第一个开始第 8 个就是了 (排除掉后面 k-1 个)
- 我们完全可以先声明一个变量 count 为 0, 然后拿一个指针 n1 正常从第一个节点 (也就是 headNode.getNext ()) 开始遍历,期间每次循环让 count+1
- 如果 count 在某次循环 + 1 后__等于或大于 k__, 那么证明当前这个指针 n1 正是第 k 个节点
- 此时同一个循环中让指针 n2 指向 n2.getNext (), 也就是第一个节点
- 让 n1 等于第 n 个节点,用来下次判断
- 因为 n2 是 n1 到了第 k 节点才开始的,等 n1 处理最后一个节点时,n2 会处理第 (链表的节点个数 -(k-1)) 个节点,也就是说相当于 n2 是比 n1 少了 k-1 个循环,而 n1 循环次数为链表的节点个数,n2 比 n1 少 k-1 个次数,他们两个都是从头开始的
- 也就是说最后 k-1 个节点没被 n2 reach 到,这跟倒数第 k 个节点意思一样,也就是 n2 就是倒数第 k 个节点
从第一个节点开始,一直到一个节点,然后之后 k-1 的节点不要去,这就是倒数第 k 个节点
注意还需各种其他的条件比如说传进来的 k 值比我们链表所有的节点总数还高那就应该返回 null
这是我的代码,只是一个很浅薄,易懂的实现方式
链表反转
头查法
- 新建一个链表 (或者新建一个节点代表头节点也可以)
- 遍历原来的链表把每一个节点放到新链表的最前端
- 也就是每次都是使用插入的方式都是插入
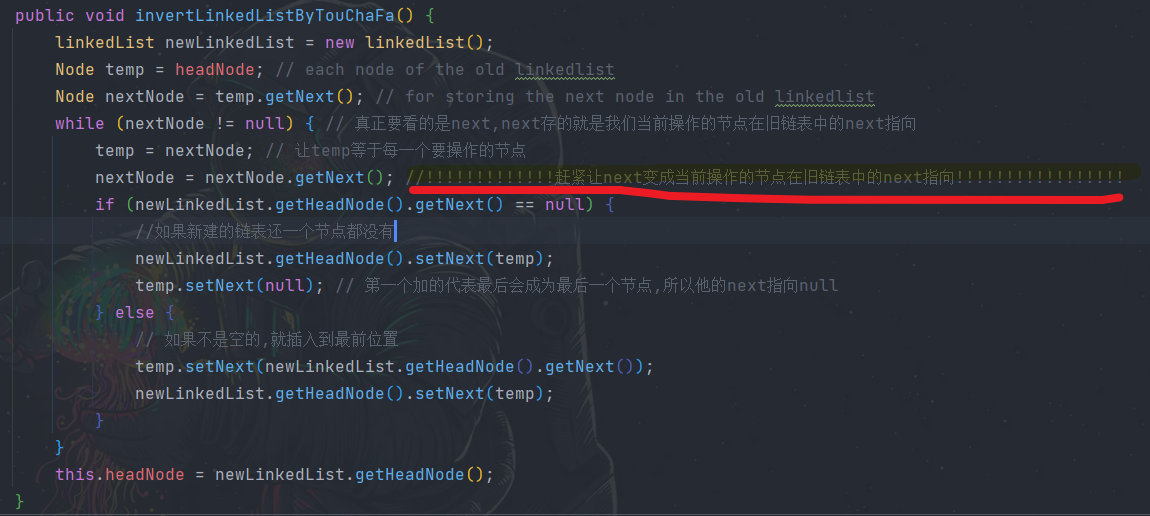
- 注意!!!遍历原来的链表里面的节点时, 需要先获得到每个节点的在原来链表的 next 指向的下一个节点或者 null 并把那个保存到一个变量,要是不这么做你直接把那个节点插入到新链表改变了这个节点的 next 指向,那么你就获取不了这个节点在原来链表的 next 指向的下一个节点或者是 null 了
- 最后等所有节点都插入到新的链表,再让旧链表的 headNode 的 next 指向新链表第一个节点
注意!每次循环都会操作一个旧链表中的节点,操作包括各种改他的 next 指向
所以要是之后再用那个节点调用 getNext 方法获取的 next__属性__指向不再是我们原来链表里面那个节点的 next__属性__指向了
所以我们需要在每次循环之前,先用 nextNode 变量存下当前被操作的节点在就旧链表中的 next__属性__指向,然后在对我们当前这个节点也就是 temp 各种操作,各种改这个节点的 next__属性__指向,我们的 nextNode 变量不会被影响,然后在下次循环时,只需让我们当前要操作的节点等于上一个循环 nextNode 变量变量存的值,也就是这一次循环我们要操作的节点 (上一次循环被操作的节点在旧链表中的 next__属性__指向的节点)
老师的方式 (也是头插法,更整洁)
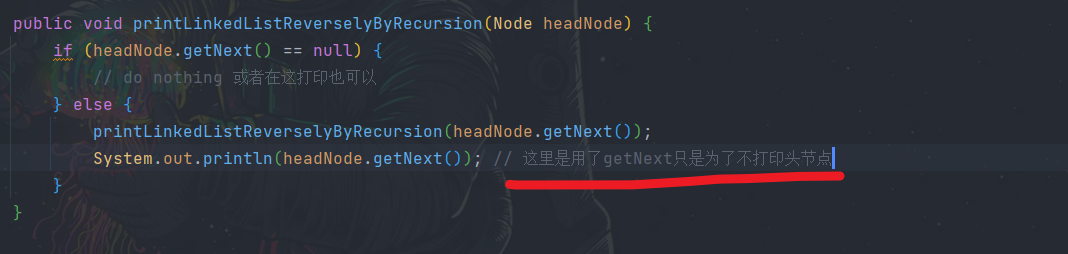
将一个链表中的节点逆序打印出来
递归方式:
参考上面逆转链表方式,反正就是逆转了然后打印
还可以使用栈数据结构
- 把每个节点压入栈
- 因为栈是先进后出
- 所以当把所有节点都存进去后再从上面一个一个取出来就是逆序的,取时可以打印就达成了逆序打印出来的效果
# 1.1、内存结构
- 内存上来看:链表存储空间不连续(不像数组)
# 1.2、逻辑结构
- 逻辑上来看:链表属于线性结构
# 1.3、链表特点
- 链表是以节点的方式来存储,是链式存储
- data 域存放数据,next 域指向下一个节点
- 链表分带头节点的链表和没有头节点的链表, 根据实际的需求来确定
# 2、链表应用场景
# 2.1、水浒英雄榜
- 使用带 head 头的单向链表实现【水浒英雄排行榜管理】
# 2.2、链表节点定义
- no :英雄编号
- name :英雄名字
- nickName :英雄昵称
- next :指向下一个 HeroNode 节点
//定义HeroNode , 每个HeroNode 对象就是一个节点
class HeroNode {
public int no;
public String name;
public String nickName;
public HeroNode next; // 指向下一个节点
// 构造器
public HeroNode(int no, String name, String nickname) {
this.no = no;
this.name = name;
this.nickName = nickname;
}
// 为了显示方法,我们重新toString
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + ", nickName=" + nickName + "]";
}
}# 2.3、链表定义
- DummyHead :头结点不存放数据,仅仅作为当前链表的入口
- head 字段的值不能改变,一旦改变,就丢失了整个链表的入口,我们也就无法通过 head 找到链表了
//定义SingleLinkedList 管理我们的英雄
class SingleLinkedList {
// 先初始化一个头节点, 头节点不要动, 不存放具体的数据
private HeroNode head = new HeroNode(0, "", "");
// 返回头节点
public HeroNode getHead() {
return head;
}
// ....# 2.4、遍历链表
# 2.4.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点
- 何时遍历完成?temp == null 表明当前节点为 null ,即表示已到链表末尾
- 如何遍历?temp = temp.next ,每次输出当前节点信息之后,temp 指针后移
# 2.4.2、代码实现
- 遍历链表
// 显示链表[遍历]
public void list() {
// 判断链表是否为空
if (head.next == null) {
System.out.println("链表为空");
return;
}
// 因为头节点,不能动,因此我们需要一个辅助变量来遍历
HeroNode temp = head.next;
while (true) {
// 判断是否到链表最后
if (temp == null) {
break;
}
// 输出节点的信息
System.out.println(temp);
// 将temp后移, 一定小心
temp = temp.next;
}
}# 2.5、尾部插入
# 2.5.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点
- 如何在链表末尾插入节点?
- 首先需要遍历链表,找到链表最后一个节点,当 temp.next == null 时,temp 节点指向链表最后一个节点
- 然后在 temp 节点之后插入节点即可:temp.next = heroNode
# 2.5.2、代码实现
- 在链表尾部插入节点
// 添加节点到单向链表
// 思路,当不考虑编号顺序时
// 1. 找到当前链表的最后节点
// 2. 将最后这个节点的next 指向 新的节点
public void add(HeroNode heroNode) {
// 因为head节点不能动,因此我们需要一个辅助遍历 temp
HeroNode temp = head;
// 遍历链表,找到最后
while (true) {
// 找到链表的最后
if (temp.next == null) {//
break;
}
// 如果没有找到最后, 将将temp后移
temp = temp.next;
}
// 当退出while循环时,temp就指向了链表的最后
// 将最后这个节点的next 指向 新的节点
temp.next = heroNode;
}- 测试代码
public static void main(String[] args) {
// 进行测试
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
// 创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
// 加入
singleLinkedList.add(hero1);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
singleLinkedList.add(hero4);
singleLinkedList.list();
}- 程序运行结果
HeroNode [no=1, name=宋江, nickName=及时雨]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=4, name=林冲, nickName=豹子头]# 2.6、按顺序插入
# 2.6.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点
- 应该如何执行插入?(待插入节点为 heroNode)
- 首先需要遍历链表,找到链表中编号值比 heroNode.no 大的节点,暂且叫它 biggerNode ,然后把 heroNode 插入到 biggerNode 之前即可
- 怎么找 biggerNode ?当 temp.next.no > heroNode.no 时,这时 temp.next 节点就是 biggerNode 节点。
- 为什么是 temp.next 节点?只有找到 temp 节点和 temp.next(biggerNode )节点,才能在 temp 节点和 temp.next 节点之间插入 heroNode 节点
- 怎么插入?
- heroNode .next = temp.next;
- temp.next = heroNode;
# 2.6.2、代码实现
- 按照英雄排名的顺序进行插入
// 第二种方式在添加英雄时,根据排名将英雄插入到指定位置
// (如果有这个排名,则添加失败,并给出提示)
public void addByOrder(HeroNode heroNode) {
// 因为头节点不能动,因此我们仍然通过一个辅助指针(变量)来帮助找到添加的位置
// 因为单链表,因为我们找的temp 是位于 添加位置的前一个节点,否则插入不了
HeroNode temp = head;
boolean flag = false; // flag标志添加的编号是否存在,默认为false
while (true) {
if (temp.next == null) {// 说明temp已经在链表的最后
break; //
}
if (temp.next.no > heroNode.no) { // 位置找到,就在temp的后面插入
break;
} else if (temp.next.no == heroNode.no) {// 说明希望添加的heroNode的编号已然存在
flag = true; // 说明编号存在
break;
}
temp = temp.next; // 后移,遍历当前链表
}
// 判断flag 的值
if (flag) { // 不能添加,说明编号存在
System.out.printf("准备插入的英雄的编号 %d 已经存在了, 不能加入\n", heroNode.no);
} else {
// 插入到链表中, temp的后面
heroNode.next = temp.next;
temp.next = heroNode;
}
}- 测试代码
public static void main(String[] args) {
// 进行测试
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
// 创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
// 加入按照编号的顺序
singleLinkedList.addByOrder(hero1);
singleLinkedList.addByOrder(hero4);
singleLinkedList.addByOrder(hero2);
singleLinkedList.addByOrder(hero3);
// 显示一把
singleLinkedList.list();
}- 程序运行结果
HeroNode [no=1, name=宋江, nickName=及时雨]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=4, name=林冲, nickName=豹子头]# 2.7、修改节点信息
# 2.7.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点
- 如何找到指定节点?temp.no = newHeroNode.no
# 2.7.2、代码实现
- 修改指定节点信息
`// 修改节点的信息, 根据no编号来修改,即no编号不能改.
// 说明
// 1. 根据 newHeroNode 的 no 来修改即可
public void update(HeroNode newHeroNode) {
// 判断是否空
if (head.next == null) {
System.out.println("链表为空~");
return;
}
// 找到需要修改的节点, 根据no编号
// 定义一个辅助变量
HeroNode temp = head.next;
boolean flag = false; // 表示是否找到该节点
while (true) {
if (temp == null) {
break; // 已经遍历完链表
}
if (temp.no == newHeroNode.no) {
// 找到
flag = true;
break;
}
temp = temp.next;
}
// 根据flag 判断是否找到要修改的节点
if (flag) {
temp.name = newHeroNode.name;
temp.nickName = newHeroNode.nickName;
} else { // 没有找到
System.out.printf("没有找到 编号 %d 的节点,不能修改\n", newHeroNode.no);
}
}- 测试代码
public static void main(String[] args) {
// 进行测试
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
// 创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
// 加入按照编号的顺序
singleLinkedList.addByOrder(hero1);
singleLinkedList.addByOrder(hero4);
singleLinkedList.addByOrder(hero2);
singleLinkedList.addByOrder(hero3);
// 测试修改节点的代码
HeroNode newHeroNode = new HeroNode(2, "小卢", "玉麒麟~~");
singleLinkedList.update(newHeroNode);
singleLinkedList.list();
}- 程序运行结果
HeroNode [no=1, name=宋江, nickName=及时雨]
HeroNode [no=2, name=小卢, nickName=玉麒麟~~]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=4, name=林冲, nickName=豹子头]# 2.8、删除节点
# 2.8.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点
- 如何找到待删除的节点?遍历链表,当 temp.next == no 时,temp.next 节点就是待删除的节点
- 如何删除?temp = temp.next.next 即可删除 temp.next 节点,该节点没有引用指向它,会被垃圾回收机制回收
# 2.8.2、代码实现
- 删除指定节点
// 删除节点
// 思路
// 1. head 不能动,因此我们需要一个temp辅助节点找到待删除节点的前一个节点
// 2. 说明我们在比较时,是temp.next.no 和 需要删除的节点的no比较
public void del(int no) {
HeroNode temp = head;
boolean flag = false; // 标志是否找到待删除节点的
while (true) {
if (temp.next == null) { // 已经到链表的最后
break;
}
if (temp.next.no == no) {
// 找到的待删除节点的前一个节点temp
flag = true;
break;
}
temp = temp.next; // temp后移,遍历
}
// 判断flag
if (flag) { // 找到
// 可以删除
temp.next = temp.next.next;
} else {
System.out.printf("要删除的 %d 节点不存在\n", no);
}
}- 测试代码
public static void main(String[] args) {
// 进行测试
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
// 创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
// 加入
singleLinkedList.add(hero1);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
singleLinkedList.add(hero4);
// 删除节点
singleLinkedList.del(1);
singleLinkedList.del(4);
singleLinkedList.list();
}- 程序运行结果
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=3, name=吴用, nickName=智多星]# 2.9、总结
- 遍历链表,执行操作时,判断条件有时候是 temp ,有时候是 temp.next ,Why?
- 对于插入、删除节点来说,需要知道当前待操作的节点(heroNode)前一个节点的地址(指针),如果直接定位至当前待操作的节点 heroNode ,那没得玩。。。因为不知道 heroNode 前一个节点的地址,无法进行插入、删除操作,所以 while 循环中的条件使用 temp.next 进行判断
- 对于更新、遍历操作来说,我需要的仅仅就只是当前节点的信息,所以 while 循环中的条件使用 temp 进行判断
- 头结点与首节点
- 参考资料:https://blog.csdn.net/WYpersist/article/details/80288056
- 头结点是为了操作的统一与方便而设立的,放在第一个元素结点之前,其数据域一般无意义(当然有些情况下也可存放链表的长度、用做监视哨等等)。
- 首元结点也就是第一个元素的结点,它是头结点后边的第一个结点。
# 3、单链表面试题
# 3.1、求单链表中有效节点的个数
# 3.1.1、代码思路
- 求单链表中有效节点的个数:遍历即可
# 3.1.2、代码实现
- 求单链表中有效节点的个数
// 方法:获取到单链表的节点的个数(如果是带头结点的链表,需求不统计头节点)
/**
*
* @param head 链表的头节点
* @return 返回的就是有效节点的个数
*/
public static int getLength(HeroNode head) {
if (head.next == null) { // 空链表
return 0;
}
int length = 0;
// 定义一个辅助的变量, 这里我们没有统计头节点
HeroNode cur = head.next;
while (cur != null) {
length++;
cur = cur.next; // 遍历
}
return length;
}- 测试代码
public static void main(String[] args) {
// 进行测试
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
// 创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
// 加入
singleLinkedList.add(hero1);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
singleLinkedList.add(hero4);
singleLinkedList.list();
// 测试一下 求单链表中有效节点的个数
System.out.println("有效的节点个数=" + getLength(singleLinkedList.getHead()));// 2
}- 程序运行结果
HeroNode [no=1, name=宋江, nickName=及时雨]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=4, name=林冲, nickName=豹子头]
有效的节点个数=4
# 3.2、查找单链表中的倒数第 k 个结点
# 3.2.1、代码思路
- 查找单链表中的倒数第 k 个结点 【新浪面试题】
- 首先,获取整个链表中元素的个数 size
- 在使用 for 循环定位至倒数第 index(形参) 个节点,返回即可
- for 循环的条件应如何确定?for (int i = 0; i < x; i++) 中 x 的值应是多少?我们需要定位至倒数第 index 个节点,在 for 循环之前,我们已经定位置首节点,还需再走 (size - index ) 步,定位至倒数第 index 个节点
- 举例说明:链表中一共有 4 个元素,想要定位至倒数第 2 个节点,那么需要在首节点之后走两步,到达倒数第 2 个节点
# 3.2.2、代码实现
- 查找单链表中的倒数第 k 个结点
// 查找单链表中的倒数第k个结点 【新浪面试题】
// 思路
// 1. 编写一个方法,接收head节点,同时接收一个index
// 2. index 表示是倒数第index个节点
// 3. 先把链表从头到尾遍历,得到链表的总的长度 getLength
// 4. 得到size 后,我们从链表的第一个开始遍历 (size-index)个,就可以得到
// 5. 如果找到了,则返回该节点,否则返回nulll
public static HeroNode findLastIndexNode(HeroNode head, int index) {
// 判断如果链表为空,返回null
if (head.next == null) {
return null;// 没有找到
}
// 第一个遍历得到链表的长度(节点个数)
int size = getLength(head);
// 第二次遍历 size-index 位置,就是我们倒数的第K个节点
// 先做一个index的校验
if (index <= 0 || index > size) {
return null;
}
// 定义给辅助变量, for 循环定位到倒数的index
HeroNode cur = head.next; // 3 // 3 - 1 = 2
for (int i = 0; i < size - index; i++) {
cur = cur.next;
}
return cur;
}
- 测试代码
public static void main(String[] args) {
// 进行测试
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
// 创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
// 加入
singleLinkedList.add(hero1);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
singleLinkedList.add(hero4);
singleLinkedList.list();
// 测试一下看看是否得到了倒数第K个节点
HeroNode res = findLastIndexNode(singleLinkedList.getHead(), 2);
System.out.println("res=" + res);
}
- 程序运行结果
HeroNode [no=1, name=宋江, nickName=及时雨]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=4, name=林冲, nickName=豹子头]
res=HeroNode [no=3, name=吴用, nickName=智多星]# 3.3、单链表的反转
# 3.3.1、代码思路
- 单链表的反转【腾讯面试题,有点难度】
- 定义一个新的头结点 reverseHead ,一点一点将链表反转后,再串起来
- 怎么个串法?
- 在原链表中每读取一个节点(cur),先保存其下一个节点的地址(next),然后将 cur 节点放在新链表的最前面
- 然后执行遍历:cur = next ,即指针后移
- 遍历完成后,新链表即是反转后的链表
- 如何将 cur 节点插入在新链表的最前面
- cur.next = reverseHead.next;
- reverseHead.next = cur;
- while 循环终止条件? cur == null :已遍历至链表尾部
- 单链表的翻转可以参考我的这篇博文:https://blog.csdn.net/oneby1314/article/details/107577923
# 3.3.2、代码实现
- 单链表的反转
// 将单链表反转
public static void reversetList(HeroNode head) {
// 如果当前链表为空,或者只有一个节点,无需反转,直接返回
if (head.next == null || head.next.next == null) {
return;
}
// 定义一个辅助的指针(变量),帮助我们遍历原来的链表
HeroNode cur = head.next;
HeroNode next = null;// 指向当前节点[cur]的下一个节点
HeroNode reverseHead = new HeroNode(0, "", "");
// 遍历原来的链表,每遍历一个节点,就将其取出,并放在新的链表reverseHead 的最前端
// 动脑筋
while (cur != null) {
next = cur.next;// 先暂时保存当前节点的下一个节点,因为后面需要使用
cur.next = reverseHead.next;// 将cur的下一个节点指向新的链表的最前端
reverseHead.next = cur; // 将cur 连接到新的链表上
cur = next;// 让cur后移
}
// 将head.next 指向 reverseHead.next , 实现单链表的反转
head.next = reverseHead.next;
}- 测试代码
public static void main(String[] args) {
// 进行测试
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
// 创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
// 加入
singleLinkedList.add(hero1);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
singleLinkedList.add(hero4);
// 测试一下单链表的反转功能
System.out.println("原来链表的情况~~");
singleLinkedList.list();
System.out.println("反转单链表~~");
reversetList(singleLinkedList.getHead());
singleLinkedList.list();
}
- 程序运行结果
原来链表的情况~~
HeroNode [no=1, name=宋江, nickName=及时雨]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=4, name=林冲, nickName=豹子头]
反转单链表~~
HeroNode [no=4, name=林冲, nickName=豹子头]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=1, name=宋江, nickName=及时雨]# 3.4、单链表的反转(我的代码)
# 3.4.1、代码思路
- 单链表的反转【腾讯面试题,有点难度】
- 原链表为 cur 指向 next ,反转链表不就是把 next 指向 cur 吗?
- 由于 next 指向 cur 时,next 将丢失其下一节点的地址,所以需要先将 nnext 保存起来
- next ==null 时链表已经反转完毕,最后将头结点指向 cur 节点即可
# 3.4.2、代码实现
- 单链表的反转
// 将单链表反转
public static void myReversetList(HeroNode head) {
// 如果当前链表为空,或者只有一个节点,无需反转,直接返回
if (head.next == null || head.next.next == null) {
return;
}
// 当前节点
HeroNode cur = head.next;
// 下一节点
HeroNode next = cur.next;
// 首节点反转后为尾节点,需指向 null
cur.next = null;
// next == null 时,链表已经反转完毕
while (next != null) {
// 记录 next 的后一节点
HeroNode nnext = next.next;
// 反转链表
next.next = cur;
// 指针后移
cur = next;
next = nnext;
}
// 最后加上首节点
head.next = cur;
}- 测试代码
public static void main(String[] args) {
// 进行测试
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
// 创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
// 加入
singleLinkedList.add(hero1);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
singleLinkedList.add(hero4);
// 测试一下单链表的反转功能
System.out.println("原来链表的情况~~");
singleLinkedList.list();
System.out.println("反转单链表~~");
reversetList(singleLinkedList.getHead());
singleLinkedList.list();
}- 程序运行结果
原来链表的情况~~
HeroNode [no=1, name=宋江, nickName=及时雨]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=4, name=林冲, nickName=豹子头]
反转单链表~~
HeroNode [no=4, name=林冲, nickName=豹子头]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=1, name=宋江, nickName=及时雨]# 3.5、从尾到头打印单链表
# 3.5.1、栈的基本使用
- 测试代码
public static void main(String[] args) {
Stack<String> stack = new Stack();
// 入栈
stack.add("jack");
stack.add("tom");
stack.add("smith");
// 出栈
// smith, tom , jack
while (stack.size() > 0) {
System.out.println(stack.pop());//pop就是将栈顶的数据取出
}
}- 程序运行结果
smith
tom
jack# 3.5.2、代码思路
- 从尾到头打印单链表 【百度,要求方式 1:反向遍历 。 方式 2:Stack 栈】
- 方式一:先将单链表进行反转操作,然后再遍历输出,问题:破坏原链表结构,不可取
- 方式二:遍历链表,去除节点压入栈中,利用栈先进后出的特点,实现逆序打印
# 3.5.3、代码实现
- 从尾到头打印单链表
// 方式2:
// 可以利用栈这个数据结构,将各个节点压入到栈中,然后利用栈的先进后出的特点,就实现了逆序打印的效果
public static void reversePrint(HeroNode head) {
if (head.next == null) {
return;// 空链表,不能打印
}
// 创建要给一个栈,将各个节点压入栈
Stack<HeroNode> stack = new Stack<HeroNode>();
HeroNode cur = head.next;
// 将链表的所有节点压入栈
while (cur != null) {
stack.push(cur);
cur = cur.next; // cur后移,这样就可以压入下一个节点
}
// 将栈中的节点进行打印,pop 出栈
while (stack.size() > 0) {
System.out.println(stack.pop()); // stack的特点是先进后出
}
}
- 测试代码
public static void main(String[] args) {
//进行测试
//先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
//创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
//加入
singleLinkedList.add(hero1);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
singleLinkedList.add(hero4);
System.out.println("原来链表的情况~~");
singleLinkedList.list();
System.out.println("测试逆序打印单链表, 没有改变链表的结构~~");
reversePrint(singleLinkedList.getHead());
}- 程序运行结果
原来链表的情况~~
HeroNode [no=1, name=宋江, nickName=及时雨]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=4, name=林冲, nickName=豹子头]
测试逆序打印单链表, 没有改变链表的结构~~
HeroNode [no=4, name=林冲, nickName=豹子头]
HeroNode [no=3, name=吴用, nickName=智多星]
HeroNode [no=2, name=卢俊义, nickName=玉麒麟]
HeroNode [no=1, name=宋江, nickName=及时雨]# 3.6、合并两个有序的单链表
# 3.6.1、代码思路
- 合并两个有序的单链表,合并之后的链表依然有序【课后练习】
# 3.6.2、代码实现
- 合并两个有序的单链表,合并之后的链表依然有序
- 具体讲解见我的一篇博客:https://blog.csdn.net/oneby1314/article/details/107590876
# 3.7、单向链表所有代码
public class SingleLinkedListDemo {
public static void main(String[] args) {
//进行测试
//先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");
//创建要给链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
//加入
singleLinkedList.add(hero1);
singleLinkedList.add(hero4);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);
// 测试一下单链表的反转功能
System.out.println("原来链表的情况~~");
singleLinkedList.list();
System.out.println("反转单链表~~");
reversetList(singleLinkedList.getHead());
singleLinkedList.list();
System.out.println("测试逆序打印单链表, 没有改变链表的结构~~");
reversePrint(singleLinkedList.getHead());
//加入按照编号的顺序
singleLinkedList.addByOrder(hero1);
singleLinkedList.addByOrder(hero4);
singleLinkedList.addByOrder(hero2);
singleLinkedList.addByOrder(hero3);
//显示一把
singleLinkedList.list();
//测试修改节点的代码
HeroNode newHeroNode = new HeroNode(2, "小卢", "玉麒麟~~");
singleLinkedList.update(newHeroNode);
System.out.println("修改后的链表情况~~");
singleLinkedList.list();
//删除一个节点
singleLinkedList.del(1);
singleLinkedList.del(4);
System.out.println("删除后的链表情况~~");
singleLinkedList.list();
//测试一下 求单链表中有效节点的个数
System.out.println("有效的节点个数=" + getLength(singleLinkedList.getHead()));//2
//测试一下看看是否得到了倒数第K个节点
HeroNode res = findLastIndexNode(singleLinkedList.getHead(), 3);
System.out.println("res=" + res);
}
// 方式2:
// 可以利用栈这个数据结构,将各个节点压入到栈中,然后利用栈的先进后出的特点,就实现了逆序打印的效果
public static void reversePrint(HeroNode head) {
if (head.next == null) {
return;// 空链表,不能打印
}
// 创建要给一个栈,将各个节点压入栈
Stack<HeroNode> stack = new Stack<HeroNode>();
HeroNode cur = head.next;
// 将链表的所有节点压入栈
while (cur != null) {
stack.push(cur);
cur = cur.next; // cur后移,这样就可以压入下一个节点
}
// 将栈中的节点进行打印,pop 出栈
while (stack.size() > 0) {
System.out.println(stack.pop()); // stack的特点是先进后出
}
}
// 将单链表反转
public static void reversetList(HeroNode head) {
// 如果当前链表为空,或者只有一个节点,无需反转,直接返回
if (head.next == null || head.next.next == null) {
return;
}
// 定义一个辅助的指针(变量),帮助我们遍历原来的链表
HeroNode cur = head.next;
HeroNode next = null;// 指向当前节点[cur]的下一个节点
HeroNode reverseHead = new HeroNode(0, "", "");
// 遍历原来的链表,每遍历一个节点,就将其取出,并放在新的链表reverseHead 的最前端
// 动脑筋
while (cur != null) {
next = cur.next;// 先暂时保存当前节点的下一个节点,因为后面需要使用
cur.next = reverseHead.next;// 将cur的下一个节点指向新的链表的最前端
reverseHead.next = cur; // 将cur 连接到新的链表上
cur = next;// 让cur后移
}
// 将head.next 指向 reverseHead.next , 实现单链表的反转
head.next = reverseHead.next;
}
// 将单链表反转
public static void myReversetList(HeroNode head) {
// 如果当前链表为空,或者只有一个节点,无需反转,直接返回
if (head.next == null || head.next.next == null) {
return;
}
// 当前节点
HeroNode cur = head.next;
// 下一节点
HeroNode next = cur.next;
// 首节点反转后为尾节点,需指向 null
cur.next = null;
// next == null 时,链表已经反转完毕
while (next != null) {
// 记录 next 的后一节点
HeroNode nnext = next.next;
// 反转链表
next.next = cur;
// 指针后移
cur = next;
next = nnext;
}
// 最后加上头结点
head.next = cur;
}
// 查找单链表中的倒数第k个结点 【新浪面试题】
// 思路
// 1. 编写一个方法,接收head节点,同时接收一个index
// 2. index 表示是倒数第index个节点
// 3. 先把链表从头到尾遍历,得到链表的总的长度 getLength
// 4. 得到size 后,我们从链表的第一个开始遍历 (size-index)个,就可以得到
// 5. 如果找到了,则返回该节点,否则返回nulll
public static HeroNode findLastIndexNode(HeroNode head, int index) {
// 判断如果链表为空,返回null
if (head.next == null) {
return null;// 没有找到
}
// 第一个遍历得到链表的长度(节点个数)
int size = getLength(head);
// 第二次遍历 size-index 位置,就是我们倒数的第K个节点
// 先做一个index的校验
if (index <= 0 || index > size) {
return null;
}
// 定义给辅助变量, for 循环定位到倒数的index
HeroNode cur = head.next; // 3 // 3 - 1 = 2
for (int i = 0; i < size - index; i++) {
cur = cur.next;
}
return cur;
}
// 方法:获取到单链表的节点的个数(如果是带头结点的链表,需求不统计头节点)
/**
*
* @param head 链表的头节点
* @return 返回的就是有效节点的个数
*/
public static int getLength(HeroNode head) {
if (head.next == null) { // 空链表
return 0;
}
int length = 0;
// 定义一个辅助的变量, 这里我们没有统计头节点
HeroNode cur = head.next;
while (cur != null) {
length++;
cur = cur.next; // 遍历
}
return length;
}
}
//定义SingleLinkedList 管理我们的英雄
class SingleLinkedList {
// 先初始化一个头节点, 头节点不要动, 不存放具体的数据
private HeroNode head = new HeroNode(0, "", "");
// 返回头节点
public HeroNode getHead() {
return head;
}
// 添加节点到单向链表
// 思路,当不考虑编号顺序时
// 1. 找到当前链表的最后节点
// 2. 将最后这个节点的next 指向 新的节点
public void add(HeroNode heroNode) {
// 因为head节点不能动,因此我们需要一个辅助遍历 temp
HeroNode temp = head;
// 遍历链表,找到最后
while (true) {
// 找到链表的最后
if (temp.next == null) {//
break;
}
// 如果没有找到最后, 将将temp后移
temp = temp.next;
}
// 当退出while循环时,temp就指向了链表的最后
// 将最后这个节点的next 指向 新的节点
temp.next = heroNode;
}
// 第二种方式在添加英雄时,根据排名将英雄插入到指定位置
// (如果有这个排名,则添加失败,并给出提示)
public void addByOrder(HeroNode heroNode) {
// 因为头节点不能动,因此我们仍然通过一个辅助指针(变量)来帮助找到添加的位置
// 因为单链表,因为我们找的temp 是位于 添加位置的前一个节点,否则插入不了
HeroNode temp = head;
boolean flag = false; // flag标志添加的编号是否存在,默认为false
while (true) {
if (temp.next == null) {// 说明temp已经在链表的最后
break; //
}
if (temp.next.no > heroNode.no) { // 位置找到,就在temp的后面插入
break;
} else if (temp.next.no == heroNode.no) {// 说明希望添加的heroNode的编号已然存在
flag = true; // 说明编号存在
break;
}
temp = temp.next; // 后移,遍历当前链表
}
// 判断flag 的值
if (flag) { // 不能添加,说明编号存在
System.out.printf("准备插入的英雄的编号 %d 已经存在了, 不能加入\n", heroNode.no);
} else {
// 插入到链表中, temp的后面
heroNode.next = temp.next;
temp.next = heroNode;
}
}
// 修改节点的信息, 根据no编号来修改,即no编号不能改.
// 说明
// 1. 根据 newHeroNode 的 no 来修改即可
public void update(HeroNode newHeroNode) {
// 判断是否空
if (head.next == null) {
System.out.println("链表为空~");
return;
}
// 找到需要修改的节点, 根据no编号
// 定义一个辅助变量
HeroNode temp = head.next;
boolean flag = false; // 表示是否找到该节点
while (true) {
if (temp == null) {
break; // 已经遍历完链表
}
if (temp.no == newHeroNode.no) {
// 找到
flag = true;
break;
}
temp = temp.next;
}
// 根据flag 判断是否找到要修改的节点
if (flag) {
temp.name = newHeroNode.name;
temp.nickName = newHeroNode.nickName;
} else { // 没有找到
System.out.printf("没有找到 编号 %d 的节点,不能修改\n", newHeroNode.no);
}
}
// 删除节点
// 思路
// 1. head 不能动,因此我们需要一个temp辅助节点找到待删除节点的前一个节点
// 2. 说明我们在比较时,是temp.next.no 和 需要删除的节点的no比较
public void del(int no) {
HeroNode temp = head;
boolean flag = false; // 标志是否找到待删除节点的
while (true) {
if (temp.next == null) { // 已经到链表的最后
break;
}
if (temp.next.no == no) {
// 找到的待删除节点的前一个节点temp
flag = true;
break;
}
temp = temp.next; // temp后移,遍历
}
// 判断flag
if (flag) { // 找到
// 可以删除
temp.next = temp.next.next;
} else {
System.out.printf("要删除的 %d 节点不存在\n", no);
}
}
// 显示链表[遍历]
public void list() {
// 判断链表是否为空
if (head.next == null) {
System.out.println("链表为空");
return;
}
// 因为头节点,不能动,因此我们需要一个辅助变量来遍历
HeroNode temp = head.next;
while (true) {
// 判断是否到链表最后
if (temp == null) {
break;
}
// 输出节点的信息
System.out.println(temp);
// 将temp后移, 一定小心
temp = temp.next;
}
}
}
//定义HeroNode , 每个HeroNode 对象就是一个节点
class HeroNode {
public int no;
public String name;
public String nickName;
public HeroNode next; // 指向下一个节点
// 构造器
public HeroNode(int no, String name, String nickname) {
this.no = no;
this.name = name;
this.nickName = nickname;
}
// 为了显示方法,我们重新toString
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + ", nickName=" + nickName + "]";
}
}# 4、双向链表
- 双向链表删除一个节点只需要那个节点就行了,不像单向链表一样必须需要要删除的那个节点的前一个节点和当前被删除的节点
- 双向链表的每一个节点有着 data 属性,next 属性,和 prev 属性 (这个 prev 指的是当前节点的上一个节点)
遍历:
- 可以向后遍历,也可以像前遍历
添加:
- 找到最后节点把添加的节点的 prev 设为这个最后的节点然后把这个最后的节点的 next 设置为添加的节点
删除:
- 找到要删的节点
- 那个节点.prev.next = 那个节点.next
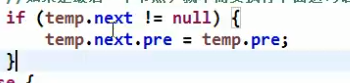
- 那个节点.next.prev = 那个节点.prev (_注意这个有风险!!!因为要删除的节点可能是最后的节点,说明他的 next 可能会是 null, 所以需要判断_)
# 4.1、与单向链表的比较
- 单向链表, 查找的方向只能是一个方向, 而双向链表可以向前或者向后查找
- 单向链表不能自我删除, 需要靠辅助节点 , 而双向链表, 则可以自我删除, 所以前面我们单链表删除时节点, 总是找到 temp ,temp 是待删除节点的前一个节点 (认真体会)
# 4.2、链表节点定义
- 在单向链表节点的基础上,增加 pre ,用于指向前一个节点
// 定义HeroNode , 每个HeroNode 对象就是一个节点
class HeroNode {
public int no;
public String name;
public String nickname;
public HeroNode next; // 指向下一个节点, 默认为null
public HeroNode pre; // 指向前一个节点, 默认为null
// 构造器
public HeroNode(int no, String name, String nickname) {
this.no = no;
this.name = name;
this.nickname = nickname;
}
// 为了显示方法,我们重新toString
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + ", nickname=" + nickname + "]";
}
}# 4.3、链表定义
- 定义整个链表的头结点,作为链表的入口
// 创建一个双向链表的类
class DoubleLinkedList {
// 先初始化一个头节点, 头节点不要动, 不存放具体的数据
private HeroNode head = new HeroNode(0, "", "");
// 返回头节点
public HeroNode getHead() {
return head;
}
// ...# 4.4、链表遍历
# 4.4.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点 ,用于遍历链表
- 何时停止 while 循环?temp == null :已经遍历至链表尾部
# 4.4.2、代码实现
// 遍历双向链表的方法
// 显示链表[遍历]
public void list() {
// 判断链表是否为空
if (head.next == null) {
System.out.println("链表为空");
return;
}
// 因为头节点,不能动,因此我们需要一个辅助变量来遍历
HeroNode temp = head.next;
while (true) {
// 判断是否到链表最后
if (temp == null) {
break;
}
// 输出节点的信息
System.out.println(temp);
// 将temp后移, 一定小心
temp = temp.next;
}
}# 4.5、尾部插入
# 4.5.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点
- 何时停止 while 循环?temp.next == null :temp 节点已经是链表最后一个节点,在 temp 节点之后插入 heroNode 节点即可
- 如何插入?
- temp.next 指向新的尾节点 heroNode :temp.next = heroNode;
- heroNode .pre 指向旧的尾节点 temp :heroNode.pre = temp;
# 4.5.2、代码实现
- 在链表尾部插入节点
// 添加一个节点到双向链表的最后.
public void add(HeroNode heroNode) {
// 因为head节点不能动,因此我们需要一个辅助遍历 temp
HeroNode temp = head;
// 遍历链表,找到最后
while (true) {
// 找到链表的最后
if (temp.next == null) {//
break;
}
// 如果没有找到最后, 将将temp后移
temp = temp.next;
}
// 当退出while循环时,temp就指向了链表的最后
// 形成一个双向链表
temp.next = heroNode;
heroNode.pre = temp;
}# 4.6、按顺序插入
# 4.6.1、代码思路
-
定义辅助变量 temp ,相当于一个指针,指向当前节点
-
我们将 heroNode 节点插入到 temp 节点之后还是 temp 节点之前?
- 如果插入到 temp 节点之后:
- 判断条件:temp.next.no > heroNode.no ,即 temp 的下一个节点的值比 heroNode 节点的值大,所以需要将 heroNode 插入到 temp 节点之后
- while 循环终止条件:
- temp.next == null :temp 节点已经是链表的尾节点
- temp.next.no > heroNode.no :heroNode 节点的值介于 temp 节点的值和 temp 下一个节点的值之间
- temp.next.no == heroNode.no :heroNode 节点的值等于 temp 下一个节点的值,不能进行插入
- 如果插入到 temp 节点之前:
- 判断条件:temp.no > heroNode.no ,即 temp 节点的值比 heroNode 节点的值大,所以需要将 heroNode 插入到 temp 节点之前
- 存在的问题:如果需要在链表尾部插入 heroNode 节点,即需要在 null 节点之前插入 heroNode 节点,定位至 null 节点将丢失其前一个节点的信息(除非使用一个变量保存起来),所以跳出循环的判断条件为:temp.next == null
- 所以我们选取:【插入到 temp 节点之后】方案
- 如果插入到 temp 节点之后:
# 4.6.2、代码实现
- 代码
// 第二种方式在添加英雄时,根据排名将英雄插入到指定位置
// (如果有这个排名,则添加失败,并给出提示)
public void addByOrder(HeroNode heroNode) {
// 因为头节点不能动,因此我们仍然通过一个辅助指针(变量)来帮助找到添加的位置
// 目标:在 temp 的后面插入节点
HeroNode temp = head;
boolean flag = false; // flag标志添加的编号是否存在,默认为false
while (true) {
if (temp.next == null) {// 说明temp已经在链表的最后
break;
}
if (temp.next.no > heroNode.no) { // 位置找到,就在temp的后面插入
break;
} else if (temp.next.no == heroNode.no) {// 说明希望添加的heroNode的编号已然存在
flag = true; // 说明编号存在
break;
}
temp = temp.next; // 后移,遍历当前链表
}
// 判断flag 的值
if (flag) { // 不能添加,说明编号存在
System.out.printf("准备插入的英雄的编号 %d 已经存在了, 不能加入\n", heroNode.no);
} else {
// 插入到链表中, temp的后面
// heroNode 指向 temp 节点的下一个节点
heroNode.next = temp.next;
if(temp.next != null) {
temp.next.pre = heroNode;
}
// temp 节点指向 heroNode 节点
temp.next = heroNode;
heroNode.pre = temp;
}
}# 4.7、修改节点信息
# 4.7.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点
- 如何找到指定节点?temp.no == no
# 4.7.2、代码实现
- 修改指定节点的信息
// 修改一个节点的内容, 可以看到双向链表的节点内容修改和单向链表一样
// 只是 节点类型改成 HeroNode2
public void update(HeroNode newHeroNode) {
// 判断是否空
if (head.next == null) {
System.out.println("链表为空~");
return;
}
// 找到需要修改的节点, 根据no编号
// 定义一个辅助变量
HeroNode temp = head.next;
boolean flag = false; // 表示是否找到该节点
while (true) {
if (temp == null) {
break; // 已经遍历完链表
}
if (temp.no == newHeroNode.no) {
// 找到
flag = true;
break;
}
temp = temp.next;
}
// 根据flag 判断是否找到要修改的节点
if (flag) {
temp.name = newHeroNode.name;
temp.nickname = newHeroNode.nickname;
} else { // 没有找到
System.out.printf("没有找到 编号 %d 的节点,不能修改\n", newHeroNode.no);
}
}# 4.8、删除节点
# 4.8.1、代码思路
- 定义辅助变量 temp ,相当于一个指针,指向当前节点
- while 循环的终止条件?由于 temp 节点就是待删除节点,所以终止条件是:temp == null
- 为何双向链表,可以实现自我删除?定位至待删除的节点 temp ,由于 temp 节点有其前一个节点和后一个节点的信息,所以可实现自我删除
- 如何删除?
- temp 的前一个节点的 next 域指向 temp 的后一个节点:temp.pre.next = temp.next;
- temp 的后一个节点的 pre 域指向 temp 的前一个节点:temp.next.pre = temp.pre;
- 有个地方需要注意,如果 temp 已经是链表尾节点,temp 已经没有下一个节点
- 这时只需要将 temp 的前一个节点的 next 指向 null 即可
- 所以 temp.next.pre = temp.pre; 执行的前提条件是 temp.next != null
# 4.8.2、代码实现
- 删除指定节点
// 从双向链表中删除一个节点,
// 说明
// 1 对于双向链表,我们可以直接找到要删除的这个节点
// 2 找到后,自我删除即可
public void del(int no) {
// 判断当前链表是否为空
if (head.next == null) {// 空链表
System.out.println("链表为空,无法删除");
return;
}
HeroNode temp = head.next; // 辅助变量(指针)
boolean flag = false; // 标志是否找到待删除节点的
while (true) {
if (temp == null) { // 已经到链表的最后
break;
}
if (temp.no == no) {
// 找到的待删除节点的前一个节点temp
flag = true;
break;
}
temp = temp.next; // temp后移,遍历
}
// 判断flag
if (flag) { // 找到
// 可以删除
// temp.next = temp.next.next;[单向链表]
temp.pre.next = temp.next;
// 这里我们的代码有问题?
// 如果是最后一个节点,就不需要执行下面这句话,否则出现空指针
if (temp.next != null) {
temp.next.pre = temp.pre;
}
} else {
System.out.printf("要删除的 %d 节点不存在\n", no);
}
}# 4.9、双向链表测试
# 4.9.1、测试代码
public static void main(String[] args) {
// 测试
System.out.println("双向链表的测试");
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(5, "林冲", "豹子头");
// 创建一个双向链表
DoubleLinkedList doubleLinkedList = new DoubleLinkedList();
doubleLinkedList.add(hero1);
doubleLinkedList.add(hero2);
doubleLinkedList.add(hero3);
doubleLinkedList.add(hero4);
doubleLinkedList.list();
// 测试按需插入
doubleLinkedList.addByOrder(new HeroNode(4, "Heygo", "Heygogo"));
doubleLinkedList.addByOrder(new HeroNode(6, "Oneby", "Onebyone"));
System.out.println("按顺序插入后的情况");
doubleLinkedList.list();
// 修改
HeroNode newHeroNode = new HeroNode(5, "公孙胜", "入云龙");
doubleLinkedList.update(newHeroNode);
System.out.println("修改后的链表情况");
doubleLinkedList.list();
// 删除
doubleLinkedList.del(3);
System.out.println("删除后的链表情况~~");
doubleLinkedList.list();
}# 4.9.2、程序运行结果
双向链表的测试
HeroNode [no=1, name=宋江, nickname=及时雨]
HeroNode [no=2, name=卢俊义, nickname=玉麒麟]
HeroNode [no=3, name=吴用, nickname=智多星]
HeroNode [no=5, name=林冲, nickname=豹子头]
按顺序插入后的情况
HeroNode [no=1, name=宋江, nickname=及时雨]
HeroNode [no=2, name=卢俊义, nickname=玉麒麟]
HeroNode [no=3, name=吴用, nickname=智多星]
HeroNode [no=4, name=Heygo, nickname=Heygogo]
HeroNode [no=5, name=林冲, nickname=豹子头]
HeroNode [no=6, name=Oneby, nickname=Onebyone]
修改后的链表情况
HeroNode [no=1, name=宋江, nickname=及时雨]
HeroNode [no=2, name=卢俊义, nickname=玉麒麟]
HeroNode [no=3, name=吴用, nickname=智多星]
HeroNode [no=4, name=Heygo, nickname=Heygogo]
HeroNode [no=5, name=公孙胜, nickname=入云龙]
HeroNode [no=6, name=Oneby, nickname=Onebyone]
删除后的链表情况~~
HeroNode [no=1, name=宋江, nickname=及时雨]
HeroNode [no=2, name=卢俊义, nickname=玉麒麟]
HeroNode [no=4, name=Heygo, nickname=Heygogo]
HeroNode [no=5, name=公孙胜, nickname=入云龙]
HeroNode [no=6, name=Oneby, nickname=Onebyone]# 4.10、双向链表所有代码
public class DoubleLinkedListDemo {
public static void main(String[] args) {
// 测试
System.out.println("双向链表的测试");
// 先创建节点
HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
HeroNode hero4 = new HeroNode(5, "林冲", "豹子头");
// 创建一个双向链表
DoubleLinkedList doubleLinkedList = new DoubleLinkedList();
doubleLinkedList.add(hero1);
doubleLinkedList.add(hero2);
doubleLinkedList.add(hero3);
doubleLinkedList.add(hero4);
doubleLinkedList.list();
// 测试按需插入
doubleLinkedList.addByOrder(new HeroNode(0, "Kobe", "BlackMamba"));
doubleLinkedList.addByOrder(new HeroNode(4, "Heygo", "Heygogo"));
doubleLinkedList.addByOrder(new HeroNode(6, "Oneby", "Onebyone"));
System.out.println("按顺序插入后的情况");
doubleLinkedList.list();
// 修改
HeroNode newHeroNode = new HeroNode(5, "公孙胜", "入云龙");
doubleLinkedList.update(newHeroNode);
System.out.println("修改后的链表情况");
doubleLinkedList.list();
// 删除
doubleLinkedList.del(3);
System.out.println("删除后的链表情况~~");
doubleLinkedList.list();
}
}
// 创建一个双向链表的类
class DoubleLinkedList {
// 先初始化一个头节点, 头节点不要动, 不存放具体的数据
private HeroNode head = new HeroNode(0, "", "");
// 返回头节点
public HeroNode getHead() {
return head;
}
// 遍历双向链表的方法
// 显示链表[遍历]
public void list() {
// 判断链表是否为空
if (head.next == null) {
System.out.println("链表为空");
return;
}
// 因为头节点,不能动,因此我们需要一个辅助变量来遍历
HeroNode temp = head.next;
while (true) {
// 判断是否到链表最后
if (temp == null) {
break;
}
// 输出节点的信息
System.out.println(temp);
// 将temp后移, 一定小心
temp = temp.next;
}
}
// 添加一个节点到双向链表的最后.
public void add(HeroNode heroNode) {
// 因为head节点不能动,因此我们需要一个辅助遍历 temp
HeroNode temp = head;
// 遍历链表,找到最后
while (true) {
// 找到链表的最后
if (temp.next == null) {//
break;
}
// 如果没有找到最后, 将将temp后移
temp = temp.next;
}
// 当退出while循环时,temp就指向了链表的最后
// 形成一个双向链表
temp.next = heroNode;
heroNode.pre = temp;
}
// 第二种方式在添加英雄时,根据排名将英雄插入到指定位置
// (如果有这个排名,则添加失败,并给出提示)
public void addByOrder(HeroNode heroNode) {
// 因为头节点不能动,因此我们仍然通过一个辅助指针(变量)来帮助找到添加的位置
// 目标:在 temp 的后面插入节点
HeroNode temp = head;
boolean flag = false; // flag标志添加的编号是否存在,默认为false
while (true) {
if (temp.next == null) {// 说明temp已经在链表的最后
break;
}
if (temp.next.no > heroNode.no) { // 位置找到,就在temp的后面插入
break;
} else if (temp.next.no == heroNode.no) {// 说明希望添加的heroNode的编号已然存在
flag = true; // 说明编号存在
break;
}
temp = temp.next; // 后移,遍历当前链表
}
// 判断flag 的值
if (flag) { // 不能添加,说明编号存在
System.out.printf("准备插入的英雄的编号 %d 已经存在了, 不能加入\n", heroNode.no);
} else {
// 插入到链表中, temp的后面
// heroNode 指向 temp 节点的下一个节点
heroNode.next = temp.next;
if(temp.next != null) {
temp.next.pre = heroNode;
}
// temp 节点指向 heroNode 节点
temp.next = heroNode;
heroNode.pre = temp;
}
}
// 修改一个节点的内容, 可以看到双向链表的节点内容修改和单向链表一样
// 只是 节点类型改成 HeroNode2
public void update(HeroNode newHeroNode) {
// 判断是否空
if (head.next == null) {
System.out.println("链表为空~");
return;
}
// 找到需要修改的节点, 根据no编号
// 定义一个辅助变量
HeroNode temp = head.next;
boolean flag = false; // 表示是否找到该节点
while (true) {
if (temp == null) {
break; // 已经遍历完链表
}
if (temp.no == newHeroNode.no) {
// 找到
flag = true;
break;
}
temp = temp.next;
}
// 根据flag 判断是否找到要修改的节点
if (flag) {
temp.name = newHeroNode.name;
temp.nickname = newHeroNode.nickname;
} else { // 没有找到
System.out.printf("没有找到 编号 %d 的节点,不能修改\n", newHeroNode.no);
}
}
// 从双向链表中删除一个节点,
// 说明
// 1 对于双向链表,我们可以直接找到要删除的这个节点
// 2 找到后,自我删除即可
public void del(int no) {
// 判断当前链表是否为空
if (head.next == null) {// 空链表
System.out.println("链表为空,无法删除");
return;
}
HeroNode temp = head.next; // 辅助变量(指针)
boolean flag = false; // 标志是否找到待删除节点的
while (true) {
if (temp == null) { // 已经到链表的最后
break;
}
if (temp.no == no) {
// 找到的待删除节点的前一个节点temp
flag = true;
break;
}
temp = temp.next; // temp后移,遍历
}
// 判断flag
if (flag) { // 找到
// 可以删除
// temp.next = temp.next.next;[单向链表]
temp.pre.next = temp.next;
// 这里我们的代码有问题?
// 如果是最后一个节点,就不需要执行下面这句话,否则出现空指针
if (temp.next != null) {
temp.next.pre = temp.pre;
}
} else {
System.out.printf("要删除的 %d 节点不存在\n", no);
}
}
}
// 定义HeroNode , 每个HeroNode 对象就是一个节点
class HeroNode {
public int no;
public String name;
public String nickname;
public HeroNode next; // 指向下一个节点, 默认为null
public HeroNode pre; // 指向前一个节点, 默认为null
// 构造器
public HeroNode(int no, String name, String nickname) {
this.no = no;
this.name = name;
this.nickname = nickname;
}
// 为了显示方法,我们重新toString
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + ", nickname=" + nickname + "]";
}
}# 4.11、总结
- 辅助变量 temp ,相当于一个指针,指向当前节点
- 如果定位至当前节点会丢失前一个节点的信息,那么我们只能定位至待操作节点的前一个节点:使用 temp.next 进行条件判断
# 5、单向环形链表
- 也就是一些节点,形成一个圆圈,每个 next 指向导致形成圆圈,就没有指向 null 的,也没有头结点 (可有可无)
- 有两个指针一个是 first 指向第一个添加到这个单向环形链表的,一个是 current 指向最后一个添加到这个单向环形链表的节点
添加节点
- 如果第一个节点,first 和 current 就指向这个节点,然后让这个节点的 next 指向他自己
- 再添加节点,让 current 存的那个节点的 next 指向当前添加的节点,然后当前添加的节点的 next 指向 first 也就是第一个节点
遍历这个环形链表
- 用一个辅助指针首先从 first 存的第一个节点开始
- 循环,直到辅助指针.next==first 就代表是最后一个了,已经走了一圈了
现在需要解决 Josephu 问题
- 就是你当前这个环形链表存的这些节点
- 用户给个数字比如说 2, 然后你就环形链表有 5 个节点
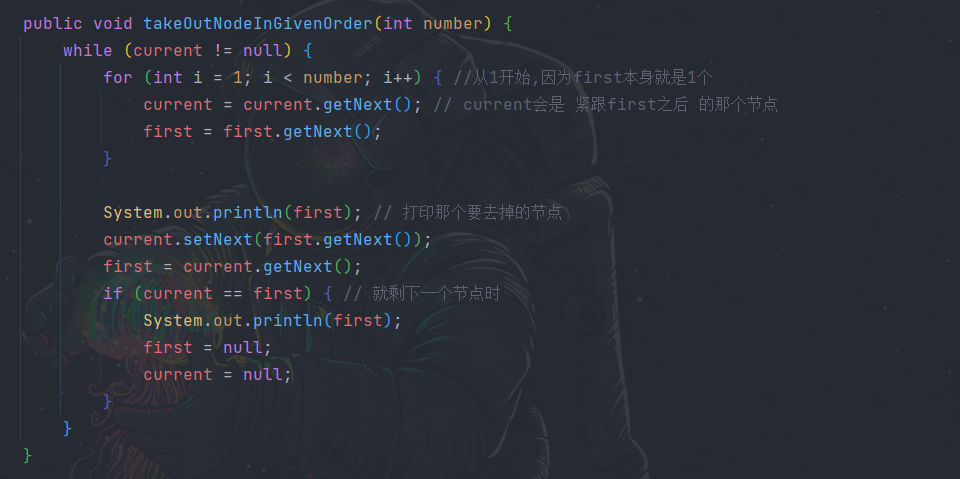
- 那么就需要从第一个开始打印出 2->4->1->5->3, 看下面具体讲解,大体就是数两个数 (第一个算一个数), 然后去掉那个数第二个数的 (因为用户给的数字就是 2), 然后再从第二个数被去掉的节点的下一个开始数,so on… 直到只剩一个节点,一个节点上面说过他的 next 指向的还是他自己,所以最后也就是他自己数两个数,然后自己去掉了,最后环形链表空出来
我的方式:
# 5.1、单向环形链表应用场景
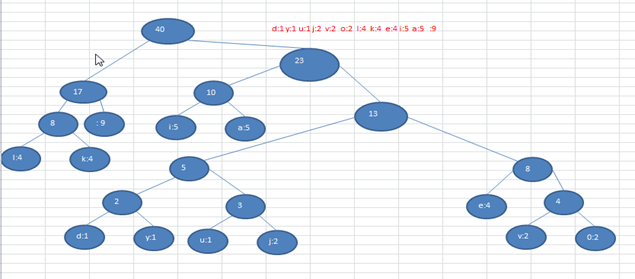
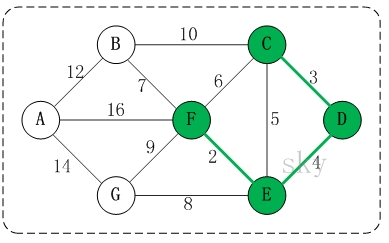
- Josephu 问题为: 设编号为 1, 2, … n 的 n 个人围坐一圈, 约定编号为 k(1<=k<=n) 的人从 1 开始报数, 数到 m 的那个人出列, 它的下一位又从 1 开始报数, 数到 m 的那个人又出列, 依次类推, 直到所有人出列为止, 由此产生一个出队编号的序列。
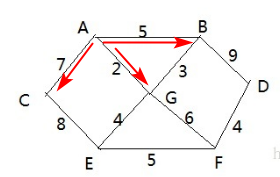
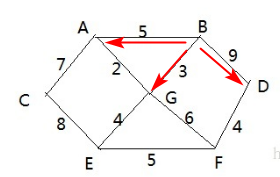
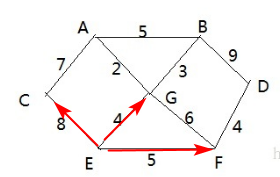
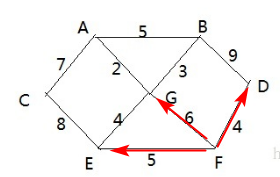
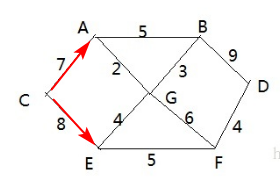
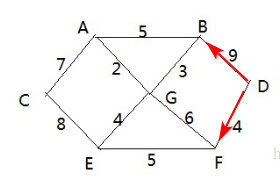
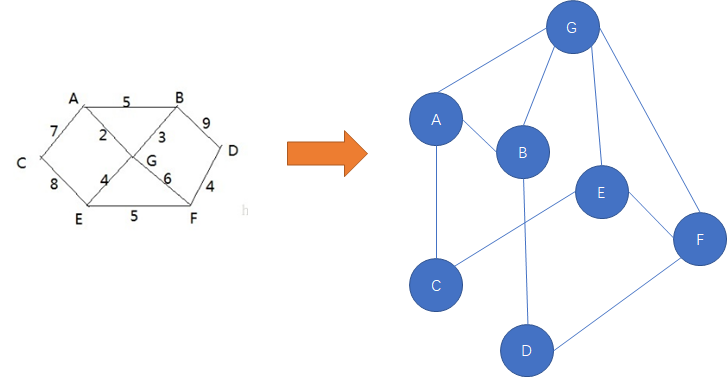
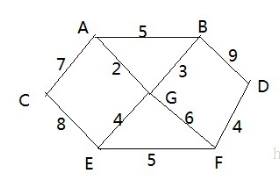
# 5.2、单向环形链表图解
# 5.3、Josephu 问题
- 用一个不带头结点的循环链表来处理 Josephu 问题: 先构成一个有 n 个结点的单循环链表, 然后由 k 结点起从 1 开始计数, 计到 m 时, 对应结点从链表中删除, 然后再从被删除结点的下一个结点又从 1 开始计数, 直到最后一个结点从链表中删除算法结束。
# 5.4、环形链表的构建与遍历
# 5.4.1、Boy 节点的定义
- Boy 节点就是个普普通通的单向链表节点
// 创建一个Boy类,表示一个节点
class Boy {
private int no;// 编号
private Boy next; // 指向下一个节点,默认null
public Boy(int no) {
this.no = no;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public Boy getNext() {
return next;
}
public void setNext(Boy next) {
this.next = next;
}
}# 5.4.2、单向循环链表的定义
- first 节点为单向循环链表的首节点,是真实存放数据的节点,不是头结点
// 创建一个环形的单向链表
class CircleSingleLinkedList {
// 创建一个first节点,当前没有编号
private Boy first = null;
// ...
# 5.4.3、构建单向循环链表
# 1、代码思路
- 长度为 1 的情况:
- 新创建的 boy 节点即是首节点:first = boy;
- 自封闭(自己构成环形链表):first.setNext(first);
- 此时 first 节点既是首节点,也是尾节点,辅助指针也指向 first :curBoy = first;
- 长度不为 1 的情况:
- 将 boy 节点添加至环形链表的最后:curBoy.setNext(boy); ,curBoy 节点永远是环形链表的尾节点
- 构成环形链表(最):boy.setNext(first);
- 辅助指针后移,指向环形链表的尾节点:curBoy = boy;
# 2、代码实现
// 添加小孩节点,构建成一个环形的链表
public void addBoy(int nums) {
// nums 做一个数据校验
if (nums < 1) {
System.out.println("nums的值不正确");
return;
}
Boy curBoy = null; // 辅助指针,帮助构建环形链表
// 使用for来创建我们的环形链表
for (int i = 1; i <= nums; i++) {
// 根据编号,创建小孩节点
Boy boy = new Boy(i);
// 如果是第一个小孩
if (i == 1) {
first = boy; // 初始化 first 节点
first.setNext(first); // 构成环
curBoy = first; // 让curBoy指向第一个小孩
} else {
curBoy.setNext(boy); // 将 boy 节点加到链表尾部
boy.setNext(first); // 构成环
curBoy = boy; // curBoy 指针后移
}
}
}
# 5.4.4、遍历单向循环链表
# 1、代码思路
-
定义辅助变量 curBoy ,相当于一个指针,指向当前节点
-
何时退出 while 循环?当 curBoy 已经指向环形链表的尾节点:curBoy.getNext() == first
# 2、代码实现
// 遍历当前的环形链表
public void showBoy() {
// 判断链表是否为空
if (first == null) {
System.out.println("没有任何小孩~~");
return;
}
// 因为first不能动,因此我们仍然使用一个辅助指针完成遍历
Boy curBoy = first;
while (true) {
System.out.printf("小孩的编号 %d \n", curBoy.getNo());
if (curBoy.getNext() == first) {// 说明已经遍历完毕
break;
}
curBoy = curBoy.getNext(); // curBoy后移
}
}
# 5.5、解决 Josephu 问题
# 5.5.1、代码思路
- 辅助变量 helper :helper 永都指向环形链表的尾节点,环形链表的尾节点永远都指向首节点,可得出:helper.getNext() == first
- 如何将 helper 定位至环形链表的尾节点?
- 初始化时,让 helper = first ,此时 helper 指向环形链表的首节点
- while 循环终止条件?helper.getNext() == first :此时 helper 已经移动至环形链表的尾节点
- 如何定位至第 startNo 个节点?如果想要定位至第 2 个节点,那么则需要让 first 和 helper 都移动 1 步,所以让 first 和 helper 都移动 (startNo - 1) 步即可
- 如何数 nums 下?让 first 和 helper 都移动 (nums - 1) 步即可
- 如何实现出圈?
- 我们需要将 first 指向的节点出圈,first 前一个节点的地址在 helper 中存着(环形链表)
- 先让 first 后移一步:first = first.getNext;
- 出圈:helper.setNext(first); ,原来的 first 节点由于没有任何引用,便会被垃圾回收机制回收
- while 循环终止条件?圈中只剩一人:helper == first
# 5.5.2、代码实现
// 根据用户的输入,计算出小孩出圈的顺序
/**
*
* @param startNo 表示从第几个小孩开始数数
* @param countNum 表示数几下
* @param nums 表示最初有多少小孩在圈中
*/
public void countBoy(int startNo, int countNum, int nums) {
// 先对数据进行校验
if (first == null || startNo < 1 || startNo > nums) {
System.out.println("参数输入有误, 请重新输入");
return;
}
// 创建要给辅助指针,帮助完成小孩出圈
Boy helper = first;
// 需求创建一个辅助指针(变量) helper , 事先应该指向环形链表的最后这个节点
while (true) {
if (helper.getNext() == first) { // 说明helper指向最后小孩节点
break;
}
helper = helper.getNext();
}
// 小孩报数前,先让 first 和 helper 移动 k - 1次
for (int j = 0; j < startNo - 1; j++) {
first = first.getNext();
helper = helper.getNext();
}
// 当小孩报数时,让first 和 helper 指针同时 的移动 m - 1 次, 然后出圈
// 这里是一个循环操作,知道圈中只有一个节点
while (true) {
if (helper == first) { // 说明圈中只有一个节点
break;
}
// 让 first 和 helper 指针同时 的移动 countNum - 1
for (int j = 0; j < countNum - 1; j++) {
first = first.getNext();
helper = helper.getNext();
}
// 这时first指向的节点,就是要出圈的小孩节点
System.out.printf("小孩%d出圈\n", first.getNo());
// 这时将first指向的小孩节点出圈
first = first.getNext();
helper.setNext(first);
}
System.out.printf("最后留在圈中的小孩编号%d \n", first.getNo());
}# 5.6、Josephu 问题测试
# 5.6.1、测试代码
public static void main(String[] args) {
// 测试一把看看构建环形链表,和遍历是否ok
CircleSingleLinkedList circleSingleLinkedList = new CircleSingleLinkedList();
circleSingleLinkedList.addBoy(5);// 加入5个小孩节点
circleSingleLinkedList.showBoy();
// 测试一把小孩出圈是否正确
circleSingleLinkedList.countBoy(1, 2, 3); // 2->4->1->5->3
}
# 5.6.2、程序运行结果
小孩的编号 1
小孩的编号 2
小孩的编号 3
小孩的编号 4
小孩的编号 5
小孩2出圈
小孩4出圈
小孩1出圈
小孩5出圈
最后留在圈中的小孩编号3
# 5.7、Josephu 问题所有代码
public class Josepfu {
public static void main(String[] args) {
// 测试一把看看构建环形链表,和遍历是否ok
CircleSingleLinkedList circleSingleLinkedList = new CircleSingleLinkedList();
circleSingleLinkedList.addBoy(5);// 加入5个小孩节点
circleSingleLinkedList.showBoy();
// 测试一把小孩出圈是否正确
circleSingleLinkedList.countBoy(1, 2, 3); // 2->4->1->5->3
}
}
// 创建一个环形的单向链表
class CircleSingleLinkedList {
// 创建一个first节点,当前没有编号
private Boy first = null;
// 添加小孩节点,构建成一个环形的链表
public void addBoy(int nums) {
// nums 做一个数据校验
if (nums < 1) {
System.out.println("nums的值不正确");
return;
}
Boy curBoy = null; // 辅助指针,帮助构建环形链表
// 使用for来创建我们的环形链表
for (int i = 1; i <= nums; i++) {
// 根据编号,创建小孩节点
Boy boy = new Boy(i);
// 如果是第一个小孩
if (i == 1) {
first = boy; // 初始化 first 节点
first.setNext(first); // 构成环
curBoy = first; // 让curBoy指向第一个小孩
} else {
curBoy.setNext(boy); // 将 boy 节点加到链表尾部
boy.setNext(first); // 构成环
curBoy = boy; // curBoy 指针后移
}
}
}
// 遍历当前的环形链表
public void showBoy() {
// 判断链表是否为空
if (first == null) {
System.out.println("没有任何小孩~~");
return;
}
// 因为first不能动,因此我们仍然使用一个辅助指针完成遍历
Boy curBoy = first;
while (true) {
System.out.printf("小孩的编号 %d \n", curBoy.getNo());
if (curBoy.getNext() == first) {// 说明已经遍历完毕
break;
}
curBoy = curBoy.getNext(); // curBoy后移
}
}
// 根据用户的输入,计算出小孩出圈的顺序
/**
*
* @param startNo 表示从第几个小孩开始数数
* @param countNum 表示数几下
* @param nums 表示最初有多少小孩在圈中
*/
public void countBoy(int startNo, int countNum, int nums) {
// 先对数据进行校验
if (first == null || startNo < 1 || startNo > nums) {
System.out.println("参数输入有误, 请重新输入");
return;
}
// 创建要给辅助指针,帮助完成小孩出圈
Boy helper = first;
// 需求创建一个辅助指针(变量) helper , 事先应该指向环形链表的最后这个节点
while (true) {
if (helper.getNext() == first) { // 说明helper指向最后小孩节点
break;
}
helper = helper.getNext();
}
// 小孩报数前,先让 first 和 helper 移动 k - 1次
for (int j = 0; j < startNo - 1; j++) {
first = first.getNext();
helper = helper.getNext();
}
// 当小孩报数时,让first 和 helper 指针同时 的移动 m - 1 次, 然后出圈
// 这里是一个循环操作,知道圈中只有一个节点
while (true) {
if (helper == first) { // 说明圈中只有一个节点
break;
}
// 让 first 和 helper 指针同时 的移动 countNum - 1
for (int j = 0; j < countNum - 1; j++) {
first = first.getNext();
helper = helper.getNext();
}
// 这时first指向的节点,就是要出圈的小孩节点
System.out.printf("小孩%d出圈\n", first.getNo());
// 这时将first指向的小孩节点出圈
first = first.getNext();
helper.setNext(first);
}
System.out.printf("最后留在圈中的小孩编号%d \n", first.getNo());
}
}
// 创建一个Boy类,表示一个节点
class Boy {
private int no;// 编号
private Boy next; // 指向下一个节点,默认null
public Boy(int no) {
this.no = no;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public Boy getNext() {
return next;
}
public void setNext(Boy next) {
this.next = next;
}
}# 5.8、总结
- 操作单向链表:对于插入、删除操作,只能定位至待操作节点的前一个节点,如果定位至当前节点,那么其上一个节点的信息便会丢失
# 栈 [STACK]
# 1、栈的基本介绍
- LIFO, 先进后出
- 其实数据底层可以用数组存 (模拟), 其实也可以拿链表实现的
- 有一个属性为 maxSize, 代表这个栈的最多存多少数据 (最大空间)
- 有一个属性,我们叫它为 top, 一开始是 - 1
- 当添加一个数据 (push), 我们 top++ 然后放到下标为 top 的位置
- 取出一个数据 (pop), 我们取出在 top 下标的那个数据,然后 top–
用栈完成计算一个数学表达式的结果,达到计算器的功能 (很简陋的一个,很多都没考虑到)
创建两个栈,一个用来存数字,一个用来存运算符
遍历那个表达式,把每个数字按顺序存入数字栈中,把每个运算符按顺序存入运算符栈中
对于扫描到的每个运算符
如果运算符栈当前为空,那么直接入栈
如果运算符栈已经有运算符,那么就会进行比较,如果当前的运算符比栈中的运算符的优先级
- 更小或等于,就从数字栈直接 pop 两个数字,从运算符栈 pop 出一个运算符,进行运算,然后把结果放到入数栈, 然后把当前的运算符直接放入运算符栈 (也就是说如果现在运算符栈是已经有乘或者除,现在放入一个减 / 加 / 乘 / 除都会让之前的运算符 pop 出来然后数栈 pop 出来两个这个运算符对应的数字进行计算,所以那个运算符栈中那个优先级更大或者同等级直接先算好了,之后你直接放入当前的运算符到栈里面就随便。没影响)
- 更大,那么当前运算符直接入栈,不 pop 然后计算什么 (指的是是运算符中有的是加 / 减,然后放入乘 / 除,这样随便,反正到时候结束了扫描需要从上面开始 pop 然后因为乘 / 数我们是后加的,所以直接先被 pop 出来而且对应的数字也会被 pop 出来,所以还是会计算这个优先级更高的)
当前运算符和已经在运算符中的运算符进行比较优先级,可以通过 peek 方法 (而不是 pop) 获取到运算符中栈的那个运算符
当扫描结束时,就按照顺序从两个栈中 pop 出相应的数和符号,并计算
最后只会在数栈有一个数字,就是我们的表达式的结果
这个算法很垃圾,只能一位数的运算,而且什么 () 都不能用等等等
前缀,中缀和后缀表达式
后缀表达式使用的最多,更容易理解
后缀表达式 (逆波兰表达式) 计算器
接收按照后缀表达式方式的字符串 (就数字和运算符的顺序已经按照后缀表达式的 way 来 organise 好了)
- 遍历那个字符串 (或者按照分隔符把数组放到一个 list 集合等等等就可以计算多位数的,不过需要分隔符比如说空格)
- 如果当前的是个数字那就把数字放入 stack 中 (后缀表达式的方式,我们就用一个 stack 足以)
- 如果当前的是个运算符那就直接从栈中 pop 出两个数字,然后按照当前运算符进行计算,注意顺序 (比如说是后 pop 出来的 - 先 pop 出来的)!!
- 把结果重新放回栈中
- 结束放回栈中
- 遍历结束,就从栈中 pop 一下就是最终结果
(细节看下面的)
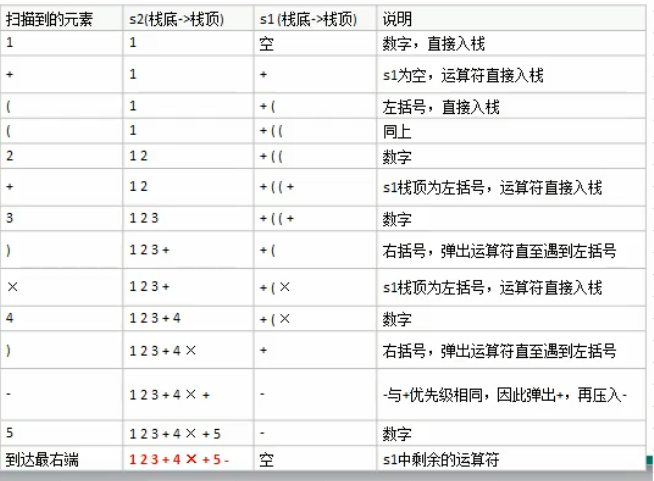
中缀表达式我们很好理解,后缀表达式计算机很好理解,所以如何把中缀表达式转换成后缀表达式?
其实还是很好理解的
就是如果遇到优先级更高的运算符放在栈的上面,这样之后 s1 弹出的时候就把那个运算符放入 s2, 然后每一个 (…) 和里面的运算符会被当做一个整体 (看视频更好理解)
https://www.bilibili.com/video/BV1E4411H73v?p=39
其实 s2 可以是个队列,这样存进然后之后取出来就不需要特意逆序一下获取到真正的后缀表达式
# 1.1、栈的实际需求
- 请计算表达式:[7_2_2-5+1-5+3-3] 的值
- 请问:计算机底层是如何运算得到结果的? 注意不是简单的把算式列出运算,因为我们看这个算式 7 * 2 * 2 - 5,但是计算机怎么理解这个算式的
- 对计算机而言, 它接收到的就是一个字符串, 我们讨论的是这个问题:栈
# 1.2、栈的基本性质
- 栈的英文为 (stack)
- 栈是一个先入后出 (FILO-First In Last Out) 的有序列表
- 栈 (stack) 是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。 允许插入和删除的一端, 为变化的一端, 称为栈顶 (Top), 另一端为固定的一端, 称为栈底 (Bottom)。
- 根据栈的定义可知, 最先放入栈中元素在栈底, 最后放入的元素在栈顶, 而删除元素刚好相反, 最后放入的元素最先删除, 最先放入的元素最后删除
- 图解方式说明出栈 (pop) 和入栈 (push) 的概念
# 1.3、栈的应用场景
- 子程序的调用: 在跳往子程序前, 会先将下个指令的地址存到堆栈中, 直到子程序执行完后再将地址取出, 以回到原来的程序中。
- 处理递归调用: 和子程序的调用类似, 只是除了储存下一个指令的地址外, 也将参数、 区域变量等数据存入栈中。
- 表达式的转换: [中缀表达式转后缀表达式] 与求值 (实际解决)。
- 二叉树的遍历。
- 图形的深度优先 (depth 一 first) 搜索法。
# 2、数组模拟栈
# 2.1、代码思路
- maxSize :栈的大小(数组的大小)
- arr :用来模拟栈的数组
- top :指向当前栈顶元素,初始值为 -1 ,表示栈空
- 判断栈满:top == maxSize ,即已经到达数组最后一个位置
- 判断栈空:top == -1
- 入栈:arr[++top] = arr;
- 出栈:return arr[top–] ;
# 2.2、代码实现
- 栈的定义
//定义一个 ArrayStack 表示栈
class ArrayStack {
private int maxSize; // 栈的大小
private int[] stack; // 数组,数组模拟栈,数据就放在该数组
private int top = -1;// top表示栈顶,初始化为-1
// 构造器
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
// 栈满
public boolean isFull() {
return top == maxSize - 1;
}
// 栈空
public boolean isEmpty() {
return top == -1;
}
// 入栈-push
public void push(int value) {
// 先判断栈是否满
if (isFull()) {
System.out.println("栈满");
return;
}
top++;
stack[top] = value;
}
// 出栈-pop, 将栈顶的数据返回
public int pop() {
// 先判断栈是否空
if (isEmpty()) {
// 抛出异常
throw new RuntimeException("栈空,没有数据~");
}
int value = stack[top];
top--;
return value;
}
// 显示栈的情况[遍历栈], 遍历时,需要从栈顶开始显示数据
public void list() {
if (isEmpty()) {
System.out.println("栈空,没有数据~~");
return;
}
// 需要从栈顶开始显示数据
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
}- 测试代码
public static void main(String[] args) {
// 测试一下ArrayStack 是否正确
// 先创建一个ArrayStack对象->表示栈
ArrayStack stack = new ArrayStack(4);
String key = "";
boolean loop = true; // 控制是否退出菜单
Scanner scanner = new Scanner(System.in);
while (loop) {
System.out.println("show: 表示显示栈");
System.out.println("exit: 退出程序");
System.out.println("push: 表示添加数据到栈(入栈)");
System.out.println("pop: 表示从栈取出数据(出栈)");
System.out.println();
System.out.println("请输入你的选择");
key = scanner.next();
switch (key) {
case "show":
stack.list();
break;
case "push":
System.out.println("请输入一个数");
int value = scanner.nextInt();
stack.push(value);
break;
case "pop":
try {
int res = stack.pop();
System.out.printf("出栈的数据是 %d\n", res);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
break;
case "exit":
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("程序退出~~~");
}- 程序运行结果
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
push
请输入一个数
1
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
push
请输入一个数
2
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
push
请输入一个数
3
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
push
请输入一个数
4
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
push
请输入一个数
5
栈满
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
show
stack[3]=4
stack[2]=3
stack[1]=2
stack[0]=1
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
pop
出栈的数据是 4
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
pop
出栈的数据是 3
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
pop
出栈的数据是 2
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
pop
出栈的数据是 1
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择
pop
栈空,没有数据~
show: 表示显示栈
exit: 退出程序
push: 表示添加数据到栈(入栈)
pop: 表示从栈取出数据(出栈)
请输入你的选择# 2.3、数组模拟栈全部代码
`public class ArrayStackDemo {
public static void main(String[] args) {
// 测试一下ArrayStack 是否正确
// 先创建一个ArrayStack对象->表示栈
ArrayStack stack = new ArrayStack(4);
String key = "";
boolean loop = true; // 控制是否退出菜单
Scanner scanner = new Scanner(System.in);
while (loop) {
System.out.println("show: 表示显示栈");
System.out.println("exit: 退出程序");
System.out.println("push: 表示添加数据到栈(入栈)");
System.out.println("pop: 表示从栈取出数据(出栈)");
System.out.println();
System.out.println("请输入你的选择");
key = scanner.next();
switch (key) {
case "show":
stack.list();
break;
case "push":
System.out.println("请输入一个数");
int value = scanner.nextInt();
stack.push(value);
break;
case "pop":
try {
int res = stack.pop();
System.out.printf("出栈的数据是 %d\n", res);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
break;
case "exit":
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("程序退出~~~");
}
}
//定义一个 ArrayStack 表示栈
class ArrayStack {
private int maxSize; // 栈的大小
private int[] stack; // 数组,数组模拟栈,数据就放在该数组
private int top = -1;// top表示栈顶,初始化为-1
// 构造器
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
// 栈满
public boolean isFull() {
return top == maxSize - 1;
}
// 栈空
public boolean isEmpty() {
return top == -1;
}
// 入栈-push
public void push(int value) {
// 先判断栈是否满
if (isFull()) {
System.out.println("栈满");
return;
}
top++;
stack[top] = value;
}
// 出栈-pop, 将栈顶的数据返回
public int pop() {
// 先判断栈是否空
if (isEmpty()) {
// 抛出异常
throw new RuntimeException("栈空,没有数据~");
}
int value = stack[top];
top--;
return value;
}
// 显示栈的情况[遍历栈], 遍历时,需要从栈顶开始显示数据
public void list() {
if (isEmpty()) {
System.out.println("栈空,没有数据~~");
return;
}
// 需要从栈顶开始显示数据
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
}# 2.4、课后练习
- 使用链表模拟栈
# 3、栈实现综合计算器 (中缀表达式)
# 3.1、代码思路
-
栈分为两个栈:
- 数栈(numStack):存储表达式中的数字
- 符号栈(operStack):存储表达式中的符号
-
扫描表达式(这里并没有考虑括号):
- 对于数:扫描到数,则直接压入数栈
- 对于运算符:扫描到运算符,分为如下几种情况:
- 如果符号栈为空,则直接入栈
- 如果符号栈不为空:
- 如果当前扫描到的运算符的优先级 <= 符号栈栈顶的运算符的优先级,说明上次的运算符优先级较高,先执行优先级高的运算
- 从数栈中弹出两个数,根据符号栈栈顶的运算符进行运算(优先级高,就先算出来)
- 然后将计算的结果压入栈中
- 再将当前运算符压入符号栈
- 如果当前扫描到的运算符的优先级 > 符号栈栈顶的运算符的优先级,说明上次的运算符优先级较低,直接压入符号栈
- 如果当前扫描到的运算符的优先级 <= 符号栈栈顶的运算符的优先级,说明上次的运算符优先级较高,先执行优先级高的运算
-
何时停止循环?
- 处理完表达式,退出循环
- 即表达式下标(index)的值大于表达式(expression)的长度
- 代码:index >= expression.length()
-
表达式扫描完成:
- 此时符号栈中的运算符优先级都相同
- 从数栈中弹出两个数,再从符号栈中弹出一个运算符,进行运算,计算结果放回数栈中
- 何时停止循环?符号栈为空则停止:operStack.isEmpty()
- 表达式的值?符号栈为空时,数栈栈顶还有一个元素,这个元素的值就是表达式的值
-
举例:3+2*6-2
- 首先
- 将 3 压入数栈
- 将 + 压入符号栈
- 将 2 压入数栈
2 3 + 数栈 符号栈- 由于 * 优先级大于 + ,所以将 * 压入 符号栈,然后将 6 压入数栈
6 2 * 3 + 数栈 符号栈- 由于 - 优先级低于 * ,所以从数栈中弹出两个数(6 和 2),从符号栈中弹出一个运算符(*),进行运算,运算结果再压入数栈,然后将 - 压入符号栈
12 - 3 + 数栈 符号栈- 将 2 压入数栈,表达式处理完毕
2 12 - 3 + 数栈 符号栈- 重复此过程,直至符号栈为空:从数栈中弹出两个数,再从符号栈中弹出一个运算符,进行运算,计算结果放回数栈中
10 3 + 数栈 符号栈13 数栈 符号栈 - 首先
# 3.2、代码实现
- 栈的定义:专为计算器而生的栈
- 对于乘除法特别说明:由于栈先进后出的特点,num1 是运算符后面的数(减数、除数),num2 是运算符前的数(被减数、被除数),特别需要注意减法与除法的顺序
- res = num2 - num1;
- res = num2 / num1;
//先创建一个栈,直接使用前面创建好
//定义一个 CalcStack 表示栈, 需要扩展功能
class CalcStack {
private int maxSize; // 栈的大小
private int[] stack; // 数组,数组模拟栈,数据就放在该数组
private int top = -1;// top表示栈顶,初始化为-1
// 构造器
public CalcStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
// 增加一个方法,可以返回当前栈顶的值, 但是不是真正的pop
public int peek() {
return stack[top];
}
// 栈满
public boolean isFull() {
return top == maxSize - 1;
}
// 栈空
public boolean isEmpty() {
return top == -1;
}
// 入栈-push
public void push(int value) {
// 先判断栈是否满
if (isFull()) {
System.out.println("栈满");
return;
}
top++;
stack[top] = value;
}
// 出栈-pop, 将栈顶的数据返回
public int pop() {
// 先判断栈是否空
if (isEmpty()) {
// 抛出异常
throw new RuntimeException("栈空,没有数据~");
}
int value = stack[top];
top--;
return value;
}
// 显示栈的情况[遍历栈], 遍历时,需要从栈顶开始显示数据
public void list() {
if (isEmpty()) {
System.out.println("栈空,没有数据~~");
return;
}
// 需要从栈顶开始显示数据
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
// 返回运算符的优先级,优先级是程序员来确定, 优先级使用数字表示
// 数字越大,则优先级就越高.
public int priority(int oper) {
if (oper == '*' || oper == '/') {
return 1;
} else if (oper == '+' || oper == '-') {
return 0;
} else {
return -1; // 假定目前的表达式只有 +, - , * , /
}
}
// 判断是不是一个运算符
public boolean isOper(char val) {
return val == '+' || val == '-' || val == '*' || val == '/';
}
// 计算方法
public int cal(int num1, int num2, int oper) {
int res = 0; // res 用于存放计算的结果
switch (oper) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;// 注意顺序
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num2 / num1;
break;
default:
break;
}
return res;
}
}- 综合计算器代码:对多位数进行了判断,使得程序可处理多位数的运算
public static void main(String[] args) {
// 根据前面老师思路,完成表达式的运算
String expression = "7*2*2-5+1-5+3-4"; // 如何处理多位数的问题?
// 创建两个栈,一个数栈,一个符号栈
CalcStack numStack = new CalcStack(10);
CalcStack operStack = new CalcStack(10);
// 定义需要的相关变量
int index = 0;// 用于扫描
int num1 = 0;
int num2 = 0;
int oper = 0;
int res = 0;
char ch = ' '; // 将每次扫描得到char保存到ch
String keepNum = ""; // 用于拼接 多位数
// 开始while循环的扫描expression
while (true) {
// 依次得到expression 的每一个字符
ch = expression.substring(index, index + 1).charAt(0);
// 判断ch是什么,然后做相应的处理
if (operStack.isOper(ch)) {// 如果是运算符
// 判断当前的符号栈是否为空
if (!operStack.isEmpty()) {
// 如果符号栈有操作符,就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符,就需要从数栈中pop出两个数,
// 在从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符入符号栈
if (operStack.priority(ch) <= operStack.priority(operStack.peek())) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
// 把运算的结果如数栈
numStack.push(res);
// 然后将当前的操作符入符号栈
operStack.push(ch);
} else {
// 如果当前的操作符的优先级大于栈中的操作符, 就直接入符号栈.
operStack.push(ch);
}
} else {
// 如果为空直接入符号栈..
operStack.push(ch); // 1 + 3
}
} else { // 如果是数,则直接入数栈
// numStack.push(ch - 48); //? "1+3" '1' => 1
// 分析思路
// 1. 当处理多位数时,不能发现是一个数就立即入栈,因为他可能是多位数
// 2. 在处理数,需要向expression的表达式的index 后再看一位,如果是数就进行扫描,如果是符号才入栈
// 3. 因此我们需要定义一个变量 字符串,用于拼接
// 处理多位数
keepNum += ch;
// 如果ch已经是expression的最后一位,就直接入栈
if (index == expression.length() - 1) {
numStack.push(Integer.parseInt(keepNum));
} else {
// 判断下一个字符是不是数字,如果是数字,就继续扫描,如果是运算符,则入栈
// 注意是看后一位,不是index++
if (operStack.isOper(expression.substring(index + 1, index + 2).charAt(0))) {
// 如果后一位是运算符,则入栈 keepNum = "1" 或者 "123"
numStack.push(Integer.parseInt(keepNum));
// 重要的!!!!!!, keepNum清空
keepNum = "";
}
}
}
// 让index + 1, 并判断是否扫描到expression最后.
index++;
if (index >= expression.length()) {
break;
}
}
// 当表达式扫描完毕,就顺序的从 数栈和符号栈中pop出相应的数和符号,并运行.
while (true) {
// 如果符号栈为空,则计算到最后的结果, 数栈中只有一个数字【结果】
if (operStack.isEmpty()) {
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
numStack.push(res);// 入栈
}
// 将数栈的最后数,pop出,就是结果
res = numStack.pop();
System.out.printf("表达式 %s = %d", expression, res);
}- 程序运行结果
表达式 7*2*2-5+1-5+3-4 = 18# 3.3、综合计算器全部代码
public class Calculator {
public static void main(String[] args) {
// 根据前面老师思路,完成表达式的运算
String expression = "7*2*2-5+1-5+3-4"; // 如何处理多位数的问题?
// 创建两个栈,一个数栈,一个符号栈
CalcStack numStack = new CalcStack(10);
CalcStack operStack = new CalcStack(10);
// 定义需要的相关变量
int index = 0;// 用于扫描
int num1 = 0;
int num2 = 0;
int oper = 0;
int res = 0;
char ch = ' '; // 将每次扫描得到char保存到ch
String keepNum = ""; // 用于拼接 多位数
// 开始while循环的扫描expression
while (true) {
// 依次得到expression 的每一个字符
ch = expression.substring(index, index + 1).charAt(0);
// 判断ch是什么,然后做相应的处理
if (operStack.isOper(ch)) {// 如果是运算符
// 判断当前的符号栈是否为空
if (!operStack.isEmpty()) {
// 如果符号栈有操作符,就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符,就需要从数栈中pop出两个数,
// 在从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符入符号栈
if (operStack.priority(ch) <= operStack.priority(operStack.peek())) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
// 把运算的结果如数栈
numStack.push(res);
// 然后将当前的操作符入符号栈
operStack.push(ch);
} else {
// 如果当前的操作符的优先级大于栈中的操作符, 就直接入符号栈.
operStack.push(ch);
}
} else {
// 如果为空直接入符号栈..
operStack.push(ch); // 1 + 3
}
} else { // 如果是数,则直接入数栈
// numStack.push(ch - 48); //? "1+3" '1' => 1
// 分析思路
// 1. 当处理多位数时,不能发现是一个数就立即入栈,因为他可能是多位数
// 2. 在处理数,需要向expression的表达式的index 后再看一位,如果是数就进行扫描,如果是符号才入栈
// 3. 因此我们需要定义一个变量 字符串,用于拼接
// 处理多位数
keepNum += ch;
// 如果ch已经是expression的最后一位,就直接入栈
if (index == expression.length() - 1) {
numStack.push(Integer.parseInt(keepNum));
} else {
// 判断下一个字符是不是数字,如果是数字,就继续扫描,如果是运算符,则入栈
// 注意是看后一位,不是index++
if (operStack.isOper(expression.substring(index + 1, index + 2).charAt(0))) {
// 如果后一位是运算符,则入栈 keepNum = "1" 或者 "123"
numStack.push(Integer.parseInt(keepNum));
// 重要的!!!!!!, keepNum清空
keepNum = "";
}
}
}
// 让index + 1, 并判断是否扫描到expression最后.
index++;
if (index >= expression.length()) {
break;
}
}
// 当表达式扫描完毕,就顺序的从 数栈和符号栈中pop出相应的数和符号,并运行.
while (true) {
// 如果符号栈为空,则计算到最后的结果, 数栈中只有一个数字【结果】
if (operStack.isEmpty()) {
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.cal(num1, num2, oper);
numStack.push(res);// 入栈
}
// 将数栈的最后数,pop出,就是结果
res = numStack.pop();
System.out.printf("表达式 %s = %d", expression, res);
}
}
//先创建一个栈,直接使用前面创建好
//定义一个 CalcStack 表示栈, 需要扩展功能
class CalcStack {
private int maxSize; // 栈的大小
private int[] stack; // 数组,数组模拟栈,数据就放在该数组
private int top = -1;// top表示栈顶,初始化为-1
// 构造器
public CalcStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
// 增加一个方法,可以返回当前栈顶的值, 但是不是真正的pop
public int peek() {
return stack[top];
}
// 栈满
public boolean isFull() {
return top == maxSize - 1;
}
// 栈空
public boolean isEmpty() {
return top == -1;
}
// 入栈-push
public void push(int value) {
// 先判断栈是否满
if (isFull()) {
System.out.println("栈满");
return;
}
top++;
stack[top] = value;
}
// 出栈-pop, 将栈顶的数据返回
public int pop() {
// 先判断栈是否空
if (isEmpty()) {
// 抛出异常
throw new RuntimeException("栈空,没有数据~");
}
int value = stack[top];
top--;
return value;
}
// 显示栈的情况[遍历栈], 遍历时,需要从栈顶开始显示数据
public void list() {
if (isEmpty()) {
System.out.println("栈空,没有数据~~");
return;
}
// 需要从栈顶开始显示数据
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
// 返回运算符的优先级,优先级是程序员来确定, 优先级使用数字表示
// 数字越大,则优先级就越高.
public int priority(int oper) {
if (oper == '*' || oper == '/') {
return 1;
} else if (oper == '+' || oper == '-') {
return 0;
} else {
return -1; // 假定目前的表达式只有 +, - , * , /
}
}
// 判断是不是一个运算符
public boolean isOper(char val) {
return val == '+' || val == '-' || val == '*' || val == '/';
}
// 计算方法
public int cal(int num1, int num2, int oper) {
int res = 0; // res 用于存放计算的结果
switch (oper) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;// 注意顺序
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num2 / num1;
break;
default:
break;
}
return res;
}
}# 3.4、课后练习
- 加入小括号的判断:小括号内的运算需要优先执行,也即小括号的优先级最高
- 我的代码思路如下:
- 但凡遇到左括号,直接入符号栈,之后的操作和之前的一样
- 直至遇到右括号,此时可以依次将符号栈中的符号弹出,与数栈中的数做运算
- 直至符号栈弹出左括号为止,此时,括号内的运算已执行完毕
# 4、前缀 中缀 后缀表达式
# 4.1、前缀表达式 (波兰表达式)
# 4.1.1、前缀表达式
- 前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前
- 举例说明: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6
# 4.1.2、前缀表达式的计算机求值
-
从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果
-
例如:(3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:
- 从右至左扫描,将 6、5、4、3 压入堆栈
- 遇到 + 运算符,因此弹出 3 和 4(3 为栈顶元素,4 为次顶元素),计算出 3+4 的值,得 7,再将 7 入栈
- 接下来是 × 运算符,因此弹出 7 和 5,计算出 7×5=35,将 35 入栈
- 最后是 - 运算符,计算出 35-6 的值,即 29,由此得出最终结果
# 4.2、中缀表达式
- 中缀表达式就是常见的运算表达式,如 (3+4)×5-6
- 中缀表达式的求值是我们人最熟悉的,但是对计算机来说却不好操作 (前面我们讲的案例就能看的这个问题,因为中缀表达式存在运算符优先级的问题),因此,在计算结果时,往往会将中缀表达式转成其它表达式来操作 (一般转成后缀表达式)
# 4.3、后缀表达式
# 4.3.1、后缀表达式
- 后缀表达式又称逆波兰表达式,与前缀表达式相似,只是运算符位于操作数之后
- 中缀表达式举例说明: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –
- 再比如:
| 正常的表达式 | 逆波兰表达式 |
|---|---|
| a+b | a b + |
| a+(b-c) | a b c - + |
| a+(b-c)*d | a b c – d * + |
| a+d*(b-c) | a d b c - * + |
| a=1+3 | a 1 3 + = |
# 4.3.2、后缀表达式的计算机求值
-
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
-
例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:
- 从左至右扫描,将 3 和 4 压入堆栈;
- 遇到 + 运算符,因此弹出 4 和 3(4 为栈顶元素,3 为次顶元素),计算出 3+4 的值,得 7,再将 7 入栈;
- 将 5 入栈;
- 接下来是 × 运算符,因此弹出 5 和 7,计算出 7×5=35,将 35 入栈;
- 将 6 入栈;
- 最后是 - 运算符,计算出 35-6 的值,即 29,由此得出最终结果
# 5、逆波兰计算器
# 5.1、计算器说明
- 输入一个逆波兰表达式 (后缀表达式), 使用栈 (Stack),计算其结果
- 支持小括号和多位数整数, 因为这里我们主要讲的是数据结构, 因此计算器进行简化, 只支持对整数的计算
# 5.2、代码思路
- 计算后缀表达式无需考虑运算符优先级问题,所以只需要一个数栈即可
- 分为两种情况:
- 遇到数:压入数栈
- 遇到运算符:从数栈中弹出两个数,进行计算,计算结果压入数栈
- 何时计算完成?处理完表达式就代表计算完成
# 5.3、代码实现
- 出栈的两个数:num2 和 num1
- num2 先出栈,所以 num2 是减数或除数
- num1 后出栈,所以 num1 是被减数或被除数
public class PolandNotation {
public static void main(String[] args) {
//先定义给逆波兰表达式
// 4 * 5 - 8 + 60 + 8 / 2 => 4 5 * 8 - 60 + 8 2 / +
//说明为了方便,逆波兰表达式 的数字和符号使用空格隔开
String suffixExpression = "4 5 * 8 - 60 + 8 2 / +"; // 76
//思路
//1. 先将逆波兰表达式 => 放到ArrayList中
//2. 将 ArrayList 传递给一个方法,遍历 ArrayList 配合栈 完成计算
List<String> list = getListString(suffixExpression);
System.out.println("rpnList=" + list);
int res = calculate(list);
System.out.println("计算的结果是=" + res);
}
//将一个逆波兰表达式, 依次将数据和运算符 放入到 ArrayList中
public static List<String> getListString(String suffixExpression) {
//将 suffixExpression 分割
String[] split = suffixExpression.split(" ");
List<String> list = new ArrayList<String>();
for(String ele: split) {
list.add(ele);
}
return list;
}
//完成对逆波兰表达式的运算
/*
* 1)从左至右扫描,将3和4压入堆栈;
2)遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素),计算出3+4的值,得7,再将7入栈;
3)将5入栈;
4)接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;
5)将6入栈;
6)最后是-运算符,计算出35-6的值,即29,由此得出最终结果
*/
public static int calculate(List<String> ls) {
// 创建给栈, 只需要一个栈即可
Stack<String> stack = new Stack<String>();
// 遍历 ls
for (String item : ls) {
// 这里使用正则表达式来取出数
if (item.matches("\\d+")) { // 匹配的是多位数
// 入栈
stack.push(item);
} else {
// pop出两个数,并运算, 再入栈
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
if (item.equals("+")) {
res = num1 + num2;
} else if (item.equals("-")) {
res = num1 - num2;
} else if (item.equals("*")) {
res = num1 * num2;
} else if (item.equals("/")) {
res = num1 / num2;
} else {
throw new RuntimeException("运算符有误");
}
//把res 入栈
stack.push("" + res);
}
}
//最后留在stack中的数据是运算结果
return Integer.parseInt(stack.pop());
}
}- 程序运行结果
rpnList=[4, 5, *, 8, -, 60, +, 8, 2, /, +]
计算的结果是=76
# 6、中缀表达式转后缀表达式
# 6.1、代码思路
-
大家看到,后缀表达式适合计算式进行运算,但是人却不太容易写出来,尤其是表达式很长的情况下,因此在开发中,我们需要将中缀表达式转成后缀表达式。
-
具体步骤如下:
- 初始化两个栈:运算符栈 operStack 和储存中间结果的栈 tempStack;
- 从左至右扫描中缀表达式;
- 遇到操作数时,将其压 tempStack;
- 遇到运算符时,比较其与 operStack 栈顶运算符的优先级:
- 如果 operStack 为空,或栈顶运算符为左括号 “(”,则直接将此运算符入 tempStack 栈(分如下两种情况)
- operStack 栈顶为空:之前的优先级别高的运算已经处理完成,已经得到了一个结果,将当前运算符直接压入 operStack 栈即可
- operStack 栈顶为左括号:我都挨着左括号了,我要和它同生共死!当把我从 operStack 出栈,用于运算后,这对括号中的表达式的值也就计算出来了
- 如果当前运算符优先级比栈顶运算符的高,也将运算符压入 tempStack(当前运算符优先级高,先执行运算)
- 否则,当前运算符优先级 <= 栈顶运算符优先级,将 operStack 栈顶的运算符弹出并压入到 tempStack 中(operStack 栈顶运算符优先级高,先执行运算),再次转到 (4.1) 与 operStack 中新的栈顶运算符相比较(分如下两种情况);
- 一直循环,将 tempStack 栈顶元素取出,直到在 operStack 栈中找到比当前运算符优先级高的运算符,让其先执行运算
- 如果在 tempStack 栈中找不到比当前运算符优先级高的运算符,则会直接将 operStack 栈掏空,然后将当前运算符压入 tempStack 栈中(放在栈底)
- 如果 operStack 为空,或栈顶运算符为左括号 “(”,则直接将此运算符入 tempStack 栈(分如下两种情况)
- 遇到括号时:
- 如果是左括号 “(”,则直接压入 operStack,等待与其配对的右括号,因为括号中的表达式需要优先运算
- 如果是右括号 “)”,则依次弹出 operStack 栈顶的运算符,并压入 tempStack,直到遇到左括号为止,此时将这一对括号丢弃(此时括号内的运算完成,并将结果压入了 tempStack)
- 重复步骤 2 至 5,直到表达式的最右边
- 将 operStack 中剩余的运算符依次弹出并压入 tempStack(operStack 栈中剩下的运算都是优先级相同的运算符,按顺序执行即可)
- 依次弹出 tempStack 中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式
# 6.2、举例说明
- 举例说明:将中缀表达 式 “1+((2+3)×4)-5” 转换为后缀表达式的过程如下
- 因此结果为:“1 2 3 + 4 × + 5 –”
| 扫描到的元素 | tempStack (栈底 -> 栈顶) | operStack (栈底 -> 栈顶) | 说明 |
|---|---|---|---|
| 1 | 1 | 空 | 数字,直接入栈 |
| + | 1 | + | s1 为空,运算符直接入栈 |
| ( | 1 | + ( | 左括号,直接入栈 |
| ( | 1 | + ( ( | 同上 |
| 2 | 1 2 | + ( ( | 数字 |
| + | 1 2 | + ( ( + | s1 栈顶为左括号,运算符直接入栈 |
| 3 | 1 2 3 | + ( ( + | 数字 |
| ) | 1 2 3 + | + ( | 右括号,弹出运算符直至遇到左括号 |
| × | 1 2 3 + | + ( × | s1 栈顶为左括号,运算符直接入栈 |
| 4 | 1 2 3 + 4 | + ( × | 数字 |
| ) | 1 2 3 + 4 × | + | 右括号,弹出运算符直至遇到左括号 |
| - | 1 2 3 + 4 × + | - | - 与 + 优先级相同,因此弹出 +,再压入 - |
| 5 | 1 2 3 + 4 × + 5 | - | 数字 |
| 到达最右端 | 1 2 3 + 4 × + 5 - | 空 | s1 中剩余的运算符 |
# 6.3、代码实现
- 将中缀表达式转为对应的 List :将数字和运算符分开,存储在
List<String>对象中
// 方法:将 中缀表达式转成对应的List
// s="1+((2+3)×4)-5";
public static List<String> toInfixExpressionList(String s) {
// 定义一个List,存放中缀表达式 对应的内容
List<String> ls = new ArrayList<String>();
int i = 0; // 这时是一个指针,用于遍历 中缀表达式字符串
String str; // 对多位数的拼接
char c; // 每遍历到一个字符,就放入到c
do {
// 如果c是一个非数字,我需要加入到ls
if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
ls.add("" + c);
i++; // i需要后移
} else { // 如果是一个数,需要考虑多位数
str = ""; // 先将str 置成"" '0'[48]->'9'[57]
while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
str += c;// 拼接
i++;
}
ls.add(str);
}
} while (i < s.length());
return ls;// 返回
}- 将中缀表达式(List)转为后缀表达式(List)
- 如果是一个数,加入 tempList
- 如果是 ( ,则直接入 operStack(括号内的表达式优先计算)
- 如果是 ) ,则依次弹出 operStack 栈顶的运算符,并压入 tempList ,直到遇到左括号为止,此时将这一对括号丢弃(括号内的表达式优先计算)
- 否则比较当前运算符和栈顶运算符优先级
- 当前运算符优先级 > 栈顶运算符,将当前运算符压入 operStack 栈中(当前运算符优先级较高,先进行运算)
- 当前运算符优先级 <= 栈顶运算符,将 operStack 栈顶运算符取出,压入 tempList 中,再次对新的栈顶元素进行优先级判断(之前的运算符优先级较高,先进行运算)
// 即 ArrayList [1,+,(,(,2,+,3,),*,4,),-,5] =》 ArrayList [1,2,3,+,4,*,+,5,–]
// 方法:将得到的中缀表达式对应的List => 后缀表达式对应的List
public static List<String> parseSuffixExpreesionList(List<String> ls) {
// 定义两个栈
Stack<String> operStack = new Stack<String>(); // 符号栈
// 说明:因为tempList 这个栈,在整个转换过程中,没有pop操作,而且后面我们还需要逆序输出
// 因此比较麻烦,这里我们就不用 Stack<String> 直接使用 List<String> tempList
// Stack<String> tempStack = new Stack<String>(); // 储存中间结果的栈tempStack
List<String> tempList = new ArrayList<String>(); // 储存中间结果的tempList
// 遍历ls
for (String item : ls) {
if (item.matches("\\d+")) { // 如果是一个数,加入tempList
tempList.add(item);
} else if (item.equals("(")) { // 如果是 ( ,则直接入operStack
operStack.push(item);
} else if (item.equals(")")) { // 如果是 ) ,则将括号内的值算出,并压入 tempList)
// 如果是右括号“)”,则依次弹出operStack栈顶的运算符,并压入tempList,直到遇到左括号为止,此时将这一对括号丢弃
while (!operStack.peek().equals("(")) {
tempList.add(operStack.pop());
}
operStack.pop();// !!! 将 ( 弹出 s1栈, 消除小括号
} else { // 否则比较当前运算符和栈顶运算符优先级
// 当item的优先级小于等于operStack栈顶运算符,
// 将operStack栈顶的运算符弹出并加入到tempList中,再次转到(4.1)与operStack中新的栈顶运算符相比较
// 问题:我们缺少一个比较优先级高低的方法
while (operStack.size() != 0 && Operation.getValue(operStack.peek()) >= Operation.getValue(item)) {
tempList.add(operStack.pop());
}
// 还需要将item压入栈
operStack.push(item);
}
}
// 将operStack中剩余的运算符依次弹出并加入tempList
while (operStack.size() != 0) {
tempList.add(operStack.pop());
}
return tempList; // 注意因为是存放到List, 因此按顺序输出就是对应的后缀表达式对应的List
}- 测试代码:
- 将中缀表达式转为对应的 List
- 将中缀表达式 List 转为后缀表达式 List
- 调用逆波兰计算器执行计算
public static void main(String[] args) {
// 完成将一个中缀表达式转成后缀表达式的功能
// 说明
// 1. 1+((2+3)×4)-5 => 转成 1 2 3 + 4 × + 5 –
// 2. 因为直接对str 进行操作,不方便,因此 先将 "1+((2+3)×4)-5" =》 中缀的表达式对应的List
// 即 "1+((2+3)×4)-5" => ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
// 3. 将得到的中缀表达式对应的List => 后缀表达式对应的List
// 即 ArrayList [1,+,(,(,2,+,3,),*,4,),-,5] =》 ArrayList [1,2,3,+,4,*,+,5,–]
String expression = "1+((2+3)*4)-5";// 注意表达式
List<String> infixExpressionList = toInfixExpressionList(expression);
System.out.println("中缀表达式对应的List=" + infixExpressionList); // ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
List<String> suffixExpreesionList = parseSuffixExpreesionList(infixExpressionList);
System.out.println("后缀表达式对应的List" + suffixExpreesionList); // ArrayList [1,2,3,+,4,*,+,5,–]
System.out.printf("expression=%d", calculate(suffixExpreesionList)); // ?
}- 程序运行结果
中缀表达式对应的List=[1, +, (, (, 2, +, 3, ), *, 4, ), -, 5]
后缀表达式对应的List[1, 2, 3, +, 4, *, +, 5, -]
expression=16# 6.4、中缀表达式转后缀表达式完整代码
public class PolandNotation {
public static void main(String[] args) {
// 完成将一个中缀表达式转成后缀表达式的功能
// 说明
// 1. 1+((2+3)×4)-5 => 转成 1 2 3 + 4 × + 5 –
// 2. 因为直接对str 进行操作,不方便,因此 先将 "1+((2+3)×4)-5" =》 中缀的表达式对应的List
// 即 "1+((2+3)×4)-5" => ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
// 3. 将得到的中缀表达式对应的List => 后缀表达式对应的List
// 即 ArrayList [1,+,(,(,2,+,3,),*,4,),-,5] =》 ArrayList [1,2,3,+,4,*,+,5,–]
String expression = "1+((2+3)*4)-5";// 注意表达式
List<String> infixExpressionList = toInfixExpressionList(expression);
System.out.println("中缀表达式对应的List=" + infixExpressionList); // ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
List<String> suffixExpreesionList = parseSuffixExpreesionList(infixExpressionList);
System.out.println("后缀表达式对应的List" + suffixExpreesionList); // ArrayList [1,2,3,+,4,*,+,5,–]
System.out.printf("expression=%d", calculate(suffixExpreesionList)); // ?
}
// 方法:将 中缀表达式转成对应的List
// s="1+((2+3)×4)-5";
public static List<String> toInfixExpressionList(String s) {
// 定义一个List,存放中缀表达式 对应的内容
List<String> ls = new ArrayList<String>();
int i = 0; // 这时是一个指针,用于遍历 中缀表达式字符串
String str; // 对多位数的拼接
char c; // 每遍历到一个字符,就放入到c
do {
// 如果c是一个非数字,我需要加入到ls
if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
ls.add("" + c);
i++; // i需要后移
} else { // 如果是一个数,需要考虑多位数
str = ""; // 先将str 置成"" '0'[48]->'9'[57]
while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
str += c;// 拼接
i++;
}
ls.add(str);
}
} while (i < s.length());
return ls;// 返回
}
// 即 ArrayList [1,+,(,(,2,+,3,),*,4,),-,5] =》 ArrayList [1,2,3,+,4,*,+,5,–]
// 方法:将得到的中缀表达式对应的List => 后缀表达式对应的List
public static List<String> parseSuffixExpreesionList(List<String> ls) {
// 定义两个栈
Stack<String> operStack = new Stack<String>(); // 符号栈
// 说明:因为tempList 这个栈,在整个转换过程中,没有pop操作,而且后面我们还需要逆序输出
// 因此比较麻烦,这里我们就不用 Stack<String> 直接使用 List<String> tempList
// Stack<String> tempStack = new Stack<String>(); // 储存中间结果的栈tempStack
List<String> tempList = new ArrayList<String>(); // 储存中间结果的tempList
// 遍历ls
for (String item : ls) {
if (item.matches("\\d+")) { // 如果是一个数,加入tempList
tempList.add(item);
} else if (item.equals("(")) { // 如果是 ( ,则直接入operStack
operStack.push(item);
} else if (item.equals(")")) { // 如果是 ) ,则将括号内的值算出,并压入 tempList)
// 如果是右括号“)”,则依次弹出operStack栈顶的运算符,并压入tempList,直到遇到左括号为止,此时将这一对括号丢弃
while (!operStack.peek().equals("(")) {
tempList.add(operStack.pop());
}
operStack.pop();// !!! 将 ( 弹出 s1栈, 消除小括号
} else { // 否则比较当前运算符和栈顶运算符优先级
// 当item的优先级小于等于operStack栈顶运算符,
// 将operStack栈顶的运算符弹出并加入到tempList中,再次转到(4.1)与operStack中新的栈顶运算符相比较
// 问题:我们缺少一个比较优先级高低的方法
while (operStack.size() != 0 && Operation.getValue(operStack.peek()) >= Operation.getValue(item)) {
tempList.add(operStack.pop());
}
// 还需要将item压入栈
operStack.push(item);
}
}
// 将operStack中剩余的运算符依次弹出并加入tempList
while (operStack.size() != 0) {
tempList.add(operStack.pop());
}
return tempList; // 注意因为是存放到List, 因此按顺序输出就是对应的后缀表达式对应的List
}
// 完成对逆波兰表达式的运算
/*
* 1)从左至右扫描,将3和4压入堆栈; 2)遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素),计算出3+4的值,得7,再将7入栈; 3)将5入栈;
* 4)接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈; 5)将6入栈; 6)最后是-运算符,计算出35-6的值,即29,由此得出最终结果
*/
public static int calculate(List<String> ls) {
// 创建给栈, 只需要一个栈即可
Stack<String> stack = new Stack<String>();
// 遍历 ls
for (String item : ls) {
// 这里使用正则表达式来取出数
if (item.matches("\\d+")) { // 匹配的是多位数
// 入栈
stack.push(item);
} else {
// pop出两个数,并运算, 再入栈
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
if (item.equals("+")) {
res = num1 + num2;
} else if (item.equals("-")) {
res = num1 - num2;
} else if (item.equals("*")) {
res = num1 * num2;
} else if (item.equals("/")) {
res = num1 / num2;
} else {
throw new RuntimeException("运算符有误");
}
// 把res 入栈
stack.push("" + res);
}
}
// 最后留在stack中的数据是运算结果
return Integer.parseInt(stack.pop());
}
}
//编写一个类 Operation 可以返回一个运算符 对应的优先级
class Operation {
private static int LEFT_BRACKET = 0;
private static int ADD = 1;
private static int SUB = 1;
private static int MUL = 2;
private static int DIV = 2;
// 写一个方法,返回对应的优先级数字
public static int getValue(String operation) {
int result = 0;
switch (operation) {
case "(":
result = LEFT_BRACKET;
break;
case "+":
result = ADD;
break;
case "-":
result = SUB;
break;
case "*":
result = MUL;
break;
case "/":
result = DIV;
break;
default:
System.out.println("不存在该运算符" + operation);
break;
}
return result;
}
}# 7、完整版逆波兰计算器
public class ReversePolishMultiCalc {
/**
* 匹配 + - * / ( ) 运算符
*/
static final String SYMBOL = "\\+|-|\\*|/|\\(|\\)";
static final String LEFT = "(";
static final String RIGHT = ")";
static final String ADD = "+";
static final String MINUS= "-";
static final String TIMES = "*";
static final String DIVISION = "/";
/**
* 加減 + -
*/
static final int LEVEL_01 = 1;
/**
* 乘除 * /
*/
static final int LEVEL_02 = 2;
/**
* 括号
*/
static final int LEVEL_HIGH = Integer.MAX_VALUE;
static Stack<String> stack = new Stack<>();
static List<String> data = Collections.synchronizedList(new ArrayList<String>());
/**
* 去除所有空白符
* @param s
* @return
*/
public static String replaceAllBlank(String s ){
// \\s+ 匹配任何空白字符,包括空格、制表符、换页符等等, 等价于[ \f\n\r\t\v]
return s.replaceAll("\\s+","");
}
/**
* 判断是不是数字 int double long float
* @param s
* @return
*/
public static boolean isNumber(String s){
Pattern pattern = Pattern.compile("^[-\\+]?[.\\d]*$");
return pattern.matcher(s).matches();
}
/**
* 判断是不是运算符
* @param s
* @return
*/
public static boolean isSymbol(String s){
return s.matches(SYMBOL);
}
/**
* 匹配运算等级
* @param s
* @return
*/
public static int calcLevel(String s){
if("+".equals(s) || "-".equals(s)){
return LEVEL_01;
} else if("*".equals(s) || "/".equals(s)){
return LEVEL_02;
}
return LEVEL_HIGH;
}
/**
* 匹配
* @param s
* @throws Exception
*/
public static List<String> doMatch (String s) throws Exception{
if(s == null || "".equals(s.trim())) throw new RuntimeException("data is empty");
if(!isNumber(s.charAt(0)+"")) throw new RuntimeException("data illeagle,start not with a number");
s = replaceAllBlank(s);
String each;
int start = 0;
for (int i = 0; i < s.length(); i++) {
if(isSymbol(s.charAt(i)+"")){
each = s.charAt(i)+"";
//栈为空,(操作符,或者 操作符优先级大于栈顶优先级 && 操作符优先级不是( )的优先级 及是 ) 不能直接入栈
if(stack.isEmpty() || LEFT.equals(each)
|| ((calcLevel(each) > calcLevel(stack.peek())) && calcLevel(each) < LEVEL_HIGH)){
stack.push(each);
}else if( !stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek())){
//栈非空,操作符优先级小于等于栈顶优先级时出栈入列,直到栈为空,或者遇到了(,最后操作符入栈
while (!stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek()) ){
if(calcLevel(stack.peek()) == LEVEL_HIGH){
break;
}
data.add(stack.pop());
}
stack.push(each);
}else if(RIGHT.equals(each)){
// ) 操作符,依次出栈入列直到空栈或者遇到了第一个)操作符,此时)出栈
while (!stack.isEmpty() && LEVEL_HIGH >= calcLevel(stack.peek())){
if(LEVEL_HIGH == calcLevel(stack.peek())){
stack.pop();
break;
}
data.add(stack.pop());
}
}
start = i ; //前一个运算符的位置
}else if( i == s.length()-1 || isSymbol(s.charAt(i+1)+"") ){
each = start == 0 ? s.substring(start,i+1) : s.substring(start+1,i+1);
if(isNumber(each)) {
data.add(each);
continue;
}
throw new RuntimeException("data not match number");
}
}
//如果栈里还有元素,此时元素需要依次出栈入列,可以想象栈里剩下栈顶为/,栈底为+,应该依次出栈入列,可以直接翻转整个stack 添加到队列
Collections.reverse(stack);
data.addAll(new ArrayList<>(stack));
System.out.println(data);
return data;
}
/**
* 算出结果
* @param list
* @return
*/
public static Double doCalc(List<String> list){
Double d = 0d;
if(list == null || list.isEmpty()){
return null;
}
if (list.size() == 1){
System.out.println(list);
d = Double.valueOf(list.get(0));
return d;
}
ArrayList<String> list1 = new ArrayList<>();
for (int i = 0; i < list.size(); i++) {
list1.add(list.get(i));
if(isSymbol(list.get(i))){
Double d1 = doTheMath(list.get(i - 2), list.get(i - 1), list.get(i));
list1.remove(i);
list1.remove(i-1);
list1.set(i-2,d1+"");
list1.addAll(list.subList(i+1,list.size()));
break;
}
}
doCalc(list1);
return d;
}
/**
* 运算
* @param s1
* @param s2
* @param symbol
* @return
*/
public static Double doTheMath(String s1,String s2,String symbol){
Double result ;
switch (symbol){
case ADD : result = Double.valueOf(s1) + Double.valueOf(s2); break;
case MINUS : result = Double.valueOf(s1) - Double.valueOf(s2); break;
case TIMES : result = Double.valueOf(s1) * Double.valueOf(s2); break;
case DIVISION : result = Double.valueOf(s1) / Double.valueOf(s2); break;
default : result = null;
}
return result;
}
public static void main(String[] args) {
//String math = "9+(3-1)*3+10/2";
String math = "12.8 + (2 - 3.55)*4+10/5.0";
try {
doCalc(doMatch(math));
} catch (Exception e) {
e.printStackTrace();
}
}
}# 递归
# 1、递归介绍
# 1.1、递归应用场景
- 看个实际应用场景, 迷宫问题 (回溯), 递归 (Recursion)
# 1.2、递归的概念
- 简单的说:递归就是方法自己调用自己,每次调用时传入不同的变量,递归有助于编程者解决复杂的问题,同时可以让代码变得简洁。
# 1.3、递归调用机制
- 打印问题
- 阶乘问题
// 阶乘问题
public static int factorial(int n) {
if (n == 1) {
return 1;
} else {
return factorial(n - 1) * n;
}
}
# 1.4、递归能解决什么问题
- 各种数学问题如: 8 皇后问题,汉诺塔,阶乘问题,迷宫问题,球和篮子的问题 (google 编程大赛)
- 各种算法中也会使用到递归, 比如快排, 归并排序, 二分查找, 分治算法等.
- 将用栈解决的问题 --> 递归代码比较简洁
# 1.5、递归需遵循的规则
- 执行一个方法时, 就创建一个新的受保护的独立空间 (一个线程有自己独立的一个栈空间,每个方法调用对应着一个栈帧)
- 方法的局部变量是独立的, 不会相互影响,比如 n 变量
- 如果方法中使用的是引用类型变量 (比如数组), 就会共享该引用类型的数据
- 递归必须向退出递归的条件逼近, 否则就是无限递归,出现 StackOverflowError, 死龟了 😃
- 当一个方法执行完毕,或者遇到 return,就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕。
# 2、递归 - 迷宫问题
# 2.1、代码思路
- 使用二维数组
map[][]模拟迷宫 - 约定: 当
map[i][j]为 0 表示该点没有走过;当为 1 表示墙;2 表示通路可以走 ;3 表示该点已经走过,但是走不通 - setWay () 方法用于找路,true 表示该路可以走通,false 表示该路走不通
- 在走迷宫时,需要确定一个策略 (方法) 下 -> 右 -> 上 -> 左,一步一步向前试探,如果该点走不通,再回溯
- 每当走到一个点时,将该点置为 2 ,暂时假设该路能走通,至于到底走不走得通,得看后面有没有找到通路
- 如果后面的路能走通,从最后一个点开始返回,整个 setWay () 递归调用链都返回 true
- 如果后面的路不能走通,那么将当前的点设置为 3 ,表示是死路,走不通,回溯至上一个点,看看其他方向能不能走通
# 2.2、代码实现
- 迷宫问题递归解法
// 使用递归回溯来给小球找路
// 说明
// 1. map 表示地图
// 2. i,j 表示从地图的哪个位置开始出发 (1,1)
// 3. 如果小球能到 map[6][5] 位置,则说明通路找到.
// 4. 约定: 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙 ; 2 表示通路可以走 ; 3 表示该点已经走过,但是走不通
// 5. 在走迷宫时,需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通,再回溯
/**
*
* @param map 表示地图
* @param i 从哪个位置开始找
* @param j
* @return 如果找到通路,就返回true, 否则返回false
*/
public static boolean setWay(int[][] map, int i, int j) {
if (map[6][5] == 2) { // 通路已经找到ok
return true;
} else {
if (map[i][j] == 0) { // 如果当前这个点还没有走过
// 按照策略 下->右->上->左 走
map[i][j] = 2; // 假定该点是可以走通.
if (setWay(map, i + 1, j)) {// 向下走
return true;
} else if (setWay(map, i, j + 1)) { // 向右走
return true;
} else if (setWay(map, i - 1, j)) { // 向上走
return true;
} else if (setWay(map, i, j - 1)) { // 向左走
return true;
} else {
// 说明该点是走不通,是死路
map[i][j] = 3;
return false;
}
} else { // 如果map[i][j] != 0 , 可能是 1, 2, 3
return false;
}
}
}
// 修改找路的策略,改成 上->右->下->左
public static boolean setWay2(int[][] map, int i, int j) {
if (map[6][5] == 2) { // 通路已经找到ok
return true;
} else {
if (map[i][j] == 0) { // 如果当前这个点还没有走过
// 按照策略 上->右->下->左
map[i][j] = 2; // 假定该点是可以走通.
if (setWay2(map, i - 1, j)) {// 向上走
return true;
} else if (setWay2(map, i, j + 1)) { // 向右走
return true;
} else if (setWay2(map, i + 1, j)) { // 向下走
return true;
} else if (setWay2(map, i, j - 1)) { // 向左走
return true;
} else {
// 说明该点是走不通,是死路
map[i][j] = 3;
return false;
}
} else { // 如果map[i][j] != 0 , 可能是 1(墙体), 2(已经走过的格子), 3(已经走过,并且无法走通的格子)
return false;
}
}
}- 测试代码
public static void main(String[] args) {
// 先创建一个二维数组,模拟迷宫
// 地图
int[][] map = new int[8][7];
// 使用1 表示墙
// 上下全部置为1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
// 左右全部置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
// 设置挡板, 1 表示
map[3][1] = 1;
map[3][2] = 1;
map[4][4] = 1;
map[5][4] = 1;
map[6][4] = 1;
map[4][4] = 1;
// 输出地图
System.out.println("地图的情况");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
// 使用递归回溯给小球找路
setWay(map, 1, 1);
// setWay2(map, 1, 1);
// 输出新的地图, 小球走过,并标识过的地图
System.out.println("小球走过,并标识过的 地图的情况");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}- 程序运行结果
地图的情况
1 1 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 1 0 1
1 0 0 0 1 0 1
1 0 0 0 1 0 1
1 1 1 1 1 1 1
小球走过,并标识过的 地图的情况
1 1 1 1 1 1 1
1 2 0 0 0 0 1
1 2 2 2 0 0 1
1 1 1 2 2 2 1
1 3 3 3 1 2 1
1 3 3 3 1 2 1
1 3 3 3 1 2 1
1 1 1 1 1 1 1 - 搞不清逻辑的话,可以自己玩一玩
地图的情况
1 1 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 1 0 1
1 0 0 0 1 0 1
1 0 0 0 1 0 1
1 1 1 1 1 1 1 -
程序执行逻辑分析
- 第一阶段:按照 下 -> 右 -> 上 -> 左 的策略,走入了死胡同
1 1 1 1 1 1 1 1 2 0 0 0 0 1 1 2 2 2 0 0 1 1 1 1 2 0 0 1 1 2 2 2 1 0 1 1 2 2 2 1 0 1 1 2 2 2 1 0 1 1 1 1 1 1 1 1- 第二阶段:开始回溯,标记此路不通
1 1 1 1 1 1 1 1 2 0 0 0 0 1 1 2 2 2 0 0 1 1 1 1 2 0 0 1 1 3 3 3 1 0 1 1 3 3 3 1 0 1 1 3 3 3 1 0 1 1 1 1 1 1 1 1- 寻找到了通往天堂的路径
1 1 1 1 1 1 1 1 2 0 0 0 0 1 1 2 2 2 0 0 1 1 1 1 2 2 2 1 1 3 3 3 1 2 1 1 3 3 3 1 2 1 1 3 3 3 1 2 1 1 1 1 1 1 1 1
# 2.3、思考题
- 求出最短路径(枚举可能的找路策略)
# 2.4、总结
- 刚开始我还觉得很难理解,想了想,这和递归遍历文件夹不也是有相同之处的吗?
- 如果不进入文件夹看看,我就永远不知道这个文件夹里面是否还有子文件和子文件夹,我们需要遍历到一个文件夹的最深处,然后触底反弹
- 如果我没有到达终点,这条路到底通不通,我并不知道,所以我先试探性地走到终点,然后从终点往前回溯?
- 死路咋办?我也是先试探性地往前走,走不通,我回溯到之前的点,再尝试新的走法
# 3、递归 - 八皇后问题 (回溯算法)
# 3.1、八皇后问题介绍
- 八皇后问题, 是一个古老而著名的问题, 是回溯算法的典型案例。 该问题是国际西洋棋棋手马克斯・贝瑟尔于 1848 年提出: 在 8× 8 格的国际象棋上摆放八个皇后, 使其不能互相攻击, 即: 任意两个皇后都不能处于同一行、同一列或同一斜线上, 问有多少种摆法 (92)。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传 (img-g0vK34lS-1596724123044)(第 6 章 递归.assets/image-20200714210026874.png)]
# 3.2、代码思路
- 第一个皇后先放第一行第一列
- 第二个皇后放在第二行第一列、 然后判断是否 OK, 如果不 OK, 继续放在第二列、 第三列、 依次把所有列都放完, 找到一个合适
- 继续第三个皇后, 还是第一列、 第二列…… ,直到第 8 个皇后也能放在一个不冲突的位置, 算是找到了一个正确解
- 当得到一个正确解时, 在栈回退到上一个栈时, 就会开始回溯, 即将第一个皇后, 放到第一列的所有正确解,全部得到
- 然后回头继续第一个皇后放第二列, 后面继续循环执行 1, 2, 3, 4 的步骤
# 3.3、代码实现
-
关于 array 数组的说明:
- 理论上应该创建一个二维数组来表示棋盘, 但是实际上可以通过算法, 用一个一维数组即可解决问题: array [8] =
- array 数组的下标代表皇后所在的行数,array 数组中的值代表皇后所在的列数
- 比如 a [0] = 0 ,则表示第一个皇后在第一行第一列
-
judge (int n) 方法:
- 参数 n :表示当前在放置第 n 个皇后
- 判断是否在同一列:array[i] == array[n]
- 判断是否在同一斜线上:Math.abs(n - i) == Math.abs(array[n] - array[i]) ,即判断行差绝对值与列差绝对值是否相等
-
check (int n) 方法:
- 参数 n :当前要放置第几个皇后(索引从 0 开始,n=8 时表示八皇后放置完毕)
- 当前放置的皇后,需要与之前的皇后位置进行比较,看看冲不冲突,所以需要一个 for 循环:for (int i = 0; i < n; i++){
public class Queue8 {
// 定义一个max表示共有多少个皇后
int max = 8;
// 定义数组array, 保存皇后放置位置的结果,比如 arr = {0 , 4, 7, 5, 2, 6, 1, 3}
int[] array = new int[max];
static int count = 0;
static int judgeCount = 0;
public static void main(String[] args) {
// 测试一把 , 8皇后是否正确
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.printf("一共有%d种解法\n", count);
System.out.printf("一共判断冲突的次数%d次", judgeCount); // 1.5w
}
// 编写一个方法,放置第n个皇后
// 特别注意: check 是 每一次递归时,进入到check中都有 for(int i = 0; i < max; i++),因此会有回溯
private void check(int n) {
if (n == max) { // n = 8 , 其实8个皇后就已经放好,因为索引从 0 开始
print();
return;
}
// 依次放入皇后,并判断是否冲突
for (int i = 0; i < max; i++) {
// 先把当前这个皇后 n , 放到该行的第1列
array[n] = i;
// 判断当放置第n个皇后到i列时,是否冲突
if (judge(n)) { // 不冲突
// 接着放n+1个皇后,即开始递归
check(n + 1);
}
// 如果冲突,就继续执行 array[n] = i; 即将第n个皇后,放置在本行的后移的一个位置
}
}
// 查看当我们放置第n个皇后, 就去检测该皇后是否和前面已经摆放的皇后冲突
/**
*
* @param n 表示第n个皇后
* @return
*/
private boolean judge(int n) {
judgeCount++;
for (int i = 0; i < n; i++) {
// 说明
// 1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
// 2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
// n = 1 放置第 2列 1 n = 1 array[1] = 1
// Math.abs(1-0) == 1 Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1
// 3. 判断是否在同一行, 没有必要,n 每次都在递增
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
// 写一个方法,可以将皇后摆放的位置输出
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}- 程序运行结果
0 4 7 5 2 6 1 3
0 5 7 2 6 3 1 4
0 6 3 5 7 1 4 2
0 6 4 7 1 3 5 2
1 3 5 7 2 0 6 4
1 4 6 0 2 7 5 3
1 4 6 3 0 7 5 2
1 5 0 6 3 7 2 4
1 5 7 2 0 3 6 4
1 6 2 5 7 4 0 3
1 6 4 7 0 3 5 2
1 7 5 0 2 4 6 3
2 0 6 4 7 1 3 5
2 4 1 7 0 6 3 5
2 4 1 7 5 3 6 0
2 4 6 0 3 1 7 5
2 4 7 3 0 6 1 5
2 5 1 4 7 0 6 3
2 5 1 6 0 3 7 4
2 5 1 6 4 0 7 3
2 5 3 0 7 4 6 1
2 5 3 1 7 4 6 0
2 5 7 0 3 6 4 1
2 5 7 0 4 6 1 3
2 5 7 1 3 0 6 4
2 6 1 7 4 0 3 5
2 6 1 7 5 3 0 4
2 7 3 6 0 5 1 4
3 0 4 7 1 6 2 5
3 0 4 7 5 2 6 1
3 1 4 7 5 0 2 6
3 1 6 2 5 7 0 4
3 1 6 2 5 7 4 0
3 1 6 4 0 7 5 2
3 1 7 4 6 0 2 5
3 1 7 5 0 2 4 6
3 5 0 4 1 7 2 6
3 5 7 1 6 0 2 4
3 5 7 2 0 6 4 1
3 6 0 7 4 1 5 2
3 6 2 7 1 4 0 5
3 6 4 1 5 0 2 7
3 6 4 2 0 5 7 1
3 7 0 2 5 1 6 4
3 7 0 4 6 1 5 2
3 7 4 2 0 6 1 5
4 0 3 5 7 1 6 2
4 0 7 3 1 6 2 5
4 0 7 5 2 6 1 3
4 1 3 5 7 2 0 6
4 1 3 6 2 7 5 0
4 1 5 0 6 3 7 2
4 1 7 0 3 6 2 5
4 2 0 5 7 1 3 6
4 2 0 6 1 7 5 3
4 2 7 3 6 0 5 1
4 6 0 2 7 5 3 1
4 6 0 3 1 7 5 2
4 6 1 3 7 0 2 5
4 6 1 5 2 0 3 7
4 6 1 5 2 0 7 3
4 6 3 0 2 7 5 1
4 7 3 0 2 5 1 6
4 7 3 0 6 1 5 2
5 0 4 1 7 2 6 3
5 1 6 0 2 4 7 3
5 1 6 0 3 7 4 2
5 2 0 6 4 7 1 3
5 2 0 7 3 1 6 4
5 2 0 7 4 1 3 6
5 2 4 6 0 3 1 7
5 2 4 7 0 3 1 6
5 2 6 1 3 7 0 4
5 2 6 1 7 4 0 3
5 2 6 3 0 7 1 4
5 3 0 4 7 1 6 2
5 3 1 7 4 6 0 2
5 3 6 0 2 4 1 7
5 3 6 0 7 1 4 2
5 7 1 3 0 6 4 2
6 0 2 7 5 3 1 4
6 1 3 0 7 4 2 5
6 1 5 2 0 3 7 4
6 2 0 5 7 4 1 3
6 2 7 1 4 0 5 3
6 3 1 4 7 0 2 5
6 3 1 7 5 0 2 4
6 4 2 0 5 7 1 3
7 1 3 0 6 4 2 5
7 1 4 2 0 6 3 5
7 2 0 5 1 4 6 3
7 3 0 2 5 1 6 4
一共有92种解法
一共判断冲突的次数15720次# 3.4、总结
- 还是和走迷宫一样,当前摆法行不行,需要摆完第八个皇后我才能知道
- 上面的解法其实是枚举
- 第一个皇后摆在第一行第一列,然后开始试探,第二个皇后摆在哪里,才不会和第一个皇后冲突,第三个皇后摆在哪里,才不会和第二个皇后冲突。。。
- 如果遇到冲突,则把当前正在放置的皇后往后挪一格,如果 8 列都不行,那么就回溯至上一级皇后,让它试着挪一挪
# 排序算法
# 1、排序算法介绍
# 1.1、排序算法的简介
- 排序也称排序算法 (Sort Algorithm), 排序是将一组数据, 依指定的顺序进行排列的过程。
# 1.2、排序算法的分类
- 内部排序:指将需要处理的所有数据都加载到内部存储器 (内存) 中进行排序。
- 外部排序法:数据量过大, 无法全部加载到内存中, 需要借助外部存储 (文件等) 进行排序。
- 常见的排序算法分类
# 2、算法的复杂度
# 2.1、时间复杂度的度量方法
- 事后统计的方法:这种方法可行,但是有两个问题:
- 一是要想对设计的算法的运行性能进行评测, 需要实际运行该程序;
- 二是所得时间的统计量依赖于计算机的硬件、 软件等环境因素,这种方式, 要在同一台计算机的相同状态下运行, 才能比较哪个算法速度更快。
- 事前估算的方法:通过分析某个算法的时间复杂度来判断哪个算法更优
# 2.2、时间频度
- 基本介绍时间频度: 一个算法花费的时间与算法中语句的执行次数成正比例, 哪个算法中语句执行次数多, 它花费时间就多。 一个算法中的语句执行次数称为语句频度或时间频度。 记为 T (n)。 [举例说明]
- 举例说明 - 基本案例:比如计算 1-100 所有数字之和,我们设计两种算法:
- 举例说明 - 忽略常数项:
- 2n+20 和 2n 随着 n 变大, 执行曲线无限接近,20 可以忽略
- 3n+10 和 3n 随着 n 变大, 执行曲线无限接近,10 可以忽略
- 举例说明 - 忽略低次项:
- 2n^2+3n+10 和 2n^2 随着 n 变大,执行曲线无限接近,可以忽略 3n+10
- n^2+5n+20 和 n^2 随着 n 变大,执行曲线无限接近,可以忽略 5n+20
- 举例说明 - 忽略系数:
- 随着 n 值变大, 5n^2+7n 和 3n^2 + 2n , 执行曲线重合,说明 这种情况下,5 和 3 可以忽略。
- 而 n^3+5n 和 6n^3+4n , 执行曲线分离, 说明多少次方式关键
# 2.3、时间复杂度
- 一般情况下, 算法中的基本操作语句的重复执行次数是问题规模 n 的某个函数, 用 T (n) 表示, 若有某个辅助函数 f (n), 使得当 n 趋近于无穷大时, T (n) /f (n) 的极限值为不等于零的常数, 则称 f (n) 是 T (n) 的同数量级函数。记作 T (n)=O ( f (n) ), 称O ( f (n) ) 为算法的渐进时间复杂度, 简称时间复杂度。
- T (n) 不同, 但时间复杂度可能相同。 如: T (n)=n²+7n+6 与 T (n)=3n²+2n+2 它们的 T (n) 不同, 但时间复杂度相同, 都为 O (n²)。
- 计算时间复杂度的方法:
- 用常数 1 代替运行时间中的所有加法常数 T (n)=n²+7n+6 => T (n)=n²+7n+1
- 修改后的运行次数函数中, 只保留最高阶项 T (n)=n²+7n+1 => T (n) = n²
- 去除最高阶项的系数 T (n) = n² => T (n) = n² => O (n²)
# 2.4、常见的时间复杂度
# 2.4.1、常见时间复杂度概述
-
常见时间复杂度
- 常数阶 O (1)
- 对数阶 O (log2n)
- 线性阶 O (n)
- 线性对数阶 O (nlog2n)
- 平方阶 O (n^2)
- 立方阶 O (n^3)
- k 次方阶 O (n^k)
- 指数阶 O (2^n)
-
结论:
- 常见的算法时间复杂度由小到大依次为: Ο (1)<Ο (log2n)<Ο (n)<Ο (nlog2n)<Ο (n2)<Ο (n3)< Ο (nk) < Ο (2n) , 随着问题规模 n 的不断增大, 上述时间复杂度不断增大, 算法的执行效率越低
- 从图中可见, 我们应该尽可能避免使用指数阶的算法
# 2.4.2、常数阶 O (1)
- 无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是 O (1)
- 代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用 O (1) 来表示它的时间复杂度。
# 2.4.3、对数阶 O (log2n)
# 2.4.4、线性阶 O (n)
- 说明:这段代码,for 循环里面的代码会执行 n 遍,因此它消耗的时间是随着 n 的变化而变化的,因此这类代码都可以用 O (n) 来表示它的时间复杂度
# 2.4.5、线性对数阶 O (nlogN)
- 说明:线性对数阶 O (nlogN) 其实非常容易理解,将时间复杂度为 O (logn) 的代码循环 N 遍的话,那么它的时间复杂度就是 n * O (logN),也就是了 O (nlogN)
# 2.4.6、平方阶 O (n²)
- 说明:平方阶 O (n²) 就更容易理解了,如果把 O (n) 的代码再嵌套循环一遍,它的时间复杂度就是 O (n²),这段代码其实就是嵌套了 2 层 n 循环,它的时间复杂度就是 O (n*n),即 O (n²) 如果将其中一层循环的 n 改成 m,那它的时间复杂度就变成了 O (m*n)
# 2.4.7、其他阶
- 立方阶 O (n³)、 K 次方阶 O (n^k)
- 说明: 参考上面的 O (n²) 去理解就好了, O (n³) 相当于三层 n 循环, 其它的类似
# 2.5、平均和最坏时间复杂度
- 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下, 该算法的运行时间。
- 最坏情况下的时间复杂度称最坏时间复杂度。 一般讨论的时间复杂度均是最坏情况下的时间复杂度。 这样做的原因是: 最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限, 这就保证了算法的运行时间不会比最坏情况更长。
- 平均时间复杂度和最坏时间复杂度是否一致, 和算法有关 (如图)。
# 2.6、算法的空间复杂度
- 类似于时间复杂度的讨论, 一个算法的空间复杂度 (Space Complexity) 定义为该算法所耗费的存储空间, 它也是问题规模 n 的函数。
- 空间复杂度 (Space Complexity) 是对一个算法在运行过程中临时占用存储空间大小的量度。 有的算法需要占用的临时工作单元数与解决问题的规模 n 有关, 它随着 n 的增大而增大, 当 n 较大时, 将占用较多的存储单元, 例如快速排序和归并排序算法,基数排序就属于这种情况
- 在做算法分析时, 主要讨论的是时间复杂度。 从用户使用体验上看, 更看重的程序执行的速度。 一些缓存产品 (redis, memcache) 和算法 (基数排序) 本质就是用空间换时间
# 3、冒泡排序
# 3.1、基本介绍
- 冒泡排序(Bubble Sorting) 的基本思想是: 通过对待排序序列从前向后(从下标较小的元素开始),依次比较相邻元素的值, 若发现逆序则交换, 使值较大的元素逐渐从前移向后部, 就象水底下的气泡一样逐渐向上冒。
- 优化:因为排序的过程中, 各元素不断接近自己的位置, 如果一趟比较下来没有进行过交换, 就说明序列有序, 因此要在排序过程中设置一个标志 flag 判断元素是否进行过交换。 从而减少不必要的比较。 (这里说的优化, 可以在冒泡排序写好后, 再进行)
# 3.2、冒泡排序图解
-
第一趟:
- 从数组 arr 第一个元素开始,与其后面一个元素比较大小
- 如果 arr [i] > arr [i+1] ,则交换,将大的元素换到后面去
- 由于是当前元素与其后面一个元素比较大小,所以只需要执行 arr.length - 1 次循环
-
第二趟:
- 从数组 arr 第一个元素开始,与其后面一个元素比较大小
- 由于第一趟排序完成,数组最后一个元素已是最大元素,所以只需要执行 arr.length - 1 - 1 次循环
-
啥时候完成?下面两个条件满足任意一个即可:
- 当其中有一趟排序没有元素交换位置时,说明数组已经有序
- 或:按照上述流程,跑完第 arr.length - 1 趟之后
- 这样来想:5 个元素的数组,最多只需要跑 4 趟
- 为什么最多只需要跑 4 趟?因为跑完 4 趟之后,数组第二个元素已经成为了数组第二小的元素,那么数组自然就是有序数组
- 即数组长度如果为 n ,那么则需要跑 n - 1 趟
-
总结:两层 for 循环
- 第一层 for 循环控制走多少趟:for (int i = 0; i < arr.length - 1; i++) {
- 第二层 for 循环实现针对该趟循环,进行冒泡:for (int j = 0; j < arr.length - 1 - i; j++) {
-
伪代码:
for (int i = 0; i < ; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
// 执行冒泡操作
}
if(/* 该趟没有交换 */) {
// 数组已然有序,跳出循环
}
}# 3.3、代码实现
# 3.3.1、理解冒泡排序
- 上面的例子不好,我们把数组改成:int arr [] = { 3, 9, -1, 10, -2}; 这样更能说明冒泡排序的特点
public static void main(String[] args) {
int arr[] = { 3, 9, -1, 10, -2 };
int temp;
// 为了容量理解,我们把冒泡排序的演变过程,给大家展示
System.out.println("排序前");
System.out.println(Arrays.toString(arr));
// 第一趟排序,就是将最大的数排在倒数第一位
for (int j = 0; j < arr.length - 1; j++) {
// 如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
System.out.println("第一趟排序后的数组");
System.out.println(Arrays.toString(arr));
// 第二趟排序,就是将第二大的数排在倒数第二位
for (int j = 0; j < arr.length - 1 - 1; j++) {
// 如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
System.out.println("第二趟排序后的数组");
System.out.println(Arrays.toString(arr));
// 第三趟排序,就是将第三大的数排在倒数第三位
for (int j = 0; j < arr.length - 1 - 2; j++) {
// 如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
System.out.println("第三趟排序后的数组");
System.out.println(Arrays.toString(arr));
// 第四趟排序,就是将第4大的数排在倒数第4位
for (int j = 0; j < arr.length - 1 - 3; j++) {
// 如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
System.out.println("第四趟排序后的数组");
System.out.println(Arrays.toString(arr));
}- 程序运行结果
排序前
[3, 9, -1, 10, -2]
第一趟排序后的数组
[3, -1, 9, -2, 10]
第二趟排序后的数组
[-1, 3, -2, 9, 10]
第三趟排序后的数组
[-1, -2, 3, 9, 10]
第四趟排序后的数组
[-2, -1, 3, 9, 10]
# 3.3.2、编写冒泡排序
- 测试极端情况
public static void main(String[] args) {
int arr[] = { 1, 2, 3, 4, 5, 6 };
// 为了容量理解,我们把冒泡排序的演变过程,给大家展示
System.out.println("排序前");
System.out.println(Arrays.toString(arr));
bubbleSort(arr);
}
// 将前面额冒泡排序算法,封装成一个方法
public static void bubbleSort(int[] arr) {
// 冒泡排序 的时间复杂度 O(n^2), 自己写出
int temp = 0; // 临时变量
boolean flag = false; // 标识变量,表示是否进行过交换
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
// 如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1]) {
flag = true;
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
System.out.println("第" + (i + 1) + "趟排序后的数组");
System.out.println(Arrays.toString(arr));
if (!flag) { // 在一趟排序中,一次交换都没有发生过
break;
} else {
flag = false; // 重置flag!!!, 进行下次判断
}
}
}- 程序运行结果
排序前
[1, 2, 3, 4, 5, 6]
第1趟排序后的数组
[1, 2, 3, 4, 5, 6]# 3.3.3、测试冒泡排序性能
- 测试代码
public static void main(String[] args) {
// 测试一下冒泡排序的速度O(n^2), 给80000个数据,测试
// 创建要给80000个的随机的数组
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println("排序前的时间是=" + date1Str);
// 测试冒泡排序
bubbleSort(arr);
Date date2 = new Date();
String date2Str = simpleDateFormat.format(date2);
System.out.println("排序后的时间是=" + date2Str);
}
// 将前面额冒泡排序算法,封装成一个方法
public static void bubbleSort(int[] arr) {
// 冒泡排序 的时间复杂度 O(n^2), 自己写出
int temp = 0; // 临时变量
boolean flag = false; // 标识变量,表示是否进行过交换
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
// 如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1]) {
flag = true;
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
if (!flag) { // 在一趟排序中,一次交换都没有发生过
break;
} else {
flag = false; // 重置flag!!!, 进行下次判断
}
}
}- 程序运行结果
排序前的时间是=2020-07-15 11:44:08
排序后的时间是=2020-07-15 11:44:16# 4、选择排序
# 4.1、选择排序基本介绍
- 选择式排序也属于内部排序法, 是从欲排序的数据中, 按指定的规则选出某一元素, 再依规定交换位置后达到排序的目的。
# 4.2、选择排序思想
- 选择排序(select sorting) 也是一种简单的排序方法。 它的基本思想是(n 是数组大小):
- 第一次从 arr [0]~arr [n-1] 中选取最小值,与 arr [0] 交换
- 第二次从 arr [1]~arr [n-1] 中选取最小值, 与 arr [1] 交换
- 第三次从 arr [2]~arr [n-1] 中选取最小值, 与 arr [2] 交换, …,
- 第 i 次从 arr [i-1]~arr [n-1] 中选取最小值, 与 arr [i-1] 交换, …,
- 第 n-1 次从 arr [n-2]~arr [n-1] 中选取最小值,与 arr [n-2] 交换,
- 总共通过 n-1 次, 得到一个按排序码从小到大排列的有序序列。
# 4.3、选择排序图解
-
选择排序流程:
- 第一次循环,默认 arr [0] 是最小的元素,将其与 arr [1]~arr [n-1] 进行比较,找到最小的元素,并与 arr [0] 的位置位置
- 第二次循环,默认 arr [1] 是最小的元素,将其与 arr [2]~arr [n-1] 进行比较,找到最小的元素,并与 arr [1] 的位置位置
- 第 i 次循环,默认 arr [i] 是最小的元素,将其与 arr [i+1]~arr [n-1] 进行比较,找到最小的元素,并与 arr [i] 的位置位置
- 直到循环执行 n - 1 次
-
总结:两层 for 循环
- 第一层 for 循环控制走多少趟:for (int i = 0; i < arr.length - 1; i++) {
- 从数组第一个元素开始,因为每次都是拿当前元素 arr [j] 和其后一个元素 arr [j+1] 进行比较
- 到数组倒数第二个元素结束,将 arr [arr.length - 2] 与 arr [arr.length - 1] 进行比较后,数组就已经是有序数组
- 如果数组大小为 n ,那么执行完第 n - 1 趟时,数组就已经是有序数组
- 第二层 for 循环控制从第几个元素开始执行选择排序:for (int j = i + 1; j < arr.length; j++)
- 每次进入第二层 for 循环时,先假设当前元素 arr [i] 是最小的元素:min = arr[i]; ,并记录最小元素的下标:index = i;
- 然后依次和其后面的元素 arr [j] 比较,如果找到比 arr [i] 小的元素,则更新最小值和最小值的索引:min = arr[j]; index = j ;
- 第一层 for 循环控制走多少趟:for (int i = 0; i < arr.length - 1; i++) {
# 4.4、代码实现
# 4.4.1、理解选择排序
- 一步一步理解选择排序算法
//选择排序
public class SelectSort {
public static void main(String[] args) {
int[] arr = { 101, 34, 119, 1 };
selectSort(arr);
}
// 选择排序
public static void selectSort(int[] arr) {
// 使用逐步推导的方式来,讲解选择排序
// 第1轮
// 原始的数组 : 101, 34, 119, 1
// 第一轮排序 : 1, 34, 119, 101
// 算法 先简单--》 做复杂, 就是可以把一个复杂的算法,拆分成简单的问题-》逐步解决
// 第1轮
int minIndex = 0;
int min = arr[0];
for (int j = 0 + 1; j < arr.length; j++) {
if (min > arr[j]) { // 说明假定的最小值,并不是最小
min = arr[j]; // 重置min
minIndex = j; // 重置minIndex
}
}
// 将最小值,放在arr[0], 即交换
if (minIndex != 0) {
arr[minIndex] = arr[0];
arr[0] = min;
}
System.out.println("第1轮后~~");
System.out.println(Arrays.toString(arr));// 1, 34, 119, 101
// 第2轮
minIndex = 1;
min = arr[1];
for (int j = 1 + 1; j < arr.length; j++) {
if (min > arr[j]) { // 说明假定的最小值,并不是最小
min = arr[j]; // 重置min
minIndex = j; // 重置minIndex
}
}
// 将最小值,放在arr[0], 即交换
if (minIndex != 1) {
arr[minIndex] = arr[1];
arr[1] = min;
}
System.out.println("第2轮后~~");
System.out.println(Arrays.toString(arr));// 1, 34, 119, 101
// 第3轮
minIndex = 2;
min = arr[2];
for (int j = 2 + 1; j < arr.length; j++) {
if (min > arr[j]) { // 说明假定的最小值,并不是最小
min = arr[j]; // 重置min
minIndex = j; // 重置minIndex
}
}
// 将最小值,放在arr[0], 即交换
if (minIndex != 2) {
arr[minIndex] = arr[2];
arr[2] = min;
}
System.out.println("第3轮后~~");
System.out.println(Arrays.toString(arr));// 1, 34, 101, 119
}
}- 程序运行结果
第1轮后~~
[1, 34, 119, 101]
第2轮后~~
[1, 34, 119, 101]
第3轮后~~
[1, 34, 101, 119]# 4.4.2、编写选择排序
- 编写选择排序算法
//选择排序
public class SelectSort {
public static void main(String[] args) {
int[] arr = { 101, 34, 119, 1 };
selectSort(arr);
}
// 选择排序
public static void selectSort(int[] arr) {
// 在推导的过程,我们发现了规律,因此,可以使用for来解决
// 选择排序时间复杂度是 O(n^2)
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
int min = arr[i];
for (int j = i + 1; j < arr.length; j++) {
if (min > arr[j]) { // 说明假定的最小值,并不是最小
min = arr[j]; // 重置min
minIndex = j; // 重置minIndex
}
}
// 将最小值,放在arr[0], 即交换
if (minIndex != i) {
arr[minIndex] = arr[i];
arr[i] = min;
}
System.out.println("第" + (i + 1) + "轮后~~");
System.out.println(Arrays.toString(arr));
}
}
}- 程序运行结果
第1轮后~~
[1, 34, 119, 101]
第2轮后~~
[1, 34, 119, 101]
第3轮后~~
[1, 34, 101, 119]# 4.4.3、测试选择排序性能
- 测试代码
//选择排序
public class SelectSort {
public static void main(String[] args) {
//创建要给80000个的随机的数组
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
Date data1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(data1);
System.out.println("排序前的时间是=" + date1Str);
selectSort(arr);
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
}
// 选择排序
public static void selectSort(int[] arr) {
// 在推导的过程,我们发现了规律,因此,可以使用for来解决
// 选择排序时间复杂度是 O(n^2)
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
int min = arr[i];
for (int j = i + 1; j < arr.length; j++) {
if (min > arr[j]) { // 说明假定的最小值,并不是最小
min = arr[j]; // 重置min
minIndex = j; // 重置minIndex
}
}
// 将最小值,放在arr[0], 即交换
if (minIndex != i) {
arr[minIndex] = arr[i];
arr[i] = min;
}
}
}
}- 程序运行结果
排序前的时间是=2020-07-15 19:59:19
排序前的时间是=2020-07-15 19:59:20# 4.5、总结
- 由于选择排序算法在最内层的 for 循环中,满足
if (min > arr[j]) {条件后,只需要记录最小值和最小值在数组中的索引,无需像冒泡排序那样每次都要执行交换操作,所以选择排序算法的执行速度比冒泡排序算法快一些
# 5、插入排序
# 5.1、插入排序基本介绍
- 插入式排序属于内部排序法, 是对于欲排序的元素以插入的方式找寻该元素的适当位置, 以达到排序的目的。
# 5.2、插入排序思想
- 插入排序(Insertion Sorting) 的基本思想是: 把 n 个待排序的元素看成为一个有序表和一个无序表
- 开始时有序表中只包含一个元素, 无序表中包含有 n-1 个元素, 排序过程中每次从无序表中取出第一个元素, 把它的排序码依次与有序表元素的排序码进行比较, 将它插入到有序表中的适当位置, 使之成为新的有序表
# 5.3、插入排序图解
-
插入排序逻辑:
- 首先,将数组分为两个数组,前部分有序数组,后部分是无序数组,我们的目的就是一点一点取出无序数组中的值,将其放到有序数组中区
- 第一趟:arr [0] 作为有序数组的元素,arr [1] 作为无序数组中第一个元素,将 arr [1] 与 arr [0] 比较,目标是将 arr [1] 插入到有序数组中
- 第一趟:arr [0] 和 arr [1] 作为有序数组的元素,arr [2] 作为无序数组中第一个元素,将 arr [2] 与 arr [0] 和 arr [1] 比较,目标是将 arr [2] 插入到有序数组中
- 第 i 趟:arr [0]~arr [i] 作为有序数组的元素,arr [i+1] 作为无序数组中第一个元素,将 arr [i+1] 与 arr [0]~arr [i] 比较,目标是将 arr [i+1] 插入到有序数组中
- 第 n-1 趟:此时有序数组为 arr [0]~arr [n-2] ,无序数组为 arr [n-1] ,将无序数组中最后一个元素插入到有序数组中即可
- 如何进行插入?
- 假设有个指针(index),指向无序数组中的第一个元素,即 arr [index] 是无序数组中的第一个元素,我们定义一个变量来存储该值:int insertVal = arr [index];,现在要将其插入到前面的有序数组中
- 将 index 前移一步,则指向有序数组最后一个元素,我们定义一个新的变量来存储该指针:insertIndex = index - 1; ,即 arr [insertIndex] 是有序数组最后一个元素
- 我们需要找到一个比 insertVal 小的值,并将 insertVal 插入在该值后面:
- 如果 insertVal > arr [insertIndex] ,执行插入
- 如果 insertVal <arr [insertIndex] ,将有序数组后移,腾出插入空间,insertIndex 指针前移,再看看前一个元素满不满足条件,直到找到插入位置
- 即循环终止条件为找到插入位置,又分为两种情况:
- 在有序数组中间找到插入位置
- insertVal 比有序数组中所有的数都小,插入在数组第一个位置(insertIndex = 0 的情况)
-
总结:两层循环
-
for 循环控制走多少趟:for(int i = 1; i < arr.length; i++) { ,从数组第一个元素开始到数组最后一个元素结束
-
while 循环不断将指针前移,在有序数组中寻找插入位置,并执行插入:
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
-
# 5.4、代码实现
# 5.4.1、理解插入排序
- 理解插入排序算法
public class InsertSort {
public static void main(String[] args) {
int[] arr = { 101, 34, 119, 1 };
insertSort(arr);
}
// 插入排序
public static void insertSort(int[] arr) {
// 使用逐步推导的方式来讲解,便利理解
// 第1轮 {101, 34, 119, 1}; => {34, 101, 119, 1}
// {101, 34, 119, 1}; => {101,101,119,1}
// 定义待插入的数
int insertVal = arr[1];
int insertIndex = 1 - 1; // 即arr[1]的前面这个数的下标
// 给insertVal 找到插入的位置
// 说明
// 1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界
// 2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置
// 3. 就需要将 arr[insertIndex] 后移
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
// 当退出while循环时,说明插入的位置找到, insertIndex + 1
// 举例:理解不了,我们一会 debug
arr[insertIndex + 1] = insertVal;
System.out.println("第1轮插入");
System.out.println(Arrays.toString(arr));
// 第2轮
insertVal = arr[2];
insertIndex = 2 - 1;
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
arr[insertIndex + 1] = insertVal;
System.out.println("第2轮插入");
System.out.println(Arrays.toString(arr));
// 第3轮
insertVal = arr[3];
insertIndex = 3 - 1;
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
arr[insertIndex + 1] = insertVal;
System.out.println("第3轮插入");
System.out.println(Arrays.toString(arr));
}
}- 程序运行结果
第1轮插入
[34, 101, 119, 1]
第2轮插入
[34, 101, 119, 1]
第3轮插入
[1, 34, 101, 119]# 5.4.2、编写插入排序
- 编写插入排序算法
public class InsertSort {
public static void main(String[] args) {
int[] arr = { 101, 34, 119, 1 };
insertSort(arr);
}
// 插入排序
public static void insertSort(int[] arr) {
int insertVal = 0;
int insertIndex = 0;
//使用for循环来把代码简化
for(int i = 1; i < arr.length; i++) {
//定义待插入的数
insertVal = arr[i];
insertIndex = i - 1; // 即arr[1]的前面这个数的下标
// 给insertVal 找到插入的位置
// 说明
// 1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界
// 2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置
// 3. 就需要将 arr[insertIndex] 后移
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
// 当退出while循环时,说明插入的位置找到, insertIndex + 1
// 因为我们找到的元素,即下标为 insertIndex 的元素值比 insertVal 小
// 所以我们要将 insertVal 插入到 insertIndex + 1 的位置
arr[insertIndex + 1] = insertVal;
System.out.println("第"+i+"轮插入");
System.out.println(Arrays.toString(arr));
}
}
}- 程序运行结果
第1轮插入
[34, 101, 119, 1]
第2轮插入
[34, 101, 119, 1]
第3轮插入
[1, 34, 101, 119]# 5.4.3、测试插入排序性能
- 测试插入排序性能
public class InsertSort {
public static void main(String[] args) {
// 创建要给80000个的随机的数组
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("插入排序前");
Date data1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(data1);
System.out.println("排序前的时间是=" + date1Str);
insertSort(arr); // 调用插入排序算法
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
}
// 插入排序
public static void insertSort(int[] arr) {
int insertVal = 0;
int insertIndex = 0;
//使用for循环来把代码简化
for(int i = 1; i < arr.length; i++) {
//定义待插入的数
insertVal = arr[i];
insertIndex = i - 1; // 即arr[1]的前面这个数的下标
// 给insertVal 找到插入的位置
// 说明
// 1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界
// 2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置
// 3. 就需要将 arr[insertIndex] 后移
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
// 当退出while循环时,说明插入的位置找到, insertIndex + 1
// 举例:理解不了,我们一会 debug
//这里我们判断是否需要赋值
arr[insertIndex + 1] = insertVal;
}
}
}- 程序运行结果
插入排序前
排序前的时间是=2020-07-15 21:49:48
排序前的时间是=2020-07-15 21:49:50# 5.5、总结
- 插入排序在寻找插入位置时,需要对数组元素进行整体挪位,所以效率比选择排序稍低
# 6、希尔排序
# 6.1、简单插入排序问题
- 我们看简单的插入排序可能存在的问题,数组 arr = {2, 3, 4, 5, 6, 1} 这时需要插入的数 1 (最小),简单插入排序的过程如下
- 结论:当需要插入的数是较小的数时, 后移的次数明显增多, 对效率有影响
{2,3,4,5,6,6}
{2,3,4,5,5,6}
{2,3,4,4,5,6}
{2,3,3,4,5,6}
{2,2,3,4,5,6}
{1,2,3,4,5,6}# 6.2、希尔排序基本介绍
- 希尔排序是希尔(Donald Shell) 于 1959 年提出的一种排序算法。 希尔排序也是一种插入排序, 它是简单插入排序经过改进之后的一个更高效的版本, 也称为缩小增量排序。
# 6.3、希尔排序基本思想
- 希尔排序按照增量将数组进行分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止
# 6.4、希尔排序图解(交换法)
-
第一次:gap = arr.length/5 = 5 , 将数组分为五组,每个数组元素的索引相差 5
- 如何完成第一次的排序?
- 仔细想想,我们需要用一次循环将每组中的元素排序
- 总共有五组,我们又需要一次循环
- 所以完成每次排序,需要两层循环
- 程序代码如下,把 i ,j 都看作是辅助指针:
- i 与 j 配合使用,可以将指针从数组第一个元素,移动至最后一个元素,目的:把数组遍历一遍
- j 与 i 配合使用,每次都从数组索引 i 处往前遍历,每次向前移动 gap 个位置,然后进行交换(冒泡排序的意思):看看前面的元素有没有比我的值大,如果前面的元素比我的值大,我就要和他交换位置,跑到前面去
// 希尔排序的第1轮排序 // 因为第1轮排序,是将10个数据分成了 5组 for (int i = 5; i < arr.length; i++) { // 遍历各组中所有的元素(共5组,每组有2个元素), 步长5 for (int j = i - 5; j >= 0; j -= 5) { // 如果当前元素大于加上步长后的那个元素,说明交换 if (arr[j] > arr[j + 5]) { temp = arr[j]; arr[j] = arr[j + 5]; arr[j + 5] = temp; } } } - 如何完成第一次的排序?
-
第二次:gap = gap /2 = 2; , 将数组分为两组,每个数组元素的索引相差 2
- 第一组:
- i = 2 时,数组从索引 2 处往前遍历,间隔为 2 :将 arr [0]、arr [2] 排序
- i = 4 时,数组从索引 4 处往前遍历,间隔为 2 :将 arr [0]、arr [2]、arr [4] 排序
- i = 6 时,数组从索引 6 处往前遍历,间隔为 2 :将 arr [0]、arr [2]、arr [4]、arr [6] 排序
- i = 8 时,数组从索引 8 处往前遍历,间隔为 2 :将 arr [0]、arr [2]、arr [4]、arr [6]、arr [8] 排序
- 第二组:
- i = 3 时,数组从索引 3 处往前遍历,间隔为 2 :将 arr [1]、arr [3] 排序
- i = 5 时,数组从索引 5 处往前遍历,间隔为 2 :将 arr [1]、arr [3]、arr [5] 排序
- i = 7 时,数组从索引 7 处往前遍历,间隔为 2 :将 arr [1]、arr [3]、arr [5]、arr [7] 排序
- i = 9 时,数组从索引 9 处往前遍历,间隔为 2 :将 arr [1]、arr [3]、arr [5]、arr [7]、arr [9] 排序
- 第一组:
// 希尔排序的第2轮排序
// 因为第2轮排序,是将10个数据分成了 5/2 = 2组
for (int i = 2; i < arr.length; i++) {
// 遍历各组中所有的元素(共5组,每组有2个元素), 步长5
for (int j = i - 2; j >= 0; j -= 2) {
// 如果当前元素大于加上步长后的那个元素,说明交换
if (arr[j] > arr[j + 2]) {
temp = arr[j];
arr[j] = arr[j + 2];
arr[j + 2] = temp;
}
}
}
System.out.println("希尔排序2轮后=" + Arrays.toString(arr));- 第三次:gap = gap /2 = 1; , 将数组分为一组,每个数组元素的索引相差 1 ,对于交换法而言,这就是异常冒泡排序
- i = 1 时,数组从索引 1 处往前遍历,间隔为 1 :将 arr [0]、arr [1] 排序
- i = 2 时,数组从索引 2 处往前遍历,间隔为 1 :将 arr [0]、arr [1]、arr [2] 排序
- i = 3 时,数组从索引 3 处往前遍历,间隔为 1 :将 arr [0]、arr [1]、arr [2]、arr [3] 排序
- …
// 希尔排序的第3轮排序
// 因为第3轮排序,是将10个数据分成了 2/2 = 1组
for (int i = 1; i < arr.length; i++) {
// 遍历各组中所有的元素(共5组,每组有2个元素), 步长5
for (int j = i - 1; j >= 0; j -= 1) {
// 如果当前元素大于加上步长后的那个元素,说明交换
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
System.out.println("希尔排序3轮后=" + Arrays.toString(arr));-
总结:每次使用循环改变 gap 的值(初始值:数组大小 / 2 ,之后:gap = gap/2),然后在改变 gap 的循环中嵌套上面的双层 for 循环
- 改变 gap :for (int gap = arr.length / 2; gap > 0; gap /= 2) {
- 内层循环:实现对每组数组的排序
for (int i = gap; i < arr.length; i++) { // 遍历各组中所有的元素(共gap组,每组有?个元素), 步长gap for (int j = i - gap; j >= 0; j -= gap) {- 希尔排序伪代码
for (int gap = arr.length / 2; gap > 0; gap /= 2) { for (int i = gap; i < arr.length; i++) { // 遍历各组中所有的元素(共gap组,每组有?个元素), 步长gap for (int j = i - gap; j >= 0; j -= gap) { // 对每组进行冒泡排序 } } }
# 6.5、代码实现
# 6.5.1、理解希尔排序(交换法)
- 理解基于交换法的希尔排序
public class ShellSort {
public static void main(String[] args) {
int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };
shellSort(arr);
}
// 使用逐步推导的方式来编写希尔排序
// 希尔排序时, 对有序序列在插入时采用交换法,
// 思路(算法) ===> 代码
public static void shellSort(int[] arr) {
int temp = 0;
// 希尔排序的第1轮排序
// 因为第1轮排序,是将10个数据分成了 5组
for (int i = 5; i < arr.length; i++) {
// 遍历各组中所有的元素(共5组,每组有2个元素), 步长5
for (int j = i - 5; j >= 0; j -= 5) {
// 如果当前元素大于加上步长后的那个元素,说明交换
if (arr[j] > arr[j + 5]) {
temp = arr[j];
arr[j] = arr[j + 5];
arr[j + 5] = temp;
}
}
}
System.out.println("希尔排序1轮后=" + Arrays.toString(arr));
// 希尔排序的第2轮排序
// 因为第2轮排序,是将10个数据分成了 5/2 = 2组
for (int i = 2; i < arr.length; i++) {
// 遍历各组中所有的元素(共5组,每组有2个元素), 步长5
for (int j = i - 2; j >= 0; j -= 2) {
// 如果当前元素大于加上步长后的那个元素,说明交换
if (arr[j] > arr[j + 2]) {
temp = arr[j];
arr[j] = arr[j + 2];
arr[j + 2] = temp;
}
}
}
System.out.println("希尔排序2轮后=" + Arrays.toString(arr));
// 希尔排序的第3轮排序
// 因为第3轮排序,是将10个数据分成了 2/2 = 1组
for (int i = 1; i < arr.length; i++) {
// 遍历各组中所有的元素(共5组,每组有2个元素), 步长5
for (int j = i - 1; j >= 0; j -= 1) {
// 如果当前元素大于加上步长后的那个元素,说明交换
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
System.out.println("希尔排序3轮后=" + Arrays.toString(arr));
}
}- 程序运行结果
希尔排序1轮后=[3, 5, 1, 6, 0, 8, 9, 4, 7, 2]
希尔排序2轮后=[0, 2, 1, 4, 3, 5, 7, 6, 9, 8]
希尔排序3轮后=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]# 6.5.2、编写希尔排序(交换法)
- 编写基于交换法的希尔排序算法
public class ShellSort {
public static void main(String[] args) {
int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };
shellSort(arr);
}
// 使用逐步推导的方式来编写希尔排序
// 希尔排序时, 对有序序列在插入时采用交换法,
// 思路(算法) ===> 代码
public static void shellSort(int[] arr) {
int temp = 0;
int count = 0;
// 根据前面的逐步分析,使用循环处理
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++) {
// 遍历各组中所有的元素(共gap组,每组有?个元素), 步长gap
for (int j = i - gap; j >= 0; j -= gap) {
// 如果当前元素大于加上步长后的那个元素,说明交换
if (arr[j] > arr[j + gap]) {
temp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = temp;
}
}
}
System.out.println("希尔排序第" + (++count) + "轮 =" + Arrays.toString(arr));
}
}- 程序运行结果
希尔排序第1轮 =[3, 5, 1, 6, 0, 8, 9, 4, 7, 2]
希尔排序第2轮 =[0, 2, 1, 4, 3, 5, 7, 6, 9, 8]
希尔排序第3轮 =[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]# 6.5.3、测试希尔排序(交换法)性能
- 测试基于交换法的希尔排序算法性能
public class ShellSort {
public static void main(String[] args) {
// 创建要给80000个的随机的数组
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("排序前");
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println("排序前的时间是=" + date1Str);
shellSort(arr); // 交换式
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
}
// 使用逐步推导的方式来编写希尔排序
// 希尔排序时, 对有序序列在插入时采用交换法,
// 思路(算法) ===> 代码
public static void shellSort(int[] arr) {
int temp = 0;
int count = 0;
// 根据前面的逐步分析,使用循环处理
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++) {
// 遍历各组中所有的元素(共gap组,每组有?个元素), 步长gap
for (int j = i - gap; j >= 0; j -= gap) {
// 如果当前元素大于加上步长后的那个元素,说明交换
if (arr[j] > arr[j + gap]) {
temp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = temp;
}
}
}
}
}
}- 程序运行结果
排序前
排序前的时间是=2020-07-16 10:22:27
排序前的时间是=2020-07-16 10:22:33- 分析:由于使用交换法实现希尔排序算法,所以基于交换法的希尔排序算法比简单选择排序算法更慢,所以我们一定要编写基于插入法的希尔排序算法
# 6.5.4、编写希尔排序(插入法)
- 编写基于插入法的希尔排序算法:
- 记录当前位置的元素值 int temp = arr[j]; ,从当前元素前一个位置开始,往前寻找,每次移动 gap 个距离
- 如果 temp <arr [j - gap] :
- 将数组元素后移,腾出插入空间:arr[j] = arr[j - gap];
- 然后继续往前找:j -= gap;
- 如果 temp > arr[j - gap] ,找到插入位置,执行插入 arr[j] = temp; ,因为在上一步已经腾出了插入空间,并且将指针 j 前移,所以可直接插入
- 如果 找到数组最前面还是没有找到插入位置:j - gap < 0 ,则证明 temp 需要插入在数组最前面
- 如果 temp <arr [j - gap] :
- 仅仅就是将之前交换法的冒泡操作替换成了插入操作
- 记录当前位置的元素值 int temp = arr[j]; ,从当前元素前一个位置开始,往前寻找,每次移动 gap 个距离
public class ShellSort {
public static void main(String[] args) {
int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };
System.out.println("排序前");
System.out.println(Arrays.toString(arr));
shellSort(arr);
System.out.println("排序前");
System.out.println(Arrays.toString(arr));
}
// 对交换式的希尔排序进行优化->移位法
public static void shellSort(int[] arr) {
// 增量gap, 并逐步的缩小增量
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
// 从第gap个元素,逐个对其所在的组进行直接插入排序
for (int i = gap; i < arr.length; i++) {
int j = i;
int temp = arr[j];
if (arr[j] < arr[j - gap]) {
while (j - gap >= 0 && temp < arr[j - gap]) {
// 移动
arr[j] = arr[j - gap];
j -= gap;
}
// temp 比 arr[j - gap] 大,所以需要插入在 j 的位置
arr[j] = temp;
}
}
}
}
}- 程序运行结果
排序前
[8, 9, 1, 7, 2, 3, 5, 4, 6, 0]
排序前
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]# 6.5.5、测试希尔排序(插入法)性能
- 测试基于插入法的希尔排序算法性能
public class ShellSort {
public static void main(String[] args) {
// 创建要给80000个的随机的数组
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("排序前");
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println("排序前的时间是=" + date1Str);
shellSort(arr); // 交换式
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
}
// 对交换式的希尔排序进行优化->移位法
public static void shellSort(int[] arr) {
// 增量gap, 并逐步的缩小增量
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
// 从第gap个元素,逐个对其所在的组进行直接插入排序
for (int i = gap; i < arr.length; i++) {
int j = i;
int temp = arr[j];
if (arr[j] < arr[j - gap]) {
while (j - gap >= 0 && temp < arr[j - gap]) {
// 移动
arr[j] = arr[j - gap];
j -= gap;
}
// 当退出while后,就给temp找到插入的位置
arr[j] = temp;
}
}
}
}
}- 程序运行结果:1s 都不到,果然快啊
排序前
排序前的时间是=2020-07-16 11:02:20
排序前的时间是=2020-07-16 11:02:20- 八百万个数据的测试结果
排序前
排序前的时间是=2020-07-16 14:38:55
排序前的时间是=2020-07-16 14:38:57# 7、快速排序
# 7.1、快排简介
- 快速排序是由东尼・霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较,但这种状况并不常见。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
- 快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
- 快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
- 快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高!它是处理大数据最快的排序算法之一了。
- 虽然 Worst Case 的时间复杂度达到了 O (n²),但是人家就是优秀,在大多数情况下都比平均时间复杂度为 O (n logn) 的排序算法表现要更好,可是这是为什么呢,我也不知道。好在我的强迫症又犯了,查了 N 多资料终于在《算法艺术与信息学竞赛》上找到了满意的答案:
- 快速排序的最坏运行情况是 O (n²),比如说顺序数列的快排。但它的平摊期望时间是 O (nlogn),且 O (nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O (nlogn) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。
# 7.2、代码思路
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。
- 在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
快排流程分析
以 {25, 84, 21, 47, 15, 27, 68, 35, 20} 数列为例(下面的流程和上面的动图其实不太一样,不过大体思想是一样的)
- 第一趟:val = 25; 先取出来保存着
- {20, 84, 21, 47, 15, 27, 68, 35, 20}
- {20, 84, 21, 47, 15, 27, 68, 35, 84}
- {20, 15, 21, 47, 15, 27, 68, 35, 84}
- {20, 15, 21, 47, 47, 27, 68, 35, 84}
- {20, 15, 21, 25, 47, 27, 68, 35, 84}
- 第二趟:val = 20; 先取出来保存着
- {15, 15, 21}
- {15, 20, 21}
- 以此类推 …
# 7.3、代码实现
# 7.3.1、编写快排算法
- 快排代码
private static void quickSort(int[] arr, int left, int right) {
if (left < right) {
int partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex - 1);
quickSort(arr, partitionIndex + 1, right);
}
}
private static int partition(int[] arr, int left, int right) {
int pivot = arr[left];
//终止while循环以后left和right一定相等的
while (left < right) {
while (left < right && arr[right] >= pivot) {
--right;
}
arr[left] = arr[right];
while (left < right && arr[left] <= pivot) {
++left;
}
arr[right] = arr[left];
}
arr[left] = pivot;
//right可以改为left
return left;
}
- 测试代码
public static void main(String[] args) {
int[] arr = {25, 84, 21, 47, 15, 27, 68, 35, 20};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}- 程序输出
arr=[15, 20, 21, 25, 27, 35, 47, 68, 84]# 7.3.2、测试快速排序性能
- 编测试快速排序算法性能
public class QuickSort {
public static void main(String[] args) {
// 创建要给80000个的随机的数组
int[] arr = new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("排序前");
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println("排序前的时间是=" + date1Str);
quickSort(arr, 0, arr.length - 1); // 交换式
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
}
private static void quickSort(int[] arr, int left, int right) {
if (left < right) {
int partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex - 1);
quickSort(arr, partitionIndex + 1, right);
}
}
private static int partition(int[] arr, int left, int right) {
int pivot = arr[left];
// 终止while循环以后left和right一定相等的
while (left < right) {
while (left < right && arr[right] >= pivot) {
--right;
}
arr[left] = arr[right];
while (left < right && arr[left] <= pivot) {
++left;
}
arr[right] = arr[left];
}
arr[left] = pivot;
// right可以改为left
return left;
}
}- 程序运行结果:卧槽,八百个数据只需要 1s ,甚至可能还不到。。。
排序前
排序前的时间是=2020-08-06 18:43:44
排序前的时间是=2020-08-06 18:43:44# 8、归并排序
# 8.1、归并排序基本介绍
- 归并排序(MERGE-SORT) 是利用归并的思想实现的排序方法, 该算法采用经典的分治(divide-and-conquer)策略
- 分治法将问题分 (divide) 成一些小的问题然后递归求解, 而治 (conquer) 的阶段则将分的阶段得到的各答案 "修补" 在一起, 即分而治之
# 8.2、归并排序思想
- 分 --> 治
# 8.3、归并排序代码思路
- 合并时,其实是拿着原数组(arr)中两个相邻的子数组(arr1、arr2)进行合并,我们使用三个指针,来表示两个子数组在原数组中的位置
- arr [left] ~ arr [mid] 为 arr1
- arr [mid + 1] ~ arr [right] 为 arr2
- 如何合并?
- 首先,需要一个临时的 temp 数组,其大小与原数组 arr 一样
- 定义辅助指针 i 遍历 arr1 ,定义辅助指针 j 遍历 arr2 ,原则就是,把 arr1 和 arr2 中的数往 temp 中放,使得 temp [left] ~ temp [right] 是有序数组
- 最后把 temp 临时数组中的数据拷贝回原数组中(个人认为,最后一下次再拷贝回去就行。。。)
- 如何分?
- 向左递归拆分:mergeSort (arr, left, mid, temp);
- 向右递归拆分:mergeSort (arr, mid + 1, right, temp);
# 8.4、代码实现
# 8.4.1、编写归并排序算法
- 归并排序算法实现代码
public class MergetSort {
public static void main(String[] args) {
int arr[] = { 8, 4, 5, 7, 1, 3, 6, 2 };
int temp[] = new int[arr.length]; // 归并排序需要一个额外空间
mergeSort(arr, 0, arr.length - 1, temp);
System.out.println("归并排序后=" + Arrays.toString(arr));
}
// 分+合方法
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
int mid = (left + right) / 2; // 中间索引
// 向左递归进行分解
mergeSort(arr, left, mid, temp);
// 向右递归进行分解
mergeSort(arr, mid + 1, right, temp);
// 合并
merge(arr, left, mid, right, temp);
}
}
// 合并的方法
/**
*
* @param arr 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 做中转的数组
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left; // 初始化i, 左边有序序列的初始索引
int j = mid + 1; // 初始化j, 右边有序序列的初始索引
int t = 0; // 指向temp数组的当前索引
// (一)
// 先把左右两边(有序)的数据按照规则填充到temp数组
// 直到左右两边的有序序列,有一边处理完毕为止
while (i <= mid && j <= right) {// 继续
// 如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素
// 即将左边的当前元素,填充到 temp数组
// 然后 t++, i++
if (arr[i] <= arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
} else { // 反之,将右边有序序列的当前元素,填充到temp数组
temp[t] = arr[j];
t += 1;
j += 1;
}
}
// (二)
// 把有剩余数据的一边的数据依次全部填充到temp
while (i <= mid) { // 左边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[i];
t += 1;
i += 1;
}
while (j <= right) { // 右边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[j];
t += 1;
j += 1;
}
// (三)
// 将temp数组的元素拷贝到arr
// 注意,并不是每次都拷贝所有
t = 0;
int tempLeft = left; //
// 第一次合并 tempLeft = 0 , right = 1 //第二次: tempLeft = 2 right = 3 //第三次: tL=0 ri=3
// 最后一次 tempLeft = 0 right = 7
while (tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
}- 程序运行结果
归并排序后=[1, 2, 3, 4, 5, 6, 7, 8]# 8.4.2、测试归并排序性能
- 测试归并排序算法的性能
public class MergetSort {
public static void main(String[] args) {
// 测试快排的执行速度
// 创建要给80000个的随机的数组
int[] arr = new int[8000000];
for (int i = 0; i < 8000000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("排序前");
Date data1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(data1);
System.out.println("排序前的时间是=" + date1Str);
int temp[] = new int[arr.length]; // 归并排序需要一个额外空间
mergeSort(arr, 0, arr.length - 1, temp);
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
// System.out.println("归并排序后=" + Arrays.toString(arr));
}
// 分+合方法
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
int mid = (left + right) / 2; // 中间索引
// 向左递归进行分解
mergeSort(arr, left, mid, temp);
// 向右递归进行分解
mergeSort(arr, mid + 1, right, temp);
// 合并
merge(arr, left, mid, right, temp);
}
}
// 合并的方法
/**
*
* @param arr 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 做中转的数组
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left; // 初始化i, 左边有序序列的初始索引
int j = mid + 1; // 初始化j, 右边有序序列的初始索引
int t = 0; // 指向temp数组的当前索引
// (一)
// 先把左右两边(有序)的数据按照规则填充到temp数组
// 直到左右两边的有序序列,有一边处理完毕为止
while (i <= mid && j <= right) {// 继续
// 如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素
// 即将左边的当前元素,填充到 temp数组
// 然后 t++, i++
if (arr[i] <= arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
} else { // 反之,将右边有序序列的当前元素,填充到temp数组
temp[t] = arr[j];
t += 1;
j += 1;
}
}
// (二)
// 把有剩余数据的一边的数据依次全部填充到temp
while (i <= mid) { // 左边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[i];
t += 1;
i += 1;
}
while (j <= right) { // 右边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[j];
t += 1;
j += 1;
}
// (三)
// 将temp数组的元素拷贝到arr
// 注意,并不是每次都拷贝所有
t = 0;
int tempLeft = left; //
// 第一次合并 tempLeft = 0 , right = 1 //第二次: tempLeft = 2 right = 3 //第三次: tL=0 ri=3
// 最后一次 tempLeft = 0 right = 7
while (tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
}- 程序运行结果:八百万数据用了 1s ,也挺快
排序前
排序前的时间是=2020-07-16 16:18:32
排序前的时间是=2020-07-16 16:18:33# 8.5、总结
- 先将数组分为左右两半,先执行左半边递归:
- 首先执行左递归到最深层,条件 if (left < right) 不满足,开始执行合并,合并 {8, 4} 到临时数组 temp 中,变为有序数组 { 4, 8 } ,再拷贝回原数组 arr 中
- 然后执行最深层的右递归,条件 if (left < right) 不满足,开始执行合并,合并 {5, 7} 到临时数组 temp 中,变为有序数组 { 2, 7 } ,再拷贝回原数组 arr 中
- 合并完后,递归回溯至上一节,开始执行合并,合并 {4, 5, 7, 8} 到临时数组 temp 中,变为有序数组 { 4, 5, 7, 8 } ,再拷贝回原数组 arr 中
- 右左半边的递归也是同样的道理
# 9、基数排序
# 9.1、基数排序基本介绍
- 基数排序(radix sort) 属于 “分配式排序” (distribution sort) , 又称 “桶子法” (bucket sort) 或 bin sort, 顾名思义, 它是通过键值的各个位的值, 将要排序的元素分配至某些 “桶” 中, 达到排序的作用
- 基数排序法是属于稳定性的排序, 基数排序法的是效率高的稳定性排序法
- 基数排序 (Radix Sort) 是桶排序的扩展
- 基数排序是 1887 年赫尔曼・何乐礼发明的。 它是这样实现的: 将整数按位数切割成不同的数字, 然后按每个位数分别比较。
# 9.2、基数排序思想
- 将所有待比较数值统一为同样的数位长度, 数位较短的数前面补零。
- 然后, 从最低位开始, 依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
# 9.3、基数排序图解
-
有 10 个桶,对应编号为 0~9
-
步骤
- 第一步:根据原数组 arr 中每个元素的个位数,将其依次放入 0~9 号桶中(每个桶从前往后放),放置完毕后,再将桶中的数据依次取出(每个桶从前往后取),放回原数组 arr 中,这样原数组 arr 中个位数的元素就已经按照顺序排好了
- 第二步:根据原数组 arr 中每个元素的十位数,将其依次放入 0~9 号桶中(每个桶从前往后放),放置完毕后,再将桶中的数据依次取出(每个桶从前往后取),放回原数组 arr 中,这样原数组 arr 中十位数 + 个位数的元素就已经按照顺序排好了
- 第三步:根据原数组 arr 中每个元素的百位数,将其依次放入 0~9 号桶中(每个桶从前往后放),放置完毕后,再将桶中的数据依次取出(每个桶从前往后取),放回原数组 arr 中,这样原数组 arr 中百位数 + 十位数 + 个位数的元素就已经按照顺序排好了
- …
-
何时排序完毕?当数组中最长位数的元素处理完毕,排序完成
-
桶的容量如何确定?假设数组每个元素位数相同,那么单个桶最大容量即为数组容量,我们用一个二维数组来表示桶:
int[][] bucket = new int[10][arr.length]; -
我们如何知道每桶中装了几个元素?这也需要记录,用一个一维数组来记录:
int[] bucketElementCounts = new int[10]; -
总结:
-
假设数组中元素的最长位数为 maxLength ,则处理完 maxLength 位数后,数组排序完毕:*for(int i = 0 , n = 1; i < maxLength; i++, n = 10) {
-
使用一个 for 循环处理原一维数组 arr ,将其放入桶中
for(int j = 0; j < arr.length; j++) {
-
使用两层 for 循环,处理 10 个 桶,将其中的元素放回原一维数组中
for (int k = 0; k < bucketElementCounts.length; k++) {
if (bucketElementCounts[k] != 0) {
for (int l = 0; l < bucketElementCounts[k]; l++) {
-
# 9.4、代码实现
# 9.4.1、理解基数排序
- 逐步分解,理解基数排序算法
public class RadixSort {
public static void main(String[] args) {
int arr[] = { 53, 3, 542, 748, 14, 214};
radixSort(arr);
System.out.println("基数排序后 " + Arrays.toString(arr));
}
//基数排序方法
public static void radixSort(int[] arr) {
// //根据前面的推导过程,我们可以得到最终的基数排序代码
//1. 得到数组中最大的数的位数
int max = arr[0]; //假设第一数就是最大数
for(int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
//定义一个二维数组,表示10个桶, 每个桶就是一个一维数组
//说明
//1. 二维数组包含10个一维数组
//2. 为了防止在放入数的时候,数据溢出,则每个一维数组(桶),大小定为arr.length
//3. 名明确,基数排序是使用空间换时间的经典算法
int[][] bucket = new int[10][arr.length];
//为了记录每个桶中,实际存放了多少个数据,我们定义一个一维数组来记录各个桶的每次放入的数据个数
//可以这里理解
//比如:bucketElementCounts[0] , 记录的就是 bucket[0] 桶的放入数据个数
int[] bucketElementCounts = new int[10];
//第1轮(针对每个元素的个位进行排序处理)
for(int j = 0; j < arr.length; j++) {
//取出每个元素的个位的值
int digitOfElement = arr[j] / 1 % 10;
//放入到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
int index = 0;
//遍历每一桶,并将桶中是数据,放入到原数组
for(int k = 0; k < bucketElementCounts.length; k++) {
//如果桶中,有数据,我们才放入到原数组
if(bucketElementCounts[k] != 0) {
//循环该桶即第k个桶(即第k个一维数组), 放入
for(int l = 0; l < bucketElementCounts[k]; l++) {
//取出元素放入到arr
arr[index++] = bucket[k][l];
}
}
//第l轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!
bucketElementCounts[k] = 0;
}
System.out.println("第1轮,对个位的排序处理 arr =" + Arrays.toString(arr));
//第2轮(针对每个元素的十位进行排序处理)
for (int j = 0; j < arr.length; j++) {
// 取出每个元素的十位的值
int digitOfElement = arr[j] / 10 % 10; //748 / 10 => 74 % 10 => 4
// 放入到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
// 按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
index = 0;
// 遍历每一桶,并将桶中是数据,放入到原数组
for (int k = 0; k < bucketElementCounts.length; k++) {
// 如果桶中,有数据,我们才放入到原数组
if (bucketElementCounts[k] != 0) {
// 循环该桶即第k个桶(即第k个一维数组), 放入
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放入到arr
arr[index++] = bucket[k][l];
}
}
//第2轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!
bucketElementCounts[k] = 0;
}
System.out.println("第2轮,对个位的排序处理 arr =" + Arrays.toString(arr));
//第3轮(针对每个元素的百位进行排序处理)
for (int j = 0; j < arr.length; j++) {
// 取出每个元素的百位的值
int digitOfElement = arr[j] / 100 % 10; // 748 / 100 => 7 % 10 = 7
// 放入到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
// 按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
index = 0;
// 遍历每一桶,并将桶中是数据,放入到原数组
for (int k = 0; k < bucketElementCounts.length; k++) {
// 如果桶中,有数据,我们才放入到原数组
if (bucketElementCounts[k] != 0) {
// 循环该桶即第k个桶(即第k个一维数组), 放入
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放入到arr
arr[index++] = bucket[k][l];
}
}
//第3轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!
bucketElementCounts[k] = 0;
}
System.out.println("第3轮,对个位的排序处理 arr =" + Arrays.toString(arr));
}
}- 程序运行结果
第1轮,对个位的排序处理 arr =[542, 53, 3, 14, 214, 748]
第2轮,对个位的排序处理 arr =[3, 14, 214, 542, 748, 53]
第3轮,对个位的排序处理 arr =[3, 14, 53, 214, 542, 748]
基数排序后 [3, 14, 53, 214, 542, 748]# 9.4.2、编写基数排序
- 编写基数排序算法
public class RadixSort {
public static void main(String[] args) {
int arr[] = { 53, 3, 542, 748, 14, 214 };
radixSort(arr);
System.out.println("基数排序后 " + Arrays.toString(arr));
}
// 基数排序方法
public static void radixSort(int[] arr) {
//根据前面的推导过程,我们可以得到最终的基数排序代码
//1. 得到数组中最大的数的位数
int max = arr[0]; //假设第一数就是最大数
for(int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
//得到最大数是几位数
int maxLength = (max + "").length();
//定义一个二维数组,表示10个桶, 每个桶就是一个一维数组
//说明
//1. 二维数组包含10个一维数组
//2. 为了防止在放入数的时候,数据溢出,则每个一维数组(桶),大小定为arr.length
//3. 名明确,基数排序是使用空间换时间的经典算法
int[][] bucket = new int[10][arr.length];
//为了记录每个桶中,实际存放了多少个数据,我们定义一个一维数组来记录各个桶的每次放入的数据个数
//可以这里理解
//比如:bucketElementCounts[0] , 记录的就是 bucket[0] 桶的放入数据个数
int[] bucketElementCounts = new int[10];
// n=1 表示处理个位,n=10表示处理十位,n=100表示处理百位 ......
for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {
//(针对每个元素的对应位进行排序处理), 第一次是个位,第二次是十位,第三次是百位..
for(int j = 0; j < arr.length; j++) {
//取出每个元素的对应位的值
int digitOfElement = arr[j] / n % 10;
//放入到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
int index = 0;
//遍历每一桶,并将桶中的数据,放入到原数组
for(int k = 0; k < bucketElementCounts.length; k++) {
//如果桶中,有数据,我们才放入到原数组
// 遍历第k个桶(即第k个一维数组), 将桶中的数据放回原数组中
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放入到arr
arr[index++] = bucket[k][l];
}
//第i+1轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!
bucketElementCounts[k] = 0;
}
System.out.println("第"+(i+1)+"轮,对个位的排序处理 arr =" + Arrays.toString(arr));
}
}
}- 程序运行结果
第1轮,对个位的排序处理 arr =[542, 53, 3, 14, 214, 748]
第2轮,对个位的排序处理 arr =[3, 14, 214, 542, 748, 53]
第3轮,对个位的排序处理 arr =[3, 14, 53, 214, 542, 748]
基数排序后 [3, 14, 53, 214, 542, 748]# 9.4.3、测试基数排序性能
- 测试基数排序算法的性能
public class RadixSort {
public static void main(String[] args) {
// 80000000 * 11 * 4 / 1024 / 1024 / 1024 =3.3G
int[] arr = new int[8000000];
for (int i = 0; i < 8000000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("排序前");
Date data1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(data1);
System.out.println("排序前的时间是=" + date1Str);
radixSort(arr);
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
}
// 基数排序方法
public static void radixSort(int[] arr) {
//根据前面的推导过程,我们可以得到最终的基数排序代码
//1. 得到数组中最大的数的位数
int max = arr[0]; //假设第一数就是最大数
for(int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
//得到最大数是几位数
int maxLength = (max + "").length();
//定义一个二维数组,表示10个桶, 每个桶就是一个一维数组
//说明
//1. 二维数组包含10个一维数组
//2. 为了防止在放入数的时候,数据溢出,则每个一维数组(桶),大小定为arr.length
//3. 名明确,基数排序是使用空间换时间的经典算法
int[][] bucket = new int[10][arr.length];
//为了记录每个桶中,实际存放了多少个数据,我们定义一个一维数组来记录各个桶的每次放入的数据个数
//可以这里理解
//比如:bucketElementCounts[0] , 记录的就是 bucket[0] 桶的放入数据个数
int[] bucketElementCounts = new int[10];
// n=1 表示处理个位,n=10表示处理十位,n=100表示处理百位 ......
for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {
//(针对每个元素的对应位进行排序处理), 第一次是个位,第二次是十位,第三次是百位..
for(int j = 0; j < arr.length; j++) {
//取出每个元素的对应位的值
int digitOfElement = arr[j] / n % 10;
//放入到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
int index = 0;
//遍历每一桶,并将桶中的数据,放入到原数组
for(int k = 0; k < bucketElementCounts.length; k++) {
//如果桶中,有数据,我们才放入到原数组
// 遍历第k个桶(即第k个一维数组), 将桶中的数据放回原数组中
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放入到arr
arr[index++] = bucket[k][l];
}
//第i+1轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!
bucketElementCounts[k] = 0;
}
System.out.println("第"+(i+1)+"轮,对个位的排序处理 arr =" + Arrays.toString(arr));
}
}
}- 程序运行结果:可以啊,八百万数据 1s 就排好了,但是太占空间了
排序前
排序前的时间是=2020-07-16 18:16:21
排序前的时间是=2020-07-16 18:16:22# 9.5、基数排序的说明
- 基数排序是对传统桶排序的扩展, 速度很快
- 基数排序是经典的空间换时间的方式, 占用内存很大,当对海量数据排序时, 容易造成 OutOfMemoryError 。
- 基数排序时稳定的。 [注:假定在待排序的记录序列中, 存在多个具有相同的关键字的记录, 若经过排序, 这些记录的相对次序保持不变, 即在原序列中, r [i]=r [j], 且 r [i] 在 r [j] 之前, 而在排序后的序列中, r [i] 仍在 r [j] 之前,则称这种排序算法是稳定的; 否则称为不稳定的]
- 有负数的数组, 我们不用基数排序来进行排序,如果要支持负数, 参考: https://code.i-harness.com/zh-CN/q/e98fa9
# 10、常用排序算法总结和对比
# 10.1、排序算法的比较图
# 10.2、相关术语解释
- 稳定:如果 a 原本在 b 前面, 而 a=b, 排序之后 a 仍然在 b 的前面;
- 不稳定:如果 a 原本在 b 的前面, 而 a=b, 排序之后 a 可能会出现在 b 的后面;
- 内排序: 所有排序操作都在内存中完成;
- 外排序: 由于数据太大, 因此把数据放在磁盘中, 而排序通过磁盘和内存的数据传输才能进行;
- 时间复杂度: 一个算法执行所耗费的时间。
- 空间复杂度: 运行完一个程序所需内存的大小。
- n: 数据规模
- k: “桶” 的个数
- In-place:不占用额外内存
- Out-place:占用额外内存
# 查找算法
# 1、查找算法介绍
- 顺序 (线性) 查找
- 二分查找 / 折半查找
- 插值查找
- 斐波那契查找
# 2、线性查找
- 编写线性查找算法代码
public class SeqSearch {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5 };// 没有顺序的数组
int index = seqSearch(arr, -11);
if (index == -1) {
System.out.println("没有找到到");
} else {
System.out.println("找到,下标为=" + index);
}
}
/**
* 这里我们实现的线性查找是找到一个满足条件的值,就返回
*
* @param arr
* @param value
* @return
*/
public static int seqSearch(int[] arr, int value) {
// 线性查找是逐一比对,发现有相同值,就返回下标
for (int i = 0; i < arr.length; i++) {
if (arr[i] == value) {
return i;
}
}
return -1;
}
}- 程序运行结果
找到,下标为=4# 3、二分查找
# 3.1、二分查找思路
- 二分查找算法的前提:数组必须是有序数组
- 二分查找算法思路分析(递归版):
- 定义两个辅助指针:left、right ,待查找的元素在 arr [left]~arr [right] 之间
- left 初始值为 0 ,right 初始值为 arr.length - 1
- 将数组分成两半:int mid = (left + right) / 2; ,取数组中间值与目标值 findVal 比较
- 如果 mid > findVal ,说明待查找的值在数组左半部分
- 如果 mid < findVal ,说明待查找的值在数组右半部分
- 如果 mid == findVal ,查找到目标值,返回即可
- 何时终止递归?分为两种情况:
- 找到目标值,直接返回目标值 findVal ,结束递归即可
- 未找到目标值:left > right,这样想:如果递归至数组中只有一个数时(left == right),还没有找到目标值,继续执行下一次递归时, left 指针和 right 指针总有一个会再走一步,这时 left 和 right 便会错开,此时 left > right ,返回 -1 并结束递归表示没有找到目标值
# 3.2、代码实现
# 3.2.1、二分查找(单个值)
- 编写二分查找算法:查找到目标值就返回
//注意:使用二分查找的前提是 该数组是有序的.
public class BinarySearch {
public static void main(String[] args) {
int arr[] = { 1, 8, 10, 89, 1000, 1234 };
int resIndex = binarySearch(arr, 0, arr.length - 1, 1000);
System.out.println("resIndex=" + resIndex);
}
// 二分查找算法
/**
*
* @param arr 数组
* @param left 左边的索引
* @param right 右边的索引
* @param findVal 要查找的值
* @return 如果找到就返回下标,如果没有找到,就返回 -1
*/
public static int binarySearch(int[] arr, int left, int right, int findVal) {
// 当 left > right 时,说明递归整个数组,但是没有找到
if (left > right) {
return -1;
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // 向 右递归
return binarySearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 向左递归
return binarySearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
}- 程序运行结果
resIndex=4# 3.2.2、二分查找(所有值)
- 编写二分查找算法:查找到所有目标值,在找到目标值之后,分别往左、往右进行扩散搜索
//注意:使用二分查找的前提是 该数组是有序的.
public class BinarySearch {
public static void main(String[] args) {
int arr[] = { 1, 8, 10, 89, 1000, 1000, 1000, 1234 };
List<Integer> resIndexList = binarySearch(arr, 0, arr.length - 1, 1000);
System.out.println("resIndexList=" + resIndexList);
}
// 完成一个课后思考题:
/*
* 课后思考题: {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中, 有多个相同的数值时,如何将所有的数值都查找到,比如这里的
* 1000
*
* 思路分析 1. 在找到mid 索引值,不要马上返回 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList 4. 将Arraylist返回
*/
public static List<Integer> binarySearch(int[] arr, int left, int right, int findVal) {
// 当 left > right 时,说明递归整个数组,但是没有找到
if (left > right) {
return new ArrayList<Integer>();
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // 向 右递归
return binarySearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 向左递归
return binarySearch(arr, left, mid - 1, findVal);
} else {
// 思路分析
// 1. 在找到mid 索引值,不要马上返回
// 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
// 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
// 4. 将Arraylist返回
List<Integer> resIndexlist = new ArrayList<Integer>();
// 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
int temp = mid - 1;
while (true) {
if (temp < 0 || arr[temp] != findVal) {// 退出
break;
}
// 否则,就temp 放入到 resIndexlist
resIndexlist.add(temp);
temp -= 1; // temp左移
}
resIndexlist.add(mid); //
// 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
temp = mid + 1;
while (true) {
if (temp > arr.length - 1 || arr[temp] != findVal) {// 退出
break;
}
// 否则,就temp 放入到 resIndexlist
resIndexlist.add(temp);
temp += 1; // temp右移
}
return resIndexlist;
}
}
}- 程序运行结果
resIndexList=[4, 5, 6]# 4、插值查找
# 4.1、插值查找基本介绍
- 插值查找算法类似于二分查找, 不同的是插值查找每次从自适应 mid 处开始查找。
# 4.2、插值查找图解
-
将折半查找中的求 mid 索引的公式,low 表示左边索引 left ,high 表示右边索引 right ,key 就是前面我们讲的 findVal
-
图中公式:int mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low]) ;
对应前面的代码公式:
int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left])
-
大致思路和二分查找一样,有如下不同:
-
寻找 mid 公式不同:
int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left]);
-
由于公式中出现 findVal ,所以 findVal 的值不能过大或者过小,否则会引起 mid 过大或过小,引起数组越界问题,
- 添加判断:findVal <arr [left] 和 findVal > arr [right]
- why?findVal = arr [left] 时,mid = left;findVal = arr [right] 时,mid = right;
-
# 4.3、代码实现
- 编写插值查找算法
public class InsertValueSearch {
public static void main(String[] args) {
int [] arr = new int[100];
for(int i = 0; i < 100; i++) {
arr[i] = i + 1;
}
int index = insertValueSearch(arr, 0, arr.length - 1, 1);
System.out.println("index = " + index);
}
//编写插值查找算法
//说明:插值查找算法,也要求数组是有序的
/**
*
* @param arr 数组
* @param left 左边索引
* @param right 右边索引
* @param findVal 查找值
* @return 如果找到,就返回对应的下标,如果没有找到,返回-1
*/
public static int insertValueSearch(int[] arr, int left, int right, int findVal) {
System.out.println("插值查找次数~~");
//注意:findVal < arr[left] 和 findVal > arr[right] 必须需要,否则我们得到的 mid 可能越界
// findVal < arr[left] :说明待查找的值比数组中最小的元素都小
// findVal > arr[right] :说明待查找的值比数组中最大的元素都大
if (left > right || findVal < arr[left] || findVal > arr[right]) {
return -1;
}
// 求出mid, 自适应,额,这不就是一次函数吗
// findVal = arr[left] 时,mid = left
// findVal = arr[right] 时,mid = right
int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
int midVal = arr[mid];
if (findVal > midVal) { // 说明应该向右边递归
return insertValueSearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 说明向左递归查找
return insertValueSearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
}- 程序运行结果
插值查找次数~~
index = 0# 4.4、总结
- 对于数据量较大,关键字分布比较均匀(最好是线性分布)的查找表来说,采用插值查找,速度较快
- 关键字分布不均匀的情况下, 该方法不一定比折半查找要好
# 5、斐波那契查找
# 5.1、斐波那契数列
- 黄金分割点是指把一条线段分割为两部分, 使其中一部分与全长之比等于另一部分与这部分之比。 取其前三位数字的近似值是 0.618。 由于按此比例设计的造型十分美丽, 因此称为黄金分割, 也称为中外比。 这是一个神奇的数字, 会带来意想不到的效果。
- 斐波那契数列 {1, 1, 2, 3, 5, 8, 13, 21, 34, 55} 发现斐波那契数列的两个相邻数的比例, 无限接近 黄金分割值 0.618
# 5.2、斐波那契查找介绍
-
那为什么一定要等分呐?能不能进行 “黄金分割”?也就是 mid = left+0.618 (right-left) ,当然 mid 要取整数。如果这样查找,时间复杂性是多少?也许你还可以编程做个试验,比较一下二分法和 “黄金分割” 法的执行效率。
-
斐波那契查找算法又称为黄金分割法查找算法,斐波那契查找原理与前两种相似, 仅仅改变了中间结点(mid) 的位置,mid 不再是中间或由插值计算得到,而是位于黄金分割点附近, 即 mid = low + F (k-1) - 1
-
对 F (k)-1 的理解
- 由斐波那契数列 F [k]=F [k-1]+F [k-2] 的性质, 可以得到
F[k]-1) =(F[k-1]-1) +(F[k-2]-1) + 1- 该式说明:只要顺序表的长度为 F [k]-1, 则可以将该表分成长度为 F [k-1]-1 和 F [k-2]-1 的两段 ,即如图所示。 从而中间位置为 mid=low+F (k-1)-1 ,类似的, 每一子段也可以用相同的方式分割
- 但顺序表长度 n 不一定刚好等于 F [k]-1, 所以需要将原来的顺序表长度 n 增加至 F [k]-1。 这里的 k 值只要能使得 F [k]-1 恰好大于或等于 n 即可
- 为什么数组总长度是 F (k) - 1 ,而不是 F (k) ?因为凑成 F (k-1) 才能找出中间值,如果数组长度为 F (k) ,而 F (k) = F (k-1) + F (k-2) ,咋个找中间值嘞?
- 为什么数组左边的长度是 F (k-1) - 1 ,数组右边的长度是 F (k-2) - 1 ?就拿个斐波那契数列来说:{ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 } ,54 = 33 + 20 + 1 ,左边是不是 F (k-1) - 1 ,右边是不是 F (k-2) - 1 ,也恰好空出了一个中间值~~~
# 5.3、斐波那契查找思路
- 先根据原数组大小,计算斐波那契数列的得 k 值
- 数组扩容条件是:增大 k 值(索引从 0 开始),使得数组长度刚好大于或者等于斐波那契数列中的 F [k]-1 ,我们定义临时数组 temp ,temp 后面为 0 的元素都按照数组最大元素值填充
- 何时终止斐波那契查找?
- 找到目标值:直接返回目标值索引
- 没有找到目标值:low 指针和 high 指针相等或者擦肩而过,即 low >= high
- 为什么 low == high 时需要单独拎出来?
- low == high 时说明此时数组中只剩下一个元素(a [low] 或者 a [high])没有与目标值比较,并且此时 k 有可能等于 0 ,无法执行 mid = low + f [k - 1] - 1; 操作(k - 1 将导致数组越界)
- 解决办法:我们在程序的最后,将 a [low] 或者 a [high] 单独与目标值 value 进行比较即可,我是通过 Debug 解决数组越界异常的,我并没有想明白,但是不把 low == high 单独拎出来,就会抛异常,哎,烧脑壳~~~改天再想
- mid 值怎么定?mid = low + f[k - 1] - 1 :用黄金分割点确定 mid 的值
- 左右两条路,你怎么选?
- key <temp [mid] :目标值在黄金分割点的左边,看上面的图,应该是 k -= 1;
- key > temp [mid] :目标值在黄金分割点的右边,看上面的图,应该是 k -= 2;
- key = temp [mid] :找到目标值,因为数组经历过扩容,后面的值其实有些是多余的,mid 可能会越界(相对于原数组来说)
- mid <= high :证明 mid 索引在原数组中,返回 mid
- mid > high 时,证明 mid 索引已经越界(相对于原数组来说),返回 high
# 5.4、代码实现
- 编写斐波那契查找算法
public class FibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5 };
System.out.println("index=" + fibSearch(arr, 5));
}
// 因为后面我们mid=low+F(k-1)-1,需要使用到斐波那契数列,因此我们需要先获取到一个斐波那契数列
// 非递归方法得到一个斐波那契数列
public static int[] fib() {
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
// 编写斐波那契查找算法
// 使用非递归的方式编写算法
/**
*
* @param a 数组
* @param key 我们需要查找的关键码(值)
* @return 返回对应的下标,如果没有-1
*/
public static int fibSearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
int k = 0; // 表示斐波那契分割数值的下标
int mid = 0; // 存放mid值
int f[] = fib(); // 获取到斐波那契数列
// 获取到斐波那契分割数值的下标
while (high > f[k] - 1) {
k++;
}
// 因为 f[k] 值 可能大于 a 的 长度,因此我们需要使用Arrays类,构造一个新的数组,并指向temp[]
// 不足的部分会使用0填充
int[] temp = Arrays.copyOf(a, f[k]);
// 实际上需求使用a数组最后的数填充 temp
// 举例:
// temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234,
// 1234,}
for (int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
// 使用while来循环处理,找到我们的数 key
while (low < high) { // 只要这个条件满足,就可以找
mid = low + f[k - 1] - 1;
if (key < temp[mid]) { // 我们应该继续向数组的前面查找(左边)
high = mid - 1;
// 为甚是 k--
// 说明
// 1. 全部元素 = 前面的元素 + 后边元素
// 2. f[k] = f[k-1] + f[k-2]
// 因为 前面有 f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]
// 即 在 f[k-1] 的前面继续查找 k--
// 即下次循环 mid = f[k-1-1]-1
k--;
} else if (key > temp[mid]) { // 我们应该继续向数组的后面查找(右边)
low = mid + 1;
// 为什么是k -=2
// 说明
// 1. 全部元素 = 前面的元素 + 后边元素
// 2. f[k] = f[k-1] + f[k-2]
// 3. 因为后面我们有f[k-2] 所以可以继续拆分 f[k-1] = f[k-3] + f[k-4]
// 4. 即在f[k-2] 的前面进行查找 k -=2
// 5. 即下次循环 mid = f[k - 1 - 2] - 1
k -= 2;
} else { // 找到
// 需要确定,返回的是哪个下标
if (mid <= high) {
return mid;
} else {
return high;
}
}
}
if(a[low]==key) {
return low;
}
else {
return -1;
}
}
}- 程序运行结果
index=4# 哈希表
# 1、Google 上机题
- 看一个实际需求, google 公司的一个上机题:
- 有一个公司,当有新的员工来报道时,要求将该员工的信息加入 (id, 性别,年龄,住址…),当输入该员工的 id 时,要求查找到该员工的所有信息
- 要求:不使用数据库,尽量节省内存,速度越快越好 => 哈希表 (散列)
# 2、哈希表基本介绍
- 散列表(Hash table, 也叫哈希表) ,是根据关键码值 (Key value) 而直接进行访问的数据结构。
- 它通过把关键码值映射到表中一个位置来访问记录, 以加快查找的速度。 这个映射函数叫做散列函数, 存放记录的数组叫做散列表。
- 哈希表的核心:private EmpLinkedList[] empLinkedListArray;
- 哈希表编程思路:
- 先根据对象的信息将其散列,得到 hashCode
- 根据对象的 hashCode 值,找到对应的数组下标,其实就是找到存储对象的链表
- 在链表中进行相应的增删改查操作
# 3、代码实现
# 3.1、Emp 节点
//表示一个雇员
class EmpNode {
public int id;
public String name;
public EmpNode next; // next 默认为 null
public EmpNode(int id, String name) {
super();
this.id = id;
this.name = name;
}
}# 3.2、Emp 链表
- head 是首指针(指向真正存放数据的节点),不是头指针
//创建EmpLinkedList ,表示链表
class EmpLinkedList {
// 首指针,指向第一个EmpNode,因此我们这个链表的head 是直接指向第一个EmpNode
private EmpNode head; // 默认null
// 添加雇员到链表
// 说明
// 1. 假定,当添加雇员时,id 是自增长,即id的分配总是从小到大
// 因此我们将该雇员直接加入到本链表的最后即可
public void add(EmpNode empNode) {
// 如果是添加第一个雇员
if (head == null) {
head = empNode;
return;
}
// 如果不是第一个雇员,则使用一个辅助的指针,帮助定位到最后
EmpNode curEmp = head;
while (true) {
if (curEmp.next == null) {// 说明到链表最后
break;
}
curEmp = curEmp.next; // 后移
}
// 退出时直接将emp 加入链表
curEmp.next = empNode;
}
// 遍历链表的雇员信息
public void list(int no) {
if (head == null) { // 说明链表为空
System.out.println("第 " + (no + 1) + " 链表为空");
return;
}
System.out.print("第 " + (no + 1) + " 链表的信息为");
EmpNode curEmp = head; // 辅助指针
while (true) {
System.out.printf(" => id=%d name=%s ", curEmp.id, curEmp.name);
if (curEmp.next == null) {// 说明curEmp已经是最后结点
break;
}
curEmp = curEmp.next; // 后移,遍历
}
System.out.println();
}
// 根据id查找雇员
// 如果查找到,就返回Emp, 如果没有找到,就返回null
public EmpNode findEmpById(int id) {
// 判断链表是否为空
if (head == null) {
System.out.println("链表为空");
return null;
}
// 辅助指针
EmpNode curEmp = head;
while (true) {
if (curEmp.id == id) {// 找到
break;// 这时curEmp就指向要查找的雇员
}
curEmp = curEmp.next;// 后移
// 退出
if (curEmp == null) {// 说明遍历当前链表没有找到该雇员
break;
}
}
return curEmp;
}
}# 3.3、Emp 哈希表
//创建HashTab 管理多条链表
class HashTab {
private EmpLinkedList[] empLinkedListArray;
private int size; // 表示有多少条链表
// 构造器
public HashTab(int size) {
this.size = size;
// 初始化empLinkedListArray
empLinkedListArray = new EmpLinkedList[size];
for (int i = 0; i < size; i++) {
empLinkedListArray[i] = new EmpLinkedList();
}
}
// 添加雇员
public void add(EmpNode empNode) {
// 根据员工的id ,得到该员工应当添加到哪条链表
int empLinkedListNO = hashFun(empNode.id);
// 将emp 添加到对应的链表中
empLinkedListArray[empLinkedListNO].add(empNode);
}
// 遍历所有的链表,遍历hashtab
public void list() {
for (int i = 0; i < size; i++) {
empLinkedListArray[i].list(i);
}
}
// 根据输入的id,查找雇员
public void findEmpById(int id) {
// 使用散列函数确定到哪条链表查找
int empLinkedListNO = hashFun(id);
EmpNode empNode = empLinkedListArray[empLinkedListNO].findEmpById(id);
if (empNode != null) {// 找到
System.out.printf("在第%d条链表中找到 雇员 id = %d\n", (empLinkedListNO + 1), id);
} else {
System.out.println("在哈希表中,没有找到该雇员~");
}
}
// 编写散列函数, 使用一个简单取模法
public int hashFun(int id) {
return id % size;
}
}# 3.4、代码测试
- 测试代码
public class HashTabDemo {
public static void main(String[] args) {
// 创建哈希表
HashTab hashTab = new HashTab(7);
// 写一个简单的菜单
String key = "";
Scanner scanner = new Scanner(System.in);
while (true) {
System.out.println("add: 添加雇员");
System.out.println("list: 显示雇员");
System.out.println("find: 查找雇员");
System.out.println("exit: 退出系统");
System.out.println();
key = scanner.next();
switch (key) {
case "add":
System.out.println("输入id");
int id = scanner.nextInt();
System.out.println("输入名字");
String name = scanner.next();
// 创建 雇员
EmpNode empNode = new EmpNode(id, name);
hashTab.add(empNode);
break;
case "list":
hashTab.list();
break;
case "find":
System.out.println("请输入要查找的id");
id = scanner.nextInt();
hashTab.findEmpById(id);
break;
case "exit":
scanner.close();
System.exit(0);
default:
break;
}
}
}
}- 程序运行结果
add: 添加雇员
list: 显示雇员
find: 查找雇员
exit: 退出系统
add
输入id
1
输入名字
Heygo
add: 添加雇员
list: 显示雇员
find: 查找雇员
exit: 退出系统
add
输入id
2
输入名字
Oneby
add: 添加雇员
list: 显示雇员
find: 查找雇员
exit: 退出系统
add
输入id
8
输入名字
NiuNiu
add: 添加雇员
list: 显示雇员
find: 查找雇员
exit: 退出系统
list
第 1 链表为空
第 2 链表的信息为 => id=1 name=Heygo => id=8 name=NiuNiu
第 3 链表的信息为 => id=2 name=Oneby
第 4 链表为空
第 5 链表为空
第 6 链表为空
第 7 链表为空
add: 添加雇员
list: 显示雇员
find: 查找雇员
exit: 退出系统
find
请输入要查找的id
1
在第2条链表中找到 雇员 id = 1
add: 添加雇员
list: 显示雇员
find: 查找雇员
exit: 退出系统
find
请输入要查找的id
8
在第2条链表中找到 雇员 id = 8
add: 添加雇员
list: 显示雇员
find: 查找雇员
exit: 退出系统
find
请输入要查找的id
9
在哈希表中,没有找到该雇员~
add: 添加雇员
list: 显示雇员
find: 查找雇员
exit: 退出系统# 3.5、课后练习
- 实现员工的删除
# 4、Emp 哈希表全部代码
public class HashTabDemo {
public static void main(String[] args) {
// 创建哈希表
HashTab hashTab = new HashTab(7);
// 写一个简单的菜单
String key = "";
Scanner scanner = new Scanner(System.in);
while (true) {
System.out.println("add: 添加雇员");
System.out.println("list: 显示雇员");
System.out.println("find: 查找雇员");
System.out.println("exit: 退出系统");
System.out.println();
key = scanner.next();
switch (key) {
case "add":
System.out.println("输入id");
int id = scanner.nextInt();
System.out.println("输入名字");
String name = scanner.next();
// 创建 雇员
EmpNode empNode = new EmpNode(id, name);
hashTab.add(empNode);
break;
case "list":
hashTab.list();
break;
case "find":
System.out.println("请输入要查找的id");
id = scanner.nextInt();
hashTab.findEmpById(id);
break;
case "exit":
scanner.close();
System.exit(0);
default:
break;
}
}
}
}
//创建HashTab 管理多条链表
class HashTab {
private EmpLinkedList[] empLinkedListArray;
private int size; // 表示有多少条链表
// 构造器
public HashTab(int size) {
this.size = size;
// 初始化empLinkedListArray
empLinkedListArray = new EmpLinkedList[size];
for (int i = 0; i < size; i++) {
empLinkedListArray[i] = new EmpLinkedList();
}
}
// 添加雇员
public void add(EmpNode empNode) {
// 根据员工的id ,得到该员工应当添加到哪条链表
int empLinkedListNO = hashFun(empNode.id);
// 将emp 添加到对应的链表中
empLinkedListArray[empLinkedListNO].add(empNode);
}
// 遍历所有的链表,遍历hashtab
public void list() {
for (int i = 0; i < size; i++) {
empLinkedListArray[i].list(i);
}
}
// 根据输入的id,查找雇员
public void findEmpById(int id) {
// 使用散列函数确定到哪条链表查找
int empLinkedListNO = hashFun(id);
EmpNode empNode = empLinkedListArray[empLinkedListNO].findEmpById(id);
if (empNode != null) {// 找到
System.out.printf("在第%d条链表中找到 雇员 id = %d\n", (empLinkedListNO + 1), id);
} else {
System.out.println("在哈希表中,没有找到该雇员~");
}
}
// 编写散列函数, 使用一个简单取模法
public int hashFun(int id) {
return id % size;
}
}
//表示一个雇员
class EmpNode {
public int id;
public String name;
public EmpNode next; // next 默认为 null
public EmpNode(int id, String name) {
super();
this.id = id;
this.name = name;
}
}
//创建EmpLinkedList ,表示链表
class EmpLinkedList {
// 首指针,指向第一个EmpNode,因此我们这个链表的head 是直接指向第一个EmpNode
private EmpNode head; // 默认null
// 添加雇员到链表
// 说明
// 1. 假定,当添加雇员时,id 是自增长,即id的分配总是从小到大
// 因此我们将该雇员直接加入到本链表的最后即可
public void add(EmpNode empNode) {
// 如果是添加第一个雇员
if (head == null) {
head = empNode;
return;
}
// 如果不是第一个雇员,则使用一个辅助的指针,帮助定位到最后
EmpNode curEmp = head;
while (true) {
if (curEmp.next == null) {// 说明到链表最后
break;
}
curEmp = curEmp.next; // 后移
}
// 退出时直接将emp 加入链表
curEmp.next = empNode;
}
// 遍历链表的雇员信息
public void list(int no) {
if (head == null) { // 说明链表为空
System.out.println("第 " + (no + 1) + " 链表为空");
return;
}
System.out.print("第 " + (no + 1) + " 链表的信息为");
EmpNode curEmp = head; // 辅助指针
while (true) {
System.out.printf(" => id=%d name=%s ", curEmp.id, curEmp.name);
if (curEmp.next == null) {// 说明curEmp已经是最后结点
break;
}
curEmp = curEmp.next; // 后移,遍历
}
System.out.println();
}
// 根据id查找雇员
// 如果查找到,就返回Emp, 如果没有找到,就返回null
public EmpNode findEmpById(int id) {
// 判断链表是否为空
if (head == null) {
System.out.println("链表为空");
return null;
}
// 辅助指针
EmpNode curEmp = head;
while (true) {
if (curEmp.id == id) {// 找到
break;// 这时curEmp就指向要查找的雇员
}
curEmp = curEmp.next;// 后移
// 退出
if (curEmp == null) {// 说明遍历当前链表没有找到该雇员
break;
}
}
return curEmp;
}
}# 树结构的基础部分
# 1、二叉树
# 1.1、为什么需要二叉树
# 1.1.1、数组存储方式的分析
- 优点: 通过下标方式访问元素, 速度快。 对于有序数组, 还可使用二分查找提高检索速度
- 缺点: 如果要检索具体某个值, 或者插入值 (按一定顺序) 会整体移动,效率较低
# 1.1.2、链式存储方式的分析
- 优点: 在一定程度上对数组存储方式有优化 (比如: 插入一个数值节点, 只需要将插入节点, 链接到链表中即可,删除效率也很好)。
- 缺点: 在进行检索时, 效率仍然较低, 比如 (检索某个值, 需要从头节点开始遍历)
# 1.1.3、树存储方式的分析
- 能提高数据存储, 读取的效率,比如利用 二叉排序树 (Binary Sort Tree), 既可以保证数据的检索速度, 同时也可以保证数据的插入, 删除, 修改的速度。 【示意图,后面详讲】
# 1.2、树的常用术语
- 节点
- 根节点
- 父节点
- 子节点
- 叶子节点 (没有子节点的节点)
- 节点的权 (节点值)
- 路径 (从 root 节点找到该节点的路线)
- 层
- 子树
- 树的高度 (最大层数)
- 森林:多颗子树构成森林
# 1.3、二叉树的概念
- 树有很多种, 每个节点最多只能有两个子节点的一种形式称为二叉树,二叉树的子节点分为左节点和右节点
- 如果该二叉树的所有叶子节点都在最后一层, 并且结点总数 = 2^n -1, n 为层数, 则我们称为满二叉树
- 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层, 而且最后一层的叶子节点在左边连续, 倒数第二层的叶子节点在右边连续, 我们称为完全二叉树
# 1.4、二叉树的遍历
# 1.4.1、代码思路
- 前序遍历: 先输出父节点, 再遍历左子树和右子树
- 中序遍历:先遍历左子树, 再输出父节点, 再遍历右子树
- 后序遍历:先遍历左子树, 再遍历右子树, 最后输出父节点
# 1.4.2、前 中 后序遍历
- 定义二叉树节点
//先创建 HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; // 默认null
private HeroNode right; // 默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
// 编写前序遍历的方法
public void preOrder() {
System.out.println(this); // 先输出父结点
// 递归向左子树前序遍历
if (this.left != null) {
this.left.preOrder();
}
// 递归向右子树前序遍历
if (this.right != null) {
this.right.preOrder();
}
}
// 中序遍历
public void infixOrder() {
// 递归向左子树中序遍历
if (this.left != null) {
this.left.infixOrder();
}
// 输出父结点
System.out.println(this);
// 递归向右子树中序遍历
if (this.right != null) {
this.right.infixOrder();
}
}
// 后序遍历
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
}- 定义二叉树:二叉树需要一个根节点 root 作为整个树的入口
//定义 BinaryTree 二叉树
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
// 前序遍历
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
// 中序遍历
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
// 后序遍历
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
}# 1.4.3、代码测试
- 测试代码
public static void main(String[] args) {
// 先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
// 创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
// 说明,我们先手动创建该二叉树,后面我们学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
// 测试
System.out.println("前序遍历"); // 1,2,3,5,4
binaryTree.preOrder();
// 测试
System.out.println("中序遍历");
binaryTree.infixOrder(); // 2,1,5,3,4
System.out.println("后序遍历");
binaryTree.postOrder(); // 2,5,4,3,1
}
- 程序运行结果
前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
HeroNode [no=3, name=卢俊义]
HeroNode [no=5, name=关胜]
HeroNode [no=4, name=林冲]
中序遍历
HeroNode [no=2, name=吴用]
HeroNode [no=1, name=宋江]
HeroNode [no=5, name=关胜]
HeroNode [no=3, name=卢俊义]
HeroNode [no=4, name=林冲]
后序遍历
HeroNode [no=2, name=吴用]
HeroNode [no=5, name=关胜]
HeroNode [no=4, name=林冲]
HeroNode [no=3, name=卢俊义]
HeroNode [no=1, name=宋江]# 1.4.4、总结
-
看输出父节点的顺序, 就确定是前序, 中序还是后序
-
前序遍历递归图解
- 中序遍历递归图解
- 后序遍历递归图解
# 1.5、二叉树的查找
# 1.5.1、代码思路
- 将二叉树的前、中、后序遍历改为查找即可
- 编码思路:
- 如果查找到目标节点,直接返回,结束递归
- 如果找不到,继续递归执行前(中、后)序查找
# 1.5.2、前 中 后序查找
- 定义二叉树节点
//先创建 HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; // 默认null
private HeroNode right; // 默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
// 前序遍历查找
public HeroNode preOrderSearch(int no) {
// 比较当前结点是不是
if (this.no == no) {
return this;
}
// 1.则判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
// 2.如果左递归前序查找,找到结点,则返回
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if (resNode != null) {// 说明我们左子树找到
return resNode;
}
// 1.左递归前序查找,找到结点,则返回,否继续判断,
// 2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
// 中序遍历查找
public HeroNode infixOrderSearch(int no) {
// 判断当前结点的左子节点是否为空,如果不为空,则递归中序查找
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
// 如果找到,则返回,如果没有找到,就和当前结点比较,如果是则返回当前结点
if (this.no == no) {
return this;
}
// 否则继续进行右递归的中序查找
if (this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
// 后序遍历查找
public HeroNode postOrderSearch(int no) {
// 判断当前结点的左子节点是否为空,如果不为空,则递归后序查找
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if (resNode != null) {// 说明在左子树找到
return resNode;
}
// 如果左子树没有找到,则向右子树递归进行后序遍历查找
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
// 如果左右子树都没有找到,就比较当前结点是不是
if (this.no == no) {
return this;
}
return resNode;
}
}- 定义二叉树:二叉树需要一个根节点 root 作为整个树的入口
//定义 BinaryTree 二叉树
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
// 删除结点
public void delNode(int no) {
if (root != null) {
// 如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if (root.getNo() == no) {
root = null;
} else {
// 递归删除
root.delNode(no);
}
} else {
System.out.println("空树,不能删除~");
}
}
// 前序遍历查找
public HeroNode preOrderSearch(int no) {
if (root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
// 中序遍历查找
public HeroNode infixOrderSearch(int no) {
if (root != null) {
return root.infixOrderSearch(no);
} else {
return null;
}
}
// 后序遍历查找
public HeroNode postOrderSearch(int no) {
if (root != null) {
return this.root.postOrderSearch(no);
} else {
return null;
}
}
}# 1.5.3、测试代码
- 测试代码:测试前序、中序、后序查找
public static void main(String[] args) {
// 先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
// 创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
// 说明,我们先手动创建该二叉树,后面我们学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
// 前序遍历
System.out.println("前序遍历方式~~~");
HeroNode resNode = binaryTree.preOrderSearch(4);
if (resNode != null) {
System.out.printf("找到了,信息为 no=%d name=%s\n", resNode.getNo(), resNode.getName());
} else {
System.out.printf("没有找到 no = %d 的英雄\n", 4);
}
System.out.println();
// 中序遍历查找
System.out.println("中序遍历方式~~~");
resNode = binaryTree.infixOrderSearch(5);
if (resNode != null) {
System.out.printf("找到了,信息为 no=%d name=%s\n", resNode.getNo(), resNode.getName());
} else {
System.out.printf("没有找到 no = %d 的英雄\n", 5);
}
System.out.println();
// 后序遍历查找
System.out.println("后序遍历方式~~~");
resNode = binaryTree.postOrderSearch(6);
if (resNode != null) {
System.out.printf("找到了,信息为 no=%d name=%s\n", resNode.getNo(), resNode.getName());
} else {
System.out.printf("没有找到 no = %d 的英雄\n", 6);
}
System.out.println();
}- 程序运行结果
前序遍历方式~~~
找到了,信息为 no=4 name=林冲
中序遍历方式~~~
找到了,信息为 no=5 name=关胜
后序遍历方式~~~
没有找到 no = 6 的英雄# 1.6、二叉树的删除
# 1.6.1、二叉树删除的要求
- 如果删除的节点是叶子节点, 则删除该节点
- 如果删除的节点是非叶子节点, 则删除该子树
# 1.6.2、代码思路
- 由于树的本质还是单向链表:
- 单向链表无法实现自删除,我们需要定位至待删除节点的前一个节点,才能执行删除
- 同样,如果我们直接定位至二叉树中待删除的节点,那么其父节点信息便会丢失,所以我们一定要定位至待删除节点的父节点
- 编码思路:
- 先判断根节点 root 是不是待删除的节点,如果是,则删除根节点,否则开始执行递归
- 判断当前节点(this)的左节点是否为待删除的节点,如果是,删除 this.left ,然后返回,结束递归
- 判断当前节点(this)的左节点是否为待删除的节点,如果是,删除 this.right,然后返回,结束递归
- 否则继续执行左递归,左递归执行完后,执行右递归
# 1.6.3、二叉树的递归删除
- 定义二叉树节点
//先创建 HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; // 默认null
private HeroNode right; // 默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
// 递归删除结点
// 1.如果删除的节点是叶子节点,则删除该节点
// 2.如果删除的节点是非叶子节点,则删除该子树
public void delNode(int no) {
// 思路
/*
* 1. 因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除结点,而不能去判断当前这个结点是不是需要删除结点.
* 2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
* 3. 如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
* 4. 如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除 5. 如果第4步也没有删除结点,则应当向右子树进行递归删除.
*
*/
// 2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
if (this.left != null && this.left.no == no) {
this.left = null;
return;
}
// 3.如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
if (this.right != null && this.right.no == no) {
this.right = null;
return;
}
// 4.我们就需要向左子树进行递归删除
if (this.left != null) {
this.left.delNode(no);
}
// 5.则应当向右子树进行递归删除
if (this.right != null) {
this.right.delNode(no);
}
}
}- 定义二叉树:二叉树需要一个根节点 root 作为整个树的入口
//定义 BinaryTree 二叉树
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
// 删除结点
public void delNode(int no) {
if (root != null) {
// 如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if (root.getNo() == no) {
root = null;
} else {
// 递归删除
root.delNode(no);
}
} else {
System.out.println("空树,不能删除~");
}
}
}
# 1.6.4、测试代码
- 代码
public static void main(String[] args) {
// 先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
// 创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
// 说明,我们先手动创建该二叉树,后面我们学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
// 测试一把删除结点
System.out.println("删除前,前序遍历");
binaryTree.preOrder(); // 1,2,3,5,4
System.out.println();
binaryTree.delNode(5);
System.out.println("删除节点 5 后,前序遍历");
binaryTree.preOrder(); // 1,2,3,4
System.out.println();
binaryTree.delNode(3);
System.out.println("删除子树 3 后,前序遍历");
binaryTree.preOrder(); // 1,2
}- 程序运行结果
删除前,前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
HeroNode [no=3, name=卢俊义]
HeroNode [no=5, name=关胜]
HeroNode [no=4, name=林冲]
删除节点 5 后,前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
HeroNode [no=3, name=卢俊义]
HeroNode [no=4, name=林冲]
删除子树 3 后,前序遍历
HeroNode [no=1, name=宋江]
HeroNode [no=2, name=吴用]
# 1.7、二叉树的全部代码
- 叶子节点的定义
//先创建 HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; // 默认null
private HeroNode right; // 默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
// 编写前序遍历的方法
public void preOrder() {
System.out.println(this); // 先输出父结点
// 递归向左子树前序遍历
if (this.left != null) {
this.left.preOrder();
}
// 递归向右子树前序遍历
if (this.right != null) {
this.right.preOrder();
}
}
// 中序遍历
public void infixOrder() {
// 递归向左子树中序遍历
if (this.left != null) {
this.left.infixOrder();
}
// 输出父结点
System.out.println(this);
// 递归向右子树中序遍历
if (this.right != null) {
this.right.infixOrder();
}
}
// 后序遍历
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
// 前序遍历查找
public HeroNode preOrderSearch(int no) {
// 比较当前结点是不是
if (this.no == no) {
return this;
}
// 1.则判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
// 2.如果左递归前序查找,找到结点,则返回
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if (resNode != null) {// 说明我们左子树找到
return resNode;
}
// 1.左递归前序查找,找到结点,则返回,否继续判断,
// 2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
// 中序遍历查找
public HeroNode infixOrderSearch(int no) {
// 判断当前结点的左子节点是否为空,如果不为空,则递归中序查找
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
// 如果找到,则返回,如果没有找到,就和当前结点比较,如果是则返回当前结点
if (this.no == no) {
return this;
}
// 否则继续进行右递归的中序查找
if (this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
// 后序遍历查找
public HeroNode postOrderSearch(int no) {
// 判断当前结点的左子节点是否为空,如果不为空,则递归后序查找
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if (resNode != null) {// 说明在左子树找到
return resNode;
}
// 如果左子树没有找到,则向右子树递归进行后序遍历查找
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
// 如果左右子树都没有找到,就比较当前结点是不是
if (this.no == no) {
return this;
}
return resNode;
}
// 递归删除结点
// 1.如果删除的节点是叶子节点,则删除该节点
// 2.如果删除的节点是非叶子节点,则删除该子树
public void delNode(int no) {
// 思路
/*
* 1. 因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除结点,而不能去判断当前这个结点是不是需要删除结点. 2.
* 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除) 3.
* 如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除) 4.
* 如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除 5. 如果第4步也没有删除结点,则应当向右子树进行递归删除.
*
*/
// 2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
if (this.left != null && this.left.no == no) {
this.left = null;
return;
}
// 3.如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
if (this.right != null && this.right.no == no) {
this.right = null;
return;
}
// 4.我们就需要向左子树进行递归删除
if (this.left != null) {
this.left.delNode(no);
}
// 5.则应当向右子树进行递归删除
if (this.right != null) {
this.right.delNode(no);
}
}
}- 二叉树的定义
//定义 BinaryTree 二叉树
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
// 前序遍历
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
// 中序遍历
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
// 后序遍历
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
// 前序遍历查找
public HeroNode preOrderSearch(int no) {
if (root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
// 中序遍历查找
public HeroNode infixOrderSearch(int no) {
if (root != null) {
return root.infixOrderSearch(no);
} else {
return null;
}
}
// 后序遍历查找
public HeroNode postOrderSearch(int no) {
if (root != null) {
return this.root.postOrderSearch(no);
} else {
return null;
}
}
// 删除结点
public void delNode(int no) {
if (root != null) {
// 如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if (root.getNo() == no) {
root = null;
} else {
// 递归删除
root.delNode(no);
}
} else {
System.out.println("空树,不能删除~");
}
}
}# 1.8、课后练习
- 如果要删除的节点是非叶子节点, 现在我们不希望将该非叶子节点为根节点的子树删除, 需要指定规则,假如规定如下:
- 如果该非叶子节点 A 只有一个子节点 B, 则子节点 B 替代节点 A
- 如果该非叶子节点 A 有左子节点 B 和右子节点 C, 则让左子节点 B 替代节点 A。
- 请大家思考, 如何完成该删除功能,后面在讲解二叉排序树时, 在给大家讲解具体的删除方法
# 2、顺序存储二叉树
# 2.1、顺序存储二叉树的概念
# 2.1.1、顺序存储二叉树与数组的转换
-
基本说明:从数据存储来看,数组存储方式和树的存储方式可以相互转换,即数组可
以转换成树,树也可以转换成数组。
-
要求:
- 右图的二叉树的结点,要求以数组的方式来存放 arr : [1, 2, 3, 4, 5, 6, 6]
- 要求在遍历数组 arr 时,仍然可以用前序遍历,中序遍历和后序遍历的方式完成结点的遍历
# 2.1.2、顺序存储二叉树的特点
-
顺序存储二叉树特点
- 顺序二叉树通常只考虑完全二叉树
- 顺序存储二叉树中第 n 个元素的左子节点对应的数组下标为 2 * n + 1
- 顺序存储二叉树中第 n 个元素的右子节点对应的数组下标为 2 * n + 2
- 顺序存储二叉树中第 n 个元素的父节点对应的数组下标为 (n-1) / 2
- n 的含义: 表示二叉树中的第几个元素(按 0 开始编号,如图所示)
-
下标怎么来的?
-
顺序存储二叉树通常只考虑完全二叉树,完全二叉树的节点个数规律为:1, 2, 4, 8, 12 , … 即 2 的 n 次方
-
每个父节点都会延伸出两个子节点,假设当前节点编号为 n (索引从 0 开始),设当前节点在第 x 层(索引从 1 开始),可得如下数据:
-
1~(x-1) 层所拥有的的节点个数:2n-1 -1
-
1~x 层所拥有的节点个数:2n - 1
-
在第 x 层,节点 n 后面有多少个节点:
back = 2n - 1 - n - 1 = 2n -n - 2
-
在第 x 层,节点 n 前面有多少个节点:
front = n - (2n-1 -1) = n - 2n-1 + 1
-
在第 x+1 层,节点 n 左节点前面有多少个节点:
frontDouble = 2 * (n - 2n-1 + 1) = 2n - 2n + 2
-
所以节点 n 左节点的索引为:
index = n + back + frontDouble + 1 = n + (2n -n - 2) + (2n - 2n + 2) + 1 = 2*n + 1
-
-
# 2.2、顺序存储二叉树的遍历
# 2.2.1、代码思路
- 和之前链表二叉树一样,之前用 left 指针和 right 指针寻找左右子节点,实现递归,只不过顺序存储二叉树使用数组下标寻找左右子节点
- 何时结束递归?当数组下标越界时,说明当前节点已经没有左节点或右节点,已经递归至最深处,此时就应该停止递归,开始回溯
# 2.2.2、前 中 后序遍历
- 编写顺序存储二叉树的前序、中序、后序遍历
//编写一个ArrayBinaryTree, 实现顺序存储二叉树遍历
class ArrBinaryTree {
private int[] arr;// 存储数据结点的数组
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
// 重载preOrder
public void preOrder() {
this.preOrder(0);
}
// 顺序存储二叉树的前序遍历
// index :数组下标
public void preOrder(int index) {
// 如果数组为空,或者 arr.length = 0
if (arr == null || arr.length == 0) {
System.out.println("数组为空,不能执行二叉树的前序遍历");
}
// 输出当前这个元素
System.out.println(arr[index]);
// 向左递归遍历
if ((index * 2 + 1) < arr.length) {
preOrder(2 * index + 1);
}
// 向右递归遍历
if ((index * 2 + 2) < arr.length) {
preOrder(2 * index + 2);
}
}
public void infixOrder() {
this.infixOrder(0);
}
// 顺序存储二叉树的中序遍历
public void infixOrder(int index) {
// 如果数组为空,或者 arr.length = 0
if (arr == null || arr.length == 0) {
System.out.println("数组为空,不能执行二叉树的前序遍历");
}
// 向左递归遍历
if ((index * 2 + 1) < arr.length) {
infixOrder(2 * index + 1);
}
// 输出当前这个元素
System.out.println(arr[index]);
// 向右递归遍历
if ((index * 2 + 2) < arr.length) {
infixOrder(2 * index + 2);
}
}
public void postOrder() {
this.postOrder(0);
}
// 顺序存储二叉树的中序遍历
public void postOrder(int index) {
// 如果数组为空,或者 arr.length = 0
if (arr == null || arr.length == 0) {
System.out.println("数组为空,不能执行二叉树的前序遍历");
}
// 向左递归遍历
if ((index * 2 + 1) < arr.length) {
postOrder(2 * index + 1);
}
// 向右递归遍历
if ((index * 2 + 2) < arr.length) {
postOrder(2 * index + 2);
}
// 输出当前这个元素
System.out.println(arr[index]);
}
}# 2.2.3、测试代码
- 代码
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
// 创建一个 ArrBinaryTree
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
arrBinaryTree.preOrder(); // 1,2,4,5,3,6,7
System.out.println();
arrBinaryTree.infixOrder(); // 4,2,5,1,6,3,7
System.out.println();
arrBinaryTree.postOrder(); // 4,5,2,6,7,3,1
}- 程序运行结果
1
2
4
5
3
6
7
4
2
5
1
6
3
7
4
5
2
6
7
3
1# 2.3、顺序存储二叉树应用实例
- 八大排序算法中的堆排序,就会使用到顺序存储二叉树, 关于堆排序,我们放在【树结构实际应用】章节讲解。
# 3、线索化二叉树
# 3.1、引出问题
-
将数列 {1, 3, 6, 8, 10, 14} 构建成一颗二叉树,当我们对这颗二叉树进行中序遍历时, 输出数列为
-
但是 6, 8, 10, 14 这几个节点的左右指针,并没有完全的利用上,如果我们希望充分的利用 各个节点的左右指针, 让各个节点可以指向自己的前后节点,怎么办?
-
解决方案:线索二叉树
# 3.2、线索二叉树基本介绍
- n 个结点的二叉链表中含有 n+1 【公式 2n-(n-1)=n+1】 个空指针域。 利用二叉链表中的空指针域, 存放指向该结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为 "线索")
- 这种加上了线索的二叉链表称为线索链表, 相应的二叉树称为线索二叉树 (Threaded BinaryTree)。
- 根据线索性质的不同, 线索二叉树可分为前序线索二叉树、 中序线索二叉树和后序线索二叉树三种
- 前驱结点和后继节点:
- 一个结点的前一个结点, 称为前驱结点
- 一个结点的后一个结点, 称为后继结点
- 当我们对二叉树进行中序遍历时, 得到的数列为
- 那么 8 节点的前驱结点为 null ,8 和后驱节点为 3
- 那么 3 节点的前驱结点为 8 ,3 和后驱节点为 10
- 以此类推…
# 3.3、线索二叉树的生成
# 3.3.1、代码思路
-
如何实现线索二叉树?以中序线索化为例,按照上面的步骤操作即可
-
怎么知道当前节点的前驱结点和后继节点?
- 想想单链表的删除是怎么做的?我们记录当前节点的前一个节点,在程序中使用 pre 指针记录当前正在遍历的节点 curNode ,以及其前驱结点 preNode
- 如果条件满足,preNode 就是 curNode 的前驱结点:
curNode.left = pre; - 如果条件满足,curNode 节点就是 preNode 的后继节点:
pre.right = curNode;
-
何时递归完毕?当前递归至最深层,curNode 为空时开始回溯:
curNode == null -
举例说明:
- 我们进行中序遍历时,先执行左递归至最深层
- 对于图例来说,就是递归到节点 8 左节点,满足
node.left == null,开始执行回溯 - 于是我们回到节点 8 ,该节点并没有前驱结点,即前驱结点为 null ,恰好此时 pre 也为 null
- 设置节点 8 的前驱结点:
node.left = pre; - 操作完成后,pre 和 node 指针向后移动一步
- 回溯到节点 3 ,节点 3 的 pre 节点是节点 8
- 设置节点 8 的后继节点:
pre.right = node; - 操作完成后,pre 和 node 指针向后移动一步
- 继续执行右递归,节点 10 的前驱结点为 3
- 设置节点 10 的前驱结点:
node.left = pre; - 操作完成后,pre 和 node 指针向后移动一步
- 以此类推,递归至最后,所有线索都已设置完毕
- 操作完成后,pre 和 node 指针向后移动一步,此时
node == null,递归完毕,节点 6 的 right 指针的类型为真正的子节点,并非
-
大致流程:
- 递归结束条件:
node == null - 执行左递归
- 设置前驱结点、后继节点,并后移 pre 和 node 指针(pre 指针需手动移动,node 指针其实是通过递归来移动的)
- 执行右递归
- 递归结束条件:
- 关于线索化之后的二叉树:只有一个右节点的 right 域为 null ,这个右节点是整棵树最深层的右节点,遍历到该右节点时,表示整棵树遍历完成
# 3.3.2、代码实现
- 由于将原有的指针域(left 和 right 指针)指向了前驱节点和后继节点,所以代码里面需要表示当前指针到底是指向了真正的子节点还是前驱节点或后继节点
- leftType 、rightType:0 表示指向真正的子节点,1 表示指向前驱节点或后继节点
//先创建HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; // 默认null
private HeroNode right; // 默认null
// 说明
// 1. 如果leftType == 0 表示指向的是左子树, 如果 1 则表示指向前驱结点
// 2. 如果rightType == 0 表示指向是右子树, 如果 1表示指向后继结点
private int leftType;
private int rightType;
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
}- 线索二叉树的定义:
//定义ThreadedBinaryTree 实现了线索化功能的二叉树
class ThreadedBinaryTree {
private HeroNode root;
// 为了实现线索化,需要创建一个指向当前结点的前驱结点的指针
// 在递归进行线索化时,pre 总是保留前一个结点
private HeroNode pre = null;
public void setRoot(HeroNode root) {
this.root = root;
}
// 重载一把threadedNodes方法
public void threadedNodes() {
this.threadedNodes(root);
}
// 编写对二叉树进行中序线索化的方法
// node 就是当前需要线索化的结点
public void threadedNodes(HeroNode node) {
// 如果node==null, 不能线索化
if (node == null) {
return;
}
// (一)先线索化左子树
threadedNodes(node.getLeft());
// (二)线索化当前结点[有难度]
// 处理当前结点的前驱结点
// 以8结点来理解
// 8结点的.left = null , 8结点的.leftType = 1
if (node.getLeft() == null) {
// 让当前结点的左指针指向前驱结点
node.setLeft(pre);
// 修改当前结点的左指针的类型,指向前驱结点
node.setLeftType(1);
}
// 处理后继结点
if (pre != null && pre.getRight() == null) {
// 让前驱结点的右指针指向当前结点
pre.setRight(node);
// 修改前驱结点的右指针类型
pre.setRightType(1);
}
// !!! 每处理一个结点后,让当前结点是下一个结点的前驱结点
pre = node;
// (三)在线索化右子树
threadedNodes(node.getRight());
}
}# 3.3.3、测试代码
- 代码
public static void main(String[] args) {
// 测试一把中序线索二叉树的功能
HeroNode root = new HeroNode(1, "tom");
HeroNode node2 = new HeroNode(3, "jack");
HeroNode node3 = new HeroNode(6, "smith");
HeroNode node4 = new HeroNode(8, "mary");
HeroNode node5 = new HeroNode(10, "king");
HeroNode node6 = new HeroNode(14, "dim");
// 二叉树,后面我们要递归创建, 现在简单处理使用手动创建
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node3.setLeft(node6);
// 测试中序线索化
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(root);
threadedBinaryTree.threadedNodes();
// 测试: 以10号节点测试
HeroNode leftNode = node5.getLeft();
HeroNode rightNode = node5.getRight();
System.out.println("10号结点的前驱结点是 =" + leftNode); // 3
System.out.println("10号结点的后继结点是=" + rightNode); // 1
}- 程序运行结果
10号结点的前驱结点是 =HeroNode [no=3, name=jack]
10号结点的后继结点是=HeroNode [no=1, name=tom]# 3.4、线索二叉树的遍历
# 3.4.1、代码思路
-
为什么我们要做线索化?
- 因为线索化后, 各个结点指向有变化, 因此原来的遍历方式不能使用, 这时需要使用新的方式遍历线索化二叉树, 各个节点可以通过线性方式遍历, 因此无需使用递归方式, 这样也提高了遍历的效率。 遍历的次序应当和中序遍历保持一致。
- 以中序遍历为例,线索化可以让每个具有前驱结点的左节点的 right 指针都能指向其下一个要遍历的节点(后继节点)
- 我们先找到第一个具有前驱结点的左节点(整棵树最深层的左叶子节点),我们沿着该左叶子节点的后继节点遍历,可以中序遍历的结果
- 如果遍历到的节点没有后继节点,那么说明该节点 left 和 right 都有节点,直接输出其右节点,并以该右节点根节点,继续执行上一步操作,往最深处寻找第一个具有前驱结点的左节点(当前步骤最深层的左叶子节点),我们继续沿着左叶子节点的后继节点遍历
- 如此往复,直到最后得到的右节点为 null,上面有讲过,线索二叉树有且只有一个为 null 的 right 指针,该值为 null 时代表整棵树的结束
-
举例说明:
- 因为执行的中序遍历:左 --> 中 --> 后,先执行深度搜索,找到第一个有前驱结点的节点,第一次搜索找到节点 8 ,其前驱结点为 null ,从节点 8 的后继节点为节点 3
- 节点 3 并没有后继节点,只有右节点 10 ,我们拿到节点 10
- 寻找节点 10 下第一个具有前驱结点的节点,恰好就是它本身,然后寻找其后继节点
- 以此类推…
-
大致思路:
- 寻找最深层的具有前驱结点的左节点
- 沿着左节点遍历其后继节点
- 如果没有后继节点,则直接输出其右节点,并以该右节点根节点,继续寻找最深层的具有前驱结点的左节点
- 如此往复,直到最后得到的右节点值为 null
# 3.4.2、代码实现
- HeroNode 节点的定义与之前一样
//先创建HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; // 默认null
private HeroNode right; // 默认null
// 说明
// 1. 如果leftType == 0 表示指向的是左子树, 如果 1 则表示指向前驱结点
// 2. 如果rightType == 0 表示指向是右子树, 如果 1表示指向后继结点
private int leftType;
private int rightType;
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
}- 在 ThreadedBinaryTree 类中添加遍历方法
//定义ThreadedBinaryTree 实现了线索化功能的二叉树
class ThreadedBinaryTree {
private HeroNode root;
// 为了实现线索化,需要创建一个指向当前结点的前驱结点的指针
// 在递归进行线索化时,pre 总是保留前一个结点
private HeroNode pre = null;
public void setRoot(HeroNode root) {
this.root = root;
}
// 重载一把threadedNodes方法
public void threadedNodes() {
this.threadedNodes(root);
}
// 编写对二叉树进行中序线索化的方法
// node 就是当前需要线索化的结点
public void threadedNodes(HeroNode node) {
// 如果node==null, 不能线索化
if (node == null) {
return;
}
// (一)先线索化左子树
threadedNodes(node.getLeft());
// (二)线索化当前结点[有难度]
// 处理当前结点的前驱结点
// 以8结点来理解
// 8结点的.left = null , 8结点的.leftType = 1
if (node.getLeft() == null) {
// 让当前结点的左指针指向前驱结点
node.setLeft(pre);
// 修改当前结点的左指针的类型,指向前驱结点
node.setLeftType(1);
}
// 处理后继结点
if (pre != null && pre.getRight() == null) {
// 让前驱结点的右指针指向当前结点
pre.setRight(node);
// 修改前驱结点的右指针类型
pre.setRightType(1);
}
// !!! 每处理一个结点后,让当前结点是下一个结点的前驱结点
pre = node;
// (三)在线索化右子树
threadedNodes(node.getRight());
}
// 遍历线索化二叉树的方法
public void threadedList() {
// 定义一个变量,存储当前遍历的结点,从root开始
HeroNode node = root;
while (node != null) {
// 循环的找到leftType == 1的结点,第一个找到就是8结点
// 后面随着遍历而变化,因为当leftType==1时,说明该结点是按照线索化处理后的有效结点
while (node.getLeftType() == 0) {
node = node.getLeft();
}
// 打印当前这个结点
System.out.println(node);
// 如果当前结点的右指针指向的是后继结点,就一直输出
while (node.getRightType() == 1) {
// 获取到当前结点的后继结点
node = node.getRight();
System.out.println(node);
}
// 替换这个遍历的结点
node = node.getRight();
}
}
}# 3.4.3、测试代码
- 代码
public static void main(String[] args) {
// 测试一把中序线索二叉树的功能
HeroNode root = new HeroNode(1, "tom");
HeroNode node2 = new HeroNode(3, "jack");
HeroNode node3 = new HeroNode(6, "smith");
HeroNode node4 = new HeroNode(8, "mary");
HeroNode node5 = new HeroNode(10, "king");
HeroNode node6 = new HeroNode(14, "dim");
// 二叉树,后面我们要递归创建, 现在简单处理使用手动创建
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node3.setLeft(node6);
// 测试中序线索化
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(root);
threadedBinaryTree.threadedNodes();
// 测试: 以10号节点测试
HeroNode leftNode = node5.getLeft();
HeroNode rightNode = node5.getRight();
System.out.println("10号结点的前驱结点是 =" + leftNode); // 3
System.out.println("10号结点的后继结点是=" + rightNode); // 1
// 当线索化二叉树后,不能再使用原来的遍历方法
System.out.println("使用线索化的方式遍历 线索化二叉树");
threadedBinaryTree.threadedList(); // 8, 3, 10, 1, 14, 6
}- 程序运行结果
使用线索化的方式遍历 线索化二叉树
HeroNode [no=8, name=mary]
HeroNode [no=3, name=jack]
HeroNode [no=10, name=king]
HeroNode [no=1, name=tom]
HeroNode [no=14, name=dim]
HeroNode [no=6, name=smith]# 3.4.4、课后作业
- 这里讲解了中序线索化二叉树,前序线索化二叉树和后序线索化二叉树的分析思路类似, 同学们作为课后作业完成
# 3.5、线索二叉树全部代码
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
// 测试一把中序线索二叉树的功能
HeroNode root = new HeroNode(1, "tom");
HeroNode node2 = new HeroNode(3, "jack");
HeroNode node3 = new HeroNode(6, "smith");
HeroNode node4 = new HeroNode(8, "mary");
HeroNode node5 = new HeroNode(10, "king");
HeroNode node6 = new HeroNode(14, "dim");
// 二叉树,后面我们要递归创建, 现在简单处理使用手动创建
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node3.setLeft(node6);
// 测试中序线索化
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(root);
threadedBinaryTree.threadedNodes();
// 测试: 以10号节点测试
HeroNode leftNode = node5.getLeft();
HeroNode rightNode = node5.getRight();
System.out.println("10号结点的前驱结点是 =" + leftNode); // 3
System.out.println("10号结点的后继结点是=" + rightNode); // 1
// 当线索化二叉树后,不能再使用原来的遍历方法
System.out.println("使用线索化的方式遍历 线索化二叉树");
threadedBinaryTree.threadedList(); // 8, 3, 10, 1, 14, 6
}
}
//定义ThreadedBinaryTree 实现了线索化功能的二叉树
class ThreadedBinaryTree {
private HeroNode root;
// 为了实现线索化,需要创建一个指向当前结点的前驱结点的指针
// 在递归进行线索化时,pre 总是保留前一个结点
private HeroNode pre = null;
public void setRoot(HeroNode root) {
this.root = root;
}
// 重载一把threadedNodes方法
public void threadedNodes() {
this.threadedNodes(root);
}
// 编写对二叉树进行中序线索化的方法
// node 就是当前需要线索化的结点
public void threadedNodes(HeroNode node) {
// 如果node==null, 不能线索化
if (node == null) {
return;
}
// (一)先线索化左子树
threadedNodes(node.getLeft());
// (二)线索化当前结点[有难度]
// 处理当前结点的前驱结点
// 以8结点来理解
// 8结点的.left = null , 8结点的.leftType = 1
if (node.getLeft() == null) {
// 让当前结点的左指针指向前驱结点
node.setLeft(pre);
// 修改当前结点的左指针的类型,指向前驱结点
node.setLeftType(1);
}
// 处理后继结点
if (pre != null && pre.getRight() == null) {
// 让前驱结点的右指针指向当前结点
pre.setRight(node);
// 修改前驱结点的右指针类型
pre.setRightType(1);
}
// !!! 每处理一个结点后,让当前结点是下一个结点的前驱结点
pre = node;
// (三)在线索化右子树
threadedNodes(node.getRight());
}
// 遍历线索化二叉树的方法
public void threadedList() {
// 定义一个变量,存储当前遍历的结点,从root开始
HeroNode node = root;
while (node != null) {
// 循环的找到leftType == 1的结点,第一个找到就是8结点
// 后面随着遍历而变化,因为当leftType==1时,说明该结点是按照线索化处理后的有效结点
while (node.getLeftType() == 0) {
node = node.getLeft();
}
// 打印当前这个结点
System.out.println(node);
// 如果当前结点的右指针指向的是后继结点,就一直输出
while (node.getRightType() == 1) {
// 获取到当前结点的后继结点
node = node.getRight();
System.out.println(node);
}
// 替换这个遍历的结点
node = node.getRight();
}
}
}
//先创建HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; // 默认null
private HeroNode right; // 默认null
// 说明
// 1. 如果leftType == 0 表示指向的是左子树, 如果 1 则表示指向前驱结点
// 2. 如果rightType == 0 表示指向是右子树, 如果 1表示指向后继结点
private int leftType;
private int rightType;
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
}# 树结构实际应用
# 1、堆排序
# 1.1、堆排序基本介绍
- 堆排序是利用堆这种数据结构而设计的一种排序算法, 堆排序是一种选择排序, 它的最坏, 最好, 平均时间复杂度均为 O (nlogn), 它也是不稳定排序。
- 堆是具有以下性质的完全二叉树:
- 每个结点的值都大于或等于其左右孩子结点的值, 称为大顶堆,注意:没有要求结点的左孩子的值和右孩子的值的大小关系。
- 每个结点的值都小于或等于其左右孩子结点的值, 称为小顶堆
- 完全二叉树:一棵深度为 k 的有 n 个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为 i(1≤i≤n)的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树
- 一般升序采用大顶堆, 降序采用小顶堆
- 大顶堆特点:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] ,i 对应第几个节点,i 从 0 开始编号
- 小顶堆特点:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] ,i 对应第几个节点,i 从 0 开始编号
# 1.2、堆排序基本思想
- 将待排序序列构造成一个大顶堆
- 此时, 整个序列的最大值就是堆顶的根节点
- 将其与末尾元素进行交换, 此时末尾就为最大值
- 然后将剩余 n-1 个元素重新构造成一个堆, 这样会得到 n 个元素的次小值。 如此反复执行, 便能得到一个有序序列了
- 可以看到在构建大顶堆的过程中, 元素的个数逐渐减少, 最后就得到一个有序序列了
# 1.3、堆排序步骤图解说明
# 1.3.1、构造大顶堆
- 首先构造初始堆,将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆),假设原始数组为 [4, 6, 8, 5, 9]
- 此时我们从最后一个非叶子结点开始(叶子结点自然不用调整,第一个非叶子结点
arr.length/2-1=5/2-1=1,也就是下面的 6 结点),从左至右,从下至上进行调整。
- 找到第二个非叶节点 4,由于 [4,9,8] 中 9 元素最大,4 和 9 交换
- 这时,交换导致了子根 [4,5,6] 结构混乱,继续调整,[4,5,6] 中 6 最大,交换 4 和 6
# 1.3.2、丢弃堆顶元素
- 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换,步骤如下:
- 将堆顶元素 9 和末尾元素 4 进行交换
# 1.3.3、重操旧业
- 照着之前的方法重新调整结构:将栈顶元素 4 与节点 8 互换,使其继续满足堆定义
- 再将堆顶元素 8 与末尾元素 5 进行交换,得到第二大元素 8
- 后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
# 1.4、堆排序代码思路
# 1.4.1、堆排序基本思路
- 将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
- 将堆顶元素与末尾元素交换,将最大元素 “沉” 到数组末端;
- 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整 + 交换步骤,直到整个序列有序。
# 1.4.2、编码思路
-
先将数组转为大顶堆,怎么转?
- 先来个完全二叉树,节点编号从 0 开始
- 从最深层的非叶子节点开始转换,将最深层的非叶子节点 4 转为大顶堆,即将节点 4 的值与其左右子节点(如果有右节点的话)的值相比较,节点 9 的值大于 节点 4 的值,进行交换,交换后,以节点 4 为根节点的子树就是大顶堆咯
- 再去到倒数第二个非叶子节点,执行上述操作,倒数第二个非叶子节点为节点 3 ,将节点 3 的值与节点 8 的值互换,交换后,以节点 3 为根节点的子树就是大顶堆咯
-
再去到倒数第三个非叶子节点,执行上述操作,倒数第三个非叶子节点为节点 2 ,节点 2 满足大顶堆,无需执行交换
-
再去到倒数第四个非叶子节点,执行上述操作,倒数第四个非叶子节点为节点 2 ,节点 2 满足大顶堆,无需执行交换
-
可以看到,这里出现了特例,由于节点 1 的数值比较小,导致以节点 3 为根节点的子树无法构成大顶堆,也导致了以节点 1 为根节点的子树无法构成大顶堆
-
如何解决这个问题?假设当前非叶子节点为 nonLeafNode ,与其交换值的节点为 exNode ,当每次 nonLeafNode 与 exNode 交换值之后,还要去到以 exNode 为根节点的更深层子树,将 exNode 的子树调整为大顶堆
-
以此类推… ,直至退到整棵树的根节点
-
将整个数组转换为大顶堆之后,将堆顶元素与数组最后一个元素交换位置,这样数组最后一个元素就是整个数组中最大的元素,我们就不用管它了
- 现在我们拿着新的完全二叉树:节点 0 到节点 8 ,将其调整为大顶堆
- 这样来想:节点 1 至 节点 8 已经满足大顶堆的特点了,现在只需要把节点 0 沉下去,把最大的节点浮上来,就又是一棵新的大顶堆啦~~~
- 怎么沉?那不还是之前的步骤嘛,判断当前节点值与其左右子节点值的大小
- 如果无需交换:恭喜,已经是大顶堆了
- 如果需要交换:假设当前非叶子节点为 nonLeafNode ,与其交换值的节点为 exNode ,交换节点的值后,还要去到以 exNode 为根节点的更深层子树,将 exNode 的子树调整为大顶堆
# 1.5、堆排序代码实现
# 1.5.1、理解堆排序
- 逐步分解堆排序
public class HeapSort {
public static void main(String[] args) {
// 要求将数组进行升序排序
int arr[] = {4, 6, 8, 5, 9};
heapSort(arr);
System.out.println("排序后=" + Arrays.toString(arr));
}
// 编写一个堆排序的方法
public static void heapSort(int arr[]) {
int temp = 0;
int length = arr.length;
//分步完成
adjustHeap(arr, 1, length);
System.out.println("第一次" + Arrays.toString(arr)); // 4, 9, 8, 5, 6
adjustHeap(arr, 0, length);
System.out.println("第2次" + Arrays.toString(arr)); // 9,6,8,5,4
temp = arr[length - 1];
arr[length - 1] = arr[0];
arr[0] = temp;
length -= 1;
adjustHeap(arr, 0, length);
System.out.println("第3次" + Arrays.toString(arr)); // 8,6,4,5,9
temp = arr[length - 1];
arr[length - 1] = arr[0];
arr[0] = temp;
length -= 1;
adjustHeap(arr, 0, length);
System.out.println("第4次" + Arrays.toString(arr)); // 6,5,4,8,9
temp = arr[length - 1];
arr[length - 1] = arr[0];
arr[0] = temp;
length -= 1;
adjustHeap(arr, 0, length);
System.out.println("第5次" + Arrays.toString(arr)); // 5,4,6,8,9
temp = arr[length - 1];
arr[length - 1] = arr[0];
arr[0] = temp;
length -= 1;
adjustHeap(arr, 0, length);
System.out.println("第6次" + Arrays.toString(arr)); // 4,5,6,8,9
}
// 将一个数组(二叉树), 调整成一个大顶堆
/**
* 功能: 完成 将 以 i 对应的非叶子结点的树调整成大顶堆 举例 int arr[] = {4, 6, 8, 5, 9}; => i = 1 =>
* adjustHeap => 得到 {4, 9, 8, 5, 6} 如果我们再次调用 adjustHeap 传入的是 i = 0 => 得到 {4, 9,
* 8, 5, 6} => {9,6,8,5, 4}
*
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中索引
* @param length 表示对多少个元素继续调整, length 是在逐渐的减少
*/
public static void adjustHeap(int arr[], int i, int length) {
int temp = arr[i];// 先取出当前元素的值,保存在临时变量
// 开始调整
// 说明
// 1. k = i * 2 + 1 :k 是 i结点的左子结点
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
if (k + 1 < length && arr[k] < arr[k + 1]) { // 说明左子结点的值小于右子结点的值
k++; // k 指向右子结点
}
if (arr[k] > temp) { // 如果子结点大于父结点
arr[i] = arr[k]; // 把较大的值赋给当前结点
i = k; // !!! i 指向 k,将小的值沉下去
} else {
break; // !!! 由于是从最深处往前调整,我能保证下面的子树已经是大顶堆了
}
}
// 当for 循环结束后,我们已经将以i 为父结点的树的最大值,放在了 最顶(局部)
arr[i] = temp;// 将temp值放到调整后的位置
}
}- 程序运行结果
第一次[4, 9, 8, 5, 6]
第2次[9, 6, 8, 5, 4]
第3次[8, 6, 4, 5, 9]
第4次[6, 5, 4, 8, 9]
第5次[5, 4, 6, 8, 9]
第6次[4, 5, 6, 8, 9]
排序后=[4, 5, 6, 8, 9]# 1.5.2、编写堆排序
- 编写堆排序算法
// 编写一个堆排序的方法
public static void heapSort(int arr[]) {
int temp = 0;
// 完成我们最终代码
// 将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjustHeap(arr, i, arr.length);
}
/*
* 2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
* 3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
*/
for (int j = arr.length - 1; j > 0; j--) {
// 交换
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
}
// 将一个数组(二叉树), 调整成一个大顶堆
/**
* 功能: 完成 将 以 i 对应的非叶子结点的树调整成大顶堆 举例 int arr[] = {4, 6, 8, 5, 9}; => i = 1 =>
* adjustHeap => 得到 {4, 9, 8, 5, 6} 如果我们再次调用 adjustHeap 传入的是 i = 0 => 得到 {4, 9,
* 8, 5, 6} => {9,6,8,5, 4}
*
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中索引
* @param length 表示对多少个元素继续调整, length 是在逐渐的减少
*/
public static void adjustHeap(int arr[], int i, int length) {
int temp = arr[i];// 先取出当前元素的值,保存在临时变量
// 开始调整
// 说明
// 1. k = i * 2 + 1 :k 是 i结点的左子结点
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
if (k + 1 < length && arr[k] < arr[k + 1]) { // 说明左子结点的值小于右子结点的值
k++; // k 指向右子结点
}
if (arr[k] > temp) { // 如果子结点大于父结点
arr[i] = arr[k]; // 把较大的值赋给当前结点
i = k; // !!! i 指向 k,将小的值沉下去
} else {
break; // !!! 由于是从最深处往前调整,我能保证下面的子树已经是大顶堆了
}
}
// 当for 循环结束后,我们已经将以i 为父结点的树的最大值,放在了 最顶(局部)
arr[i] = temp;// 将temp值放到调整后的位置
}# 1.5.3、代码测试
- 测试代码
public static void main(String[] args) {
// 要求将数组进行升序排序
int arr[] = {4, 6, 8, 5, 9};
heapSort(arr);
System.out.println("排序后=" + Arrays.toString(arr));
}- 程序运行结果
排序后=[4, 5, 6, 8, 9]# 1.5.4、测试堆排序性能
- 测试代码
public class HeapSort {
public static void main(String[] args) {
// 创建要给80000个的随机的数组
int[] arr = new int[8000000];
for (int i = 0; i < 8000000; i++) {
arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
}
System.out.println("排序前");
Date data1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = simpleDateFormat.format(data1);
System.out.println("排序前的时间是=" + date1Str);
heapSort(arr);
Date data2 = new Date();
String date2Str = simpleDateFormat.format(data2);
System.out.println("排序前的时间是=" + date2Str);
}
// 编写一个堆排序的方法
public static void heapSort(int arr[]) {
int temp = 0;
// 完成我们最终代码
// 将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjustHeap(arr, i, arr.length);
}
/*
* 2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
* 3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
*/
for (int j = arr.length - 1; j > 0; j--) {
// 交换
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
}
// 将一个数组(二叉树), 调整成一个大顶堆
/**
* 功能: 完成 将 以 i 对应的非叶子结点的树调整成大顶堆 举例 int arr[] = {4, 6, 8, 5, 9}; => i = 1 =>
* adjustHeap => 得到 {4, 9, 8, 5, 6} 如果我们再次调用 adjustHeap 传入的是 i = 0 => 得到 {4, 9,
* 8, 5, 6} => {9,6,8,5, 4}
*
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中索引
* @param length 表示对多少个元素继续调整, length 是在逐渐的减少
*/
public static void adjustHeap(int arr[], int i, int length) {
int temp = arr[i];// 先取出当前元素的值,保存在临时变量
// 开始调整
// 说明
// 1. k = i * 2 + 1 :k 是 i结点的左子结点
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
if (k + 1 < length && arr[k] < arr[k + 1]) { // 说明左子结点的值小于右子结点的值
k++; // k 指向右子结点
}
if (arr[k] > temp) { // 如果子结点大于父结点
arr[i] = arr[k]; // 把较大的值赋给当前结点
i = k; // !!! i 指向 k,将小的值沉下去
} else {
break; // !!! 由于是从最深处往前调整,我能保证下面的子树已经是大顶堆了
}
}
// 当for 循环结束后,我们已经将以i 为父结点的树的最大值,放在了 最顶(局部)
arr[i] = temp;// 将temp值放到调整后的位置
}
}- 程序运行结果:牛批,八百万数据 1s 搞定
排序前
排序前的时间是=2020-07-18 17:13:27
排序前的时间是=2020-07-18 17:13:28# 2、赫夫曼树
# 2.1、赫夫曼树基本介绍
- 给定 n 个权值作为 n 个叶子结点,构造一棵二叉树,若该树的带权路径长度 (wpl) 达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树 (Huffman Tree),还有的书翻译为霍夫曼树。
- 赫夫曼树是带权路径长度最短的树,权值较大的结点离根较近
# 2.2、赫夫曼树重要概念
- 路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为 1 ,则从根结点到第 L 层结点的路径长度为 L-1
- 结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积
- 树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为 WPL (weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。WPL 最小的就是赫夫曼树
# 2.3、赫夫曼树创建思路图解
-
创建赫夫曼树的流程
- 核心思想:让权值小的节点远离根节点,让权值大的节点靠近根节点
- 从小到大进行排序,将每一个数据, 每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树(左右节点都为空的二叉树)
- 取出根节点权值最小的两颗二叉树,组成一颗新的二叉树,该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树, 以根节点的权值大小再次排序, 不断重复以上的步骤, 直到数列中, 所有的数据都被处理, 就得到一颗赫夫曼树
-
以数组 {13, 7, 8, 3, 29, 6, 1} 为例,排序后的数组为
- 取出最小的两颗二叉树: 1 和 3 ,组成一棵二叉树,其根节点权值为 1+ 3 = 4 ,将权值为 4 的二叉树放回原数组中,重新进行排序,得到
- 取出最小的两颗二叉树: 4 和 6 ,组成一棵二叉树,其根节点权值为 4+ 6 = 10 ,将权值为 10 的二叉树放回原数组中,重新进行排序,得到
- 继续取出最小的两颗二叉树: 7 和 8,组成一棵二叉树,其根节点权值为 7+ 8= 15,将权值为 15 的二叉树放回原数组中,重新进行排序,得到
- 以此类推,直至最后一个根节点,将得到如下结果:
-
编码思路:
- 将集合中的二叉树排序,从中取两个最权值最低的二叉树组成新的二叉树
- 将新的二叉树放回集合中,再从中取两个最权值最低的二叉树组成新的二叉树
- 如此往复 …
- 何时结束?集合中只剩一个元素时,即为整棵赫夫曼树的根节点
# 2.4、赫夫曼树代码实现
- 树节点的定义
// 创建结点类
// 为了让Node 对象支持排序:Collections集合排序
// 让Node 实现Comparable接口
class Node implements Comparable<Node> {
int value; // 结点权值
Node left; // 指向左子结点
Node right; // 指向右子结点
// 写一个前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
@Override
public int compareTo(Node o) {
// 表示从小到大排序
return this.value - o.value;
}
}- 创建赫夫曼树
// 创建赫夫曼树的方法
/**
*
* @param arr 需要创建成哈夫曼树的数组
* @return 创建好后的赫夫曼树的root结点
*/
public static Node createHuffmanTree(int[] arr) {
// 第一步为了操作方便
// 1. 遍历 arr 数组
// 2. 将arr的每个元素构成成一个Node
// 3. 将Node 放入到ArrayList中
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
// 我们处理的过程是一个循环的过程
while (nodes.size() > 1) {
// 排序 从小到大
Collections.sort(nodes);
// 取出根节点权值最小的两颗二叉树
// (1) 取出权值最小的结点(二叉树)
Node leftNode = nodes.get(0);
// (2) 取出权值第二小的结点(二叉树)
Node rightNode = nodes.get(1);
// (3)构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
// (4)从ArrayList删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
// (5)将parent加入到nodes
nodes.add(parent);
}
// 返回哈夫曼树的root结点
return nodes.get(0);
}- 测试代码
public static void main(String[] args) {
int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
Node root = createHuffmanTree(arr);
preOrder(root);
}
// 编写一个前序遍历的方法
public static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("是空树,不能遍历~~");
}
}- 程序运行结果
Node [value=67]
Node [value=29]
Node [value=38]
Node [value=15]
Node [value=7]
Node [value=8]
Node [value=23]
Node [value=10]
Node [value=4]
Node [value=1]
Node [value=3]
Node [value=6]
Node [value=13]# 2.5、赫夫曼树全部代码
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
Node root = createHuffmanTree(arr);
preOrder(root);
}
// 编写一个前序遍历的方法
public static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("是空树,不能遍历~~");
}
}
// 创建赫夫曼树的方法
/**
*
* @param arr 需要创建成哈夫曼树的数组
* @return 创建好后的赫夫曼树的root结点
*/
public static Node createHuffmanTree(int[] arr) {
// 第一步为了操作方便
// 1. 遍历 arr 数组
// 2. 将arr的每个元素构成成一个Node
// 3. 将Node 放入到ArrayList中
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
// 我们处理的过程是一个循环的过程
while (nodes.size() > 1) {
// 排序 从小到大
Collections.sort(nodes);
// 取出根节点权值最小的两颗二叉树
// (1) 取出权值最小的结点(二叉树)
Node leftNode = nodes.get(0);
// (2) 取出权值第二小的结点(二叉树)
Node rightNode = nodes.get(1);
// (3)构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
// (4)从ArrayList删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
// (5)将parent加入到nodes
nodes.add(parent);
}
// 返回哈夫曼树的root结点
return nodes.get(0);
}
}
// 创建结点类
// 为了让Node 对象支持排序:Collections集合排序
// 让Node 实现Comparable接口
class Node implements Comparable<Node> {
int value; // 结点权值
Node left; // 指向左子结点
Node right; // 指向右子结点
// 写一个前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
@Override
public int compareTo(Node o) {
// 表示从小到大排序
return this.value - o.value;
}
}# 3、赫夫曼编码
# 3.1、赫夫曼编码基本介绍
- 赫夫曼编码也翻译为 哈夫曼编码 (Huffman Coding),又称霍夫曼编码,是一种编码方式,属于一种程序算法
- 赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在 20%~90% 之间
- 赫夫曼码是可变字长编码 (VLC) 的一种。Huffman 于 1952 年提出一种编码方法,称之为最佳编码
# 3.2、定长编码与变长编码
# 3.2.1、定长编码
- 通信领域中信息的处理方式:定长编码,比如我需要发送如下字符串:
i like like like java do you like a java // 共40个字符(包括空格)- 上述字符串对应的 ASCII 码为:
105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106 97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97 118 97 //对应Ascii码01101001 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101010 01100001 01110110 01100001 00100000 01100100 01101111 00100000 01111001 01101111 01110101 00100000 01101100 01101001 01101011 01100101 00100000 01100001 00100000 01101010 01100001 01110110 01100001 //对应的二进制 ・按照二进制来传递信息,总的长度是 359 (包括空格)
# 3.2.2、变长编码
- 通信领域中信息的处理方式:变长编码,比如我需要发送如下字符串:
i like like like java do you like a java // 共40个字符(包括空格)- 统计上述字符串出现的各字符出现的次数
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数- ・按照各个字符出现的次数进行编码,原则是出现次数越多的,则编码越小,比如 空格出现了 9 次, 编码为 0 , 其它依次类推
0= , 1=a, 10=i, 11=e, 100=k, 101=l, 110=o, 111=v, 1000=j, 1001=u, 1010=y, 1011=d- 按照上面给各个字符规定的编码,则我们在传输数据时,编码就是:
10010110100... ・缺点:我怎么解码嘞?我是取 1 、还是取 10 、还是取 100 、还是取 1001?
# 3.3、赫夫曼编码原理剖析
-
通信领域中信息的处理方式:赫夫曼编码
-
字符的编码都不能是其他字符编码的前缀,符合此要求的编码叫做前缀编码, 即不能匹配到重复的编码
-
比如我们处理如下字符串
i like like like java do you like a java // 共40个字符(包括空格)- 统计各字符
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数- 按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值,根据赫夫曼编码表确定具体字符的编码
- 根据赫夫曼树,给各个字符的编码 :向左的路径为 0 ;向右的路径为 1
o: 1000 u: 10010 d: 100110 y: 100111 i: 101
a: 110 k: 1110 e: 1111 j: 0000 v: 0001
l: 001 : 01- 按照上面的赫夫曼编码,我们的 "i like like like java do you like a java" 字符串对应的编码为 (注意这里我们使用的无损压缩)
1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110- 编码后长度为 133 ,原来长度是 359 , 压缩了 (359-133) / 359 = 62.9% ,此编码满足前缀编码,即字符的编码都不能是其他字符编码的前缀,不会造成匹配的多义性
- 想想为啥赫夫曼编码就是前缀比编码?从根节点向左(右)走,只有走到叶子节点才是真正需要编码的字符,看图即可明白~
- 注意,这个赫夫曼树根据排序方法不同,也可能不太一样,这样对应的赫夫曼编码也不完全一样,但是 wpl 是一样的,都是最小的
- 比如:如果我们让每次生成的新的二叉树总是排在权值相同的二叉树的最后一个,则生成的二叉树如下,所以我们生成二叉树时,一定要记录该二叉树对应的赫夫曼编码表~~~
- 为什么会这样捏?权重相同的节点都位于二叉树的同一层,虽然编码具体值会发生变化,但是编码长度不会变化呀
# 3.4、赫夫曼编码思路
- 统计字节数组中各个数据的权重
- 将字节数组按照上面的权重值创建赫夫曼树
- 根据上面创建的赫夫曼树获得每个数值对应的可变长编码值(往左走为 0 ,往右走为 1)
- 以每个数值新的编码重新对字符数组进行编码,即可得到赫夫曼编码后的值
# 3.5、赫夫曼编码算法
# 3.5.1、赫夫曼节点定义
- 每个 data 值对应着一个权重值 weight
//创建Node ,待数据和权值
class Node implements Comparable<Node> {
Byte data; // 存放数据(字符)本身,比如'a' => 97 ' ' => 32
int weight; // 权值, 表示字符出现的次数
Node left;//
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
// 从小到大排序
return this.weight - o.weight;
}
public String toString() {
return "Node [data = " + data + " weight=" + weight + "]";
}
// 前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}# 3.5.2、获取数据权重
- 获取字节数组中每个数值对应的权重值
/**
*
* @param bytes 接收字节数组
* @return 返回的就是 List 形式 [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......],
*/
private static List<Node> getNodes(byte[] bytes) {
// 1创建一个ArrayList
ArrayList<Node> nodes = new ArrayList<Node>();
// 遍历 bytes , 统计 每一个byte出现的次数->map[key,value]
Map<Byte, Integer> counts = new HashMap<>();
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) { // Map还没有这个字符数据,第一次
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
// 把每一个键值对转成一个Node 对象,并加入到nodes集合
// 遍历map
for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}# 3.5.3、创建赫夫曼树
- 统计字节数组中每个数值出现的次数,即每个数值对应的权重值,并根据数值及其权重值,来创建赫夫曼树
// 可以通过List 创建对应的赫夫曼树
private static Node createHuffmanTree(List<Node> nodes) {
while (nodes.size() > 1) {
// 排序, 从小到大
Collections.sort(nodes);
// 取出第一颗最小的二叉树
Node leftNode = nodes.get(0);
// 取出第二颗最小的二叉树
Node rightNode = nodes.get(1);
// 创建一颗新的二叉树,它的根节点 没有data, 只有权值
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
// 将已经处理的两颗二叉树从nodes删除
nodes.remove(leftNode);
nodes.remove(rightNode);
// 将新的二叉树,加入到nodes
nodes.add(parent);
}
// nodes 最后的结点,就是赫夫曼树的根结点
return nodes.get(0);
}# 3.5.4、生成赫夫曼编码表
- 根据上面生成的赫夫曼树,获取字节数组中每个数值对应的可变长编码
// 生成赫夫曼树对应的赫夫曼编码
// 思路:将赫夫曼编码表存放在 Map<Byte,String> 形式
// 生成的赫夫曼编码表{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
static Map<Byte, String> huffmanCodes = new HashMap<Byte, String>();
// 为了调用方便,我们重载 getCodes
private static Map<Byte, String> getCodes(Node root) {
if (root == null) {
return null;
}
// 处理root的左子树
getCodes(root.left, "0", new StringBuilder());
// 处理root的右子树
getCodes(root.right, "1", new StringBuilder());
return huffmanCodes;
}
/**
* 功能:将传入的node结点的所有叶子结点的赫夫曼编码得到,并放入到huffmanCodes集合
* @param node 传入结点
* @param code 路径: 左子结点是 0, 右子结点 1
* @param stringBuilder 用于拼接路径
*/
private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
// 因为对象传递的是引用,所以不能再原有的 StringBuilder 上进行操作
StringBuilder curNodeCode = new StringBuilder(stringBuilder);
// 将code 加入到 curNodeCode
curNodeCode.append(code);
if (node != null) { // 如果node == null不处理
// 判断当前node 是叶子结点还是非叶子结点
if (node.data == null) { // 非叶子结点
// 递归处理
// 向左递归
getCodes(node.left, "0", curNodeCode);
// 向右递归
getCodes(node.right, "1", curNodeCode);
} else { // 说明是一个叶子结点
// 就表示找到某个叶子结点的最后
huffmanCodes.put(node.data, curNodeCode.toString());
}
}
}# 3.5.5、生成赫夫曼编码
- 根据原字节数组及其对应的赫夫曼编码表,生成赫夫曼编码,我觉着老师的编码方式有问题,关键就在于最后一个字节,最后一个字节很有可能不满 8 个 bit
- 要么在前面填充 0 ,要么在后面填充 0 ,然后二进制字符串转换为 byte ,想想:
- 如果在前面填充 0 ,解码的时候,你怎么知道前面的 0 ,从哪个 0 开始算起才是有效的 0 ???就比如说最后一个字节编码为 01100 ,好,我们就在前面全填充 0 ,即最后一个字节为 0001100 ,来,你解码的时候,给我把它解出来,是 0001100 、还是 001100、 还是 01100 、还是 1100 ?根本无从下手。。。
- 如果在后面填充 0 ,解码的时候,你怎么知道后面的 0 ,从哪个 0 开始算起才是有效的 0 ???就比如说最后一个字节编码为 01100 ,好,我们就在后面全填充 0 ,即最后一个字节为 00110000 ,来,你解码的时候,给我把它解出来,是 0011 、还是 00110、 还是 001100 、还是 0011000 、还是 00110000 ?根本无从下手。。。
- 所以在赫夫曼编码生成的字节数组最后额外开辟了一个空间,用来存储最后一个字节的有效位数,这样就没得问题啦~~~
//编写一个方法,将字符串对应的byte[] 数组,通过生成的赫夫曼编码表,返回一个赫夫曼编码 压缩后的byte[]
/**
*
* @param bytes 这是原始的字符串对应的 byte[]
* @param huffmanCodes 生成的赫夫曼编码map
* @return 返回赫夫曼编码处理后的 byte[]
*
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
// 1.利用 huffmanCodes 将 bytes 转成 赫夫曼编码对应的字符串
StringBuilder stringBuilder = new StringBuilder();
// 遍历bytes 数组
for (byte b : bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
// 统计返回 byte[] huffmanCodeBytes 长度
// 一句话 int len = (stringBuilder.length() + 7) / 8;
int len;
byte countToEight = (byte) (stringBuilder.length() % 8);
if (countToEight == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
// 后面补零
for (int i = countToEight; i < 8; i++) {
stringBuilder.append('0');
}
}
// 创建 存储压缩后的 byte数组,huffmanCodeBytes[len]记录赫夫曼编码最后一个字节的有效位数
byte[] huffmanCodeBytes = new byte[len + 1];
huffmanCodeBytes[len] = countToEight;
int index = 0;// 记录是第几个byte
for (int i = 0; i < stringBuilder.length(); i += 8) { // 因为是每8位对应一个byte,所以步长 +8
String strByte;
strByte = stringBuilder.substring(i, i + 8);
// 将strByte 转成一个byte,放入到 huffmanCodeBytes
huffmanCodeBytes[index] = (byte) Integer.parseInt(strByte, 2);
index++;
}
return huffmanCodeBytes;
}# 3.5.6、代码测试
- 代码
public static void main(String[] args) {
//如何将 数据进行解压(解码)
//分步过程
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
List<Node> nodes = getNodes(contentBytes);
System.out.println("nodes=" + nodes);
//测试一把,创建的赫夫曼树
System.out.println("生成赫夫曼树");
Node huffmanTreeRoot = createHuffmanTree(nodes);
System.out.println("前序遍历");
huffmanTreeRoot.preOrder();
//测试一把是否生成了对应的赫夫曼编码
Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
System.out.println("~生成的赫夫曼编码表= " + huffmanCodes);
//测试
byte[] huffmanCodeBytes = zip(contentBytes, huffmanCodes);
System.out.println("huffmanCodeBytes=" + Arrays.toString(huffmanCodeBytes));//17
//发送huffmanCodeBytes 数组
}- 程序运行结果
nodes=[Node [data = 32 weight=9], Node [data = 97 weight=5], Node [data = 100 weight=1], Node [data = 101 weight=4], Node [data = 117 weight=1], Node [data = 118 weight=2], Node [data = 105 weight=5], Node [data = 121 weight=1], Node [data = 106 weight=2], Node [data = 107 weight=4], Node [data = 108 weight=4], Node [data = 111 weight=2]]
生成赫夫曼树
前序遍历
Node [data = null weight=40]
Node [data = null weight=17]
Node [data = null weight=8]
Node [data = 108 weight=4]
Node [data = null weight=4]
Node [data = 106 weight=2]
Node [data = 111 weight=2]
Node [data = 32 weight=9]
Node [data = null weight=23]
Node [data = null weight=10]
Node [data = 97 weight=5]
Node [data = 105 weight=5]
Node [data = null weight=13]
Node [data = null weight=5]
Node [data = null weight=2]
Node [data = 100 weight=1]
Node [data = 117 weight=1]
Node [data = null weight=3]
Node [data = 121 weight=1]
Node [data = 118 weight=2]
Node [data = null weight=8]
Node [data = 101 weight=4]
Node [data = 107 weight=4]
~生成的赫夫曼编码表= {32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
huffmanCodeBytes=[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, -32, 5]# 3.5.7、封装赫夫曼编码函数
- 将上述操作封装成一个函数,对外暴露该方法即可
// 使用一个方法,将前面的方法封装起来,便于我们的调用.
/**
*
* @param bytes 原始的字符串对应的字节数组
* @return 是经过 赫夫曼编码处理后的字节数组(压缩后的数组)
*/
private static byte[] huffmanZip(byte[] bytes) {
List<Node> nodes = getNodes(bytes);
// 根据 nodes 创建的赫夫曼树
Node huffmanTreeRoot = createHuffmanTree(nodes);
// 对应的赫夫曼编码(根据 赫夫曼树)
Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
// 根据生成的赫夫曼编码,压缩得到压缩后的赫夫曼编码字节数组
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
return huffmanCodeBytes;
}# 3.6、赫夫曼解码
# 3.6.1、字节转二进制字符串
# 1、字节转二进制字符串方法
- 编写将字节转换为二进制字符串的方法
- 正数:高位补 0 即可,然后截取低八位即可;
- 负数直接截取低八位即可,其实往第八位(索引从 0 开始)补个 1 也没事儿。。。8 位的负数转为 32 位的负数,其 8~31 位都是 1
// 将 byte 转换为对应的字符串
private static String byteToBitString(byte b) {
// 使用变量保存 b
int temp = b; // 将 b 转成 int
temp |= 0x100; // 如果是正数我们需要将高位补零
// 转换为二进制字符串,正数:高位补 0 即可,然后截取低八位即可;负数直接截取低八位即可
// 负数在计算机内存储的是补码,补码转原码:先 -1 ,再取反
String binaryStr = Integer.toBinaryString(temp);
return binaryStr.substring(binaryStr.length() - 8);
}# 2、关于二进制的理解
- 测试代码 1:
public static void main(String[] args) {
byte b = (byte) Integer.parseInt("11110000", 2);
System.out.println(b);
String byteToBitString = byteToBitString(b);
System.out.println(byteToBitString);
}
// 将 byte 转换为对应的字符串
private static String byteToBitString(byte b) {
// 使用变量保存 b
int temp = b; // 将 b 转成 int
temp |= 0x100; // 如果是正数我们需要将高位补零
// 转换为二进制字符串,正数:高位补 0 即可,然后截取低八位即可;负数直接截取低八位即可
// 负数在计算机内存储的是补码,补码转原码:先 -1 ,再取反
String binaryStr = Integer.toBinaryString(temp);
return binaryStr.substring(binaryStr.length() - 8);
}- 程序运行结果
-16
11110000- 测试代码 2:
@SuppressWarnings("unused")
public static void main(String[] args) {
byte b = (byte) Integer.parseInt("01110000", 2);
System.out.println(b);
String byteToBitString = byteToBitString(b);
System.out.println(byteToBitString);
}
// 将 byte 转换为对应的字符串
private static String byteToBitString(byte b) {
// 使用变量保存 b
int temp = b; // 将 b 转成 int
temp |= 0x100; // 如果是正数我们需要将高位补零
// 转换为二进制字符串,正数:高位补 0 即可,然后截取低八位即可;负数直接截取低八位即可
// 负数在计算机内存储的是补码,补码转原码:先 -1 ,再取反
String binaryStr = Integer.toBinaryString(temp);
return binaryStr.substring(binaryStr.length() - 8);
}- 程序运行结果
112
01110000-
关于字节转二进制字符串的总结:
-
为什么要在正数的第八位(索引从 0 开始)补个 1 ,就能实现高位补零的效果?
- 因为如果不补零,调用 Integer.toBinaryString (temp); 方法,只会从第一个非零元素开始输出,会将高位的 0 抹去
- 8 位的正数转为 32 位正数,其 8~31 2 位都是零 ,在其的第八位补个 1 ,就能输出 0~7 位的零呀~~~
-
为什么负数的第八位(索引从 0 开始)补个 1 ,无关紧要?
- 首先搞清楚,负数在计算机中是以补码形式存储,何为补码:原码取反码 + 1
- 分析分析:
- -16 的原码(8 位):1001 0000
- -16 的反码(8 位):1110 1111
- -16 的补码(8 位):1111 0000
- -16 的原码(32 位):1000 0000 0000 0000 0000 0000 0001 0000
- -16 的反码(32 位):1111 1111 1111 1111 1111 1111 1110 1111
- -16 的补码(32 位):1111 1111 1111 1111 1111 1111 1111 0000
- 结论:8 位的负数转为 32 位负数,其 8~31 位都是 1 ,在其的第八位补个 1 ,无关紧要呀~~~
-
# 3.6.2、编写赫夫曼解码
- 编码思路
- 首先根据赫夫曼编码得到的字符数组,反解出赫夫曼编码对应的字符串 huffmanStr
- 因为现在要拿着赫夫曼编码值去找恢复对应的数值,所以我们需要拿到各个编码对应着哪个数值(将赫夫曼码表反转一下就行)
- 在 huffmanStr 中匹配编码值,逐个恢复数据,处理完毕后,便解码得到了原字节数组
- 注意:我这里做了调整,huffmanBytes 中最后一个字节记录了 huffmanBytes 倒数第二个字节的有效位数(从高位开始的有效位数)
// 编写一个方法,完成对压缩数据的解码
/**
*
* @param huffmanCodes 赫夫曼编码表 map
* @param huffmanBytes 赫夫曼编码得到的字节数组
* @return 就是原来的字符串对应的数组
*/
private static byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes) {
// 1. 先得到 huffmanBytes 对应的 二进制的字符串 , 形式 1010100010111...
StringBuilder stringBuilder = new StringBuilder();
// 将byte数组转成二进制的字符串
for (int i = 0; i < huffmanBytes.length - 1; i++) {
byte b = huffmanBytes[i];
String strToAppend = byteToBitString(b);
// 判断是不是最后一个字节
boolean isLastByte = (i == huffmanBytes.length - 2);
if (isLastByte) {
// 得到最后一个字节的有效位数
byte validBits = huffmanBytes[huffmanBytes.length - 1];
strToAppend = strToAppend.substring(0, validBits);
}
stringBuilder.append(strToAppend);
}
// 把字符串按照指定的赫夫曼编码进行解码
// 把赫夫曼编码表进行调换,因为反向查询 a->100 100->a
Map<String, Byte> map = new HashMap<String, Byte>();
for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
// 创建要给集合,存放byte
List<Byte> list = new ArrayList<>();
// i 可以理解成就是索引,扫描 stringBuilder
for (int i = 0; i < stringBuilder.length();) {
int count = 1; // 小的计数器
boolean flag = true;
Byte b = null;
while (flag) {
// 1010100010111...
// 递增的取出 key 1
String key = stringBuilder.substring(i, i + count);// i 不动,让count移动,指定匹配到一个字符
b = map.get(key);
if (b == null) {// 说明没有匹配到
count++;
} else {
// 匹配到
flag = false;
}
}
list.add(b);
i += count;// i 直接移动到 count
}
// 当for循环结束后,我们list中就存放了所有的字符 "i like like like java do you like a java"
// 把list 中的数据放入到byte[] 并返回
byte b[] = new byte[list.size()];
for (int i = 0; i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}# 3.6.3、代码测试
- 代码
public static void main(String[] args) {
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
System.out.println("原来的字符串=" + content);
byte[] huffmanCodesBytes = huffmanZip(contentBytes);
byte[] sourceBytes = decode(huffmanCodes, huffmanCodesBytes);
System.out.println("解码后的字符串=" + new String(sourceBytes)); // "i like like like java do you like a java"
}- 程序运行结果
原来的字符串=i like like like java do you like a java
解码后的字符串=i like like like java do you like a java# 3.7、文件压缩与解压
# 3.7.1、文件压缩
- 将赫夫曼编码得到的字节数组、赫夫曼编码表都要写入到文件中(使用 ObjectOutputStream 流包装 FileOutputStream 流,可直接写入对象)
// 编写方法,将一个文件进行压缩
/**
*
* @param srcFile 你传入的希望压缩的文件的全路径
* @param dstFile 我们压缩后将压缩文件放到哪个目录
*/
public static void zipFile(String srcFile, String dstFile) {
// 创建输出流
OutputStream os = null;
ObjectOutputStream oos = null;
// 创建文件的输入流
FileInputStream is = null;
try {
// 创建文件的输入流
is = new FileInputStream(srcFile);
// 创建一个和源文件大小一样的byte[]
byte[] b = new byte[is.available()];
// 读取文件
is.read(b);
// 直接对源文件压缩
byte[] huffmanBytes = huffmanZip(b);
// 创建文件的输出流, 存放压缩文件
os = new FileOutputStream(dstFile);
// 创建一个和文件输出流关联的ObjectOutputStream
oos = new ObjectOutputStream(os);
// 把 赫夫曼编码后的字节数组写入压缩文件
oos.writeObject(huffmanBytes); // 我们是把
// 这里我们以对象流的方式写入 赫夫曼编码,是为了以后我们恢复源文件时使用
// 注意一定要把赫夫曼编码 写入压缩文件
oos.writeObject(huffmanCodes);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
} finally {
try {
is.close();
oos.close();
os.close();
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
}
}# 3.7.2、文件解压
- 先要得到编码后的字节数组和赫夫曼编码表(使用 ObjectInputStream 流封装 FileInputStream 流 可直接读取对象)
- 再调用赫夫曼解码方法,进行解码
// 编写一个方法,完成对压缩文件的解压
/**
*
* @param zipFile 准备解压的文件
* @param dstFile 将文件解压到哪个路径
*/
public static void unZipFile(String zipFile, String dstFile) {
// 定义文件输入流
InputStream is = null;
// 定义一个对象输入流
ObjectInputStream ois = null;
// 定义文件的输出流
OutputStream os = null;
try {
// 创建文件输入流
is = new FileInputStream(zipFile);
// 创建一个和 is关联的对象输入流
ois = new ObjectInputStream(is);
// 读取byte数组 huffmanBytes
byte[] huffmanBytes = (byte[]) ois.readObject();
// 读取赫夫曼编码表
Map<Byte, String> huffmanCodes = (Map<Byte, String>) ois.readObject();
// 解码
byte[] bytes = decode(huffmanCodes, huffmanBytes);
// 将bytes 数组写入到目标文件
os = new FileOutputStream(dstFile);
// 写数据到 dstFile 文件
os.write(bytes);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
} finally {
try {
os.close();
ois.close();
is.close();
} catch (Exception e2) {
// TODO: handle exception
System.out.println(e2.getMessage());
}
}
}# 3.7.3、代码测试
- 压缩与解压缩
public class HuffmanCode {
public static void main(String[] args) {
// 测试压缩文件
String srcFile = "C:\\Users\\Heygo\\Desktop\\src.png";
String dstFile = "C:\\Users\\Heygo\\Desktop\\src.zip";
zipFile(srcFile, dstFile);
System.out.println("压缩文件ok~~");
// 测试解压文件
srcFile = "C:\\\\Users\\\\Heygo\\\\Desktop\\\\src.zip";
dstFile = "C:\\\\Users\\\\Heygo\\\\Desktop\\\\srcCopy.png";
unZipFile(srcFile, dstFile);
System.out.println("解压成功!");
}- 莫得问题啊
# 3.8、赫夫曼编解码全部代码
public class HuffmanCode {
public static void main(String[] args) {
// 测试压缩文件
String srcFile = "C:\\Users\\Heygo\\Desktop\\src.png";
String dstFile = "C:\\Users\\Heygo\\Desktop\\src.zip";
zipFile(srcFile, dstFile);
System.out.println("压缩文件ok~~");
// 测试解压文件
srcFile = "C:\\\\Users\\\\Heygo\\\\Desktop\\\\src.zip";
dstFile = "C:\\\\Users\\\\Heygo\\\\Desktop\\\\srcCopy.png";
unZipFile(srcFile, dstFile);
System.out.println("解压成功!");
}
/**
*
* @param bytes 接收字节数组
* @return 返回的就是 List 形式 [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......],
*/
private static List<Node> getNodes(byte[] bytes) {
// 1创建一个ArrayList
ArrayList<Node> nodes = new ArrayList<Node>();
// 遍历 bytes , 统计 每一个byte出现的次数->map[key,value]
Map<Byte, Integer> counts = new HashMap<>();
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) { // Map还没有这个字符数据,第一次
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
// 把每一个键值对转成一个Node 对象,并加入到nodes集合
// 遍历map
for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
// 可以通过List 创建对应的赫夫曼树
private static Node createHuffmanTree(List<Node> nodes) {
while (nodes.size() > 1) {
// 排序, 从小到大
Collections.sort(nodes);
// 取出第一颗最小的二叉树
Node leftNode = nodes.get(0);
// 取出第二颗最小的二叉树
Node rightNode = nodes.get(1);
// 创建一颗新的二叉树,它的根节点 没有data, 只有权值
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
// 将已经处理的两颗二叉树从nodes删除
nodes.remove(leftNode);
nodes.remove(rightNode);
// 将新的二叉树,加入到nodes
nodes.add(parent);
}
// nodes 最后的结点,就是赫夫曼树的根结点
return nodes.get(0);
}
// 生成赫夫曼树对应的赫夫曼编码
// 思路:将赫夫曼编码表存放在 Map<Byte,String> 形式
// 生成的赫夫曼编码表{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101,
// 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
static Map<Byte, String> huffmanCodes = new HashMap<Byte, String>();
// 为了调用方便,我们重载 getCodes
private static Map<Byte, String> getCodes(Node root) {
if (root == null) {
return null;
}
// 处理root的左子树
getCodes(root.left, "0", new StringBuilder());
// 处理root的右子树
getCodes(root.right, "1", new StringBuilder());
return huffmanCodes;
}
/**
* 功能:将传入的node结点的所有叶子结点的赫夫曼编码得到,并放入到huffmanCodes集合
* @param node 传入结点
* @param code 路径: 左子结点是 0, 右子结点 1
* @param stringBuilder 用于拼接路径
*/
private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
StringBuilder curNodeCode = new StringBuilder(stringBuilder);
// 将code 加入到 curNodeCode
curNodeCode.append(code);
if (node != null) { // 如果node == null不处理
// 判断当前node 是叶子结点还是非叶子结点
if (node.data == null) { // 非叶子结点
// 递归处理
// 向左递归
getCodes(node.left, "0", curNodeCode);
// 向右递归
getCodes(node.right, "1", curNodeCode);
} else { // 说明是一个叶子结点
// 就表示找到某个叶子结点的最后
huffmanCodes.put(node.data, curNodeCode.toString());
}
}
}
//编写一个方法,将字符串对应的byte[] 数组,通过生成的赫夫曼编码表,返回一个赫夫曼编码 压缩后的byte[]
/**
*
* @param bytes 这是原始的字符串对应的 byte[]
* @param huffmanCodes 生成的赫夫曼编码map
* @return 返回赫夫曼编码处理后的 byte[]
*
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
// 1.利用 huffmanCodes 将 bytes 转成 赫夫曼编码对应的字符串
StringBuilder stringBuilder = new StringBuilder();
// 遍历bytes 数组
for (byte b : bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
// 统计返回 byte[] huffmanCodeBytes 长度
// 一句话 int len = (stringBuilder.length() + 7) / 8;
int len;
byte countToEight = (byte) (stringBuilder.length() % 8);
if (countToEight == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
// 后面补零
for (int i = countToEight; i < 8; i++) {
stringBuilder.append('0');
}
}
// 创建 存储压缩后的 byte数组,huffmanCodeBytes[len]记录赫夫曼编码最后一个字节的有效位数
byte[] huffmanCodeBytes = new byte[len + 1];
huffmanCodeBytes[len] = countToEight;
int index = 0;// 记录是第几个byte
for (int i = 0; i < stringBuilder.length(); i += 8) { // 因为是每8位对应一个byte,所以步长 +8
String strByte;
strByte = stringBuilder.substring(i, i + 8);
// 将strByte 转成一个byte,放入到 huffmanCodeBytes
huffmanCodeBytes[index] = (byte) Integer.parseInt(strByte, 2);
index++;
}
return huffmanCodeBytes;
}
// 使用一个方法,将前面的方法封装起来,便于我们的调用.
/**
*
* @param bytes 原始的字符串对应的字节数组
* @return 是经过 赫夫曼编码处理后的字节数组(压缩后的数组)
*/
private static byte[] huffmanZip(byte[] bytes) {
List<Node> nodes = getNodes(bytes);
// 根据 nodes 创建的赫夫曼树
Node huffmanTreeRoot = createHuffmanTree(nodes);
// 对应的赫夫曼编码(根据 赫夫曼树)
Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
// 根据生成的赫夫曼编码,压缩得到压缩后的赫夫曼编码字节数组
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
return huffmanCodeBytes;
}
// 将 byte 转换为对应的字符串
private static String byteToBitString(byte b) {
// 使用变量保存 b
int temp = b; // 将 b 转成 int
temp |= 0x100; // 如果是正数我们需要将高位补零
// 转换为二进制字符串,正数:高位补 0 即可,然后截取低八位即可;负数直接截取低八位即可
// 负数在计算机内存储的是补码,补码转原码:先 -1 ,再取反
String binaryStr = Integer.toBinaryString(temp);
return binaryStr.substring(binaryStr.length() - 8);
}
// 编写一个方法,完成对压缩数据的解码
/**
*
* @param huffmanCodes 赫夫曼编码表 map
* @param huffmanBytes 赫夫曼编码得到的字节数组
* @return 就是原来的字符串对应的数组
*/
private static byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes) {
// 1. 先得到 huffmanBytes 对应的 二进制的字符串 , 形式 1010100010111...
StringBuilder stringBuilder = new StringBuilder();
// 将byte数组转成二进制的字符串
for (int i = 0; i < huffmanBytes.length - 1; i++) {
byte b = huffmanBytes[i];
String strToAppend = byteToBitString(b);
// 判断是不是最后一个字节
boolean isLastByte = (i == huffmanBytes.length - 2);
if (isLastByte) {
// 得到最后一个字节的有效位数
byte validBits = huffmanBytes[huffmanBytes.length - 1];
strToAppend = strToAppend.substring(0, validBits);
}
stringBuilder.append(strToAppend);
}
// 把字符串按照指定的赫夫曼编码进行解码
// 把赫夫曼编码表进行调换,因为反向查询 a->100 100->a
Map<String, Byte> map = new HashMap<String, Byte>();
for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
// 创建要给集合,存放byte
List<Byte> list = new ArrayList<>();
// i 可以理解成就是索引,扫描 stringBuilder
for (int i = 0; i < stringBuilder.length();) {
int count = 1; // 小的计数器
boolean flag = true;
Byte b = null;
while (flag) {
// 1010100010111...
// 递增的取出 key 1
String key = stringBuilder.substring(i, i + count);// i 不动,让count移动,指定匹配到一个字符
b = map.get(key);
if (b == null) {// 说明没有匹配到
count++;
} else {
// 匹配到
flag = false;
}
}
list.add(b);
i += count;// i 直接移动到 count
}
// 当for循环结束后,我们list中就存放了所有的字符 "i like like like java do you like a java"
// 把list 中的数据放入到byte[] 并返回
byte b[] = new byte[list.size()];
for (int i = 0; i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
// 编写方法,将一个文件进行压缩
/**
*
* @param srcFile 你传入的希望压缩的文件的全路径
* @param dstFile 我们压缩后将压缩文件放到哪个目录
*/
public static void zipFile(String srcFile, String dstFile) {
// 创建输出流
OutputStream os = null;
ObjectOutputStream oos = null;
// 创建文件的输入流
FileInputStream is = null;
try {
// 创建文件的输入流
is = new FileInputStream(srcFile);
// 创建一个和源文件大小一样的byte[]
byte[] b = new byte[is.available()];
// 读取文件
is.read(b);
// 直接对源文件压缩
byte[] huffmanBytes = huffmanZip(b);
// 创建文件的输出流, 存放压缩文件
os = new FileOutputStream(dstFile);
// 创建一个和文件输出流关联的ObjectOutputStream
oos = new ObjectOutputStream(os);
// 把 赫夫曼编码后的字节数组写入压缩文件
oos.writeObject(huffmanBytes); // 我们是把
// 这里我们以对象流的方式写入 赫夫曼编码,是为了以后我们恢复源文件时使用
// 注意一定要把赫夫曼编码 写入压缩文件
oos.writeObject(huffmanCodes);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
} finally {
try {
is.close();
oos.close();
os.close();
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
}
}
// 编写一个方法,完成对压缩文件的解压
/**
*
* @param zipFile 准备解压的文件
* @param dstFile 将文件解压到哪个路径
*/
public static void unZipFile(String zipFile, String dstFile) {
// 定义文件输入流
InputStream is = null;
// 定义一个对象输入流
ObjectInputStream ois = null;
// 定义文件的输出流
OutputStream os = null;
try {
// 创建文件输入流
is = new FileInputStream(zipFile);
// 创建一个和 is关联的对象输入流
ois = new ObjectInputStream(is);
// 读取byte数组 huffmanBytes
byte[] huffmanBytes = (byte[]) ois.readObject();
// 读取赫夫曼编码表
Map<Byte, String> huffmanCodes = (Map<Byte, String>) ois.readObject();
// 解码
byte[] bytes = decode(huffmanCodes, huffmanBytes);
// 将bytes 数组写入到目标文件
os = new FileOutputStream(dstFile);
// 写数据到 dstFile 文件
os.write(bytes);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
} finally {
try {
os.close();
ois.close();
is.close();
} catch (Exception e2) {
// TODO: handle exception
System.out.println(e2.getMessage());
}
}
}
}
//创建Node ,待数据和权值
class Node implements Comparable<Node> {
Byte data; // 存放数据(字符)本身,比如'a' => 97 ' ' => 32
int weight; // 权值, 表示字符出现的次数
Node left;//
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
// 从小到大排序
return this.weight - o.weight;
}
public String toString() {
return "Node [data = " + data + " weight=" + weight + "]";
}
// 前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}# 3.9、赫夫曼编解码总结
- 如果文件本身就是经过压缩处理的,那么使用赫夫曼编码再压缩效率不会有明显变化,比如视频,ppt 等等文件
- 赫夫曼编码是按字节来处理的,因此可以处理所有的文件 (二进制文件、文本文件)
- 如果一个文件中的内容,重复的数据不多,压缩效果也不会很明显
# 4、二叉排序树
# 4.1、二叉排序树需求
# 4.1.1、需求分析
- 给你一个数列 {7, 3, 10, 12, 5, 1, 9} ,要求能够高效的完成对数据的查询和添加。
# 4.1.2、解决方案
- 使用数组
- 数组未排序, 优点:直接在数组尾添加,速度快。 缺点:查找速度慢
- 数组排序,优点:可以使用二分查找,查找速度快,缺点:为了保证数组有序,在添加新数据时,找到插入位置后,后面的数据需整体移动,速度慢。
- 使用链式存储 - 链表:不管链表是否有序,查找速度都慢,但添加数据速度比数组快,不需要数据整体移动。
- 使用二叉排序树
# 4.2、二叉排序树介绍
- 二叉排序树:BST (Binary Sort (Search) Tree) ,对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大。
- 特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点
- 二叉树的中序遍历为有序数列
- 比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ,对应的二叉排序树为:
# 4.3、二叉排序树思路分析
# 4.3.1、添加子节点
-
假设待添加的节点为 node ,当前遍历的节点为 curNode,编码思路如下:
-
待添加节点 node 的值与当前节点 curNode 的值比较
node.value < curNode.value:需要将 node 节点安排在 curNode 节点的左边,左移当前节点指针:curNode = curNode.left ,为下次判断做准备node.value >= curNode.value:需要将 node 节点安排在 curNode 节点的右边,右移当前节点指针:curNode = curNode.right ,为下次判断做准备- 重复执行上述操作即可
-
何时停止递归?以下两个条件均可以让递归停止
-
待添加节点 node 的值比当前节点 curNode 的值小,并且 curNode 没有左节点
node.value < curNode.value && curNode.left ==null -
待添加节点 node 的值比当前节点 curNode 的值大(或相等),并且 curNode 没有右节点
node.value >= curNode.value && curNode.right==null
-
-
-
总结:新添加的节点都会沉到最下面去,成为一个叶子节点
# 4.3.2、查找子节点
- 查找目标子节点:假设目标节点的值为 value ,当前遍历的节点为 curNode ,编码思路如下
- 目标值 value 与当前节点值 curNode.value 进行比较
value == curNode.value:证明当前节点就是要找的节点,直接返回 curNodevalue < curNode.value:证明要找的节点在 curNode 左边,左移当前节点指针:curNode = curNode.left,并继续执行上述比较操作value >= curNode.value:证明要找的节点在 curNode 右边,右移当前节点指针:curNode = curNode.right,并继续执行上述比较操作
- 何时停止递归?
- 当前节点值与目标值相等:
curNode.value == value,证明当前节点就是要找的节点,直接返回 curNode - 或者当前节点为空:
curNode == null,即证明没找到,返回 null
- 当前节点值与目标值相等:
- 目标值 value 与当前节点值 curNode.value 进行比较
- 查找目标子节点的父节点(删除节点时需要查找目标节点的父节点):假设目标节点的值为 value ,当前遍历的节点为 parentNode ,parentNode 表示目标节点的父节点,编码思路如下
- 已找到目标节点的父节点:
- 如果:
parentNode.left != null && value = parentNode.left.value,则说明parent.left为目标节点,parent为目标节点的父节点 - 如果:
parentNode.right != null && value = parentNode.right.value,则说明parent.right为目标节点,parent为目标节点的父节点
- 如果:
- 还未找到目标节点的父节点,判断目标值 value 与当前节点值 parentNode.value 的大小
value < this.value && this.left != null:目标值在当前节点的左边,并且当前节点还有左节点,则将当前节点指针左移parentNode = parentNode.left,继续寻找目标节点value >= this.value && this.left != null:目标值在当前节点的右边,并且当前节点还有右节点,则将当前节点指针右移parentNode = parentNode.right,继续寻找目标节点
- 何时停止递归?两个递归停止条件,满足其中一个即可
- value = parentNode.left.value || value = parentNode.right.value :找到目标节点的父节点,则直接返回 parentNode
- 找不到目标节点的父节点:往左找找不到,往右找也找不到,
- 已找到目标节点的父节点:
# 4.3.3、删除子节点
- 再来一遍:
- 单链表能不能实现自删除?不能!
- 单链表想要删除需要怎么操作?找到其父节点!!!
- 假设目标节点的值为 value ,根节点为 root ,首先根据 value 值找到目标节点 targetNode ,再找到目标节点的父节点 parentNode
- 如果
targetNode == null,说明没有找到目标节点,直接滚蛋 - 如果
targetNode != null && root.left == null && root.right == null,说明只有根节点既是目标节点,删除根节点即可 - 否则就是下面三种复杂的情况咯:
- 如果
- 第一种情况:待删除的节点为叶子节点,直接删除该叶子节点即可
- 怎么样才算是叶子节点?
targetNode.left == null && targetNode.right == null:左右节点都为空 - 怎么删除?
- 如果
parentNode.left != null && parentNode.left.value == value:即待删除的节点是 parentNode 的左子节点,则删除 parentNode 的左节点:parentNode.left = null; - 如果
parentNode.right!= null && parentNode.right.value == value:即待删除的节点是 parentNode 的右子节点,则删除 parentNode 的右节点:parentNode.right= null;
- 如果
- 怎么样才算是叶子节点?
- 第二种情况:待删除的节点只有一颗子树,直接将其子树接在 parentNode 左边或右边即可
- 怎么判断节点只有一颗子树?targetNode.left 和 targetNode.right 中有且仅有一个为 null
- 怎么删除?四种情况
- 如果 targetNode 只有左子结点,则证明子树挂在 targetNode 的左边,现在来看看 target 挂在 parentNode 的哪边?
- 如果 target 挂在 parentNode 的左边,直接将 target 的子树挂在 parentNode 的左边:
parentNode.left = target.left - 如果 target 挂在 parentNode 的右边,直接将 target 的子树挂在 parentNode 的右边:
parentNode.right = target.left
- 如果 target 挂在 parentNode 的左边,直接将 target 的子树挂在 parentNode 的左边:
- 如果 targetNode 只有右子结点,则证明子树挂在 targetNode 的右边,现在来看看 target 挂在 parentNode 的哪边?
- 如果 target 挂在 parentNode 的左边,直接将 target 的子树挂在 parentNode 的左边:
parentNode.left = target.right - 如果 target 挂在 parentNode 的右边,直接将 target 的子树挂在 parentNode 的右边:
parentNode.right = target.right
- 如果 target 挂在 parentNode 的左边,直接将 target 的子树挂在 parentNode 的左边:
- 如果 targetNode 只有左子结点,则证明子树挂在 targetNode 的左边,现在来看看 target 挂在 parentNode 的哪边?
- 以上逻辑有个 Bug ~~~ 当待删除的节点为根节点时 ,
parentNode == null,这时候我们直接用根节点 root 来操作即可
- 第三种情况:待删除的节点具有两棵颗子树
- 从 targetNode 的左子树种找到值最大的节点(一直往右遍历),或者从从 targetNode 的右树种找到值最小的节点(一直往左遍历),假设最小值为 temp ,最小值所在的节点为 minNode
- 此时 minNode 肯定为叶子节点,删除 minNode 节点
- 将
targetNode.value设置为 temp ,这样以 targetNode 根节点的子树又是一棵二叉排序树
# 4.4、二叉排序树代码
# 4.4.1、树节点的定义
- 树节点的定义
//创建Node结点
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
// 添加结点的方法
// 递归的形式添加结点,注意需要满足二叉排序树的要求
public void add(Node node) {
if (node == null) {
return;
}
// 判断传入的结点的值,和当前子树根结点值的关系
if (node.value < this.value) {
// 如果当前结点左子结点为null
if (this.left == null) {
this.left = node;
} else {
// 递归的向左子树添加
this.left.add(node);
}
} else { // 添加的结点的值大于 当前结点的值
if (this.right == null) {
this.right = node;
} else {
// 递归的向右子树添加
this.right.add(node);
}
}
}
// 查找要删除的结点
/**
*
* @param value 希望删除的结点的值
* @return 如果找到返回该结点,否则返回null
*/
public Node search(int value) {
if (value == this.value) { // 找到就是该结点
return this;
} else if (value < this.value) {// 如果查找的值小于当前结点,向左子树递归查找
// 如果左子结点为空
if (this.left == null) {
return null;
}
return this.left.search(value);
} else { // 如果查找的值不小于当前结点,向右子树递归查找
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
// 查找要删除结点的父结点
/**
*
* @param value 要找到的结点的值
* @return 返回的是要删除的结点的父结点,如果没有就返回null
*/
public Node searchParent(int value) {
// 如果当前结点就是要删除的结点的父结点,就返回
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
// 如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
if (value < this.value && this.left != null) {
return this.left.searchParent(value); // 向左子树递归查找
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value); // 向右子树递归查找
} else {
return null; // 没有找到父结点
}
}
}
}# 4.4.2、二叉排序树的定义
- 二叉排序树的定义
//创建二叉排序树
class BinarySortTree {
private Node root;
public Node getRoot() {
return root;
}
// 添加结点的方法
public void add(Node node) {
if (root == null) {
root = node;// 如果root为空则直接让root指向node
} else {
root.add(node);
}
}
// 中序遍历
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("二叉排序树为空,不能遍历");
}
}
// 查找要删除的结点
public Node search(int value) {
if (root == null) {
return null;
} else {
return root.search(value);
}
}
// 查找父结点
public Node searchParent(int value) {
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
// 删除结点
public void delNode(int value) {
if (root == null) {
return;
} else {
// 1.需求先去找到要删除的结点 targetNode
Node targetNode = search(value);
// 如果没有找到要删除的结点
if (targetNode == null) {
return;
}
// 如果我们发现当前这颗二叉排序树只有一个结点
if (root.left == null && root.right == null) {
root = null;
return;
}
// 去找到targetNode的父结点
Node parent = searchParent(value);
// 如果要删除的结点是叶子结点
if (targetNode.left == null && targetNode.right == null) {
// 判断targetNode 是父结点的左子结点,还是右子结点
if (parent.left != null && parent.left.value == value) { // 是左子结点
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {// 是右子结点
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
} else { // 删除只有一颗子树的结点
// 如果要删除的结点有左子结点
if (targetNode.left != null) {
if (parent != null) {
// 如果 targetNode 是 parent 的左子结点
if (parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode 是 parent 的右子结点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { // 如果要删除的结点有右子结点
if (parent != null) {
// 如果 targetNode 是 parent 的左子结点
if (parent.left.value == value) {
parent.left = targetNode.right;
} else { // 如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
// 编写方法:
// 1. 返回的 以node 为根结点的二叉排序树的最小结点的值
// 2. 删除node 为根结点的二叉排序树的最小结点
/**
*
* @param node 传入的结点(当做二叉排序树的根结点)
* @return 返回的 以node 为根结点的二叉排序树的最小结点的值
*/
public int delRightTreeMin(Node node) {
Node target = node;
// 循环的查找左子节点,就会找到最小值
while (target.left != null) {
target = target.left;
}
// 这时 target就指向了最小结点
// 删除最小结点(该节点肯定是左叶子节点)
delNode(target.value);
return target.value;
}
}# 4.4.3、代码测试
- 代码
public static void main(String[] args) {
int[] arr = { 7, 3, 10, 12, 5, 1, 9, 2 };
BinarySortTree binarySortTree = new BinarySortTree();
// 循环的添加结点到二叉排序树
for (int i = 0; i < arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
// 中序遍历二叉排序树
System.out.println("中序遍历二叉排序树~");
binarySortTree.infixOrder(); // 1, 3, 5, 7, 9, 10, 12
// 测试一下删除叶子结点
binarySortTree.delNode(5);
binarySortTree.delNode(10);
System.out.println("删除结点后");
binarySortTree.infixOrder();
}- 程序运行结果
中序遍历二叉排序树~
Node [value=1]
Node [value=2]
Node [value=3]
Node [value=5]
Node [value=7]
Node [value=9]
Node [value=10]
Node [value=12]
删除结点后
Node [value=1]
Node [value=2]
Node [value=3]
Node [value=7]
Node [value=9]
Node [value=12]# 4.5、课后练习
- 如果我们从左子树找到最大的结点, 然后前面的思路完成.
# 5、平衡二叉树 (AVL 树)
# 5.1、二叉排序树的问题
- 看一个案例 (说明二叉排序树可能的问题),给你一个数列 { 1,2,3,4,5,6 } ,要求创建一颗二叉排序树 (BST),并分析问题所在
- 左子树全部为空,从形式上看,更像一个单链表
- 插入速度没有影响
- 查询速度明显降低 (因为需要依次比较),不能发挥 BST 的优势,因为每次还需要比较左子,其查询速度比单链表还慢
- 解决方案 - 平衡二叉树 (AVL)
# 5.2、平衡二叉树基本介绍
- 平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为 AVL 树, 可以保证查询效率较高。
- 平衡二叉树具有以下特点:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。
- 平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
- 注意:平衡二叉树一定是二叉排序树!!!
- 举例说明,看看下面哪些 AVL 树,为什么?
# 5.3、平衡二叉树思路分析
# 5.3.1、计算子树高度
- 其实计算子树高度这个递归还挺难理解的,我想了想,可以这样来理解:
left == null ? 0 : left.height()是求左子树的高度right == null ? 0 : right.height()是求右子树的高度- 所以如上两个表达式取最大值,即为当前子树的高度
// 返回 以该结点为根结点的树的高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}- 画了个图来说明计算子树高度的递归顺序和递归回溯过程
# 5.3.2、左旋转
-
问题:当插入 8 时,
rightHeight() - leftHeight() > 1成立,此时,不再是一颗 AVL 树了 -
怎么处理–进行左旋转(就是降低右子树的高度)
- 创建一个新的节点 newNode (以 4 这个值创建),创建一个新的节点,值等于当前根节点的值
- 把新节点的左子树设置了当前节点的左子树:
newNode.left = left - 把新节点的右子树设置为当前节点的右子树的左子树:
newNode.right =right.left; - 把当前节点的值换为右子节点的值:
value=right.value; - 把当前节点的右子树设置成右子树的右子树:
right=right.right; - 把当前节点的左子树设置为新节点:
left=newNode;
-
想想为啥是上面的的步骤?
- 插入节点 8 后,整棵树不再是 AVL 树,节点 4 的右子树高度 > 节点 4 的左子树高度,需要进行左旋
- 问题来了:什么是左旋?怎么进行左旋?还是以下面的图为例:不就是把节点 6 往上提,把根节点 4 往左下沉,然后再把节点 5 挂在节点 4 的右边
# 5.3.3、右旋转
-
问题:当插入 6 时,
leftHeight() - rightHeight() > 1成立,此时,不再是一颗 AVL 树了 -
怎么处理–进行右旋转(就是降低左子树的高度) 这里是将 9 这个节点,通过右旋转,到右子树
-
创建一个新的节点 newNode (以 10 这个值创建) ,创建一个新的节点,值等于当前根节点的值
-
把新节点的右子树设置了当前节点的右子树:
newNode.right = right; -
把新节点的左子树设置为当前节点的左子树的右子树:
newNode.left =left.right; -
把当前节点的值换为左子节点的值:
value=left.value; -
把当前节点的左子树设置成左子树的左子树:
left=left.left; -
把当前节点的右子树设置为新节点:
right=newNode;
-
想想为啥是上面的的步骤?
- 插入节点 6 后,整棵树不再是 AVL 树,节点 10 的左子树高度 > 节点 10 的右子树高度,需要进行右旋
- 问题来了:什么是右旋?怎么进行右旋?还是以下面的图为例:不就是把节点 8 往上提,把根节点 10 往右下沉,然后把节点 9 挂在节点 10 的左边
# 5.3.4、双旋转
- 问题分析
- 如下不平衡二叉树满足右旋条件,根节点 10 的左子树高度 > 根节点的右子树高度
- 但不巧的是:根节点 10 的左子树的右子树高度 > 根节点 10 的左子树的左子树高度,那么在进行右旋后,还是棵不平衡二叉树
- 那不就是因为节点 7 的右子树太长了,进行右旋后,挂到右边去会导致整棵树的右子树过高
- 怎么解决?
- 目标:把节点 7 的右子树的高度降低,即对节点 7 进行左旋
- 我先把以节点 7 为根节点的树搞成 AVL 树(对节点 7 进行左旋),再对节点 10 进行右旋,就行啦~
- 即先对当前结点的左节点进行左旋转,再对当前结点进行右旋转的操作即可
- 编码思路:假设当前节点为 curNode
- 如果
curNode.rightHeight() - curNode.leftHeight() > 1:需进行左旋- 如果
curNode.left.leftHeight() > curNode.left.rightHeight()- 先对
curNode.left进行右旋:curNode.left.rightRotate() - 再对
curNode进行左旋:curNode.leftRotate()
- 先对
- 否则直接进行左旋:
curNode.leftRotate()
- 如果
- 如果
curNode.leftHeight() - curNode.rightHeight() > 1:需进行右旋- 如果
curNode.left.rightHeight() > curNode.left.leftHeight()- 先对
curNode.left进行左旋:curNode.left.leftHeight() - 再对 curNode 进行右旋:
curNode.rightRotate()
- 先对
- 否则直接进行右旋:
curNode.rightRotate()
- 如果
- 如果
- 图有点难看,有时间再重新画吧。。。
# 5.4、平衡二叉树代码
# 5.4.1、树节点的定义
// 创建Node结点
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
// 返回左子树的高度
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
// 返回右子树的高度
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
// 返回 以该结点为根结点的树的高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
// 左旋转方法
private void leftRotate() {
// 创建新的结点,以当前根结点的值
Node newNode = new Node(value);
// 把新的结点的左子树设置成当前结点的左子树
newNode.left = left;
// 把新的结点的右子树设置成当前结点的右子树的左子树
newNode.right = right.left;
// 把当前结点的值替换成右子结点的值
value = right.value;
// 把当前结点的右子树设置成当前结点右子树的右子树
right = right.right;
// 把当前结点的左子树(左子结点)设置成新的结点
left = newNode;
}
// 右旋转
private void rightRotate() {
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
// 添加结点的方法
// 递归的形式添加结点,注意需要满足二叉排序树的要求
public void add(Node node) {
if (node == null) {
return;
}
// 判断传入的结点的值,和当前子树的根结点的值关系
if (node.value < this.value) {
// 如果当前结点左子结点为null
if (this.left == null) {
this.left = node;
} else {
// 递归的向左子树添加
this.left.add(node);
}
} else { // 添加的结点的值大于 当前结点的值
if (this.right == null) {
this.right = node;
} else {
// 递归的向右子树添加
this.right.add(node);
}
}
// 当添加完一个结点后,如果: (右子树的高度-左子树的高度) > 1 , 左旋转
if (rightHeight() - leftHeight() > 1) {
// 如果它的右子树的左子树的高度大于它的右子树的右子树的高度
if (right != null && right.leftHeight() > right.rightHeight()) {
// 先对右子结点进行右旋转
right.rightRotate();
// 然后在对当前结点进行左旋转
leftRotate(); // 左旋转..
} else {
// 直接进行左旋转即可
leftRotate();
}
return; // 必须要!!!
}
// 当添加完一个结点后,如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
if (leftHeight() - rightHeight() > 1) {
// 如果它的左子树的右子树高度大于它的左子树的高度
if (left != null && left.rightHeight() > left.leftHeight()) {
// 先对当前结点的左结点(左子树)->左旋转
left.leftRotate();
// 再对当前结点进行右旋转
rightRotate();
} else {
// 直接进行右旋转即可
rightRotate();
}
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
}# 5.4.2、平衡二叉树的定义
// 创建AVLTree
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
// 添加结点的方法
public void add(Node node) {
if (root == null) {
root = node;// 如果root为空则直接让root指向node
} else {
root.add(node);
}
}
// 中序遍历
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("二叉排序树为空,不能遍历");
}
}
}# 5.4.3、代码测试
- 代码
public static void main(String[] args) {
int[] arr = { 10, 11, 7, 6, 8, 9 };
// 创建一个 AVLTree对象
AVLTree avlTree = new AVLTree();
// 添加结点
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
// 遍历
System.out.println("中序遍历");
avlTree.infixOrder();
System.out.println("平衡处理后~~");
System.out.println("树的高度=" + avlTree.getRoot().height()); // 3
System.out.println("树的左子树高度=" + avlTree.getRoot().leftHeight()); // 2
System.out.println("树的右子树高度=" + avlTree.getRoot().rightHeight()); // 2
System.out.println("当前的根结点=" + avlTree.getRoot());// 8
System.out.println("根节点的左结点=" + avlTree.getRoot().left);// 7
System.out.println("根节点的右结点=" + avlTree.getRoot().right);// 10
}- 程序运行结果
中序遍历
Node [value=6]
Node [value=7]
Node [value=8]
Node [value=9]
Node [value=10]
Node [value=11]
平衡处理后~~
树的高度=3
树的左子树高度=2
树的右子树高度=2
当前的根结点=Node [value=8]
根节点的左结点=Node [value=7]
根节点的右结点=Node [value=10]# 多路查找树
# 1、二叉树与 B 树
# 1.1、二叉树存在的问题
- 二叉树的操作效率较高,但是也存在问题,请看下面的二叉树
- 二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多 (比如 1 亿), 就存在如下问题:
- 问题 1:在构建二叉树时,需要多次进行 i/o 操作 (海量数据存在数据库或文件中),节点海量,构建二叉树时,速度有影响
- 问题 2:节点海量,也会造成二叉树的高度很大,会降低操作速度
# 1.2、多叉树的基本介绍
- 在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,就是多叉树(multiway tree)
- 后面我们讲解的 2-3 树,2-3-4 树就是多叉树,多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化
- 举例说明 (下面 2-3 树就是一颗多叉树)
# 1.3、B 树的基本介绍
- B 树通过重新组织节点,降低树的高度,并且减少 i/o 读写次数来提升效率。
- 如图 B 树通过重新组织节点, 降低了树的高度。
- 文件系统及数据库系统的设计者利用了磁盘预读原理,将一个节点的大小设为等于一个页 (页的大小通常为 4k),这样每个节点只需要一次 I/O 就可以完全载入
- 将树的度 M 设置为 1024,在 600 亿个元素中最多只需要 4 次 I/O 操作就可以读取到想要的元素,B 树 (B+) 广泛应用于文件存储系统以及数据库系统中
# 1.4、2-3 树基本介绍
# 1.4.1、2-3 应用案例
-
2-3 树是最简单的 B 树结构,具有如下特点:
- 2-3 树的所有叶子节点都在同一层 (只要是 B 树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点
-
2-3 树是由二节点和三节点构成的树。
-
2-3 树插入规则:
- 2-3 树的所有叶子节点都在同一层 (只要是 B 树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点
- 当按照规则插入一个数到某个节点时,不能满足上面三个要求,就需要拆,先向上拆,如果上层满,则拆本层,拆后仍然需要满足上面 3 个条件。
- 对于三节点的子树的值大小仍然遵守 (BST 二叉排序树) 的规则
-
将数列 {16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20} 构建成 2-3 树,并保证数据插入的大小顺序,演示一下构建 2-3 树的过程
-
插入 24 时,构成二节点
-
插入 12 时
- 不能将其放在 16 的左边,这样就是四节点了。。。
- 不能直接挂在 16 的左下位置,这样就不满足【2-3 树的所有叶子节点都在同一层】这个条件
- 所以需要拆掉上一层的节点,将其重新组合成 2-3 树
- 插入 32 时,可直接放在 24 的右边,构成一个三节点
- 插入 26 时
- 不能将其放在 24 的右边,这样就是四节点了。。。
- 不能直接挂在 24 的右下位置,这样就不满足 B 树的条件
- 所以需要拆掉上一层的节点,将其重新组合成 2-3 树
- 插入 34 时
- 插入 10 时
- 当插入 10 时,应当在 10 - 12 -14 这个位置,但是这时满了,因此向上层看, 16-26 也满了
- 因此将 10-12-14 拆 成 10 <-12->14 ,因为其它拆法,并不能满足 二节点或三节点的要求
- 但是这时,叶子节点没有全部在同一层,需要调整 26 这个值到下面 (如图)
- 插入 8 时
- 插入 28 时
- 插入 38 时
- 插入 20 时
-
# 1.4.2、其他说明
- 除了 2-3 树,还有 2-3-4 树等,概念和 2-3 树类似,也是一种 B 树。 如图:
# 1.5、B 树的介绍
-
B-tree 树即 B 树,B 即 Balanced ,平衡的意思。有人把 B-tree 翻译成 B- 树,容易让人 产生误解。会以为 B- 树是一种树,而 B 树又是另一种树。实际上,B-tree 就是指的 B 树。
-
前面已经介绍了 2-3 树和 2-3-4 树,他们就是 B 树 (英语:B-tree 也写成 B - 树),这里我们再做一个说明,我们在学习 Mysql 时,经常听到说某种类型的索引是基于 B 树或者 B + 树的,如图
-
B 树的说明:
- B 树的阶(度):节点的最多子节点个数。比如 2-3 树的阶是 3,2-3-4 树的阶是 4
- B 树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点
- 关键字集合分布在整颗树中,即叶子节点和非叶子节点都存放数据
- 搜索有可能在非叶子结点结束
- 其搜索性能等价于在关键字全集内做一次二分查找
# 1.6、B+ 树的介绍
-
B + 树是 B 树的变体,也是一种多路搜索树。
-
B + 树的说明:
- B + 树的搜索与 B 树也基本相同,区别是 B + 树只有达到叶子结点才命中(B 树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找
- 所有关键字都出现在叶子结点的链表中(即数据只能在叶子节点【也叫稠密索引】),且链表中的关键字 (数据) 恰好是有序的。
- 不可能在非叶子结点命中
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
- B + 树的所有叶结点构成一个有序链表,可以按照关键码排序的次序遍历全部记录
- B + 树更适合文件索引系统,B 树和 B + 树各有自己的应用场景,不能说 B + 树完全比 B 树好,反之亦然
- 自己对 B+ 树的理解:
- 就拿有序数列 {8, 10, 12, 14, 16, 20, 24, 26, 28, 32, 34, 38} 来说,如果链表形式存储,搜索效率肯定低得一匹
- 但是有没有什么方法可以改进呢?一种就是前面所说的二叉树,还有一种就是现在说的 B+ 树
- B+ 树到底是什么个意思?比如说我们想要查找 28 这个数,从前面挨个往后查找肯定是不行滴,但是我们知道 28 肯定是在 26 和 38 之间,有这个思路就可以了
- 我们手动将 {8, 10, 12, 14, 16, 20, 24, 26, 28, 32, 34, 38} 分成几个区间,查找 28 时,直接去他所在区间查不就快得多了吗?这个所谓的区间,也就是我们常说的索引
# 1.7、B* 树的介绍
- B* 树是 B + 树的变体,在 B + 树的非根和非叶子结点再增加指向兄弟的指针。
- B* 树的说明:
- B* 树定义了非叶子结点关键字个数至少为 (2/3)*M,即块的最低使用率为 2/3,而 B + 树的块的最低使用率为 B + 树的 1/2。
- 从第 1 个特点我们可以看出,B* 树分配新结点的概率比 B + 树要低,空间使用率更高
# 图
# 1、图基本介绍
# 1.1、为什么要有图
- 前面我们学了线性表和树
- 线性表局限于一个直接前驱和一个直接后继的关系
- 树也只能有一个直接前驱也就是父节点
- 当我们需要表示多对多的关系时, 这里我们就用到了图
# 1.2、图的举例说明
- 图是一种数据结构,其中结点可以具有零个或多个相邻元素。两个结点之间的连接称为边。 结点也可以称为顶点。如图:
# 1.3、图的常用概念
- 顶点 (vertex)
- 边 (edge)
- 路径
- 无向图 (右图)
- 无向图: 顶点之间的连接没有方向,比如 A-B,即可以是 A-> B 也可以 B->A
- 路径:比如从 D -> C 的路径有
- D->B->C
- D->A->B->C
- 有向图:顶点之间的连接有方向,比如 A-B,只能是 A-> B 不能是 B->A
- 带权图:这种边带权值的图也叫网
# 2、图的表示方式
- 图的表示方式有两种:二维数组表示(邻接矩阵);链表表示(邻接表)
# 2.1、邻接矩阵
- 邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于 n 个顶点的图而言,矩阵是的 row 和 col 表示的是 1…n 个点
# 2.2、邻接表
- 邻接矩阵需要为每个顶点都分配 n 个边的空间,其实有很多边都是不存在,会造成空间的一定损失
- 邻接表的实现只关心存在的边,不关心不存在的边。因此没有空间浪费,邻接表由数组 + 链表组成
- 邻接表说明:
- 标号为 0 的结点的相关联的结点为 1 2 3 4
- 标号为 1 的结点的相关联结点为 0 4
- 标号为 2 的结点相关联的结点为 0 4 5
- …
# 3、图的创建
# 3.1、代码思路
- 邻接矩阵法:
- 存储顶点:ArrayList
- 存储矩阵:
int[][] - 存储边数:Integer
# 3.2、图的定义
- 图的定义:
- vertexList :存储顶点集合
- edges :邻结矩阵
- numOfEdges :边的数目(每添加一条边,numOfEdges 加一)
class Graph {
private ArrayList<String> vertexList; //存储顶点集合
private int[][] edges; //存储图对应的邻结矩阵
private int numOfEdges; //表示边的数目
//构造器
public Graph(int n) {
//初始化矩阵和vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
//插入结点
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//添加边
/**
*
* @param v1 第二个顶点对应的下标
* @param v2 第二个顶点对应的下标
* @param weight 表示权值,0:不连接;1:连接
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
//图中常用的方法
//返回结点的个数
public int getNumOfVertex() {
return vertexList.size();
}
// 得到边的数目
public int getNumOfEdges() {
return numOfEdges;
}
// 返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
// 返回v1和v2的权值
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
// 显示图对应的矩阵
public void showGraph() {
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
}# 3.3、代码测试
- 代码
public static void main(String[] args) {
//测试一把图是否创建ok
String Vertexs[] = {"A", "B", "C", "D", "E"};
int n = Vertexs.length; //结点的个数
// String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"};
//创建图对象
Graph graph = new Graph(n);
//循环的添加顶点
for(String vertex: Vertexs) {
graph.insertVertex(vertex);
}
//添加边
//A-B A-C B-C B-D B-E
graph.insertEdge(0, 1, 1); // A-B
graph.insertEdge(0, 2, 1); // A-C
graph.insertEdge(1, 2, 1); // B-C
graph.insertEdge(1, 3, 1); // B-D
graph.insertEdge(1, 4, 1); // B-E
//显示一把邻结矩阵
graph.showGraph();
}- 程序运行结果
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]# 4、图的遍历
# 4.1、深度优先和广度优先
- 图遍历介绍:所谓图的遍历,即是对结点的访问。一个图有那么多个结点,如何遍历这些结点,需要特定策略,一般有两种访问策略:
- 深度优先遍历
- 广度优先遍历
# 4.2、图的深度优先遍历
-
深度优先遍历基本思想,图的深度优先搜索 (Depth First Search)
- 深度优先遍历,从初始访问结点出发,初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点, 可以这样理解:每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
- 我们可以看到,这样的访问策略是优先往纵向挖掘深入,而不是对一个结点的所有邻接结点进行横向访问。
-
显然,深度优先搜索是一个递归的过程
# 4.2.1、代码思路
-
深度优先遍历算法步骤
- 访问初始结点 v ,并标记结点 v 为已访问。
- 查找结点 v 的第一个邻接结点 w
- 如果 w 存在
- 如果 w 未被访问过,先标记 w 已被访问过,然后把 w 当做下一个 v ,查找 w 的第一个邻接点,继续执行深度遍历(这是个递归的过程)
- 如果 w 已经被访问过,则跳过此节点
- 如果 w 不存在,说明 v 真的没有下一个邻接点了,已经到头了,我们回到节点 v ,将从 v 的下一个结点继续查找
- 如果 w 存在
- 经过如上步骤,图中可能还有其他顶点未被访问,继续从下一个顶点执行如上操作
- 如何找到当前顶点的下一个邻接点?
- 假设当前正在遍历的顶点索引为 i ,顶点 i 的边信息存储在
edges[][]数组中第 i 行 - 假设顶点 i 的当前遍历到的邻接点索引为 j ,即已经遍历到了 第
edges[i][j]处,需要从edges[i][j]之后去找顶点 i 的下一个邻接点索引
- 假设当前正在遍历的顶点索引为 i ,顶点 i 的边信息存储在
-
举例说明:
- 访问顶点 A 后输出 A ,A 的第一个邻接点是 B ,B 未被访问过,我们访问顶点 B
- 访问顶点 B 后输出 A–> B
- B 的第一个邻接点 A 已经被访问过了
- B 的第二个邻接点 C 还未被访问过,我们访问节点 C
- 访问节点 C
- C 的第一个邻接点是 A ,然而 A 已经访问过了
- C 的下一个邻接点是 B ,然而 B 也已经访问过了
- 除此之外,C 再也没有其他邻接点
- 我们回到顶点 B ,访问节点 B 的下一个邻接点:顶点 D
- 访问顶点 D 后输出 A --> B --> C --> D ,D 没有邻接节点,所以又返回到顶点 B ,访问顶点 B 的下一个邻接点:顶点 E
- 访问顶点 E 后输出 A --> B --> C --> D --> E,E 没有邻接节点,所以又返回到顶点 B
- B 的所有邻接点都访问过了,返回到顶点 A
- 以上所有操作仅是一轮,还需要再对图中其他顶点进行以上操作
- 总结:
- 假设初始状态是图中所有顶点均未被访问,则从某个顶点 v 出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和 v 有路径相通的顶点都被访问到。
- 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点(额,我实在想不到这种特例),重复上述过程,直至图中所有顶点都被访问到为止。
# 4.2.2、代码实现
- 编写图的深度优先遍历
class Graph {
private ArrayList<String> vertexList; //存储顶点集合
private int[][] edges; //存储图对应的邻结矩阵
private int numOfEdges; //表示边的数目
//构造器
public Graph(int n) {
//初始化矩阵和vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
//插入结点
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//添加边
/**
*
* @param v1 第二个顶点对应的下标
* @param v2 第二个顶点对应的下标
* @param weight 表示权值,0:不连接;1:连接
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
//图中常用的方法
//返回结点的个数
public int getNumOfVertex() {
return vertexList.size();
}
// 得到边的数目
public int getNumOfEdges() {
return numOfEdges;
}
// 返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
// 返回v1和v2的权值
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
// 显示图对应的矩阵
public void showGraph() {
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
//得到第一个邻接结点的下标 w
/**
*
* @param index
* @return 如果存在就返回对应的下标,否则返回-1
*/
public int getFirstNeighbor(int index) {
for(int j = 0; j < vertexList.size(); j++) {
if(edges[index][j] > 0) {
return j;
}
}
return -1;
}
//根据前一个邻接结点的下标来获取下一个邻接结点
public int getNextNeighbor(int v1, int v2) {
for(int j = v2 + 1; j < vertexList.size(); j++) {
if(edges[v1][j] > 0) {
return j;
}
}
return -1;
}
//深度优先遍历算法
//i 第一次就是 0
private void dfs(boolean[] isVisited, int i) {
//首先我们访问该结点,输出
System.out.print(getValueByIndex(i) + "->");
//将结点设置为已经访问
isVisited[i] = true;
//查找结点i的第一个邻接结点w
int w = getFirstNeighbor(i);
while(w != -1) {//说明有
if(!isVisited[w]) {
dfs(isVisited, w);
}
//如果w结点已经被访问过
w = getNextNeighbor(i, w);
}
}
//对dfs 进行一个重载, 遍历我们所有的结点,并进行 dfs
public void dfs() {
boolean[] isVisited = new boolean[vertexList.size()];
//遍历所有的结点,进行dfs[回溯]
for(int i = 0; i < getNumOfVertex(); i++) {
if(!isVisited[i]) {
dfs(isVisited, i);
}
}
}
}- 测试代码
public static void main(String[] args) {
//测试一把图是否创建ok
String Vertexs[] = {"A", "B", "C", "D", "E"};
int n = Vertexs.length; //结点的个数
// String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"};
//创建图对象
Graph graph = new Graph(n);
//循环的添加顶点
for(String vertex: Vertexs) {
graph.insertVertex(vertex);
}
//添加边
//A-B A-C B-C B-D B-E
graph.insertEdge(0, 1, 1); // A-B
graph.insertEdge(0, 2, 1); // A-C
graph.insertEdge(1, 2, 1); // B-C
graph.insertEdge(1, 3, 1); // B-D
graph.insertEdge(1, 4, 1); // B-E
//显示一把邻结矩阵
graph.showGraph();
//测试一把,我们的dfs遍历是否ok
System.out.println("深度遍历");
graph.dfs(); // A->B->C->D->E
}- 程序运行结果
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
深度遍历
A->B->C->D->E-># 4.3、图的广度优先遍历
# 4.3.1、代码思路
- 图的广度优先搜索 (Broad First Search) ,类似于一个分层搜索的过程,广度优先遍历需要使用一个队列以保持访问过的结点的顺序,以便按这个顺序来访问这些结点的邻接结点
- 广度优先遍历的编码流程:
- 访问当前顶点 v 并标记结点 v 为已访问,并将顶点 v 入队
- 将顶点 v 出队,并在同一层搜索顶点 v 的邻接点,将没有访问过的邻接点其加入队列中,说明这些邻接点待访问
- 以队列头部的顶点作为新的顶点 v ,并进行与之前相同的操作:将顶点 v 出队 …
- 直至队列为空
- 经过如上步骤,图中可能还有其他顶点未被访问,继续从下一个顶点执行如上操作
-
举例说明:
- 访问顶点 A 后输出 A ,并将顶点 A 压入队列中
- 开始不断循环,循环条件:队列不为空
- 将顶点 A 出队,找到顶点的的所有邻接点:顶点 B 和顶点 C ,顶点 B 和顶点 C 均没有被访问过,将其入队
- 队列不为空,将队列头(顶点 B)取出,顶点 B 的邻接点为:顶点 C 、顶点 D 、顶点 E ,顶点 C 已经访问过了,不再添加至队列中,顶点 D 和顶点 E 均没有被访问过,将其入队
- 队列不为空,将队列头(顶点 C)取出,顶点 C 的邻接点为:顶点 A 和顶点 B ,顶点 A 和顶点 B 均被访问过,不再添加至队列
- 队列不为空,将队列头(顶点 D)取出,D 没有邻接点,啥也不做
- 队列不为空,将队列头(顶点 E)取出,E 没有邻接点,啥也不做
- 队列为空,退出循环
- 以上所有操作仅是一轮,还需要再对图中其他顶点进行以上操作
-
总结:
- 从图中某顶点 v 出发,在访问了 v 之后依次访问 v 的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得 “先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。
- 如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
-
我把图重新画了一下,可以更好地理解广度优先遍历,即先把同一层顶点先遍历了,添加至队列中,再去到下一层
# 4.3.2、代码实现
- 编写图的广度优先遍历
class Graph {
private ArrayList<String> vertexList; // 存储顶点集合
private int[][] edges; // 存储图对应的邻结矩阵
private int numOfEdges; // 表示边的数目
// 构造器
public Graph(int n) {
// 初始化矩阵和vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
// 插入结点
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
// 添加边
/**
*
* @param v1 第二个顶点对应的下标
* @param v2 第二个顶点对应的下标
* @param weight 表示权值,0:不连接;1:连接
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
// 图中常用的方法
// 返回结点的个数
public int getNumOfVertex() {
return vertexList.size();
}
// 得到边的数目
public int getNumOfEdges() {
return numOfEdges;
}
// 返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
// 返回v1和v2的权值
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
// 显示图对应的矩阵
public void showGraph() {
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
// 得到第一个邻接结点的下标 w
/**
*
* @param index
* @return 如果存在就返回对应的下标,否则返回-1
*/
public int getFirstNeighbor(int index) {
for (int j = 0; j < vertexList.size(); j++) {
if (edges[index][j] > 0) {
return j;
}
}
return -1;
}
// 根据前一个邻接结点的下标来获取下一个邻接结点
public int getNextNeighbor(int v1, int v2) {
for (int j = v2 + 1; j < vertexList.size(); j++) {
if (edges[v1][j] > 0) {
return j;
}
}
return -1;
}
// 对一个结点进行广度优先遍历的方法
private void bfs(boolean[] isVisited, int i) {
int u; // 表示队列的头结点对应下标
int w; // 邻接结点w
// 队列,记录结点访问的顺序
LinkedList<Integer> queue = new LinkedList<Integer>();
// 访问结点,输出结点信息
System.out.print(getValueByIndex(i) + "=>");
// 标记为已访问
isVisited[i] = true;
// 将结点加入队列
queue.addLast(i);
while (!queue.isEmpty()) {// 体现出我们的广度优先
// 取出队列的头结点下标
u = queue.removeFirst();
// 得到第一个邻接结点的下标 w
w = getFirstNeighbor(u);
while (w != -1) {// 找到
// 是否访问过
if (!isVisited[w]) {
System.out.print(getValueByIndex(w) + "=>");
// 标记已经访问
isVisited[w] = true;
// 入队
queue.addLast(w);
}
// 以u为前驱点,找w后面的下一个邻结点
w = getNextNeighbor(u, w);
}
}
}
// 遍历所有的结点,都进行广度优先搜索
public void bfs() {
boolean[] isVisited = new boolean[vertexList.size()];
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
bfs(isVisited, i);
}
}
}
}- 测试代码
public static void main(String[] args) {
// 测试一把图是否创建ok
String Vertexs[] = { "A", "B", "C", "D", "E" };
int n = Vertexs.length; // 结点的个数
// String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"};
// 创建图对象
Graph graph = new Graph(n);
// 循环的添加顶点
for (String vertex : Vertexs) {
graph.insertVertex(vertex);
}
// 添加边
// A-B A-C B-C B-D B-E
graph.insertEdge(0, 1, 1); // A-B
graph.insertEdge(0, 2, 1); // A-C
graph.insertEdge(1, 2, 1); // B-C
graph.insertEdge(1, 3, 1); // B-D
graph.insertEdge(1, 4, 1); // B-E
// 显示一把邻结矩阵
graph.showGraph();
// 测试一把,我们的bfs遍历是否ok
System.out.println("广度优先");
graph.bfs(); // A->B->C->D->E
}- 程序运行结果
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
广度优先
A=>B=>C=>D=>E=># 4.4、深度 VS 广度优先
- 待遍历的图
- 创建图
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 1);
graph.insertEdge(1, 3, 1);
graph.insertEdge(1, 4, 1);
graph.insertEdge(3, 7, 1);
graph.insertEdge(4, 7, 1);
graph.insertEdge(2, 5, 1);
graph.insertEdge(2, 6, 1);
graph.insertEdge(5, 6, 1);-
理论输出顺序:
- 深度优先遍历顺序为 1->2->4->8->5->3->6->7
- 广度优先算法的遍历顺序为:1->2->3->4->5->6->7->8
-
测试代码
public class GraphDemo {
public static void main(String[] args) {
// 测试一把图是否创建ok
String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"};
int n = Vertexs.length; // 结点的个数
// 创建图对象
Graph graph = new Graph(n);
// 循环的添加顶点
for (String vertex : Vertexs) {
graph.insertVertex(vertex);
}
//更新边的关系
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 1);
graph.insertEdge(1, 3, 1);
graph.insertEdge(1, 4, 1);
graph.insertEdge(3, 7, 1);
graph.insertEdge(4, 7, 1);
graph.insertEdge(2, 5, 1);
graph.insertEdge(2, 6, 1);
graph.insertEdge(5, 6, 1);
//显示一把邻结矩阵
graph.showGraph();
//测试一把,我们的dfs遍历是否ok
System.out.println("深度遍历");
graph.dfs(); // [1->2->4->8->5->3->6->7]
System.out.println();
System.out.println("广度优先!");
graph.bfs(); // [1->2->3->4->5->6->7->8]
}
}- 程序运行结果
[0, 1, 1, 0, 0, 0, 0, 0]
[1, 0, 0, 1, 1, 0, 0, 0]
[1, 0, 0, 0, 0, 1, 1, 0]
[0, 1, 0, 0, 0, 0, 0, 1]
[0, 1, 0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0, 1, 0]
[0, 0, 1, 0, 0, 1, 0, 0]
[0, 0, 0, 1, 1, 0, 0, 0]
深度遍历
1->2->4->8->5->3->6->7->
广度优先!
1=>2=>3=>4=>5=>6=>7=>8=># 5、图遍历的全部代码
public class GraphDemo {
public static void main(String[] args) {
// 测试一把图是否创建ok
String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"};
int n = Vertexs.length; // 结点的个数
// 创建图对象
Graph graph = new Graph(n);
// 循环的添加顶点
for (String vertex : Vertexs) {
graph.insertVertex(vertex);
}
//更新边的关系
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 1);
graph.insertEdge(1, 3, 1);
graph.insertEdge(1, 4, 1);
graph.insertEdge(3, 7, 1);
graph.insertEdge(4, 7, 1);
graph.insertEdge(2, 5, 1);
graph.insertEdge(2, 6, 1);
graph.insertEdge(5, 6, 1);
//显示一把邻结矩阵
graph.showGraph();
//测试一把,我们的dfs遍历是否ok
System.out.println("深度遍历");
graph.dfs(); // [1->2->4->8->5->3->6->7]
System.out.println();
System.out.println("广度优先!");
graph.bfs(); // [1->2->3->4->5->6->7->8]
}
}
class Graph {
private ArrayList<String> vertexList; // 存储顶点集合
private int[][] edges; // 存储图对应的邻结矩阵
private int numOfEdges; // 表示边的数目
// 构造器
public Graph(int n) {
// 初始化矩阵和vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
// 插入结点
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
// 添加边
/**
*
* @param v1 第二个顶点对应的下标
* @param v2 第二个顶点对应的下标
* @param weight 表示权值,0:不连接;1:连接
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
// 图中常用的方法
// 返回结点的个数
public int getNumOfVertex() {
return vertexList.size();
}
// 得到边的数目
public int getNumOfEdges() {
return numOfEdges;
}
// 返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
// 返回v1和v2的权值
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
// 显示图对应的矩阵
public void showGraph() {
for (int[] link : edges) {
System.out.println(Arrays.toString(link));
}
}
// 得到第一个邻接结点的下标 w
/**
*
* @param index
* @return 如果存在就返回对应的下标,否则返回-1
*/
public int getFirstNeighbor(int index) {
for (int j = 0; j < vertexList.size(); j++) {
if (edges[index][j] > 0) {
return j;
}
}
return -1;
}
// 根据前一个邻接结点的下标来获取下一个邻接结点
public int getNextNeighbor(int v1, int v2) {
for (int j = v2 + 1; j < vertexList.size(); j++) {
if (edges[v1][j] > 0) {
return j;
}
}
return -1;
}
// 深度优先遍历算法
// i 第一次就是 0
private void dfs(boolean[] isVisited, int i) {
// 首先我们访问该结点,输出
System.out.print(getValueByIndex(i) + "->");
// 将结点设置为已经访问
isVisited[i] = true;
// 查找结点i的第一个邻接结点w
int w = getFirstNeighbor(i);
while (w != -1) {// 说明有
if (!isVisited[w]) {
dfs(isVisited, w);
}
// 如果w结点已经被访问过
w = getNextNeighbor(i, w);
}
}
// 对dfs 进行一个重载, 遍历我们所有的结点,并进行 dfs
public void dfs() {
boolean[] isVisited = new boolean[vertexList.size()];
// 遍历所有的结点,进行dfs[回溯]
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
dfs(isVisited, i);
}
}
}
// 对一个结点进行广度优先遍历的方法
private void bfs(boolean[] isVisited, int i) {
int u; // 表示队列的头结点对应下标
int w; // 邻接结点w
// 队列,记录结点访问的顺序
LinkedList<Integer> queue = new LinkedList<Integer>();
// 访问结点,输出结点信息
System.out.print(getValueByIndex(i) + "=>");
// 标记为已访问
isVisited[i] = true;
// 将结点加入队列
queue.addLast(i);
while (!queue.isEmpty()) {// 体现出我们的广度优先
// 取出队列的头结点下标
u = queue.removeFirst();
// 得到第一个邻接结点的下标 w
w = getFirstNeighbor(u);
while (w != -1) {// 找到
// 是否访问过
if (!isVisited[w]) {
System.out.print(getValueByIndex(w) + "=>");
// 标记已经访问
isVisited[w] = true;
// 入队
queue.addLast(w);
}
// 以u为前驱点,找w后面的下一个邻结点
w = getNextNeighbor(u, w);
}
}
}
// 遍历所有的结点,都进行广度优先搜索
public void bfs() {
boolean[] isVisited = new boolean[vertexList.size()];
for (int i = 0; i < getNumOfVertex(); i++) {
if (!isVisited[i]) {
bfs(isVisited, i);
}
}
}
}# 程序员常用 10 种算法
# 1、二分查找算法
# 1.1、二分查找算法介绍
- 前面我们讲过了二分查找算法,是使用递归的方式,下面我们讲解二分查找算法的非递归方式
- 二分查找法只适用于从有序的数列中进行查找 (比如数字和字母等),将数列排序后再进行查找
- 二分查找法的运行时间为对数时间 O (log2n) ,即查找到需要的目标位置最多只需要 log2n 步,假设从 [0,99] 的队列 (100 个数,即 n=100) 中寻到目标数 30,则需要查找步数为 log2100 , 即最多需要查找 7 次 ( 2^6 < 100 < 2^7)
# 1.2、二分查找算法思路
- 二分查找需要将数组分为两个部分:左边和右边,所以需要三个指针来记录位置
- left :数组左边界,初始值为 0
- right :数组右边界,初始值为 arr.length - 1
- mid :数组中间值指针,mid = (left + right) / 2
- 目标值 value 与 mid 所指向的值相比较
- value == arr [mid] :找到,返回
- value <arr [mid] :目标值在数组左边,下次需要在 left~(mid-1) 内搜索
- value > arr [mid] :目标值在数组右边,下次需要在 (mid+1))~(right) 内搜索
- 何时停止?left > right 时,表示没有找到,返回索引 -1
# 1.3、二分查找算法实现
- 代码实现
public class BinarySearchNoRecur {
public static void main(String[] args) {
// 测试
int[] arr = { 1, 3, 8, 10, 11, 67, 100 };
int index = binarySearch(arr, 100);
System.out.println("index=" + index);
}
// 二分查找的非递归实现
/**
*
* @param arr 待查找的数组, arr是升序排序
* @param target 需要查找的数
* @return 返回对应下标,-1表示没有找到
*/
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) { // 说明继续查找
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] > target) {
right = mid - 1;// 需要向左边查找
} else {
left = mid + 1; // 需要向右边查找
}
}
return -1;
}
}- 程序运行结果
index=6# 2、分治算法
# 2.1、分治算法介绍
- 分治法是一种很重要的算法。字面上的解释是 “分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题…… 直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法 (快速排序,归并排序),傅立叶变换 (快速傅立叶变换)……
- 分治算法可以求解的一些经典问题
- 二分搜索
- 大整数乘法
- 棋盘覆盖
- 合并排序
- 快速排序
- 线性时间选择
- 最接近点对问题
- 循环赛日程表
- 汉诺塔
# 2.2、分治算法基本步骤
- 分治法在每一层递归上都有三个步骤:
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题
- 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
- 合并:将各个子问题的解合并为原问题的解。
# 2.3、分治算法设计模式
- 其中 | P | 表示问题 P 的规模;n0 为一阈值,表示当问题 P 的规模不超过 n0 时,问题已容易直接解出,不必再继续分解。
- ADHOC§ 是该分治法中的基本子算法,用于直接解小规模的问题 P。
- 因此,当 P 的规模不超过 n0 时直接用算法 ADHOC§ 求解。
- 算法 MERGE (y1,y2,…,yk) 是该分治法中的合并子算法,用于将 P 的子问题 P1 ,P2 ,…,Pk 的相应的解 y1,y2,…,yk 合并为 P 的解
if |P|≤n0
then return(ADHOC(P))
//将P分解为较小的子问题 P1 ,P2 ,…,Pk
for i←1 to k
do yi ← Divide-and-Conquer(Pi) // 递归解决Pi
T ← MERGE(y1,y2,…,yk) // 合并子问题
return(T)# 2.4、汉诺塔问题
# 2.4.1、汉诺塔介绍
- 汉诺塔的传说:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
- 假如每秒钟一次,共需多长时间呢?移完这些金片需要 5845.54 亿年以上,太阳系的预期寿命据说也就是数百亿年。真的过了 5845.54 亿年,地球上的一切生命,连同梵塔、庙宇等,都早已经灰飞烟灭。
# 2.4.2、分治思路
- 如果 A 塔上只有一个盘子:
- 直接将 A 塔的盘子移动到 C 塔:A —> C
- 如果 A 塔上有两个盘子:
- 先将 A 塔上面的盘子移动到 B 塔:A —> B
- 再将 A 塔最下面的盘子移动到 C 塔:A --> C
- 最后将 B 塔上面的盘子移动到 C 塔:B --> C
- 如果 A 塔上有三个盘子:
- n >= 2 时,就体现出了分治算法的思想:我们将 A 塔上面的盘子看作一个整体,最下面的单个盘子单独分离出来,分三步走
- 先将 A 塔上面的盘子看作一个整体,移动到 B 塔(把 C 塔当做中转站)
- 这样 A 塔就只剩下一个最大的盘子,将 A 塔剩下的盘子移动到 C 塔
- 最后将 B 塔上面的盘子移动到 C 塔(把 A 塔当做中转站)
# 2.4.3、代码实现
- 解决汉诺塔问题:
public class Hanoitower {
public static void main(String[] args) {
hanoiTower(3, 'A', 'B', 'C');
}
//汉诺塔的移动的方法
//使用分治算法
public static void hanoiTower(int num, char a, char b, char c) {
//如果只有一个盘
if(num == 1) {
System.out.println("第1个盘从 " + a + "->" + c);
} else {
//如果我们有 n >= 2 情况,我们总是可以看做是两个盘 1.最下边的一个盘 2. 上面的所有盘
//1. 先把 最上面的所有盘 A->B, 移动过程会使用到 c
hanoiTower(num - 1, a, c, b);
//2. 把最下边的盘 A->C
System.out.println("第" + num + "个盘从 " + a + "->" + c);
//3. 把B塔的所有盘 从 B->C , 移动过程使用到 a塔
hanoiTower(num - 1, b, a, c);
}
}
}- 程序运行结果
第1个盘从 A->C
第2个盘从 A->B
第1个盘从 C->B
第3个盘从 A->C
第1个盘从 B->A
第2个盘从 B->C
第1个盘从 A->C# 3、动态规划算法
# 3.1、应用场景
- 背包问题:有一个背包,容量为 4 磅 , 现有如下物品
- 要求达到的目标为装入的背包的总价值最大,并且重量不超出
- 要求装入的物品不能重复
| 物品 | 重量 | 价格 |
|---|---|---|
| 吉他 (G) | 1 | 1500 |
| 音响 (S) | 4 | 3000 |
| 电脑 (L) | 3 | 2000 |
# 3.2、动态规划算法介绍
- 动态规划 (Dynamic Programming) 算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
- 动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
- 与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 )
- 动态规划可以通过填表的方式来逐步推进,得到最优解
# 3.3、背包问题
# 3.3.1、背包问题介绍
- 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品,如何选择物品放入背包使物品的价值最大。其中又分 01 背包和完全背包 (完全背包指的是:每种物品都有无限件可用)
- 这里的问题属于 01 背包,即每个物品最多放一个。而无限背包可以转化为 01 背包。
# 3.3.2、代码思路
- 背包容量为 4 磅,物品价格以及重量表如下:
| 物品 | 重量 | 价格 |
|---|---|---|
| 吉他 (G) | 1 | 1500 |
| 音响 (S) | 4 | 3000 |
| 电脑 (L) | 3 | 2000 |
- 先来填表 v ,对应着数组
v[][],我来解释下这张表:- 算法的主要思想:利用动态规划来解决。
- 每次遍历到的第 i 个物品,根据 w [i - 1](物品重量)和 val [i - 1](物品价值)来确定是否需要将该物品放入背包中,C 为背包的容量
v[i][j]表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值
| 物品 | 0 磅 | 1 磅 | 2 磅 | 3 磅 | 4 磅 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 吉他 (G) | 0 | ||||
| 音响 (S) | 0 | ||||
| 电脑 (L) | 0 |
- 对于第一行 (i=1),目前只有吉他可以选择,这时不管背包容量多大,也只能放一把吉他
| 物品 | 0 磅 | 1**** 磅 | 2**** 磅 | 3**** 磅 | 4**** 磅 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 吉他 (G) | 0 | 1500(G) | 1500(G) | 1500(G) | 1500(G) |
| 音响 (S) | 0 | ||||
| 电脑 (L) | 0 |
- 对于第二行 (i=2),目前存在吉他和音响可以选择,新物品为音响,重量为 4 磅,尝试将其放入背包
- 在
v[2][4]单元格,尝试将音响放入容量为 4 磅的背包中,看看背包还剩多少容量?还剩 0 磅,再去找找 0 磅能放入最大价值多高的物品:v[1][0] = 0 - 与上一次
v[1][4]比较 ,v[1][4] < v[2][4],发现确实比之前放得多,采取此方案
- 在
| 物品 | 0 磅 | 1**** 磅 | 2**** 磅 | 3**** 磅 | 4**** 磅 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 吉他 (G) | 0 | 1500(G) | 1500(G) | 1500(G) | 1500(G) |
| 音响 (S) | 0 | 1500(G) | 1500(G) | 1500(G) | 3000(S) |
| 电脑 (L) | 0 |
- 对于第三行 (i=3),目前存在吉他和音响、电脑可以选择,新物品为电脑,重量为 3 磅,尝试将其放入背包
- 当背包容量为 3 磅时,可以放入电脑
- 在
v[3][3]单元格,尝试将电脑放入容量为 3 磅的背包中,看看背包还剩多少容量?还剩 0 磅,再去找找 0 磅能放入最大价值多高的物品:v[2][0] = 0 - 与上一次
v[2][3]比较 ,v[2][3] < v[3][3],发现确实比之前放得多,采取此方案
- 在
- 当背包容量为 4 磅时,可以放入电脑
- 在
v[3][4]单元格,尝试将电脑放入容量为 4 磅的背包中,看看背包还剩多少容量?还剩 1 磅,再去找找 1 磅能放入最大价值多高的物品:v[2][1] = 1500,所以总共能放入的重量为v[3][4] = 3500 - 与上一次
v[2][4]比较 ,v[2][4] < v[3][4],发现确实比之前放得多,采取此方案
- 在
- 当背包容量为 3 磅时,可以放入电脑
| 物品 | 0 磅 | 1**** 磅 | 2**** 磅 | 3**** 磅 | 4**** 磅 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 吉他 (G) | 0 | 1500(G) | 1500(G) | 1500(G) | 1500(G) |
| 音响 (S) | 0 | 1500(G) | 1500(G) | 1500(G) | 3000(S) |
| 电脑 (L) | 0 | 1500(G) | 1500(G) | 2000(L) | 3500(L+G) |
-
总结公式:
- 当前新增物品的重量 > 背包的重量,则直接拷贝上次的方案
if (w[i - 1] > j) { // 因为我们程序i 是从1开始的,所以是 w[i-1] v[i][j] = v[i - 1][j]; }- 当前新增物品的重量 <= 背包的重量
- 尝试将新物品放入背包,看看还剩多少容量
- 尝试剩余的容量填满,看看此时背包里物品的价值和上次比,哪个更大,取价格更大的方案即可
if (w[i - 1] <= j) { // 因为我们程序i 是从1开始的,所以是 w[i-1] v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]); } -
为什么可以这样做?将大问题拆成小问题
- 第一步:求得第一步步骤的最优解
- 第二步:求得第二步步骤的最优解,第二步的最优解依赖于第一步的最优解
- …
- 第 n 步:求得第 n 步步骤的最优解,第 n 步的最优解依赖于第 n-1 步的最优解
# 3.3.3、代码实现
- 背包问题算法
public class KnapsackProblem {
public static void main(String[] args) {
int[] w = { 1, 4, 3 };// 物品的重量
int[] val = { 1500, 3000, 2000 }; // 物品的价值 这里val[i]
int m = 4; // 背包的容量
int n = val.length; // 物品的个数
// 创建二维数组,
// v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值
int[][] v = new int[n + 1][m + 1];
// 为了记录放入商品的情况,我们定一个二维数组
int[][] path = new int[n + 1][m + 1];
// 初始化第一行和第一列, 这里在本程序中,可以不去处理,因为默认就是0
for (int i = 0; i < v.length; i++) {
v[i][0] = 0; // 将第一列设置为0
}
for (int i = 0; i < v[0].length; i++) {
v[0][i] = 0; // 将第一行设置0
}
// 根据前面得到公式来动态规划处理
for (int i = 1; i < v.length; i++) { // 不处理第一行 i是从1开始的
for (int j = 1; j < v[0].length; j++) {// 不处理第一列, j是从1开始的
// 公式
if (w[i - 1] > j) { // 因为我们程序i 是从1开始的,所以是 w[i-1]
v[i][j] = v[i - 1][j];
} else {
// 说明:
// 因为我们的i 从1开始的, 因此公式需要调整成
// v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]);
// 为了记录商品存放到背包的情况,我们不能直接的使用上面的公式,需要使用if-else来体现公式
if (v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) {
v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
// 把当前的情况记录到path
path[i][j] = 1;
} else {
v[i][j] = v[i - 1][j];
}
}
}
}
// 输出一下v 看看目前的情况
for (int i = 0; i < v.length; i++) {
for (int j = 0; j < v[i].length; j++) {
System.out.print(v[i][j] + "\t ");
}
System.out.println();
}
System.out.println("============================");
// 动脑筋
int i = path.length - 1; // 行的最大下标
int j = path[0].length - 1; // 列的最大下标
while (i > 0 && j > 0) { // 从path的最后开始找
if (path[i][j] == 1) {
System.out.printf("第%d个商品放入到背包\n", i);
j -= w[i - 1]; // w[i-1]
}
i--;
}
}
}- 程序运行结果
0 0 0 0 0
0 1500 1500 1500 1500
0 1500 1500 1500 3000
0 1500 1500 2000 3500
============================
第3个商品放入到背包
第1个商品放入到背包# 3.4、爬楼梯问题
# 3.4.1、代码思路
- 当 n < 0 时,无解
- 当 n = 1 时,f (n) = 1
- 当 n = 2 时,有两种方法:
- 走两次一级楼梯
- 一下走两级楼梯
- 当 n > 2 时,设总共的跳法为 f (n) 中,第一次跳一级还是两级,决定了后面剩下的台阶的跳法数目的不同:
- 如果第一次只跳一级,则后面剩下的 n-1 级台阶的跳法数目为 f (n-1)
- 如果第一次跳两级,则后面剩下的 n-2 级台阶的跳法数目为 f (n-2)
- 所以,得出递归方程,f (n) = f (n-1) + f (n-2),问题本质是斐波那契数列。
# 3.4.2、代码实现
/**上台阶问题,dp**/
public static int climbStairs(int n) {
if(n==0) return -1;
if(n==1) return 1;
int []dp = new int [n];
dp[0] =1;
dp[1] =2;
for(int i=0;i<n-2;i++) {
dp[i+2]=dp[i]+dp[i+1];
}
return dp[n-1];
}# 4、KMP 算法
# 4.1、应用场景
- 字符串匹配问题:
- 有一个字符串 str1= ““硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好””,和一个子串 str2=“尚硅谷你尚硅你”
- 现在要判断 str1 是否含有 str2,如果存在,就返回第一次出现的位置,如果没有,则返回 - 1
# 4.2、暴力匹配算法
# 4.2.1、暴力匹配代码思路
- 如果用暴力匹配的思路,需要两个指针:i ,j ,i 表示现在 str1 匹配到索引为 i 的位置,子串 str2 匹配到索引为 j 的位置
- 如果当前字符匹配成功(即 str1 [i] == str2 [j]),则 i++,j++,继续匹配下一个字符
- 如果失配(即 str1 [i]! = str2 [j]),令 i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯,j 被置为 0
- 用暴力方法解决的话就会有大量的回溯,每次只移动一位,若是不匹配,移动到下一位接着判断,浪费了大量的时间。(不可行!)
- 为什么匹配失败后,要令指针 i 回溯匹配起始位置的下一个位置?就比如说 001112 和 112 ,当 i 扫描至 str1 [4] ,j 扫描至 str2 [4] 时,发现字符串不匹配。i 重新回到 str1 [2] 的下一个位置 str1 [3] ,继续执行扫描,str1 [3~5] 和 str2 [0~2] 相等,匹配成功
# 4.2.2、暴力匹配代码
- 代码
public class ViolenceMatch {
public static void main(String[] args) {
// TODO Auto-generated method stub
// 测试暴力匹配算法
String str1 = "硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好";
String str2 = "尚硅谷你尚硅你";
int index = violenceMatch(str1, str2);
System.out.println("index=" + index);
}
// 暴力匹配算法实现
public static int violenceMatch(String str1, String str2) {
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int s1Len = s1.length;
int s2Len = s2.length;
int i = 0; // i索引指向s1
int j = 0; // j索引指向s2
while (i < s1Len && j < s2Len) {// 保证匹配时,不越界
if (s1[i] == s2[j]) {// 匹配ok
i++;
j++;
} else { // 没有匹配成功
// 如果失配(即str1[i]! = str2[j]),令i = i - (j - 1),j = 0。
i = i - (j - 1);
j = 0;
}
}
// 判断是否匹配成功
if (j == s2Len) {
return i - j;
} else {
return -1;
}
}
}- 程序运行结果
index=15# 4.3、KMP 算法
# 4.3.1、KMP 算法介绍
- KMP 是一个解决模式串在文本串是否出现过,如果出现过,最早出现的位置的经典算法
- Knuth-Morris-Pratt 字符串查找算法,简称为 “KMP 算法”,常用于在一个文本串 S 内查找一个模式串 P 的出现位置,这个算法由 Donald Knuth、Vaughan Pratt、James H. Morris 三人于 1977 年联合发表,故取这 3 人的姓氏命名此算法.
- KMP 方法算法利用之前判断过信息,通过一个 next 数组,保存模式串中前后最长公共子序列的长度,每次回溯时,通过 next 数组找到,前面匹配过的位置,省去了大量的计算时间
- 参考资料:https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html
# 4.3.2、KMP 算法流程
- 举例来说,有一个字符串 Str1 = “BBC ABCDAB ABCDABCDABDE”,判断,里面是否包含另一个字符串 Str2 = “ABCDABD”?
- 首先,第一步用 Str1 的第一个字符和 Str2 的第一个字符去比较,不符合,关键词向后移动一位
- 重复第一步,还是不符合,再后移
- 一直重复,直到 Str1 有一个字符与 Str2 的第一个字符符合为止
- 接着比较字符串和搜索词的下一个字符,还是符合
- 遇到 Str1 有一个字符与 Str2 对应的字符不符合
- 这时候,想到的是继续遍历 Str1 的下一个字符,重复第 1 步
- 其实是很不明智的,因为此时 BCD 已经比较过了,没有必要再做重复的工作,一个基本事实是,当空格与 D 不匹配时,你其实知道前面六个字符是”ABCDAB”
- 为什么我知道 BCD 已经比较过了呢?待匹配的子串为 ABCDABD ,当在源字符串中匹配至 ABCDABX(X != D) 时, BCD 很明显不可能与字符串 A 匹配成功,但 ABX 有可能与 ABC 相等,所以 ABXXXXX 有可能与 ADCDABD 匹配成功,所以我们直接将搜索位置向后移动 4 个位置
- KMP 算法的想法是,设法利用这个已知信息,不要把搜索位置移回已经比较过的位置,继续把它向后移,这样就提高了效率
- 怎么做到把刚刚重复的步骤省略掉?可以对 Str2 计算出一张《部分匹配表》,这张表的产生在后面介绍
-
已知空格与 D 不匹配时,前面六个字符”ABCDAB” 是匹配的。查表可知,最后一个匹配字符 B 对应的” 部分匹配值” 为 2,因此按照下面的公式算出向后移动的位数:
-
移动位数 = 已匹配的字符数 - 对应的部分匹配值
-
因为 6 - 2 等于 4,所以将搜索词向后移动 4 位。
-
说白了,不就是字符串 ABCDAB 的后缀中包含 AB ,前缀也包含了 AB
-
当我们匹配到了 ABCDABX(X != D) 时,其实 BCD 部分其实无须再去匹配,但因为后缀 ABX 有可能等于 ABC ,所以需要从 ABX 中的 A 开始匹配,
-
相同的前后缀 AB 长度为 2 ,所以搜索位置向后移动 4 位(待匹配的子串长度 - 相同的前后缀长度)
-
-
- 因为空格与C不匹配,搜索词还要继续往后移。
- 这时,已匹配的字符数为 2(”AB”),对应的” 部分匹配值” 为 0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移 2 位。
- 来仔细想想,为啥是向后移动 2 位?
- 当我们匹配到 ABX(X != C)时,我们需要考虑搜索位置往后面移动多少个位置
- 由于字符串 AB 没有相同的前后缀,所以部分匹配值为 0 ,也就是说,如果匹配不到子串 匹配到 ABX(X != C) ,直接从 X 的位置开始继续搜索,因为字符串 AB 中没有相同的前后缀~~~
- 因为空格与 A 不匹配,继续后移一位
- 逐位比较,直到发现 C 与 D 不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动 4 位
- 逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动 7 位,这里就不再重复了
# 4.3.3、部分匹配表
- 有没有想过部分匹配表怎么产生的?首先我们先介绍字符串的前缀,后缀是什么?
-
“部分匹配值” 就是” 前缀” 和” 后缀” 的最长的共有元素的长度。以”ABCDABD” 为例,
- ”A” 的前缀和后缀都为空集,共有元素的长度为 0;
- ”AB” 的前缀为 [A],后缀为 [B],共有元素的长度为 0;
- ”ABC” 的前缀为 [A, AB],后缀为 [BC, C],共有元素的长度 0;
- ”ABCD” 的前缀为 [A, AB, ABC],后缀为 [BCD, CD, D],共有元素的长度为 0;
- ”ABCDA” 的前缀为 [A, AB, ABC, ABCD],后缀为 [BCDA, CDA, DA, A],共有元素为”A”,长度为 1;
- ”ABCDAB” 的前缀为 [A, AB, ABC, ABCD, ABCDA],后缀为 [BCDAB, CDAB, DAB, AB, B],共有元素为”AB”,长度为 2;
- ”ABCDABD” 的前缀为 [A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为 [BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为 0。
- 计算部分匹配表时,当前字符串的部分匹配表的求解依赖于上个子串的部分匹配表
-
” 部分匹配” 的实质是,有时候,字符串头部和尾部会有重复。比如,”ABCDAB” 之中有两个”AB”,那么它的” 部分匹配值” 就是 2(”AB” 的长度)。搜索词移动的时候,第一个”AB” 向后移动 4 位(字符串长度 - 部分匹配值),就可以来到第二个”AB” 的位置。
# 4.3.4、KMP 算法实现
# 1、计算部分匹配表
- KMP 中的关键就是求公共最长匹配前缀和后缀的长度了(多读几遍这句话,你就懂了)
- next 数组的含义:next [i] 表示原字符串的子串 str.subString (0, i) 中,前缀和后缀的最长的共有元素的长度
- 首先,如果只包含单个字符的字符串,其部分匹配表为 {0} ,所以 next [0] = 0;
- 然后索引 i 从 1 ~ dest.length () 递增,依次求取每个子串的部分匹配表,就很神奇,下一次子串的部分匹配表的求解依赖于上一次子串的部分匹配表(具体看下面)
- 索引 j 的含义:
- 索引 j 指向当前待匹配字符的索引,每当匹配到一个字符时,索引 j 便执行 +1 操作
- 比如匹配 ABCDA 时,i 指向最后一个 A ,即 i == 4 ,此时 j 还是 0 ,匹配到 str [i] == str [j] ,j +=1 ,为下一次匹配做准备
- 怎么求每个子串的部分匹配值呢?以 ABCDABD 为例
- A 的部分匹配表为 {0} ,那么 AB、ABC、ABCD、ABCDA、ABCDAB、ABCDABD 的部分匹配表要怎么计算呢?其实每个字符串的部分匹配表都要根据上一个子串的部分匹配表来计算
- 比如我们需要求 ABCDAB 的部分匹配表
- 我们在上一步已经求出 ABCDA 的部分匹配表为
- 此时 i == 5 ,j == 1 ,我们尝试匹配 str [j] 和 str [i] :str [j] == str [i] == ‘B’ ,匹配成功,我们在上一步部分匹配表的基础上,对最后一个部分匹配值进行 +1 操作
- 所以我们求得 ABCDAB 的部分匹配表为
- 再来,我们现在继续求 ABCDABD 的部分匹配表
- 我们在上一步已经求出 ABCDAB 的部分匹配表为
- 此时 i == 6 ,j == 2 ,我们尝试匹配 str [j] 和 str [i] :str [j] == ‘C’ , str [i] == ‘D’ ,发现 str [j] != str [i]
- 我们进行匹配,发现 “ABC” != “ABD” 时,j 就应该进行回退,索引 j 肯定需要往前面回溯,那么 j 怎么回溯呢?
- 举个例子:“ABCX” 和 “ABDX” ,其中 X 为任意字符,因为有字符 D 的存在,如果想要前缀与后缀匹配,只能再从头开始算起,所以 j 需要回退到 ABC 中的 A 字符,即 j = next [j - 1];
// 获取到一个字符串(子串) 的部分匹配表
public static int[] kmpNext(String dest) {
// 创建一个next 数组保存部分匹配值
int[] next = new int[dest.length()];
next[0] = 0; // 如果字符串是长度为1 部分匹配值就是0
for (int i = 1, j = 0; i < dest.length(); i++) {
// 当dest.charAt(i) != dest.charAt(j) ,我们需要从next[j-1]获取新的j
// 直到我们发现 有 dest.charAt(i) == dest.charAt(j)成立才退出
// 这是kmp算法的核心点
while (j > 0 && dest.charAt(i) != dest.charAt(j)) {
j = next[j - 1];
}
// 当dest.charAt(i) == dest.charAt(j) 满足时,部分匹配值就是+1
if (dest.charAt(i) == dest.charAt(j)) {
j++;
}
next[i] = j;
}
return next;
}看到一篇写 KMP 的博客,写得还不错
参考资料:https://blog.csdn.net/dark_cy/article/details/88698736
# 2、执行 KMP 搜索
-
索引 i 从 0 ~ dest.length () 递增,依次与目标子串中的字符进行比较
-
next [] 为部分搜索表
-
如果当前字符匹配成功,则 j++ ,为匹配下一个字符做准备
-
如果当前字符匹配失败,则 j 往前回溯,具体做法是:从子串的部分匹配表中,获取当前需要从子串的哪个索引位置开始继续执行匹配(j = next[j - 1]),目的是为了跳过那些没有必要再比较的字符
// 写出我们的kmp搜索算法
/**
*
* @param str1 源字符串
* @param str2 子串
* @param next 部分匹配表, 是子串对应的部分匹配表
* @return 如果是-1就是没有匹配到,否则返回第一个匹配的位置
*/
public static int kmpSearch(String str1, String str2, int[] next) {
// 遍历
for (int i = 0, j = 0; i < str1.length(); i++) {
// 需要处理 str1.charAt(i) != str2.charAt(j), 去调整j的大小
// KMP算法核心点, 可以验证...
while (j > 0 && str1.charAt(i) != str2.charAt(j)) {
j = next[j - 1];
}
if (str1.charAt(i) == str2.charAt(j)) {
j++;
}
if (j == str2.length()) { // 找到了
return i - j + 1;
}
}
return -1;
}# 3、代码测试
- 首先计算待搜索子串的部分匹配表
- 然后从利用子串的部分匹配表,在源字符串中进行搜索
public static void main(String[] args) {
String str1 = "BBC ABCDAB ABCDABCDABDE";
String str2 = "ABCDABD";
// String str2 = "BBC";
int[] next = kmpNext("ABCDABD"); // [0, 1, 2, 0]
System.out.println("next=" + Arrays.toString(next));
int index = kmpSearch(str1, str2, next);
System.out.println("index=" + index); // 15
}- 程序运行结果
next=[0, 0, 0, 0, 1, 2, 0]
index=15# 5、贪心算法
# 5.1、应用场景 (集合覆盖问题)
- 假设存在下面需要付费的广播台,以及广播台信号可以覆盖的地区。 如何选择最少的广播台,让所有的地区都可以接收到信号
| 广播台 | 覆盖地区 |
|---|---|
| K1 | “北京”, “上海”, “天津” |
| K2 | “广州”, “北京”, “深圳” |
| K3 | “成都”, “上海”, “杭州” |
| K4 | “上海”, “天津” |
| K5 | “杭州”, “大连” |
# 5.2、贪心算法介绍
- 贪婪算法 (贪心算法) 是指在对问题进行求解时,在每一步选择中都采取最好或者最优 (即最有利) 的选择,从而希望能够导致结果是最好或者最优的算法
- 贪婪算法所得到的结果不一定是最优的结果 (有时候会是最优解),但是都是相对近似 (接近) 最优解的结果
# 5.3、集合覆盖问题
# 5.3.1、穷举法缺点
- 如何找出覆盖所有地区的广播台的集合呢,使用穷举法实现,列出每个可能的广播台的集合,这被称为幂集。假设总的有 n 个广播台,则广播台的组合总共有 2ⁿ -1 个,假设每秒可以计算 10 个子集,
| 广播台数量 n | 子集总数 2ⁿ | 需要的时间 |
|---|---|---|
| 5 | 32 | 3.2 秒 |
| 10 | 1024 | 102.4 秒 |
| 32 | 4294967296 | 13.6 年 |
| 100 | 1.26*100³º | 4x10²³ 年 |
# 5.3.2、代码思路
- 目前并没有算法可以快速计算得到准备的值, 使用贪婪算法,则可以得到非常接近的解,并且效率高
- 在选择策略上,因为需要覆盖全部地区的最小集合,大致思路如下:
- 声明几个辅助变量:
ArrayList<String> selects;:存放已经选取的电台,比如HashSet<String> allAreas;:存放当前还未覆盖的地区String maxKey = null;:存放当前能覆盖最多未覆盖地区的电台,比如 K1、K2
- 在所有电台中,找到一个能覆盖最多还未覆盖地区的电台(此电台可能包含一些已覆盖的地区,但没有关系):maxKey
- 将其加入到 selects 集合中,表示已经选了该电台
- 将 maxKey 电台中的地区从 allAreas 中移除
- 重复如上步骤,直至 allAreas 为空
- 声明几个辅助变量:
# 5.3.3、代码实现
- 使用贪心算法解决集合覆盖问题
public class GreedyAlgorithm {
public static void main(String[] args) {
// 创建广播电台,放入到Map
HashMap<String, HashSet<String>> broadcasts = new HashMap<String, HashSet<String>>();
// 将各个电台放入到broadcasts
HashSet<String> hashSet1 = new HashSet<String>();
hashSet1.add("北京");
hashSet1.add("上海");
hashSet1.add("天津");
HashSet<String> hashSet2 = new HashSet<String>();
hashSet2.add("广州");
hashSet2.add("北京");
hashSet2.add("深圳");
HashSet<String> hashSet3 = new HashSet<String>();
hashSet3.add("成都");
hashSet3.add("上海");
hashSet3.add("杭州");
HashSet<String> hashSet4 = new HashSet<String>();
hashSet4.add("上海");
hashSet4.add("天津");
HashSet<String> hashSet5 = new HashSet<String>();
hashSet5.add("杭州");
hashSet5.add("大连");
// 加入到map
broadcasts.put("K1", hashSet1);
broadcasts.put("K2", hashSet2);
broadcasts.put("K3", hashSet3);
broadcasts.put("K4", hashSet4);
broadcasts.put("K5", hashSet5);
// allAreas 存放所有的地区
HashSet<String> allAreas = new HashSet<String>();
for (Entry<String, HashSet<String>> broadcast : broadcasts.entrySet()) {
allAreas.addAll(broadcast.getValue());
}
// 创建ArrayList, 存放选择的电台集合
ArrayList<String> selects = new ArrayList<String>();
// 定义一个临时的集合, 在遍历的过程中,存放遍历过程中的电台覆盖的地区和当前还没有覆盖地区的交集
HashSet<String> tempSet = new HashSet<String>();
// 定义给maxKey , 保存在一次遍历过程中,能够覆盖最大未覆盖的地区对应的电台的key
// 如果maxKey 不为null , 则会加入到 selects
String maxKey = null;
Integer maxCount = 0;
Integer curCount = 0;
while (allAreas.size() != 0) { // 如果allAreas 不为0, 则表示还没有覆盖到所有的地区
// 每进行一次while,需要重置指针,重置计数器
maxKey = null;
maxCount = 0;
// 遍历 broadcasts, 取出对应key
for (String key : broadcasts.keySet()) {
// 每进行一次for清除tempSet
tempSet.clear();
// 当前这个key能够覆盖的地区
HashSet<String> areas = broadcasts.get(key);
tempSet.addAll(areas);
// 求出tempSet 和 allAreas 集合的交集, 交集会赋给 tempSet
tempSet.retainAll(allAreas);
// 当前站台可以覆盖额外的多少个城市
curCount = tempSet.size();
// 如果当前这个集合包含的未覆盖地区的数量,比maxKey指向的集合地区还多,就需要重置maxKey
// curCount > maxCount 体现出贪心算法的特点,每次都选择最优的
if (curCount > maxCount) {
maxKey = key;
maxCount = curCount;
}
}
// maxKey != null, 就应该将maxKey 加入selects
if (maxKey != null) {
selects.add(maxKey);
// 将maxKey指向的广播电台覆盖的地区,从 allAreas 去掉
allAreas.removeAll(broadcasts.get(maxKey));
}
}
System.out.println("得到的选择结果是" + selects);// [K1,K2,K3,K5]
}
}- 程序运行结果
得到的选择结果是[K1, K2, K3, K5]# 5.4、注意事项
- 贪婪算法所得到的结果不一定是最优的结果 (有时候会是最优解),但是都是相对近似 (接近) 最优解的结果
- 比如上题的算法选出的是 K1, K2, K3, K5,符合覆盖了全部的地区
- 但是我们发现 K2, K3,K4,K5 也可以覆盖全部地区,如果 K2 的使用成本低于 K1, 那么我们上题的 K1, K2, K3, K5 虽然是满足条件,但是并不是最优的
# 6、普里姆算法
# 6.1、应用场景 (修路问题)
- 看一个应用场景和问题:
- 有胜利乡有 7 个村庄 (A, B, C, D, E, F, G) ,现在需要修路把 7 个村庄连通
- 各个村庄的距离用边线表示 (权) ,比如 A – B 距离 5 公里
- 问:如何修路保证各个村庄都能连通,并且总的修建公路总里程最短?
- 正确的思路,就是尽可能的选择少的路线,并且每条路线最小,保证总里程数最少
# 6.2、最小生成树
- 修路问题本质就是就是最小生成树问题, 先介绍一下最小生成树 (Minimum Cost Spanning Tree),简称 MST。
- 给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树
- N 个顶点,一定有 N-1 条边
- 包含全部顶点
- N-1 条边都在图中
- 求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法
# 6.3、普里姆算法介绍
- 普利姆 (Prim) 算法求最小生成树,也就是在包含 n 个顶点的连通图中,找出只有 (n-1) 条边包含所有 n 个顶点的连通子图,也就是所谓的极小连通子图
- 普利姆的算法如下:
- 设 G=(V,E) 是连通网,T=(U,D) 是最小生成树,V,U 是顶点集合,E,D 是边的集合
- 若从顶点 u 开始构造最小生成树,则从集合 V 中取出顶点 u 放入集合 U 中,标记顶点 v 的 visited [u]=1
- 若集合 U 中顶点 ui 与集合 V-U 中的顶点 vj 之间存在边,则寻找这些边中权值最小的边,但不能构成回路,将顶点 vj 加入集合 U 中,将边(ui,vj)加入集合 D 中,标记 visited [vj]=1
- 重复上述步骤,直到 U 与 V 相等,即所有顶点都被标记为访问过,此时 D 中有 n-1 条边
- 提示:单独看步骤很难理解,我们通过实例和代码来讲解,比较好理解
# 6.4、代码思路
- 举例来说明,就用下面这张图,起始顶点起始无所谓,因为顶点有 7 个,边数最少为 6 条边,最后得到的 6 条边中,其路径长度都是所有边中路径长度最短的
- 第一步:选取顶点 A ,并标记顶点 A 已被访问,求取最短路径
- A – > B :路径长度为 5
- A – > C :路径长度为 7
- A – > G :路径长度为 2
- 选取最短路径 <A, G> ,其长度为 2
- 标记顶点 G 已被访问过
- 第二步:同样也是求取最短路径
- A – > B :路径长度为 5
- A – > C :路径长度为 7
- A – > G :G 已经被访问过,不考虑
- G – > B :路径长度为 3
- G – > E :路径长度为 4
- G – > F :路径长度为 6
- 选取最短路径 <G, B> ,其长度为 3
- 标记顶点 B 已被访问过
- 第三步:同样也是求取最短路径
- A – > B :B 已经被访问过,不考虑
- A – > C :路径长度为 7
- A – > G :G 已经被访问过,不考虑
- G – > B :B 已经被访问过,不考虑
- G – > E :路径长度为 4
- G – > F :路径长度为 6
- B --> A :A 已经被访问过,不考虑
- B --> D :路径长度为 9
- 选取最短路径 <G, E> ,其长度为 4
- 标记顶点 E 已被访问过
- 第 n 步:以此类推
- 什么时候停止?n 个顶点最少需要 n - 1 条边
- 我感觉我可以优化上面的逻辑和下面的代码,改日吧
# 6.5、代码实现
# 6.5.1、图的定义
- 使用邻接矩阵法,定义一张图
class MGraph {
int verxs; // 表示图的节点个数
char[] data;// 存放结点数据
int[][] weight; // 存放边,就是我们的邻接矩阵
public MGraph(int verxs) {
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
//创建图的邻接矩阵
/**
*
* @param graph 图对象
* @param verxs 图对应的顶点个数
* @param data 图的各个顶点的值
* @param weight 图的邻接矩阵
*/
public void createGraph(MGraph graph, int verxs, char data[], int[][] weight) {
int i, j;
for (i = 0; i < verxs; i++) {// 顶点
graph.data[i] = data[i];
for (j = 0; j < verxs; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
// 显示图的邻接矩阵
public void showGraph(MGraph graph) {
for (int[] link : graph.weight) {
System.out.println(Arrays.toString(link));
}
}
}# 6.5.2、普林姆算法
- 编写普林姆算法
//创建最小生成树->村庄的图
class MinTree {
//编写prim算法,得到最小生成树
/**
*
* @param graph 图
* @param v 表示从图的第几个顶点开始生成,'A'->0 'B'->1...
*/
public void prim(MGraph graph, int v) {
// visited[] 标记结点(顶点)是否被访问过
int visited[] = new int[graph.verxs];
// 把当前这个结点标记为已访问
visited[v] = 1;
// h1 和 h2 记录两个顶点的下标
int h1 = -1;
int h2 = -1;
int minWeight = 10000; // 将 minWeight 初始成一个大数,后面在遍历过程中,会被替换
for (int k = 1; k < graph.verxs; k++) {// 因为有 graph.verxs顶点,普利姆算法结束后,有 graph.verxs-1边
// 这个是确定每一次生成的子图 ,和哪个结点的距离最近
for (int i = 0; i < graph.verxs; i++) {// i结点表示被访问过的结点
for (int j = 0; j < graph.verxs; j++) {// j结点表示还没有访问过的结点
if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {
// 替换minWeight(寻找已经访问过的结点和未访问过的结点间的权值最小的边)
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}
}
// 找到一条边是最小
System.out.println("边<" + graph.data[h1] + "," + graph.data[h2] + "> 权值:" + minWeight);
// 将当前这个结点标记为已经访问
visited[h2] = 1;
// minWeight 重新设置为最大值 10000
minWeight = 10000;
}
}
}# 6.5.3、代码测试
- 代码
public static void main(String[] args) {
//测试看看图是否创建ok
char[] data = new char[]{'A','B','C','D','E','F','G'};
int verxs = data.length;
//邻接矩阵的关系使用二维数组表示,10000这个大数,表示两个点不联通
int [][]weight=new int[][]{
{10000,5,7,10000,10000,10000,2},
{5,10000,10000,9,10000,10000,3},
{7,10000,10000,10000,8,10000,10000},
{10000,9,10000,10000,10000,4,10000},
{10000,10000,8,10000,10000,5,4},
{10000,10000,10000,4,5,10000,6},
{2,3,10000,10000,4,6,10000}
};
//创建MGraph对象
MGraph graph = new MGraph(verxs);
//创建一个MinTree对象
MinTree minTree = new MinTree();
graph.createGraph(graph, verxs, data, weight);
//输出
graph.showGraph(graph);
//测试普利姆算法
minTree.prim(graph, 0);
}- 程序运行结果
[10000, 5, 7, 10000, 10000, 10000, 2]
[5, 10000, 10000, 9, 10000, 10000, 3]
[7, 10000, 10000, 10000, 8, 10000, 10000]
[10000, 9, 10000, 10000, 10000, 4, 10000]
[10000, 10000, 8, 10000, 10000, 5, 4]
[10000, 10000, 10000, 4, 5, 10000, 6]
[2, 3, 10000, 10000, 4, 6, 10000]
边<A,G> 权值:2
边<G,B> 权值:3
边<G,E> 权值:4
边<E,F> 权值:5
边<F,D> 权值:4
边<A,C> 权值:7# 6.6、普利姆算法全部代码
public class PrimAlgorithm {
public static void main(String[] args) {
//测试看看图是否创建ok
char[] data = new char[]{'A','B','C','D','E','F','G'};
int verxs = data.length;
//邻接矩阵的关系使用二维数组表示,10000这个大数,表示两个点不联通
int [][]weight=new int[][]{
{10000,5,7,10000,10000,10000,2},
{5,10000,10000,9,10000,10000,3},
{7,10000,10000,10000,8,10000,10000},
{10000,9,10000,10000,10000,4,10000},
{10000,10000,8,10000,10000,5,4},
{10000,10000,10000,4,5,10000,6},
{2,3,10000,10000,4,6,10000}
};
//创建MGraph对象
MGraph graph = new MGraph(verxs);
//创建一个MinTree对象
MinTree minTree = new MinTree();
graph.createGraph(graph, verxs, data, weight);
//输出
graph.showGraph(graph);
//测试普利姆算法
minTree.prim(graph, 0);//
}
}
//创建最小生成树->村庄的图
class MinTree {
//编写prim算法,得到最小生成树
/**
*
* @param graph 图
* @param v 表示从图的第几个顶点开始生成,'A'->0 'B'->1...
*/
public void prim(MGraph graph, int v) {
// visited[] 标记结点(顶点)是否被访问过
int visited[] = new int[graph.verxs];
// 把当前这个结点标记为已访问
visited[v] = 1;
// h1 和 h2 记录两个顶点的下标
int h1 = -1;
int h2 = -1;
int minWeight = 10000; // 将 minWeight 初始成一个大数,后面在遍历过程中,会被替换
for (int k = 1; k < graph.verxs; k++) {// 因为有 graph.verxs顶点,普利姆算法结束后,有 graph.verxs-1边
// 这个是确定每一次生成的子图 ,和哪个结点的距离最近
for (int i = 0; i < graph.verxs; i++) {// i结点表示被访问过的结点
for (int j = 0; j < graph.verxs; j++) {// j结点表示还没有访问过的结点
if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {
// 替换minWeight(寻找已经访问过的结点和未访问过的结点间的权值最小的边)
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}
}
// 找到一条边是最小
System.out.println("边<" + graph.data[h1] + "," + graph.data[h2] + "> 权值:" + minWeight);
// 将当前这个结点标记为已经访问
visited[h2] = 1;
// minWeight 重新设置为最大值 10000
minWeight = 10000;
}
}
}
class MGraph {
int verxs; // 表示图的节点个数
char[] data;// 存放结点数据
int[][] weight; // 存放边,就是我们的邻接矩阵
public MGraph(int verxs) {
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
//创建图的邻接矩阵
/**
*
* @param graph 图对象
* @param verxs 图对应的顶点个数
* @param data 图的各个顶点的值
* @param weight 图的邻接矩阵
*/
public void createGraph(MGraph graph, int verxs, char data[], int[][] weight) {
int i, j;
for (i = 0; i < verxs; i++) {// 顶点
graph.data[i] = data[i];
for (j = 0; j < verxs; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
// 显示图的邻接矩阵
public void showGraph(MGraph graph) {
for (int[] link : graph.weight) {
System.out.println(Arrays.toString(link));
}
}
}# 7、克鲁斯卡尔算法
# 7.1、应用场景 (公交站问题)
- 看一个应用场景和问题:
- 某城市新增 7 个站点 (A, B, C, D, E, F, G) ,现在需要修路把 7 个站点连通
- 各个站点的距离用边线表示 (权) ,比如 A – B 距离 12 公里
- 问:如何修路保证各个站点都能连通,并且总的修建公路总里程最短?
# 7.2、克鲁斯卡尔算法介绍
- 克鲁斯卡尔 (Kruskal) 算法,是用来求加权连通图的最小生成树的算法。
- 基本思想:按照权值从小到大的顺序选择 n-1 条边,并保证这 n-1 条边不构成回路
- 具体做法:首先构造一个只含 n 个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中,并使森林中不产生回路,直至森林变成一棵树为止
# 7.3、代码思路
# 7.3.1、最小生成树
- 在含有 n 个顶点的连通图中选择 n-1 条边,构成一棵极小连通子图,并使该连通子图中 n-1 条边上权值之和达到最小,则称其为连通网的最小生成树
- 例如,对于如上图 G4 所示的连通网可以有多棵权值总和不相同的生成树。
# 7.3.2、克鲁斯卡尔算法图解
- 以上图 G4 为例,来对克鲁斯卡尔进行演示 (假设,用数组 R 保存最小生成树结果)
- 第 1 步:将边 <E,F> 加入 R 中。 边 < E,F > 的权值最小,因此将它加入到最小生成树结果 R 中。
- 第 2 步:将边 <C,D> 加入 R 中。 上一步操作之后,边 < C,D > 的权值最小,因此将它加入到最小生成树结果 R 中。
- 第 3 步:将边 <D,E> 加入 R 中。 上一步操作之后,边 < D,E > 的权值最小,因此将它加入到最小生成树结果 R 中。
- 第 4 步:将边 <B,F> 加入 R 中。 上一步操作之后,边 < C,E > 的权值最小,但 < C,E > 会和已有的边构成回路;因此,跳过边 < C,E>。同理,跳过边 < C,F>。将边 < B,F > 加入到最小生成树结果 R 中。
- 第 5 步:将边 <E,G> 加入 R 中。 上一步操作之后,边 < E,G > 的权值最小,因此将它加入到最小生成树结果 R 中。
- 第 6 步:将边 <A,B> 加入 R 中。 上一步操作之后,边 < F,G > 的权值最小,但 < F,G > 会和已有的边构成回路;因此,跳过边 < F,G>。同理,跳过边 < B,C>。将边 < A,B > 加入到最小生成树结果 R 中。
- 此时,最小生成树构造完成!它包括的边依次是:<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。
- 总结:
- 将所有边按照权值排序,从小到大依次加入森林中
- 前提条件:森林中不产生回路,因为产生回路,这条路就相当于是多余的,就算它权值再小也没卵用
# 7.4、克鲁斯卡尔算法分析
- 根据前面介绍的克鲁斯卡尔算法的基本思想和做法,我们能够了解到,克鲁斯卡尔算法重点需要解决的以下两个问题:
- 问题一:对图的所有边按照权值大小进行排序?采用排序算法进行排序即可。
- 问题二:将边添加到最小生成树中时,怎么样判断是否形成了回路?处理方式是:
- 记录顶点在 "最小生成树" 中的终点,顶点的终点是 "在最小生成树中与它连通的最大顶点"
- 然后每次需要将一条边添加到最小生存树时,判断该边的两个顶点的终点是否重合,重合的话则会构成回路
- 想想为什么能这样判断是否形成了回路?下面举例说明
- 在将 <E,F> <C,D> <D,E > 加入到最小生成树 R 中之后,这几条边的顶点就都有了终点
- C 的终点是 F
- D 的终点是 F
- E 的终点是 F
- F 的终点是 F
- 关于终点的说明:
- 就是将所有顶点按照从小到大的顺序排列好之后;某个顶点的终点就是与它连通的最大顶点。
- 因此,接下来,虽然 <C,E> 是权值最小的边。但是 C 和 E 的终点都是 F,即它们的终点相同,因此,将 < C,E > 加入最小生成树的话,会形成回路。
- 这就是判断回路的方式。也就是说,我们加入的边的两个顶点不能都指向同一个终点,否则将构成回路
- 为啥添加边时,该边的两个顶点的终点重合,他们两就指向同一个构成回路?两个顶点的终点重合,就说明这两个顶点都能寻找到一条路径,跑到终点处,再为这两个顶点添加一条边,就是画蛇添足,只会增加总路径的长度
- 在将 <E,F> <C,D> <D,E > 加入到最小生成树 R 中之后,这几条边的顶点就都有了终点
# 7.5、代码实现
# 7.5.1、边的定义
- 定义 EdgeData 类,用于表示一条边
//创建一个类EData ,它的对象实例就表示一条边
class EdgeData {
char start; // 边的一个点
char end; // 边的另外一个点
int weight; // 边的权值
// 构造器
public EdgeData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
// 重写toString, 便于输出边信息
@Override
public String toString() {
return "EData [<" + start + ", " + end + ">= " + weight + "]";
}
}# 7.5.2、克鲁斯卡尔算法
- sortEdges () 方法:按照边的路径长度,对边进行排序
- getPosition () 方法:根据顶点的名称返回其索引值
- getEdges () 方法:根据邻接矩阵返回边的数组(EdgeData [])
- getEnd () 方法:返回索引为 i 的顶点的终点,具体做法如下:
- ends [i] 拿到索引为 i 的节点的邻接点
- 令 i = ends [i] ,再通过 ends [i] 拿到其邻接点
- 直至 ends [i] == 0 时,说明索引为 i 的节点(注意 i 一直在变化)就是终点
- kruskal () 方法:利用克鲁斯卡尔算法生成最小生成树:
- 首选按照边的路径长度,对边进行排序
- 遍历每条边的顶点,计算两个顶点的终点
- 如果顶点的终点不重合,则记录当前当前边两个顶点共同的终点
- 否则,该路径构成回路,啥也不做
- 再来看看精髓之处,如何记录顶点的终点?ends [endPointOfPoint1] = endPointOfPoint2;
- 就以上面的例子来说明,现在有 7 个顶点,ends 数组长度为 7 ,用于记录顶点的索引
- 第一次遍历时 <E, F>= 2 ,其路径最短 ,记录 E(索引为 4) 的终点为 F(索引为 5 ) ,即 ends [4] = 5
- 第二次遍历时 <C, D>= 3 ,其路径最短 ,记录 C(索引为 2) 的终点为 D(索引为 3 ) ,即 ends [2] = 3
- 第三次遍历时 <D, E>= 3 ,其路径最短 ,记录 D(索引为 3) 的终点为 E(索引为 4 ) ,即 ends [3] = 4
- 其实,这有点链表的意思,我们通过 C 能找到 E
- C --> D :顶点 C 的索引为 2 ,令 i = 2 ,i = ends [i] = 3 ,即通过顶点 C 找到了顶点 D(索引为 3 )
- D --> E :顶点 D 的索引为 3 ,令 i = 3 ,i = ends [i] = 4 ,即通过顶点 D 找到了顶点 E(索引为 4 )
- 数组中元素值为零是什么意思?表示该顶点没有邻接点,即孤零零的一个,每个孤立点的终点我们认为就是他自己
class KruskalCase{
private int edgeNum; //边的个数
private char[] vertexs; //顶点数组
private int[][] matrix; //邻接矩阵
//使用 INF 表示两个顶点不能连通
private static final int INF = Integer.MAX_VALUE;
// 构造器
public KruskalCase(char[] vertexs, int[][] matrix) {
// 初始化顶点数和边的个数
int vlen = vertexs.length;
// 初始化顶点, 复制拷贝的方式
this.vertexs = new char[vlen];
for (int i = 0; i < vertexs.length; i++) {
this.vertexs[i] = vertexs[i];
}
// 初始化边, 使用的是复制拷贝的方式
this.matrix = new int[vlen][vlen];
for (int i = 0; i < vlen; i++) {
for (int j = 0; j < vlen; j++) {
this.matrix[i][j] = matrix[i][j];
}
}
// 统计边的条数
for (int i = 0; i < vlen; i++) {
for (int j = i + 1; j < vlen; j++) {
if (this.matrix[i][j] != INF) {
edgeNum++;
}
}
}
}
//打印邻接矩阵
public void print() {
System.out.println("邻接矩阵为: \n");
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
System.out.printf("%12d", matrix[i][j]);
}
System.out.println();// 换行
}
}
/**
* 功能:对边进行排序处理, 冒泡排序
* @param edges 边的集合
*/
private void sortEdges(EdgeData[] edges) {
for (int i = 0; i < edges.length - 1; i++) {
for (int j = 0; j < edges.length - 1 - i; j++) {
if (edges[j].weight > edges[j + 1].weight) {// 交换
EdgeData tmp = edges[j];
edges[j] = edges[j + 1];
edges[j + 1] = tmp;
}
}
}
}
/**
*
* @param ch 顶点的值,比如'A','B'
* @return 返回ch顶点对应的下标,如果找不到,返回-1
*/
private int getPosition(char ch) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == ch) {// 找到
return i;
}
}
// 找不到,返回-1
return -1;
}
/**
* 功能: 获取图中边,放到EData[] 数组中,后面我们需要遍历该数组
* 是通过matrix 邻接矩阵来获取
* EData[] 形式 [['A','B', 12], ['B','F',7], .....]
* @return
*/
private EdgeData[] getEdges() {
int index = 0;
EdgeData[] edges = new EdgeData[edgeNum];
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) {
if (matrix[i][j] != INF) {
edges[index++] = new EdgeData(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges;
}
/**
* 功能: 获取下标为i的顶点的终点, 用于后面判断两个顶点的终点是否相同
* @param ends : 数组就是记录了各个顶点对应的终点是哪个,ends 数组是在遍历过程中,逐步形成
* @param i : 表示传入的顶点对应的下标
* @return 返回的就是 下标为i的这个顶点对应的终点的下标, 一会回头还有来理解
*/
private int getEnd(int[] ends, int i) { // i = 4 [0,0,0,0,5,0,0,0,0,0,0,0]
while (ends[i] != 0) {
i = ends[i];
}
return i;
}
public void kruskal() {
int index = 0; // 表示最后结果数组的索引
int[] ends = new int[vertexs.length]; // 用于保存"已有最小生成树" 中的每个顶点在最小生成树中的终点
// 创建结果数组, 保存最后的最小生成树
EdgeData[] rets = new EdgeData[edgeNum];
// 获取图中 所有的边的集合 , 一共有12边
EdgeData[] edges = getEdges();
System.out.println("排序前,图的边的集合=" + Arrays.toString(edges) + " 共" + edges.length); // 12
// 按照边的权值大小进行排序(从小到大)
sortEdges(edges);
System.out.println("排序后,图的边的集合=" + Arrays.toString(edges) + " 共" + edges.length); // 12
// 遍历edges 数组,将边添加到最小生成树中时,判断是准备加入的边否形成了回路,如果没有,就加入 rets, 否则不能加入
for (int i = 0; i < edgeNum; i++) {
// 获取到第i条边的第一个顶点(起点)
int p1 = getPosition(edges[i].start); // p1 = 4
// 获取到第i条边的第2个顶点
int p2 = getPosition(edges[i].end); // p2 = 5
// 获取p1这个顶点在已有最小生成树中的终点
int m = getEnd(ends, p1); // m = 4
// 获取p2这个顶点在已有最小生成树中的终点
int n = getEnd(ends, p2); // n = 5
// 是否构成回路
if (m != n) { // 没有构成回路
ends[m] = n; // 设置m 在"已有最小生成树"中的终点 <E,F> [0,0,0,0,5,0,0,0,0,0,0,0]
rets[index++] = edges[i]; // 有一条边加入到rets数组
}
}
// <E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。
// 统计并打印 "最小生成树", 输出 rets
System.out.println("最小生成树为");
for (int i = 0; i < index; i++) {
System.out.println(rets[i]);
}
}
}# 7.5.3、测试代码
- 代码
//使用 INF 表示两个顶点不能连通
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//克鲁斯卡尔算法的邻接矩阵
int matrix[][] = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ { 0, 12, INF, INF, INF, 16, 14},
/*B*/ { 12, 0, 10, INF, INF, 7, INF},
/*C*/ { INF, 10, 0, 3, 5, 6, INF},
/*D*/ { INF, INF, 3, 0, 4, INF, INF},
/*E*/ { INF, INF, 5, 4, 0, 2, 8},
/*F*/ { 16, 7, 6, INF, 2, 0, 9},
/*G*/ { 14, INF, INF, INF, 8, 9, 0}};
//大家可以在去测试其它的邻接矩阵,结果都可以得到最小生成树.
//创建KruskalCase 对象实例
KruskalCase kruskalCase = new KruskalCase(vertexs, matrix);
//输出构建的
kruskalCase.print();
kruskalCase.kruskal();
} - 程序运行结果
邻接矩阵为:
0 12 2147483647 2147483647 2147483647 16 14
12 0 10 2147483647 2147483647 7 2147483647
2147483647 10 0 3 5 6 2147483647
2147483647 2147483647 3 0 4 2147483647 2147483647
2147483647 2147483647 5 4 0 2 8
16 7 6 2147483647 2 0 9
14 2147483647 2147483647 2147483647 8 9 0
排序前,图的边的集合=[EData [<A, B>= 12], EData [<A, F>= 16], EData [<A, G>= 14], EData [<B, C>= 10], EData [<B, F>= 7], EData [<C, D>= 3], EData [<C, E>= 5], EData [<C, F>= 6], EData [<D, E>= 4], EData [<E, F>= 2], EData [<E, G>= 8], EData [<F, G>= 9]] 共12
排序后,图的边的集合=[EData [<E, F>= 2], EData [<C, D>= 3], EData [<D, E>= 4], EData [<C, E>= 5], EData [<C, F>= 6], EData [<B, F>= 7], EData [<E, G>= 8], EData [<F, G>= 9], EData [<B, C>= 10], EData [<A, B>= 12], EData [<A, G>= 14], EData [<A, F>= 16]] 共12
最小生成树为
EData [<E, F>= 2]
EData [<C, D>= 3]
EData [<D, E>= 4]
EData [<B, F>= 7]
EData [<E, G>= 8]
EData [<A, B>= 12]# 7.6、克鲁斯卡尔算法全部代码
public class KruskalCaseDemo {
//使用 INF 表示两个顶点不能连通
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//克鲁斯卡尔算法的邻接矩阵
int matrix[][] = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ { 0, 12, INF, INF, INF, 16, 14},
/*B*/ { 12, 0, 10, INF, INF, 7, INF},
/*C*/ { INF, 10, 0, 3, 5, 6, INF},
/*D*/ { INF, INF, 3, 0, 4, INF, INF},
/*E*/ { INF, INF, 5, 4, 0, 2, 8},
/*F*/ { 16, 7, 6, INF, 2, 0, 9},
/*G*/ { 14, INF, INF, INF, 8, 9, 0}};
//大家可以在去测试其它的邻接矩阵,结果都可以得到最小生成树.
//创建KruskalCase 对象实例
KruskalCase kruskalCase = new KruskalCase(vertexs, matrix);
//输出构建的
kruskalCase.print();
kruskalCase.kruskal();
}
}
class KruskalCase{
private int edgeNum; //边的个数
private char[] vertexs; //顶点数组
private int[][] matrix; //邻接矩阵
//使用 INF 表示两个顶点不能连通
private static final int INF = Integer.MAX_VALUE;
// 构造器
public KruskalCase(char[] vertexs, int[][] matrix) {
// 初始化顶点数和边的个数
int vlen = vertexs.length;
// 初始化顶点, 复制拷贝的方式
this.vertexs = new char[vlen];
for (int i = 0; i < vertexs.length; i++) {
this.vertexs[i] = vertexs[i];
}
// 初始化边, 使用的是复制拷贝的方式
this.matrix = new int[vlen][vlen];
for (int i = 0; i < vlen; i++) {
for (int j = 0; j < vlen; j++) {
this.matrix[i][j] = matrix[i][j];
}
}
// 统计边的条数
for (int i = 0; i < vlen; i++) {
for (int j = i + 1; j < vlen; j++) {
if (this.matrix[i][j] != INF) {
edgeNum++;
}
}
}
}
//打印邻接矩阵
public void print() {
System.out.println("邻接矩阵为: \n");
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
System.out.printf("%12d", matrix[i][j]);
}
System.out.println();// 换行
}
}
/**
* 功能:对边进行排序处理, 冒泡排序
* @param edges 边的集合
*/
private void sortEdges(EdgeData[] edges) {
for (int i = 0; i < edges.length - 1; i++) {
for (int j = 0; j < edges.length - 1 - i; j++) {
if (edges[j].weight > edges[j + 1].weight) {// 交换
EdgeData tmp = edges[j];
edges[j] = edges[j + 1];
edges[j + 1] = tmp;
}
}
}
}
/**
*
* @param ch 顶点的值,比如'A','B'
* @return 返回ch顶点对应的下标,如果找不到,返回-1
*/
private int getPosition(char ch) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == ch) {// 找到
return i;
}
}
// 找不到,返回-1
return -1;
}
/**
* 功能: 获取图中边,放到EData[] 数组中,后面我们需要遍历该数组
* 是通过matrix 邻接矩阵来获取
* EData[] 形式 [['A','B', 12], ['B','F',7], .....]
* @return
*/
private EdgeData[] getEdges() {
int index = 0;
EdgeData[] edges = new EdgeData[edgeNum];
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) {
if (matrix[i][j] != INF) {
edges[index++] = new EdgeData(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges;
}
/**
* 功能: 获取下标为i的顶点的终点, 用于后面判断两个顶点的终点是否相同
* @param ends : 数组就是记录了各个顶点对应的终点是哪个,ends 数组是在遍历过程中,逐步形成
* @param i : 表示传入的顶点对应的下标
* @return 返回的就是 下标为i的这个顶点对应的终点的下标, 一会回头还有来理解
*/
private int getEnd(int[] ends, int i) { // i = 4 [0,0,0,0,5,0,0,0,0,0,0,0]
while (ends[i] != 0) {
i = ends[i];
}
return i;
}
public void kruskal() {
int index = 0; // 表示最后结果数组的索引
int[] ends = new int[vertexs.length]; // 用于保存"已有最小生成树" 中的每个顶点在最小生成树中的终点
// 创建结果数组, 保存最后的最小生成树
EdgeData[] rets = new EdgeData[edgeNum];
// 获取图中 所有的边的集合 , 一共有12边
EdgeData[] edges = getEdges();
System.out.println("排序前,图的边的集合=" + Arrays.toString(edges) + " 共" + edges.length); // 12
// 按照边的权值大小进行排序(从小到大)
sortEdges(edges);
System.out.println("排序后,图的边的集合=" + Arrays.toString(edges) + " 共" + edges.length); // 12
// 遍历edges 数组,将边添加到最小生成树中时,判断是准备加入的边否形成了回路,如果没有,就加入 rets, 否则不能加入
for (int i = 0; i < edgeNum; i++) {
// 获取到第i条边的第一个顶点(起点)
int point1 = getPosition(edges[i].start); // point1 = 4
// 获取到第i条边的第2个顶点
int point2 = getPosition(edges[i].end); // point2 = 5
// 获取p1这个顶点在已有最小生成树中的终点
int endPointOfPoint1 = getEnd(ends, point1); // endPointOfPoint1 = 4
// 获取p2这个顶点在已有最小生成树中的终点
int endPointOfPoint2 = getEnd(ends, point2); // endPointOfPoint2 = 5
// 是否构成回路
if (endPointOfPoint1 != endPointOfPoint2) { // 没有构成回路
ends[endPointOfPoint1] = endPointOfPoint2; // 设置m 在"已有最小生成树"中的终点 <E,F> [0,0,0,0,5,0,0,0,0,0,0,0]
rets[index++] = edges[i]; // 有一条边加入到rets数组
}
}
// <E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。
// 统计并打印 "最小生成树", 输出 rets
System.out.println("最小生成树为");
for (int i = 0; i < index; i++) {
System.out.println(rets[i]);
}
}
}
//创建一个类EData ,它的对象实例就表示一条边
class EdgeData {
char start; // 边的一个点
char end; // 边的另外一个点
int weight; // 边的权值
// 构造器
public EdgeData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
// 重写toString, 便于输出边信息
@Override
public String toString() {
return "EData [<" + start + ", " + end + ">= " + weight + "]";
}
}# 8、迪杰斯特拉算法
# 8.1、应用场景 (最短路径问题)
- 看一个应用场景和问题:
- 战争时期,胜利乡有 7 个村庄 (A, B, C, D, E, F, G) ,现在有六个邮差,从 G 点出发,需要分别把邮件分别送到 A, B, C , D, E, F 六个村庄
- 各个村庄的距离用边线表示 (权) ,比如 A – B 距离 5 公里
- 问:如何计算出 G 村庄到 其它各个村庄的最短距离?
- 如果从其它点出发到各个点的最短距离又是多少?
# 8.2、迪杰斯特拉算法介绍
- 迪杰斯特拉 (Dijkstra) 算法是典型最短路径算法,用于计算一个结点到其他结点的最短路径。 它的主要特点是以起始点为中心向外层层扩展 (广度优先搜索思想),直到扩展到终点为止。
# 8.3、迪杰斯特拉算法过程
- 两个重要的集合(辅助实现迪杰斯特拉算法):
- 设置出发顶点为 v,顶点集合 V {v1,v2,vi…},
- v 到 V 中各顶点的距离构成距离集合 Dis,Dis {d1,d2,di…},Dis 集合记录着 v 到图中各顶点的距离 (到自身可以看作 0,v 到 vi 距离对应为 di)
- 算法流程
- 从 Dis 中选择值最小的 di 并移出 Dis 集合,同时移出 V 集合中对应的顶点 vi,此时的 v 到 vi 即为最短路径
- 更新 Dis 集合,更新规则为:比较 v 到 V 集合中顶点的距离值,与 v 通过 vi 到 V 集合中顶点的距离值,保留值较小的一个 (同时也应该更新顶点的前驱节点为 vi,表明是通过 vi 到达的)
- 重复执行两步骤,直到最短路径顶点为目标顶点即可结束
# 8.4、迪杰斯特拉算法图解
- 在地杰斯特拉算法中,有三个非常重要的数组
class Visited_vertex{//已访问顶点集合
public int[] already_arr; //记录各个顶点是否访问过 1表示访问过,0未访问,会动态更新
public int[] dis;//记录出发顶点到其他所有顶点的距离,比如G为出发顶点,就会记录G到其它顶点的距离,会动态更新,求的最短距离就会存放到dis
public int[] pre_visited;//每个下标对应的值为前一个顶点下标, 会动态更新
}-
以下面这个图为例,该图一共有 {A, B, C, D, E ,F, G} 七个顶点,比如说需要从 G --> C ,G --> D 的最短路径
- 初始情况:
- already_arr = {0, 0, 0, 0, 0, 0, 0} ,表示当前还未访问过任何顶点
- dis = {N, N, N, N, N, N, N} ,N 表示出发顶点与目标顶点的距离无穷大,因为后面程序中需要选取最小值,所以初始时,将 dis 全部元素设置成无穷大,很合理
- pre_visited = {0, 0, 0, 0, 0, 0, 0} ,初始值默认为 0 ,我感觉有歧义啊。。。我感觉初始值应该为 -1
- 以 G 为出发顶点
- already_arr = {0, 0, 0, 0, 0, 0, 1} ,表示顶点 G 已被访问过
- dis = {N, N, N, N, N, N, 0} ,顶点 G 就是出发顶点,距离为 0
- pre_visited = {0, 0, 0, 0, 0, 0, 0} ,出发顶点没有前一个顶点
- 以 G 点为初始顶点,尝试访问其邻接点 {A, B, E, F} ,并找出下一步路径最短的走法
- already_arr = {0, 0, 0, 0, 0, 0, 1} ,现在是在尝试访问顶点 G 的邻接点,并不是真正在访问,所以不能将顶点 { A, B, E, F } 标记为已访问
- dis = {2, 3, N, N, 4, 6, 0} ,出发顶点 G --> A 的距离最短,并且顶点 A 并没有被访问过,可以选取顶点 A 作为下一次的初始顶点
- pre_visited = {6, 6, 0, 0, 6, 6, 0} ,标记顶点 { A, B, E, F } 的前一个顶点为 G
- 此时在所有路径中,G --> A 路径最短,并且顶点 A 没有被访问过,所以 A 点为初始顶点,尝试访问其邻接点 {B, C, G} ,并找出下一步路径最短的走法
- already_arr = {1, 0, 0, 0, 0, 0, 1} ,访问过顶点 A 之后,将其标记为已访问
- 分析 dis 数组的赋值流程:
- 由于 G 点已经被访问过了,所以不再访问 G 点
- 尝试走 G --> A --> B 这条路,距离为 2 + 5 = 7 ,但是之前有条路 G --> B 距离为 3 ,所以不做改变
- 尝试走 G --> A --> C 这条路,距离为 2 + 7 = 9 ,比之前的距离小,选择当前走法,标记出发点 G 到顶点 C 距离为 9 ,标记顶点 C 的前一个节点为顶点 A
- 综上分析: dis =
- pre_visited = {6, 6, 0, 0, 6, 6, 0} ,标记顶点 C 的前一个顶点为 A
- 此时在所有路径中,G --> B 路径最短,并且顶点 B 没有被访问过,所以 B 点为初始顶点,尝试访问其邻接点 {A, D, G} ,并找出下一步路径最短的走法
- already_arr = {1, 1, 0, 0, 0, 0, 1} ,访问过顶点 B 之后,将其标记为已访问
- 分析 dis 数组的赋值流程:
- 由于 A 点已经被访问过了,所以不再访问 A 点
- 为什么不再访问顶点 A ?那万一 G --> B --> A 的距离小于 G --> A 的距离呢?
- 如果 length (G --> B --> A) < length (G --> A),那肯定就说明 length (G --> B) < length (G --> A)
- 那肯定要先走顶点 B ,先走了顶点 A 即说明出发点到顶点 A 的距离是所有路径中最短的那条,所以无需再访问顶点 A
- 尝试走 G --> B --> D 这条路,距离为 3 + 9 = 12 ,目前来说,出发点距离顶点 D 的最短路径为 12,标记顶点 D 的前一个节点为顶点 B
- 由于 G 点已经被访问过了,所以不再访问 G 点
- 综上分析: dis =
- 由于 A 点已经被访问过了,所以不再访问 A 点
- pre_visited = {6, 6, 0, 1, 6, 6, 0} ,标记顶点 D 的前一个节点为顶点 B
- 此时在所有路径中,G --> E 路径最短,并且顶点 E 没有被访问过,所以 E 点为初始顶点,尝试访问其邻接点 {C, F, G} ,并找出下一步路径最短的走法
- already_arr = {1, 1, 0, 0, 1, 0, 1} ,访问过顶点 E 之后,将其标记为已访问
- 分析 dis 数组的赋值流程:
- 尝试走 G --> E --> C 这条路,距离为 4 + 8 = 12 ,但是之前有条路 G --> A --> C 距离为 8 ,所以不做改变
- 尝试走 G --> E --> F 这条路,距离为 4 + 5 = 9 ,但是之前有条路 G --> F 距离为 6 ,所以不做改变
- 由于 G 点已经被访问过了,所以不再访问 G 点
- 综上分析: dis =
- pre_visited = {6, 6, 0, 1, 6, 6, 0} ,本次未找到路径举例比上次短的,不做修改
- 此时在所有路径中,G --> F 路径最短,并且顶点 F 没有被访问过,所以 F 点为初始顶点,尝试访问其邻接点 {E, D, G} ,并找出下一步路径最短的走法
- already_arr = {1, 1, 0, 0, 1, 1, 1} ,访问过顶点 E 之后,将其标记为已访问
- 分析 dis 数组的赋值流程:
- 尝试走 G --> F --> D 这条路,距离为 6 + 4 = 10 ,之前有条路 G --> B --> D 距离为 12 ,这次距离比上次短,选择当前走法,标记出发点 G 到顶点 D 距离为 10 ,标记顶点 D 的前一个节点为顶点 F
- 由于 E 点已经被访问过了,所以不再访问 E 点
- 由于 G 点已经被访问过了,所以不再访问 G 点
- 综上分析: dis =
- pre_visited = {6, 6, 0, 5, 6, 6, 0} ,标记顶点 D 的前一个节点为顶点 F
- 此时在所有路径中,G --> A --> C 路径最短,并且顶点 C 没有被访问过,所以 C 点为初始顶点,尝试访问其邻接点 {A, E} ,发现顶点 { A, E } 均被访问过,说明走到的图的最深处,将顶点 C 标记已访问即可,其他两个数组不作处理
- 此时在所有路径中,G --> F --> D 路径最短,并且顶点 D 没有被访问过,所以 D 点为初始顶点,尝试访问其邻接点 {B, F} ,发现顶点 { B, F } 均被访问过,说明走到的图的最深处,将顶点 F 标记已访问即可,其他两个数组不作处理
- 至此,图的广度优先遍历已经完成
- 初始情况:
-
假如说有 n 个顶点,来想想循环的结束条件是啥?想想前面的最小生成树,n 个节点最少 n - 1 条边才能将所有顶点连通,所以图的广度优先遍历,最多遍历 n - 1 次,就能将出发顶点和最远的顶点连通
- 我把图竖着画,是不是就要好理解一些,广度优先可以这样理解:以出发顶点为根节点,将图分成一层一层的结构(就像树那样),禁止产生回溯(一条路径不能走两遍),然后在每层中选取距离最短的路径,这样得到的路径就是最短路径
# 8.5、迪杰斯特拉算法实现
# 8.5.1、图的定义
- VisitedVertex 类用于存储上面所说的三个重要数组:already_arr、pre_visited、dis
- VisitedVertex 类中还提供了一些方法:
- isVisited () 方法:判断该顶点是否被访问过
- updateDis () 方法:更新出发顶点距离当前顶点的距离
- updatePre () 方法:更新当前顶点的前一个节点
- getDis () 方法:获取当前顶点与出发顶点之间的距离
- findNextStartPoint () 方法:寻找下一个初始顶点(当前还未被访问过、并且与出发顶点距离最短的顶点)
- showArrays () 方法:打印三个重要数组
// 已访问顶点集合
class VisitedVertex {
// 记录各个顶点是否访问过 1表示访问过,0未访问,会动态更新
public int[] already_arr;
// 每个下标对应的值为前一个顶点下标, 会动态更新
public int[] pre_visited;
// 记录出发顶点到其他所有顶点的距离,比如G为出发顶点,就会记录G到其它顶点的距离,会动态更新,求的最短距离就会存放到dis
public int[] dis;
//构造器
/**
*
* @param length :表示顶点的个数
* @param index: 出发顶点对应的下标, 比如G顶点,下标就是6
*/
public VisitedVertex(int length, int index) {
this.already_arr = new int[length];
this.pre_visited = new int[length];
this.dis = new int[length];
// 初始化 dis数组
Arrays.fill(dis, 65535);
this.dis[index] = 0;// 设置出发顶点的访问距离为0
this.already_arr[index] = 1; // 设置出发顶点被访问过
}
/**
* 功能: 判断index顶点是否被访问过
* @param index
* @return 如果访问过,就返回true, 否则访问false
*/
public boolean isVisited(int index) {
return already_arr[index] == 1;
}
/**
* 功能: 更新出发顶点到index顶点的距离
* @param index
* @param len
*/
public void updateDis(int index, int len) {
dis[index] = len;
}
/**
* 功能: 更新pre这个顶点的前驱顶点为index顶点
* @param pre
* @param index
*/
public void updatePre(int pre, int index) {
pre_visited[pre] = index;
}
/**
* 功能:返回出发顶点到index顶点的距离
* @param index
*/
public int getDis(int index) {
return dis[index];
}
/**
* 继续选择并返回新的访问顶点, 比如这里的G 完后,就是 A点作为新的访问顶点(注意不是出发顶点)
* @return
*/
public int findNextStartPoint() {
int min = 65535, index = 0;
for (int i = 0; i < already_arr.length; i++) {
if (already_arr[i] == 0 && dis[i] < min) {
min = dis[i];
index = i;
}
}
// 更新 index 顶点被访问过
already_arr[index] = 1;
return index;
}
//显示最后的结果
//即将三个数组的情况输出
public void showArrays() {
System.out.println("核心数组的值如下:");
// 输出already_arr
for (int i : already_arr) {
System.out.print(i + " ");
}
System.out.println();
// 输出dis
for (int i : dis) {
System.out.print(i + " ");
}
System.out.println();
// 输出pre_visited
for (int i : pre_visited) {
System.out.print(i + " ");
}
System.out.println();
// 为了好看最后的最短距离,我们处理
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
int count = 0;
for (int i : dis) {
if (i != 65535) {
System.out.print(vertex[count] + "(" + i + ") ");
} else {
System.out.print("N ");
}
count++;
}
System.out.println();
System.out.println();
}
}# 8.5.2、迪杰斯特拉算法
- 迪杰斯特拉算法的流程:
- 计算初始顶点的邻接点与出发顶点的最短距离,记录在 dis 数组中,并标记当前初始顶点已经被访问
- 寻找下一个与出发顶点距离最近,并且没有访问过的顶点,作为下一次的初始定点
- 如此返回
- 上述操作执行 vertex.length - 1 次,就能保证求得最短路径
class Graph {
private char[] vertex; // 顶点数组
private int[][] matrix; // 邻接矩阵
private VisitedVertex vv; // 已经访问的顶点的集合
// 构造器
public Graph(char[] vertex, int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}
// 显示结果
public void showDijkstra() {
vv.showArrays();
}
// 显示图
public void showGraph() {
for (int[] link : matrix) {
for (int i : link) {
System.out.printf("%8d", i);
}
System.out.println();
}
}
//迪杰斯特拉算法实现
/**
*
* @param index 表示出发顶点对应的下标
*/
public void dsj(int index) {
vv = new VisitedVertex(vertex.length, index);
update(index);// 更新index顶点到周围顶点的距离和前驱顶点
vv.showArrays();
for (int j = 1; j < vertex.length; j++) {
index = vv.findNextStartPoint();// 选择并返回新的访问顶点
update(index); // 更新index顶点到周围顶点的距离和前驱顶点
vv.showArrays();
}
}
// 更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点,
private void update(int index) {
int len = 0;
// 根据遍历我们的邻接矩阵的 matrix[index]行
for (int j = 0; j < matrix[index].length; j++) {
// len 含义是 : 出发顶点到index顶点的距离 + 从index顶点到j顶点的距离的和
len = vv.getDis(index) + matrix[index][j];
// 如果j顶点没有被访问过,并且 len 小于出发顶点到j顶点的距离,就需要更新
if (!vv.isVisited(j) && len < vv.getDis(j)) {
vv.updatePre(j, index); // 更新j顶点的前驱为index顶点
vv.updateDis(j, len); // 更新出发顶点到j顶点的距离
}
}
}
}# 8.5.3、代码测试
- 代码
public static void main(String[] args) {
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
// 邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;// 表示不可以连接
matrix[0] = new int[] { N, 5, 7, N, N, N, 2 };
matrix[1] = new int[] { 5, N, N, 9, N, N, 3 };
matrix[2] = new int[] { 7, N, N, N, 8, N, N };
matrix[3] = new int[] { N, 9, N, N, N, 4, N };
matrix[4] = new int[] { N, N, 8, N, N, 5, 4 };
matrix[5] = new int[] { N, N, N, 4, 5, N, 6 };
matrix[6] = new int[] { 2, 3, N, N, 4, 6, N };
// 创建 Graph对象
Graph graph = new Graph(vertex, matrix);
// 测试, 看看图的邻接矩阵是否ok
graph.showGraph();
// 测试迪杰斯特拉算法
graph.dsj(6);// G
}- 程序运行结果
65535 5 7 65535 65535 65535 2
5 65535 65535 9 65535 65535 3
7 65535 65535 65535 8 65535 65535
65535 9 65535 65535 65535 4 65535
65535 65535 8 65535 65535 5 4
65535 65535 65535 4 5 65535 6
2 3 65535 65535 4 6 65535
核心数组的值如下:
0 0 0 0 0 0 1
2 3 65535 65535 4 6 0
6 6 0 0 6 6 0
A(2) B(3) N N E(4) F(6) G(0)
核心数组的值如下:
1 0 0 0 0 0 1
2 3 9 65535 4 6 0
6 6 0 0 6 6 0
A(2) B(3) C(9) N E(4) F(6) G(0)
核心数组的值如下:
1 1 0 0 0 0 1
2 3 9 12 4 6 0
6 6 0 1 6 6 0
A(2) B(3) C(9) D(12) E(4) F(6) G(0)
核心数组的值如下:
1 1 0 0 1 0 1
2 3 9 12 4 6 0
6 6 0 1 6 6 0
A(2) B(3) C(9) D(12) E(4) F(6) G(0)
核心数组的值如下:
1 1 0 0 1 1 1
2 3 9 10 4 6 0
6 6 0 5 6 6 0
A(2) B(3) C(9) D(10) E(4) F(6) G(0)
核心数组的值如下:
1 1 1 0 1 1 1
2 3 9 10 4 6 0
6 6 0 5 6 6 0
A(2) B(3) C(9) D(10) E(4) F(6) G(0)
核心数组的值如下:
1 1 1 1 1 1 1
2 3 9 10 4 6 0
6 6 0 5 6 6 0
A(2) B(3) C(9) D(10) E(4) F(6) G(0)# 8.6、迪杰斯特拉算法全部代码
public class DijkstraAlgorithm {
public static void main(String[] args) {
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
// 邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;// 表示不可以连接
matrix[0] = new int[] { N, 5, 7, N, N, N, 2 };
matrix[1] = new int[] { 5, N, N, 9, N, N, 3 };
matrix[2] = new int[] { 7, N, N, N, 8, N, N };
matrix[3] = new int[] { N, 9, N, N, N, 4, N };
matrix[4] = new int[] { N, N, 8, N, N, 5, 4 };
matrix[5] = new int[] { N, N, N, 4, 5, N, 6 };
matrix[6] = new int[] { 2, 3, N, N, 4, 6, N };
// 创建 Graph对象
Graph graph = new Graph(vertex, matrix);
// 测试, 看看图的邻接矩阵是否ok
graph.showGraph();
// 测试迪杰斯特拉算法
graph.dsj(6);// G
}
}
class Graph {
private char[] vertex; // 顶点数组
private int[][] matrix; // 邻接矩阵
private VisitedVertex vv; // 已经访问的顶点的集合
// 构造器
public Graph(char[] vertex, int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}
// 显示结果
public void showDijkstra() {
vv.showArrays();
}
// 显示图
public void showGraph() {
for (int[] link : matrix) {
for (int i : link) {
System.out.printf("%8d", i);
}
System.out.println();
}
}
//迪杰斯特拉算法实现
/**
*
* @param index 表示出发顶点对应的下标
*/
public void dsj(int index) {
vv = new VisitedVertex(vertex.length, index);
update(index);// 更新index顶点到周围顶点的距离和前驱顶点
vv.showArrays();
for (int j = 1; j < vertex.length; j++) {
index = vv.findNextStartPoint();// 选择并返回新的访问顶点
update(index); // 更新index顶点到周围顶点的距离和前驱顶点
vv.showArrays();
}
}
// 更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点,
private void update(int index) {
int len = 0;
// 根据遍历我们的邻接矩阵的 matrix[index]行
for (int j = 0; j < matrix[index].length; j++) {
// len 含义是 : 出发顶点到index顶点的距离 + 从index顶点到j顶点的距离的和
len = vv.getDis(index) + matrix[index][j];
// 如果j顶点没有被访问过,并且 len 小于出发顶点到j顶点的距离,就需要更新
if (!vv.isVisited(j) && len < vv.getDis(j)) {
vv.updatePre(j, index); // 更新j顶点的前驱为index顶点
vv.updateDis(j, len); // 更新出发顶点到j顶点的距离
}
}
}
}
// 已访问顶点集合
class VisitedVertex {
// 记录各个顶点是否访问过 1表示访问过,0未访问,会动态更新
public int[] already_arr;
// 每个下标对应的值为前一个顶点下标, 会动态更新
public int[] pre_visited;
// 记录出发顶点到其他所有顶点的距离,比如G为出发顶点,就会记录G到其它顶点的距离,会动态更新,求的最短距离就会存放到dis
public int[] dis;
//构造器
/**
*
* @param length :表示顶点的个数
* @param index: 出发顶点对应的下标, 比如G顶点,下标就是6
*/
public VisitedVertex(int length, int index) {
this.already_arr = new int[length];
this.pre_visited = new int[length];
this.dis = new int[length];
// 初始化 dis数组
Arrays.fill(dis, 65535);
this.dis[index] = 0;// 设置出发顶点的访问距离为0
this.already_arr[index] = 1; // 设置出发顶点被访问过
}
/**
* 功能: 判断index顶点是否被访问过
* @param index
* @return 如果访问过,就返回true, 否则访问false
*/
public boolean isVisited(int index) {
return already_arr[index] == 1;
}
/**
* 功能: 更新出发顶点到index顶点的距离
* @param index
* @param len
*/
public void updateDis(int index, int len) {
dis[index] = len;
}
/**
* 功能: 更新pre这个顶点的前驱顶点为index顶点
* @param pre
* @param index
*/
public void updatePre(int pre, int index) {
pre_visited[pre] = index;
}
/**
* 功能:返回出发顶点到index顶点的距离
* @param index
*/
public int getDis(int index) {
return dis[index];
}
/**
* 继续选择并返回新的访问顶点, 比如这里的G 完后,就是 A点作为新的访问顶点(注意不是出发顶点)
* @return
*/
public int findNextStartPoint() {
int min = 65535, index = 0;
for (int i = 0; i < already_arr.length; i++) {
if (already_arr[i] == 0 && dis[i] < min) {
min = dis[i];
index = i;
}
}
// 更新 index 顶点被访问过
already_arr[index] = 1;
return index;
}
//显示最后的结果
//即将三个数组的情况输出
public void showArrays() {
System.out.println("核心数组的值如下:");
// 输出already_arr
for (int i : already_arr) {
System.out.print(i + " ");
}
System.out.println();
// 输出dis
for (int i : dis) {
System.out.print(i + " ");
}
System.out.println();
// 输出pre_visited
for (int i : pre_visited) {
System.out.print(i + " ");
}
System.out.println();
// 为了好看最后的最短距离,我们处理
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
int count = 0;
for (int i : dis) {
if (i != 65535) {
System.out.print(vertex[count] + "(" + i + ") ");
} else {
System.out.print("N ");
}
count++;
}
System.out.println();
System.out.println();
}
}# 9、弗洛伊德算法
# 9.1、应用场景 (最短路径问题)
- 胜利乡有 7 个村庄 (A, B, C, D, E, F, G)
- 各个村庄的距离用边线表示 (权) ,比如 A – B 距离 5 公里
- 问:如何计算出各村庄到其它各村庄的最短距离?
# 9.2、弗洛伊德算法介绍
- 和 Dijkstra 算法一样,弗洛伊德 (Floyd) 算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978 年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特・弗洛伊德命名
- 弗洛伊德算法 (Floyd) 计算图中各个顶点之间的最短路径
- 迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径。
- 弗洛伊德算法 VS 迪杰斯特拉算法:
- 迪杰斯特拉算法通过选定的被访问顶点,求出从出发访问顶点到其他顶点的最短路径;
- 弗洛伊德算法中每一个顶点都是出发访问点,所以需要将每一个顶点看做被访问顶点,求出从每一个顶点到其他顶点的最短路径。
# 9.3、弗洛伊德算法分析
- 设置顶点 vi 到顶点 vk 的最短路径已知为 Lik,顶点 vk 到 vj 的最短路径已知为 Lkj,顶点 vi 到 vj 的路径为 Lij,则 vi 到 vj 的最短路径为:min ((Lik+Lkj),Lij),vk 的取值为图中所有顶点,则可获得 vi 到 vj 的最短路径
- 至于 vi 到 vk 的最短路径 Lik 或者 vk 到 vj 的最短路径 Lkj,也是以同样的方式获得
# 9.4、弗洛伊德算法图解
- 弗洛伊德算法中有两个核心的二维数组:
- dis :二维数组,记录顶点 i 到顶点 j 的距离:
dis[i][j]或dis[j][i] - pre :二维数组,记录顶点 i 和顶点 j 的前驱顶点:
pre[i][j]或pre[j][i]
- dis :二维数组,记录顶点 i 到顶点 j 的距离:
- 初始状态下,图的邻接矩阵如下和前驱顶点
- 第一轮循环中,以 A 作为中间顶点,将把 A 作为中间顶点的所有情况进行遍历,更新距离表和前驱关系
- C --> A --> G :路径长度为 9 ,顶点 B 和 G 的前驱结点为 A
- C --> A --> B :路径长度为 12 ,顶点 C 和 B 的前驱结点为 A
- G --> A --> B :路径长度为 7 ,顶点 G 和 B 的前驱结点为 A
- 第二轮循环中,以 B 作为中间顶点,将把 B 作为中间顶点的所有情况进行遍历,更新距离表和前驱关系
- 以此类推 … ,更换中间顶点,循环执行操作,直到所有顶点都作为中间顶点更新后,计算结束
- 为什么这样就能求出图中各个顶点到其他顶点的最短路径?这样来想,我们求出了每个顶点作为其他顶点的中间顶点的最短路径,那此时距离表中的路径值就是各个顶点到其他顶点的最短路径
# 9.5、弗洛伊德算法编码思路
- 由上述分析可知,需要三层 for 循环,所以弗洛伊德算法的时间复杂度为 O (n3)
for 顶点 A To 顶点 G { // 更换中间顶点
for 顶点 A To 顶点 G { // 更换起始顶点
for 顶点 A To 顶点 G { // 更换结束顶点
if(距离比上次更短){ //起始顶点到结束顶点距离比上次更短
更新距离表
更新前驱顶点表
}
}
}
}# 9.6、弗洛伊德算法代码实现
# 9.6.1、编写弗洛伊德算法
- 编写弗洛伊德算法
// 创建图
class Graph {
private char[] vertex; // 存放顶点的数组
private int[][] dis; // 保存,从各个顶点出发到其它顶点的距离,最后的结果,也是保留在该数组
private int[][] pre;// 保存到达目标顶点的前驱顶点
// 构造器
/**
*
* @param length 大小
* @param matrix 邻接矩阵
* @param vertex 顶点数组
*/
public Graph(int length, int[][] matrix, char[] vertex) {
this.vertex = vertex;
this.dis = matrix;
this.pre = new int[length][length];
// 对pre数组初始化, 注意存放的是前驱顶点的下标
for (int i = 0; i < length; i++) {
Arrays.fill(pre[i], i);
}
}
// 弗洛伊德算法, 比较容易理解,而且容易实现
public void floyd() {
int len = 0; // 变量保存距离
// 对中间顶点遍历, k 就是中间顶点的下标 ,[A, B, C, D, E, F, G] 走一遍
for (int k = 0; k < dis.length; k++) {
// 从i顶点开始出发,[A, B, C, D, E, F, G] 走一遍
for (int i = 0; i < dis.length; i++) {
// 到达j顶点,[A, B, C, D, E, F, G] 走一遍
for (int j = 0; j < dis.length; j++) {
len = dis[i][k] + dis[k][j];// => 求出从i 顶点出发,经过 k中间顶点,到达 j 顶点距离
if (len < dis[i][j]) {// 如果len小于 dis[i][j]
dis[i][j] = len;// 更新距离
pre[i][j] = pre[k][j];// 更新前驱顶点
}
}
}
}
}
// 显示pre数组和dis数组
public void show() {
for (int k = 0; k < dis.length; k++) {
// 先将pre数组输出的一行
for (int i = 0; i < dis.length; i++) {
System.out.print(vertex[pre[k][i]] + " ");
}
System.out.println();
// 输出dis数组的一行数据
for (int i = 0; i < dis.length; i++) {
System.out.print("(" + vertex[k] + "到" + vertex[i] + "的最短路径是" + dis[k][i] + ") ");
}
System.out.println();
System.out.println();
}
}
}# 9.6.2、测试代码
- 代码
public static void main(String[] args) {
// 测试看看图是否创建成功
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
// 创建邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;
matrix[0] = new int[] { 0, 5, 7, N, N, N, 2 };
matrix[1] = new int[] { 5, 0, N, 9, N, N, 3 };
matrix[2] = new int[] { 7, N, 0, N, 8, N, N };
matrix[3] = new int[] { N, 9, N, 0, N, 4, N };
matrix[4] = new int[] { N, N, 8, N, 0, 5, 4 };
matrix[5] = new int[] { N, N, N, 4, 5, 0, 6 };
matrix[6] = new int[] { 2, 3, N, N, 4, 6, 0 };
// 创建 Graph 对象
Graph graph = new Graph(vertex.length, matrix, vertex);
// 调用弗洛伊德算法
graph.floyd();
graph.show();
}- 程序运行结果
A A A F G G A
(A到A的最短路径是0) (A到B的最短路径是5) (A到C的最短路径是7) (A到D的最短路径是12) (A到E的最短路径是6) (A到F的最短路径是8) (A到G的最短路径是2)
B B A B G G B
(B到A的最短路径是5) (B到B的最短路径是0) (B到C的最短路径是12) (B到D的最短路径是9) (B到E的最短路径是7) (B到F的最短路径是9) (B到G的最短路径是3)
C A C F C E A
(C到A的最短路径是7) (C到B的最短路径是12) (C到C的最短路径是0) (C到D的最短路径是17) (C到E的最短路径是8) (C到F的最短路径是13) (C到G的最短路径是9)
G D E D F D F
(D到A的最短路径是12) (D到B的最短路径是9) (D到C的最短路径是17) (D到D的最短路径是0) (D到E的最短路径是9) (D到F的最短路径是4) (D到G的最短路径是10)
G G E F E E E
(E到A的最短路径是6) (E到B的最短路径是7) (E到C的最短路径是8) (E到D的最短路径是9) (E到E的最短路径是0) (E到F的最短路径是5) (E到G的最短路径是4)
G G E F F F F
(F到A的最短路径是8) (F到B的最短路径是9) (F到C的最短路径是13) (F到D的最短路径是4) (F到E的最短路径是5) (F到F的最短路径是0) (F到G的最短路径是6)
G G A F G G G
(G到A的最短路径是2) (G到B的最短路径是3) (G到C的最短路径是9) (G到D的最短路径是10) (G到E的最短路径是4) (G到F的最短路径是6) (G到G的最短路径是0) # 10、马踏棋盘算法
# 10.1、马踏棋盘游戏
- 马踏棋盘算法也被称为骑士周游问题
- 将马随机放在国际象棋的 8×8 棋盘
Board[0~7][0~7]的某个方格中,马按走棋规则 (马走日字) 进行移动。要求每个方格只进入一次,走遍棋盘上全部 64 个方格 - 游戏演示: http://www.4399.com/flash/146267_2.htm
# 10.2、马踏棋盘代码思路
- 马踏棋盘问题 (骑士周游问题) 实际上是图的深度优先搜索 (DFS) 的应用。为啥是图的深度优先搜索?
- 如果使用回溯(就是深度优先搜索)来解决,假如马儿踏了 53 个点,如图:走到了第 53 个,坐标 (1, 0),发现已经走到尽头,没办法,那就只能回退了,查看其他的路径,就在棋盘上不停的回溯……
- 可以使用前面的游戏来验证算法是否正确。
- 编码思路
- 创建棋盘 chessBoard,是一个二维数组
- 将当前位置设置为已经访问,然后根据当前位置,计算马儿还能走哪些位置,并放入到一个集合中 (ArrayList),下一步可选位置最多有 8 个位置, 每走一步,就使用 step+1
- 遍历 ArrayList 中存放的所有位置,看看哪个可以走通,如果走通,就继续,走不通,就回溯
- 判断马儿是否完成了任务,使用 step 和应该走的步数比较 , 如果没有达到数量,则表示没有完成任务,将整个棋盘置 0
- 注意:马儿不同的走法(策略),会得到不同的结果,效率也会有影响 (优化)
# 10.3、马踏棋盘代码实现
- 如下是马踏棋盘算法代码实现,在递归和回溯的过程中,如何判断马儿是否已经完成了任务?如下两个条件满足其一即可:
- 已经走够了步数
- 完成标志位 finished == true
- 如果回溯过程中,发现马儿并没有完成任务,则说明此次递归过程失败,应该棋盘该位置清零,并且标记当前位置并未被访问过
public class HorseChessboard {
private static int X; // 棋盘的列数
private static int Y; // 棋盘的行数
// 创建一个数组,标记棋盘的各个位置是否被访问过
private static boolean visited[];
// 使用一个属性,标记是否棋盘的所有位置都被访问
private static boolean finished; // 如果为true,表示成功
public static void main(String[] args) {
System.out.println("骑士周游算法,开始运行~~");
// 测试骑士周游算法是否正确
X = 8;
Y = 8;
int row = 1; // 马儿初始位置的行,从1开始编号
int column = 1; // 马儿初始位置的列,从1开始编号
// 创建棋盘
int[][] chessboard = new int[X][Y];
visited = new boolean[X * Y];// 初始值都是false
// 测试一下耗时
long start = System.currentTimeMillis();
traversalChessboard(chessboard, row - 1, column - 1, 1);
long end = System.currentTimeMillis();
System.out.println("共耗时: " + (end - start) + " 毫秒");
// 输出棋盘的最后情况
for (int[] rows : chessboard) {
for (int step : rows) {
System.out.print(step + "\t");
}
System.out.println();
}
}
/**
* 功能: 根据当前位置(Point对象),计算马儿还能走哪些位置(Point),并放入到一个集合中(ArrayList), 最多有8个位置
* @param curPoint
* @return
*/
public static ArrayList<Point> next(Point curPoint) {
// 创建一个ArrayList
ArrayList<Point> ps = new ArrayList<Point>();
// 创建一个Point
Point p1 = new Point();
// 表示马儿可以走5这个位置
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y - 1) >= 0) {
ps.add(new Point(p1));
}
// 判断马儿可以走6这个位置
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y - 2) >= 0) {
ps.add(new Point(p1));
}
// 判断马儿可以走7这个位置
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {
ps.add(new Point(p1));
}
// 判断马儿可以走0这个位置
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
ps.add(new Point(p1));
}
// 判断马儿可以走1这个位置
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
ps.add(new Point(p1));
}
// 判断马儿可以走2这个位置
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
ps.add(new Point(p1));
}
// 判断马儿可以走3这个位置
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
ps.add(new Point(p1));
}
// 判断马儿可以走4这个位置
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
ps.add(new Point(p1));
}
return ps;
}
/**
* 完成骑士周游问题的算法
* @param chessboard 棋盘
* @param row 马儿当前的位置的行 从0开始
* @param column 马儿当前的位置的列 从0开始
* @param step 是第几步 ,初始位置就是第1步
*/
public static void traversalChessboard(int[][] chessboard, int row, int column, int step) {
chessboard[row][column] = step;
//row = 4 X = 8 column = 4 = 4 * 8 + 4 = 36
visited[row * X + column] = true; //标记该位置已经访问
//获取当前位置可以走的下一个位置的集合
ArrayList<Point> ps = next(new Point(column, row));
//遍历 ps
while(!ps.isEmpty()) {
Point p = ps.remove(0);//取出下一个可以走的位置
//判断该点是否已经访问过
if(!visited[p.y * X + p.x]) {//说明还没有访问过
traversalChessboard(chessboard, p.y, p.x, step + 1);
}
}
//判断马儿是否完成了任务,使用 step 和应该走的步数比较 ,
//如果没有达到数量,则表示没有完成任务,将棋盘该位置设置为0
//说明: step < X * Y 成立的情况有两种
//1. 棋盘到目前位置,仍然没有走完
//2. 棋盘处于一个回溯过程
if(step < X * Y && !finished ) {
chessboard[row][column] = 0;
visited[row * X + column] = false;
} else {
finished = true;
}
}
}- 程序运行结果
骑士周游算法,开始运行~~
共耗时: 27099 毫秒
1 8 11 16 3 18 13 64
10 27 2 7 12 15 4 19
53 24 9 28 17 6 63 14
26 39 52 23 62 29 20 5
43 54 25 38 51 22 33 30
40 57 42 61 32 35 48 21
55 44 59 50 37 46 31 34
58 41 56 45 60 49 36 47 # 10.4、马踏棋盘代码优化
- 上面的算法那由于回溯过程过多,算法用时长,我们使用贪心算法(greedyalgorithm)进行优化。
- 马儿的下一步可能有很多种选择,我们应该怎么选择其下一步?
- 选择下一步的下一步走法尽可能少的,哈哈,我都给自己说晕了,这样尽可能减少递归的回溯,可明显提高算法速度
ArrayList<Point> ps = next(new Point(column, row));ps 是当前步骤的下一步走法的集合,我们需要对 ps 中所有的 Point 的下一步的所有集合的数目,进行非递减排序,就 ok 了
public class HorseChessboard {
private static int X; // 棋盘的列数
private static int Y; // 棋盘的行数
// 创建一个数组,标记棋盘的各个位置是否被访问过
private static boolean visited[];
// 使用一个属性,标记是否棋盘的所有位置都被访问
private static boolean finished; // 如果为true,表示成功
public static void main(String[] args) {
System.out.println("骑士周游算法,开始运行~~");
// 测试骑士周游算法是否正确
X = 8;
Y = 8;
int row = 1; // 马儿初始位置的行,从1开始编号
int column = 1; // 马儿初始位置的列,从1开始编号
// 创建棋盘
int[][] chessboard = new int[X][Y];
visited = new boolean[X * Y];// 初始值都是false
// 测试一下耗时
long start = System.currentTimeMillis();
traversalChessboard(chessboard, row - 1, column - 1, 1);
long end = System.currentTimeMillis();
System.out.println("共耗时: " + (end - start) + " 毫秒");
// 输出棋盘的最后情况
for (int[] rows : chessboard) {
for (int step : rows) {
System.out.print(step + "\t");
}
System.out.println();
}
}
/**
* 功能: 根据当前位置(Point对象),计算马儿还能走哪些位置(Point),并放入到一个集合中(ArrayList), 最多有8个位置
* @param curPoint
* @return
*/
public static ArrayList<Point> next(Point curPoint) {
// 创建一个ArrayList
ArrayList<Point> ps = new ArrayList<Point>();
// 创建一个Point
Point p1 = new Point();
// 表示马儿可以走5这个位置
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y - 1) >= 0) {
ps.add(new Point(p1));
}
// 判断马儿可以走6这个位置
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y - 2) >= 0) {
ps.add(new Point(p1));
}
// 判断马儿可以走7这个位置
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {
ps.add(new Point(p1));
}
// 判断马儿可以走0这个位置
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
ps.add(new Point(p1));
}
// 判断马儿可以走1这个位置
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
ps.add(new Point(p1));
}
// 判断马儿可以走2这个位置
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
ps.add(new Point(p1));
}
// 判断马儿可以走3这个位置
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
ps.add(new Point(p1));
}
// 判断马儿可以走4这个位置
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
ps.add(new Point(p1));
}
return ps;
}
/**
* 完成骑士周游问题的算法
* @param chessboard 棋盘
* @param row 马儿当前的位置的行 从0开始
* @param column 马儿当前的位置的列 从0开始
* @param step 是第几步 ,初始位置就是第1步
*/
public static void traversalChessboard(int[][] chessboard, int row, int column, int step) {
chessboard[row][column] = step;
//row = 4 X = 8 column = 4 = 4 * 8 + 4 = 36
visited[row * X + column] = true; //标记该位置已经访问
//获取当前位置可以走的下一个位置的集合
ArrayList<Point> ps = next(new Point(column, row));
//对ps进行排序,排序的规则就是对ps的所有的Point对象的下一步可走位置的数目,进行非递减排序
sort(ps);
//遍历 ps
while(!ps.isEmpty()) {
Point p = ps.remove(0);//取出下一个可以走的位置
//判断该点是否已经访问过
if(!visited[p.y * X + p.x]) {//说明还没有访问过
traversalChessboard(chessboard, p.y, p.x, step + 1);
}
}
//判断马儿是否完成了任务,使用 step 和应该走的步数比较 ,
//如果没有达到数量,则表示没有完成任务,将棋盘该位置设置为0
//说明: step < X * Y 成立的情况有两种
//1. 棋盘到目前位置,仍然没有走完
//2. 棋盘处于一个回溯过程
if(step < X * Y && !finished ) {
chessboard[row][column] = 0;
visited[row * X + column] = false;
} else {
finished = true;
}
}
//根据当前这个一步的所有的下一步的选择位置,进行非递减排序, 减少回溯的次数
public static void sort(ArrayList<Point> ps) {
ps.sort(new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
//获取到o1的下一步的所有位置个数
int count1 = next(o1).size();
//获取到o2的下一步的所有位置个数
int count2 = next(o2).size();
return count1 - count2;
}
});
}
}- 程序运行结果
骑士周游算法,开始运行~~
共耗时: 22 毫秒
1 16 37 32 3 18 47 22
38 31 2 17 48 21 4 19
15 36 49 54 33 64 23 46
30 39 60 35 50 53 20 5
61 14 55 52 63 34 45 24
40 29 62 59 56 51 6 9
13 58 27 42 11 8 25 44
28 41 12 57 26 43 10 7